基于频响函数识别结构非线性模态参数的方法

单卫东，臧朝平，张根辈，王平，邹亚晨，倪徳

(1.南京航空航天大学 能源与动力学院，江苏 南京 210016； 2.中国航发动力机械研究所，湖南 株洲 412002)

0 引言

模态分析理论和参数识别方法是模态参数识别的重要组成部分。由于准确、可靠地识别出结构的非线性模态参数难度较大，当前的模态分析和参数识别方法主要基于线性模型[1-2]，对于系统中的非线性常常忽略或者作为不确定性来处理。然而大多数的非线性结构并不能完全忽略其中的非线性，当作不确定性来处理也会带来很多误差。因此，建立一个准确、可靠的非线性模态参数识别方法是十分重要的。

非线性模态测试方法(nonlinear modal testing，NLMT)的研究在近年来取得了一定进展。臧朝平等[3-4]提出了分别用恒定位移幅值下的正弦激励识别非线性刚度参数和恒定速度幅值下的正弦激励来识别非线性阻尼参数的方法。CARRELLA等[5]提出了从测量的频响函数识别和量化工程结构中非线性的复频响函数法。

本文在文献[3-5]的基础上，提出在任意给定的速度响应幅值处，阻尼为常数，即将阻尼比描述成与速度幅值相关的参数，并引入加速度频响、速度频响、位移频响函数之间的转化关系，利用位移频响函数识别出与位移幅值相关的固有频率，利用速度频响函数识别出与速度幅值相关的阻尼比。通过非线性系统的仿真测试，验证该方法既能够检测出系统的刚度非线性，也能检测出阻尼非线性，且识别的非线性模态参数足够精确。

1 结构非线性模态参数辨识方法

1.1 非线性模态参数的线性等效

对于单自由度非线性系统，在受到简谐力的作用时，运动微分方程为：

(1)

通过步进正弦扫频信号激励后，可以将系统的位移频响函数定义为：

(2)

1.2 非线性模态固有频率识别

在任意给定的位移响应幅值处，存在一对点来定义相同的位移频响函数，如图1所示。如果不能直接测量得到位移幅值，可以通过位移频响函数乘以力来得到响应 ，即X(ω)=Hd×F。

图1 位移幅值线性化

在每个给定位移响应幅值下，可以通过一对对称的位移FRF点来定义位移频响函数的实部和虚部。

(3)

由式(3)可以得到与位移响应幅值相关的固有频率：

(4)

通过截取位移响应峰值两端对称的位移频响函数点，可以建立起固有频率与位移幅值、激励力幅值之间的对应关系：

ωr=f(X,F)

(5)

1.3 非线性模态阻尼比识别

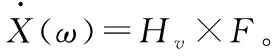
图2 速度幅值线性化

在每个给定速度响应幅值下，可以通过一对对称的速度FRF点来定义速度频响函数的实部和虚部。

(6)

由式(6)可以得到与速度幅值相关的模态损失因子：

(7)

其中模态损失因子是模态阻尼比2倍的关系ηr≈2ξ。

通过截取速度幅值两端对称的速度频响函数点，即可以建立起阻尼比与速度幅值、激励力幅值之间的对应关系：

(8)

2 非线性模态分析方法的仿真测试

2.1 非线性与线性系统的仿真验证

将上述方法分别应用于线性和非线性系统(同时包含刚度非线性项和阻尼非线性项)，对系统进行仿真分析来验证该方法的有效性。这里选用一个同时带立方刚度和平方阻尼的非线性单自由度系统，来与线性系统(其中knl=0，cnl=0)进行对比，其他仿真取值都一样,非线性系统的表达式如下：

(9)

在激励力幅值为0.2N、0.4N、1N时，线性系统与非线性系统的位移响应如图 3和图4所示。随着激励力幅值的增大，线性系统的位移响应峰值对应的频率不发生变化，而非线性系统的位移响应峰值对应的频率发生了明显的变化，即所谓的“频移”现象，这是非线性的表现。

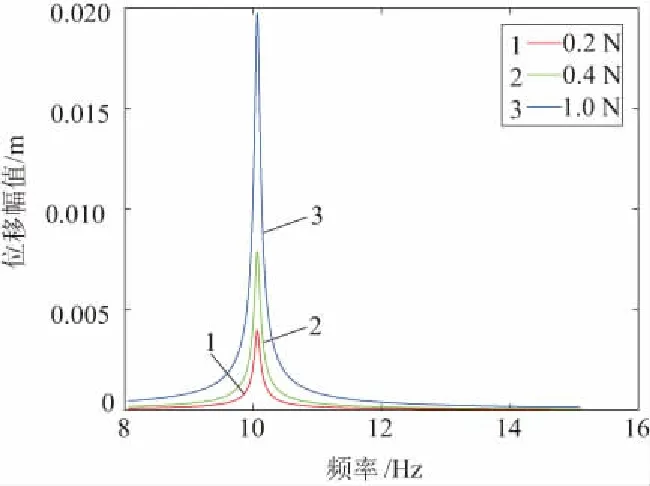
图3 线性系统位移响应

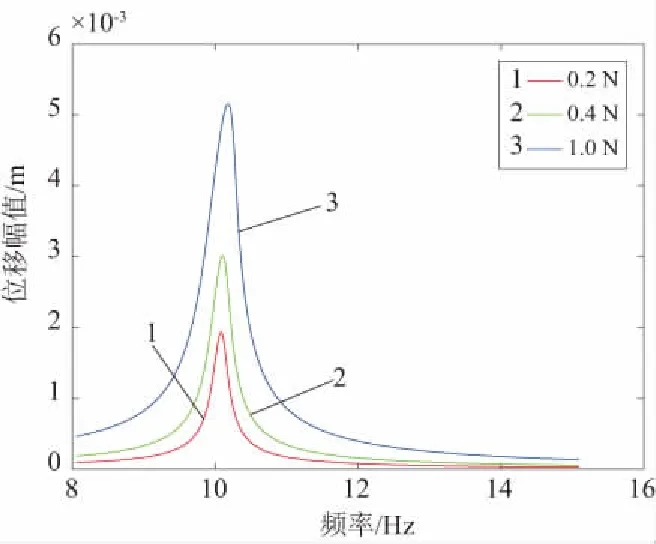
图4 非线性系统位移响应

对线性系统和非线性系统的位移频响函数进行分析，可以识别出非线性模态参数：与位移幅值相关的固有频率。如图5和图6所示，随着激励力幅值的增大，位移幅值逐渐增大，线性系统的固有频率随着位移幅值的增大保持不变，而非线性系统的固有频率随着位移幅值增大而增大。固有频率的变化反映出非线性系统包含的非线性刚度因素。

图5 线性系统固有频率随位移幅值的变化

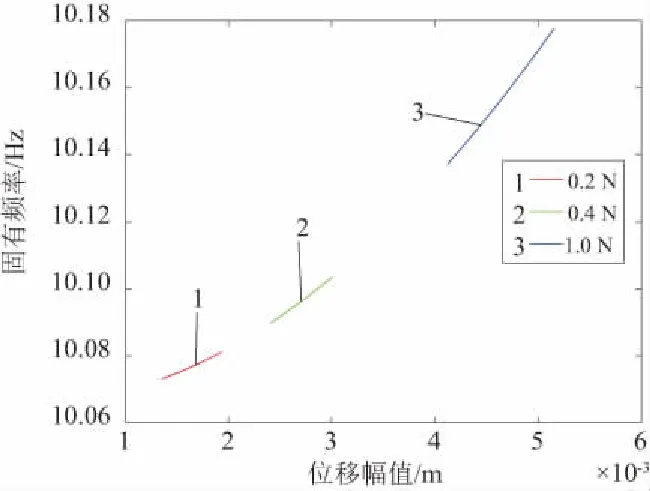
图6 非线性系统固有频率随位移幅值变化

对线性系统和非线性系统的速度频响函数进行分析，可以识别出非线性模态参数与速度幅值相关的阻尼比。如图7和图8所示，随着激励力幅值的增大，速度幅值逐渐增大，线性系统的阻尼比随着速度幅值的增大保持不变，而非线性系统的阻尼比随速度幅值的增大而增大。阻尼比的变化反映出非线性系统中包含的非线性阻尼因素。

图7 线性系统阻尼比随速度幅值的变化

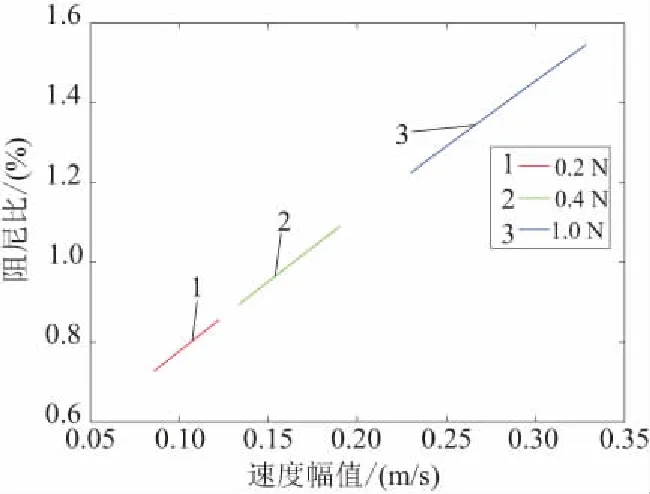
图8 非线性系统阻尼比随速度幅值的变化

2.2 非线性刚度函数的提取

将谐波平衡法应用到运动方程

(10)

求得等效刚度的表达式：

(11)

式中X是响应的幅值。通过式(3)可以发现等效刚度是从一个恒定值(底层线性系统)开始，与位移幅值2次方的关系开始增加。通过上面非线性模态识别方法，基于仿真分析得到位移频响函数，可以提取得到系统固有频率随位移幅值的变化，求得非线性等效刚度的表达式：

(12)

如图9所示，在激励幅值为1N时，通过非线性模态参数识别方法(CFRF)提取的等效刚度函数与谐波平衡法(HBM)的对比，误差不超过0.5%。因此，本方法能精确地识别出非线性系统的刚度函数。

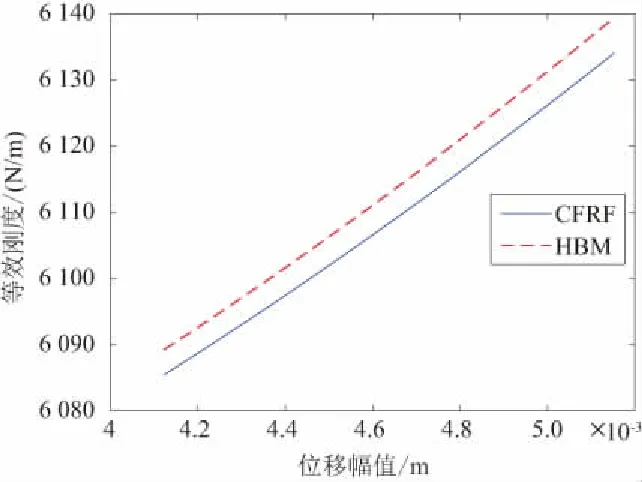
图9 仿真提取刚度函数与谐波平衡法的对比

2.3 非线性阻尼函数的提取

类似地，将谐波平衡法应用到运动方程：

(13)

求得等效阻尼的表达式：

(14)

稳态速度响应的幅值近似为：

V=ωX

(15)

则有：

(16)

通过上式可以发现等效阻尼与速度幅值呈线性的关系。通过上面非线性模态识别方法，基于仿真分析得到速度频响函数，可以提取得到系统阻尼比随速度幅值的变化，求得非线性等效阻尼的表达式：

(17)

如图10所示，在激励幅值为1N时，通过CFRF提取的等效阻尼函数与HBM的对比，误差不超过1%。因此，本方法能准确地识别出非线性系统的阻尼函数。

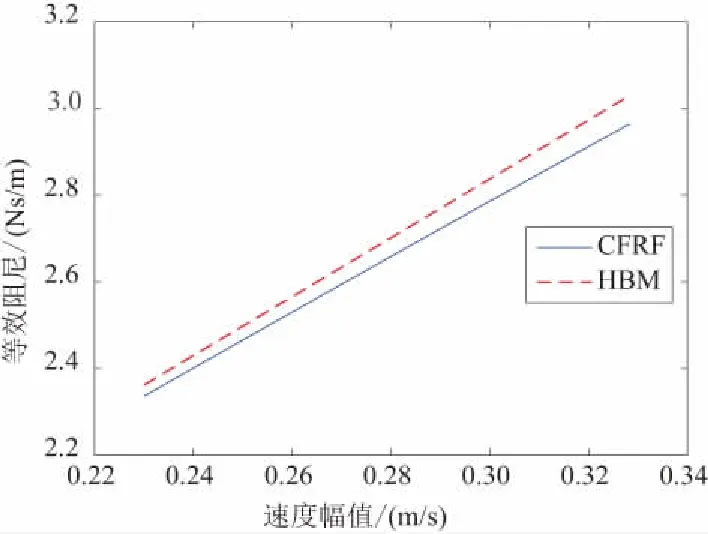
图10 仿真提取阻尼函数与谐波平衡法的对比

3 结语

本文提出了基于频响函数识别结构非线性模态参数的方法。主要得到以下结论：

1) 基于等效线性化理论，通过标准的模态试验，可以识别和量化系统的非线性模态参数，具有重要的工程实用价值。

2) 通过非线性系统与线性系统的仿真对比，验证该方法既可以检测系统的刚度非线性，也可检测阻尼非线性。

3) 通过非线性模态参数提取的非线性等效刚度和阻尼函数，与谐波平衡法的结果误差均在1%以内，验证了该方法识别非线性模态参数的精确性。