基于三次样条曲线插值的传感器温度补偿

李淮江，王冰冰

（淮北师范大学 物理与电子信息学院，安徽 淮北 235000）

精密测量技术作为推动国民经济发展的重要基础技术之一，已成为先进制造业中极其重要的组成部分。现阶段，固定环境温度下的压力测量问题已经能够得到很好的测量结果，各种类型的测量设备和测量的方法也日趋完善[1-2]。随着国民经济的发展，诸如气象测试、武器装备、地质勘探、航空航天等领域对传感器在大幅温度变化范围内的测量精度以及测试稳定性提出了越来越高的要求，测量设备使用传统的方法往往不能达到所需的准确性和稳定性，在这样的背景下，诸多学者以提高现有传感器的测量精度和稳定性为目的，提出了许多创新性的补偿方法。一个完善的温度补偿系统对于压阻式压力传感器温补偿的研究具有十分重要的理论意义和实用价值。

1 软件补偿方法

软件补偿技术实现相对简单，补偿效果明显，是提高压力传感器精度的重要途径[3]。所以，在现代流行的压力传感器温度补偿中大都采用软件补偿。目前的软件补偿方法主要采用分段线性插值法、神经网络方法和三次样条曲线插值的方法。也有不少学者通过结合多种温度补偿算法来达到高精度温度补偿的目的，例如传统回归算法和遗传算法的结合，在传感器的温度补偿实验中取得了良好的效果[4]。其中，神经网络算法存在网络结构选择不一、训练时间过长等问题，而综合算法需要长期的实践经验为基础，两者都没有得到广泛的推广应用。目前比较流行的温度补偿方法有分段线性插值法和三次样条曲线插值法。

1.1 分段线性插值法

分段线性插值法的基本思想是将传感器的输入信号区间分割成若干个小区间，然后根据各个小区间内的标定数据，将传感器的输出信号拟合为以输入信号为自变量的直线，以这条直线段代表传感器的实际静态特性曲线[5]。具体拟合直线如图1所示。

分段线性插值法很少被应用到高精度的传感器温度补偿当中，因为实际的传感器输出信号是一条光滑的曲线，而分段线性插值的思想是利用直线代替曲线，在现有的拟合直线算法当中，无论如何都会造成两者之间的误差。虽然理论上来说只要分段足够多，拟合直线就能无限接近实际的传感器静态特性曲线，但计算量也将随之增大；并且由于是分段直线拟合，在各插值节点处相邻线段不能保证良好的光滑性，并不能够准确的表达传感器静态特性，所以在高精度测量中很少使用。

图1 分段线性插值法拟合曲线

1.2 三次样条曲线插值算法

三次样条曲线插值的方法是目前使用较为广泛的一种方法，它是由一段段连续的三次多项式连接而成，在连接点处一阶、二阶可导，且导数连续，具有良好的光滑性，能够准确反应传感器的真实特性[6]。

假设一个在区间[a,b]上二次连续可微的函数f(x)，在区间[a,b]上选定n+1个插值节点并且：a=x1＜x2＜…＜xn+1=b。设函数

若S(x)同时满足下列条件：

(1)S(x)在每个小区间上最高次幂都是不大于3，i+1,2，…，n+1；

(2)S(x)在每个小区间上都具有二阶导数且导数连续；

则称S(x)是函数f(x)的3次样条插值函数。

设mi=S"(xj)，hi=xi+1-xi，由于S(x)的二阶导数在每一个子区间上都是连续的，于是在区间[xi，xi+1]上

对(3)式连续积分两次：

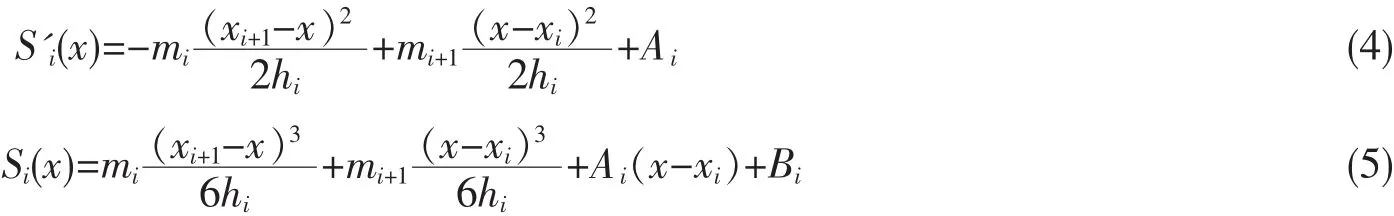
式中 Ai，Bi为积分常数，由（1）、（5）得

将（6）式代入（4）式得

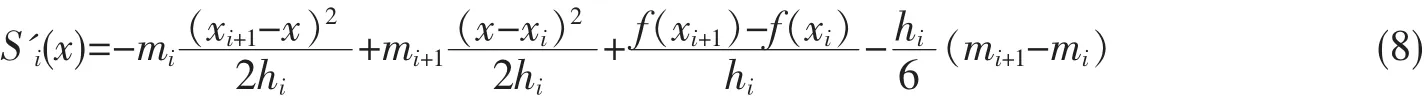
由于 S′i(x)连续，在相邻区间[xi-1，xi]和[xi，xi+1]上的公共点 xi处有相同值，即

由（9）式得

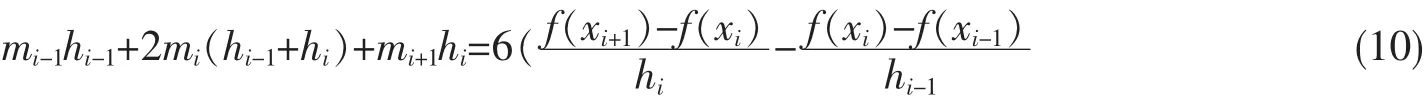
结合边界条件：

得到 n-2 个方程组，求解得到 m1，m2，...，mn的值，对mi连续两次积分求得三次样条插值函数在各小区间对应的子函数S(xi)[7-8]。

图2为三次样条曲线插值法拟合的曲线，通过对比图1所示的分段线性插值拟合的传感器特性曲线，从两条拟合曲线的比较可以看出：三次样条插值曲线更能够符合实际传感器传递特性。

图2 三次样条曲线插值法拟合曲线

2 实验数据分析与处理

实验选用BS10系列绝压传感器为研究对象，18B20温度传感器检测系统环境温度，采用高精度的16位AD转换器AD7705对传感器输出信号进行采集和转换，配合控制单元STC89C58构成数据采集系统对传感器的输出信号进行分析和验证。数据采集系统实物图如图3所示。

温度补偿实验开始前需要对传感器进行全温度范围内的静态特性标定，温度标定范围：-20℃～+60℃。在每个标定的温度点施加标准压力，压力标定范围：1014.0～3014.0hPa，测得补偿前传感器输出数据如表1所示，得到99个标定数值[9]。

由标定数据可以看到，在同一标定压力下，传感器输出数据随着温度的升高而减小，说明传感器发生了温度漂移，为了保证其应用范围，必须进行温度补偿。

图3 采集系统实物图

下面举例说明三次样条曲线插值的具体补偿步骤。例如，环境温度为8℃，传感器输入压力为1514.0 hPa，以传感器输出数值来说明二维插值过程。输入压力为1514.0 hPa时，对应固定温度下各条特性曲线的第三个区间[1414.0，1614.0]。所以，先求出不同温度时的各条特性曲线的第三小区间[1414.0，1614.0]的三次样条系数。而后，将1514.0 hPa代入这些小区间的三次样条系数求出在不同温度时此压力下所对应的传感器输出数值，如表2所示。

最后，对所得不同温度下P=1514.0 hPa时传感器的输出数值和各温度点进行三次样条插值，得到各温度区间下P=1514.0hPa时的传感器输出数值的函数关系式，各温度区间的三次样条多项式系数如表3所示。

表1 补偿前传感器静态输出数据

表2 各温度点在第三小区间的三次样条系数及对应结果

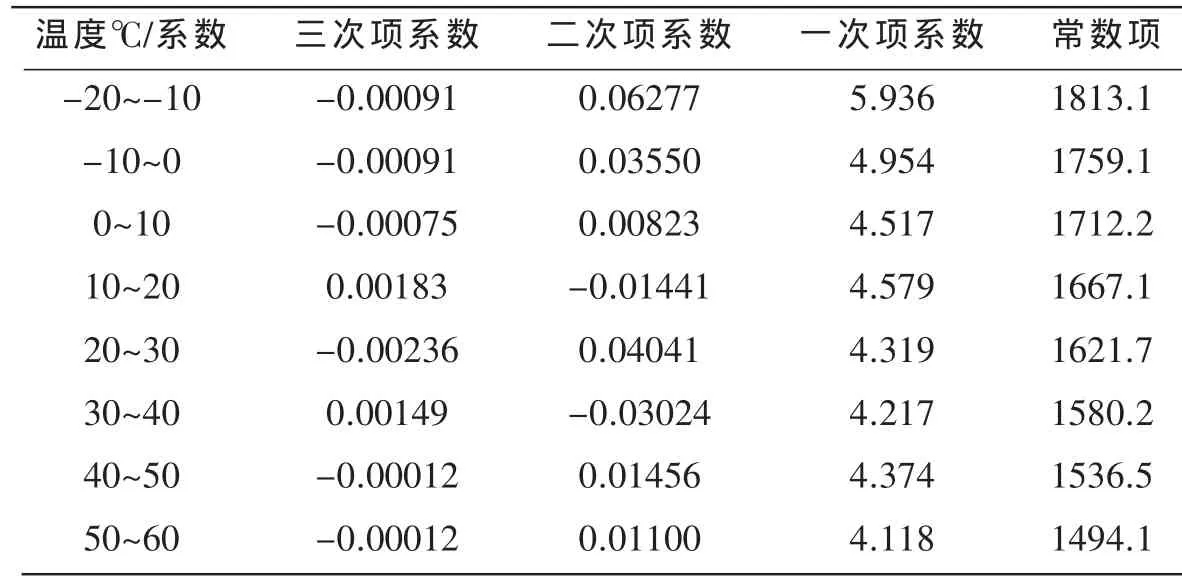
表3 计算结果对温度三次样条插值后各区间系数

将t=8℃代入区间 [0，10]所对应的三次样条插值函数即可求出此时的传感器输出数值。 -0.00075×（8-0）3+0.00823×（8-0）2-4.517×（8-0）+1712.2=1676.2。 这样就建立了标定温度、标定压力和传感器输出数值的一一对应关系，如果未补偿时传感器的输出数据是1676.2 hPa，则经过补偿后传感器的输出数据应该为此时的标准压力1514.0 hPa。

3 误差分析

分段线性插值法的补偿方法与三次样条曲线插值的补偿方法基本相同，只是将三次样条的曲线拟合为只有一次项的直线，由于这种方法是利用直线段来代表传感器的实际特性曲线，所以在实际的操作过程中难免造成较大误差[5]。

进行温度补偿后的传感器在各插值节点处的误差理论上来说会是零，为了正确的检测温度补偿后传感器的性能指标，选取各插值节点的中点作为检测传感器性能的检测点[10]，是利用分段线性插值法和三次样条曲线插值法两种补偿方法后的传感器输出数据在各检测点的误差分布见图4。

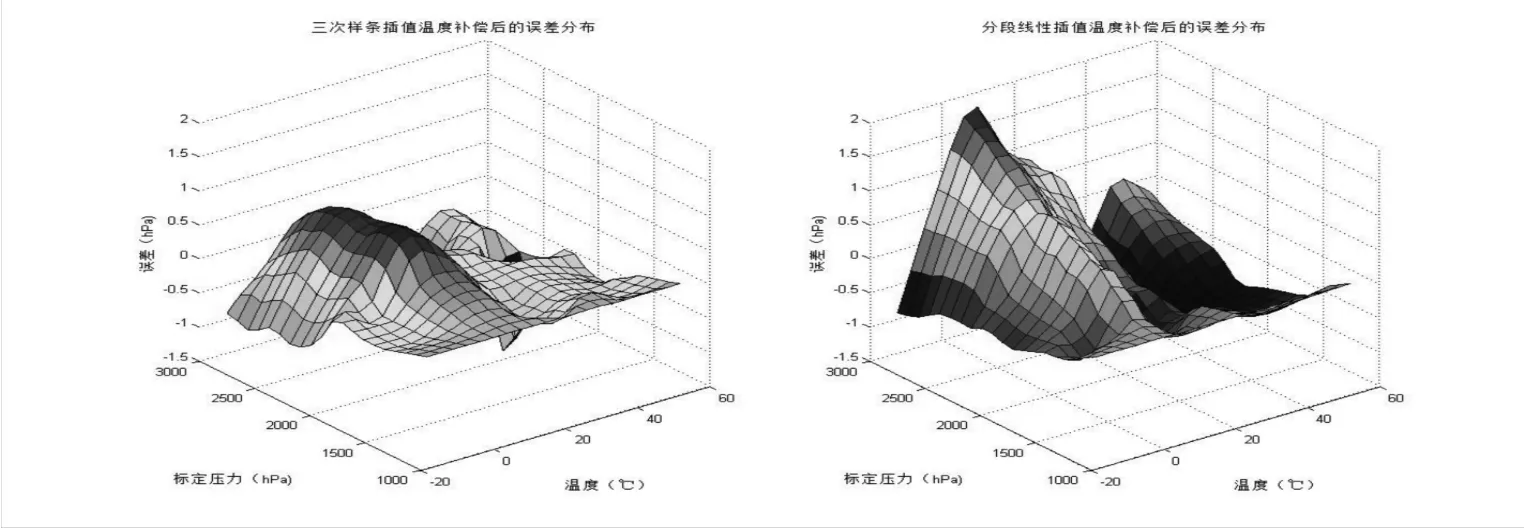
图4 两种温度补偿后的传感器误差分布

分段线性插值法进行传感器温度补偿后的，其最大误差分布在5℃、2914.0 hPa处，最大误差1.9hPa，对应传感器精度0.095%;三次样条插值法对传感器进行温度补偿后，最大误差分布在-15℃、2714.0 hPa处，最大误差0.9 hPa，对应传感器精度0.045%。

4 结论

介绍了基于三次样条曲线插值算法的传感器温度补偿方法，并且结合了全温度范围内的传感器标定数据详细的阐明了三次样条曲线插值法的具体操作步骤，实现了传感器在全温度范围内的高精度补偿，这在国内已有的文章中并不多见。同时对比了分段线性插值法温度补偿后的传感器误差分布情况，证实了三次样条曲线插值算法的有效性。该方法对于其他的数据采集系统精度的提升有一定的借鉴意义。

［1］胡帆，陈正一.PTB220 系列数字式气压表的原理与应用［J］.气象水文海洋仪器，2008，2：64－67.

［2］张伟星，王晓蕾，陈晓颖，等.电子探空仪气压传感器特性［J］.解放军理工大学学报：自然科学版，2001，12（6）：696－701.

［3］杨雪，刘诗斌.压力传感器温度补偿各种算法的比较分析［J］.电子设计工程，2013，21（10）：90－92.

［4］陈晓颖，宋爱国，李建清，等.遗传算法在硅压阻气压传感器温度补偿中的应用［J］.测控技术，2010，29（S）：305－308.

［5］赵航，张大力.高温环境下压力传感器的温度补偿方法研究［J］.仪器仪表装置，2012，27（8）：18－21.

［6］李新.三次样条插值在称重仪表误差补偿中的应用［J］.电子设计工程， 2011（11）：48－51.

［7］林成森.数值计算方法［M］.北京：科学出版社，1998：152－167.

［8］WANG XIAOJIA， YANG SHANLIN.Dynamic GM （1，1） Model based on cubic spline for electricity consumption prediction in smart grid［J］.China Communications， 2010（10）：83－88.

［9］何伟铭，蒋超伟，井原透.高精度传感器标定曲线的预测拟合［J］.传感技术学报，2013，26（11）：1519－1524.

［10］高磊，马英辉，刘祎，等.高精度硅压阻式气压计设计［J］.工矿自动化，2013，39（12）：21－25.