Timoshenko梁静力学和动力学问题有限体积法求解

井丽龙,张文平,明平剑,付丽荣,刘晓刚

(哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)

Timoshenko梁静力学和动力学问题有限体积法求解

井丽龙,张文平,明平剑,付丽荣,刘晓刚

(哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)

为探究Timoshenko梁模型数值计算方法，开展了基于有限体积法的Timoshenko梁数值计算方法研究。利用有限体积法对考虑剪切变形的梁进行了离散，并进行了静力学分析和动力学分析，通过几个经典算例将此方法所得到的数值解与解析解及有限元解进行了对比，结果证明，有限体积法有较高精度。与此同时利用有限体积法离散Timoshenko梁时当梁为细长梁时不存在剪切自锁现象。有限体积法可以应用于Timoshenko梁模型静力弯曲分析、固有特性和动力响应分析。

有限体积法；Timoshenko梁；静力学；动力学；剪切自锁现象; 固有频率；位移响应

在有限元结构分析中，深梁和中厚板剪切自锁是比较突出的问题，它通常给出较大误差的结果来掩盖真实的求解值。如果不仔细对结果进行分析，带来的后果是十分严重的。尤其是对于应用广泛的梁、板、壳体结构，弯曲变形是主要变形形式，不合理的剪切自锁将带来巨大误差的分析结果。做任何复杂的工程分析前，有必要对自锁问题进行分析。有限元方法中常采用减缩积分单元、全积分二阶单元、一阶单元细密格式和Wilson非协调模式[1]来解决此问题且相对复杂，而有限体积法却有着独特的性质即对于Timoshenko梁模型在分析细长梁时不存在剪切自锁现象，其原因是有限体积法所列的方程来自于对各控制体广义力平衡方程，计算中没有有限元法中数值积分这一过程，因此不存在有限元中出现的剪切自锁现象，进而有必要研究基于有限体积法对Timoshenko梁在不同跨高比下的静力学与动力学研究。有限体积法作为一种数值计算的方法多应用于流体、传热等领域[2-6]，其在结构计算方面的应用较少。Demirdzic等采用有限体积法，在处理固体力学离散单元间位移分布时，提出了将一个单元与周围单元位移采用线性分布，通过用常应变平面单元平均分配两个单元之间的位移计算出应变，并奠定了有限体积法应用于结构分析的基础。Wheel采用单元与每个面单元间位移线性分布假设，并对Mindlin板进行了分析，其结果认为采用中厚板模型模拟薄板时没有“自锁现象”。在用有限元法对大跨高比Timoshenko梁模型分析时会出现剪切自锁现象，即梁过度刚硬不发生弯曲变形只有零解，这是由于约束条件未能精确满足，在梁很薄时导致不确定地夸大了剪切应变能项的量级而造成的，在梁、板、壳的有限元分析中，此种现象称为剪切自锁现象，而利用有限体积法解决考虑剪切变形的梁、板模型时却不存在剪切自锁现象[7-8]。

本文利用有限体积法基于Timoshenko梁模型对不同跨高比的梁进行了静力分析[8]，固有频率提取和动力响应分析验证了有限体积法能够对Timoshenko梁模型进行较精确的模拟并展现出此方法不存在剪切自锁的现象。

1 控制方程

1.1 平衡方程

(1)

式中:σ是应力张量，F是体力向量，u是位移向量。当问题为静力问题时惯性力为零。

1.2 本构方程

Timoshenko梁理论源自1921年Timoshenko提出的及剪切变形的梁修正理论，在分析中将剪切变形和转动惯量考虑进去。Timoshenko梁模型适合于描述短梁、层合梁受高频激励所引起的振动现象。

由材料力学的基本公式可知：

(2)

式中：M、Q为弯矩和剪力，E为杨氏模量，I为截面惯性矩，ψ为弯矩引起的转角，w为挠度，k'为剪切修正系数(矩形截面时取0.833)[9]，A为截面面积，G为剪切弹性模量。

2 数值方法

对于Timoshenko梁模型，此模型为一维模型，对于梁的状态用两个变量(挠度w和截面转角ψ)描述。对于此一维模型本文采取的是均匀网格来进行计算，如果要进行非均匀一维网格的相关计算可引入等参单元再进行相应计算。

本文采用的是两节点一维控制体对梁模型进行离散，基于有限体积法中的格心法将两个变量(挠度w和截面转角ψ)存储于控制体中心，控制体之

间界面的值可通过相邻两个控制体中心变量的插值得到。控制体离散示意图如下图1所示。取其中一个控制体，其受力如图2所示。

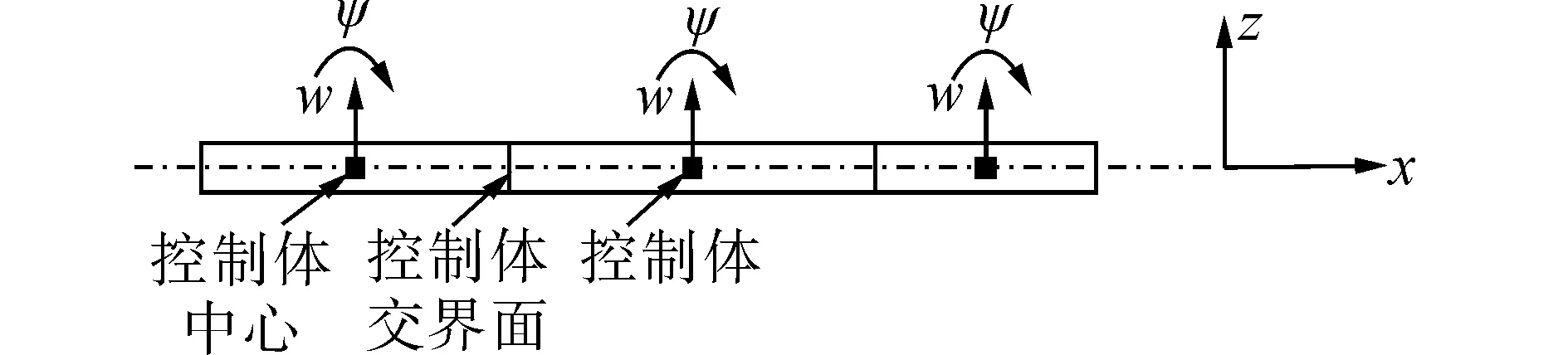
图1 控制体离散示意图Fig. 1 Discrete control volume

图2 控制体受力示意图Fig. 2 A control volume under internal and external loads

其广义力平衡方程为

(3)

式中：n为法向方向(+1或者-1)，Mc、Jc分别为单元质量和转动惯量，M、Q分别是弯矩、剪力，q为均布载荷，Fp为集中载荷，由于小变形假设cosθi=1。

将方程(2)代入式(3)，可得到关于挠度w和截面转角ψ为未知量的方程组：

(4)

对于方程中的dψ/dx和dw/dx项采用线性插值的方法进行近似。

图3 控制体变量示意图Fig. 3 Variable of the control volume

假设i为第i个节点，则角标i表示各节点变量，假设ic表示第i个控制体中心变量，如图3所示，则根据线性插值可以得到

(5)

边界控制体处理：

左边界控制体

(6)

右边界控制体

(7)

对于边界条件处理：两端简支，w1=0,M1=0,wn+1=0,Mn+1=0；两端固支，w1=0,ψ1=0,wn+1=0,ψn+1=0；一端固支一端自由，固支端采用与上式相同式子，自由端Mn+1=0,Qn+1=0推导出广义位移的关系。

通过对所有离散单元列平衡方程可以得到求解梁方程的一般矩阵形式，其压缩形式如下：

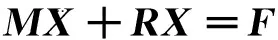
(8)

2.1 静力学分析

对于静力学问题，其中一个控制体其广义力平衡方程与式(3)类似，令惯性力为零即可得到

RX=F

(9)

式中：R为2n×2n对称带状矩阵，与几何参数材料参数有关；X为广义位移(各控制体中心的挠度与转角)；F为广义载荷(等效的力与弯矩，通过力平衡将其等效)，线性方程组的求解采用一般的数值解法即可实现如高斯消去法。

2.2 固有频率提取

对于Timoshenko梁模型，其自由振动方程为式(8)去掉外载荷项。由梁的理论可假设位移响应满足如下关系：

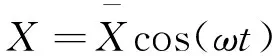
(10)

则可推导出频率方程：

(11)

利用QR分解法可求得相应的特征值，开平方即为相应的固有频率。

2.3 动力响应分析

当梁受到外部激励时，它将产生动力响应，由于弹性体的振型具有正交性，因此可以用模态分析法，方便地求得弹性体对外部激励的响应，当用有限体积法进行近似时主要基于以下思路：

1) 应用达朗贝尔原理对每个离散后的控制体建立广义力平衡方程：∑Mc=0,∑Fz=0。

2) 集成所有控制体形成整个梁的广义力平衡方程进而形成振动方程，形式如式(8),此式左边各项见固有频率分析，F代表外部受到的激励f(x,t)。

3) 对相应时间项x(x,t)的求解采用经典的中心差分法[9]进行求解。

3 算例

3.1 悬臂梁受均布载荷静力分析

均布载荷Q=100 N/m;梁长L=1 m;梁宽T=0.02 m；梁高为H;剪切修正系数Ks=0.833; 杨氏模量E=210 GPa;泊松比0.3。

悬臂梁挠度曲线表达式[10]：

(12)

式中:α为剪切系数[10]。计算了3种跨高比的挠度：选择梁截面高度为0.008m，宽度为0.02m，跨高比为125，计算结果如图5(a)。其次选择梁截面高度为0.02m，宽度为0.02m，跨高比为50，计算结果如图5(b)。最后选择梁截面高度为0.2m，宽度为0.01m，跨高比为5，计算结果如图5(c)。

图4 悬臂梁示意图Fig. 4 Cantilever beam under equal distributing loads

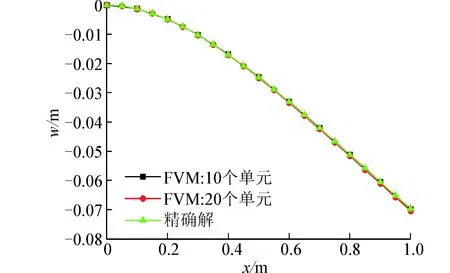
(a) L/H=125

(b) L/H=50

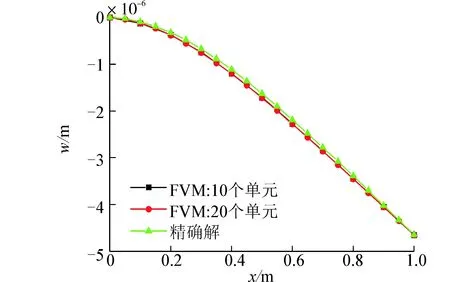
(c) L/H=5图5 悬臂梁受均布载荷挠度曲线Fig. 5 The deflection curve for different L/H cantilever beams under uniform load

通过计算3种跨高比悬臂梁的挠度，从结果可以看出随着离散控制体数的增加用有限体积法计算的结果趋近于精确解，并且当跨高比大于100时Timoshenko梁模型不存在剪切自锁现象。

3.2 简支梁受均布载荷静力分析

均布载荷q=1 000 N/m;梁长L=1 m;梁宽T=0.02 m;梁高为H;剪切修正系数Ks=0.833; 杨氏模量E=210 GPa;泊松比为0.3;铁木辛柯梁模型精确解：

(13)

式中：α为剪切修正系数，具体推导见文献[11]。

图6 简支梁示意图
Fig. 6 Sketch of simply-supported beam

计算了3种跨高比的挠度以及与精确解的误差：首先选择梁截面高度为0.2m，宽度为0.02m，跨高比为5，计算结果如图7(a)，其次选择梁截面高度为0.02m，宽度为0.02m，跨高比为50，计算结果如图7(b)，最后选择梁截面高度为0.008m，宽度为0.02m，跨高比为125，计算结果如图7(c)。

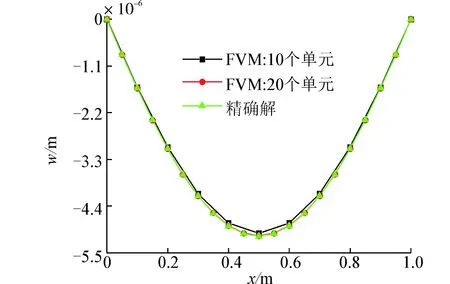
(a) L/H=5

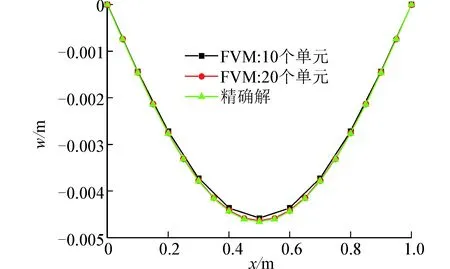
(b) L/H=50

(c) L/H=125图7 简支梁受均布载荷挠度曲线Fig. 7 The deflection curve for different L/Hsimply-supported beams under uniform load

将上述3种跨高比的数值结果进行误差分析，其误差如图8所示:

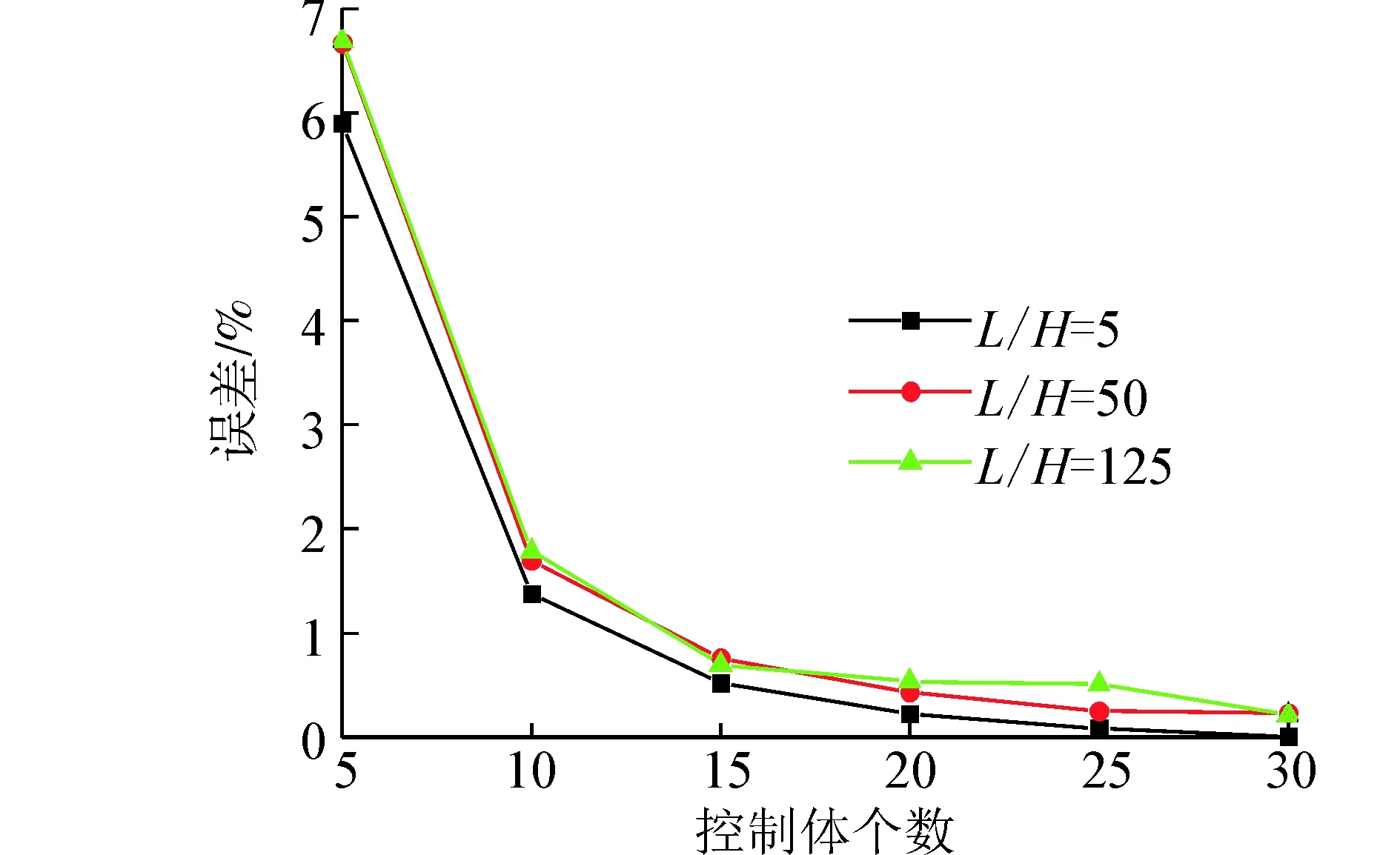
图8 不同跨高比数值解与精确解的误差Fig. 8 Error in the numerical and exact solution in different length-height ratios

此算例计算了3种跨高比简支梁的挠度并与精确解进行了对比和相对误差的计算，通过分析可知此方法对于不同跨高比的简支梁同样能够较精确的描述并且随着离散控制体的增加其得到的数值解与精确解的误差在逐渐降低，与此同时当跨高比大于100时不存在剪切自锁现象,进而也验证了有限体积法可以应用于梁的静力分析。

3.3 简支梁固有频率的提取

简支梁如图6所示，梁长度为1m;材料密度为7 800kg/m3；材料泊松比为0.3。固有频率精确解[11]为

r=1，2,3...

(14)

计算了两种跨高比简支梁的固有频率，分别对有限体积法及有限元法进行了误差分析：首先用有限体积法和有限元法分别计算了截面高度为0.01m、宽度为0.01m，即跨高比为100的简支梁的前三阶固有频率，并与精确解进行了对比如图9(a)，其次用有限体积法和有限元法分别计算了截面高度为0.1m，宽度为0.01m即跨高比为10的简支梁的前三阶固有频率，并与精确解进行了对比如图9(b)。

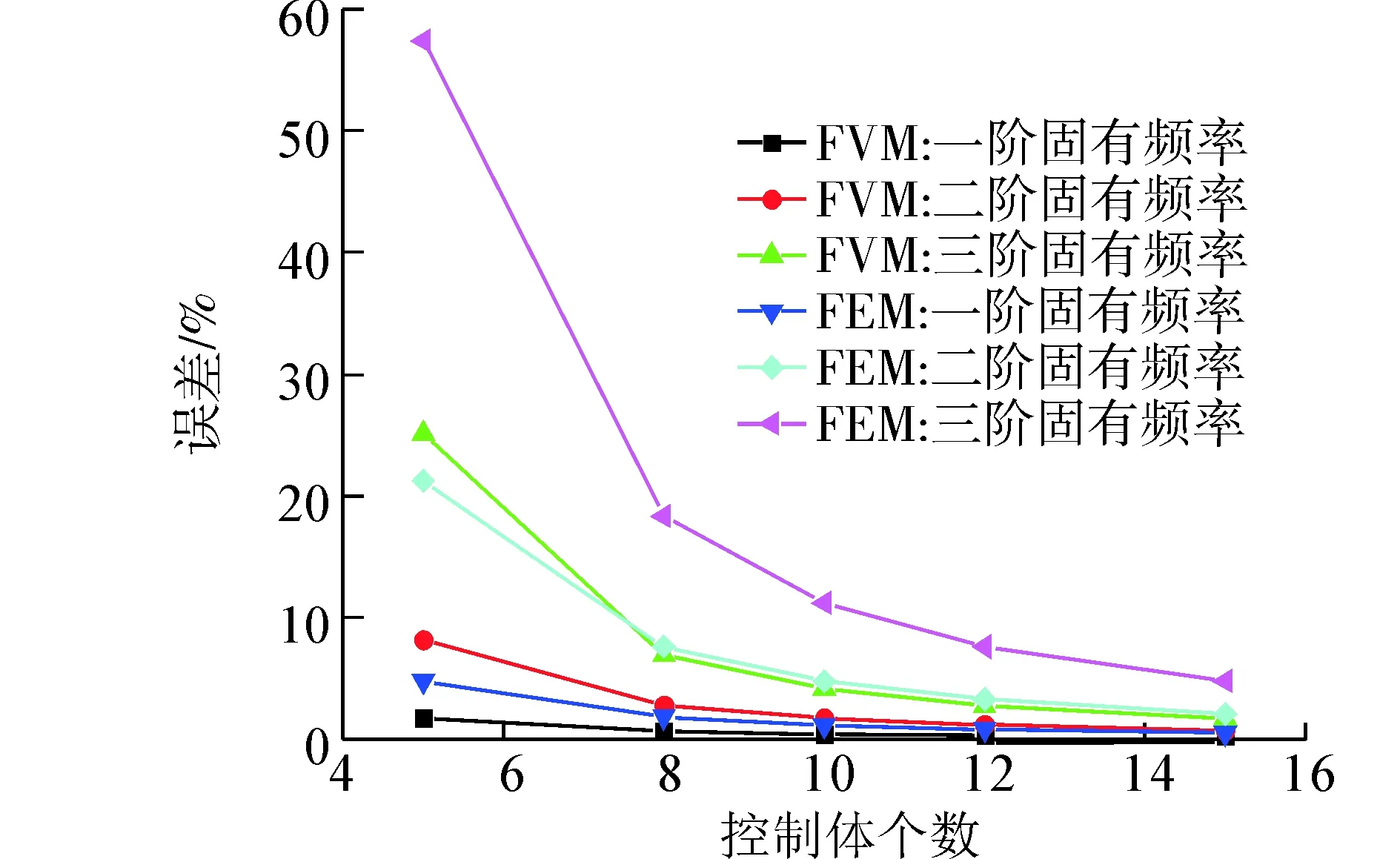
(a) L/H=100

(b) L/H=10图9 简支梁前三阶固有频率误差分析Fig. 9 Error analysis of first, second and third natural frequencies for simply-supported beam

此算例计算了2种高跨比梁的前三阶固有频率，通过以上两图对比可以看出随着控制体数的增加固有频率与精确解的误差是越来越小的，与此同时在相同离散单元的情况下，对于前三阶固有频率的提取有限体积法的精度要比有限元的精度高。并且利用有限体积法得到的一阶固有频率与精确解之间的误差最小，因此用有限体积法离散并用相应提取特征值技术进行计算所得到的固有频率是相对准确的，进而验证了有限体积法可以应用于Timoshenko梁模型固有频率的提取。

3.4 简支梁动力响应分析

3.4.1 算例1

简支梁如图6所示，所承受载荷为Q，其随时间分布如图10所示;材料密度为7 800 kg/m3；泊松比为0.3；杨氏模量为210 GPa；剪切修正系数取0.833,选取的时间步长为10-6s，计算3种不同跨高比的梁中点响应。

图10 载荷随时间分布图(均布载荷)Fig. 10 Load-time curve(uniform load)

根据此载荷分布则解析解[12]：

当t<0.001s时，

(i=1,2,3,4)

(15)

当t>0.001 s时，

(i=1,2,3,4)

(16)

(a) L/H=5

(b) L/H=20

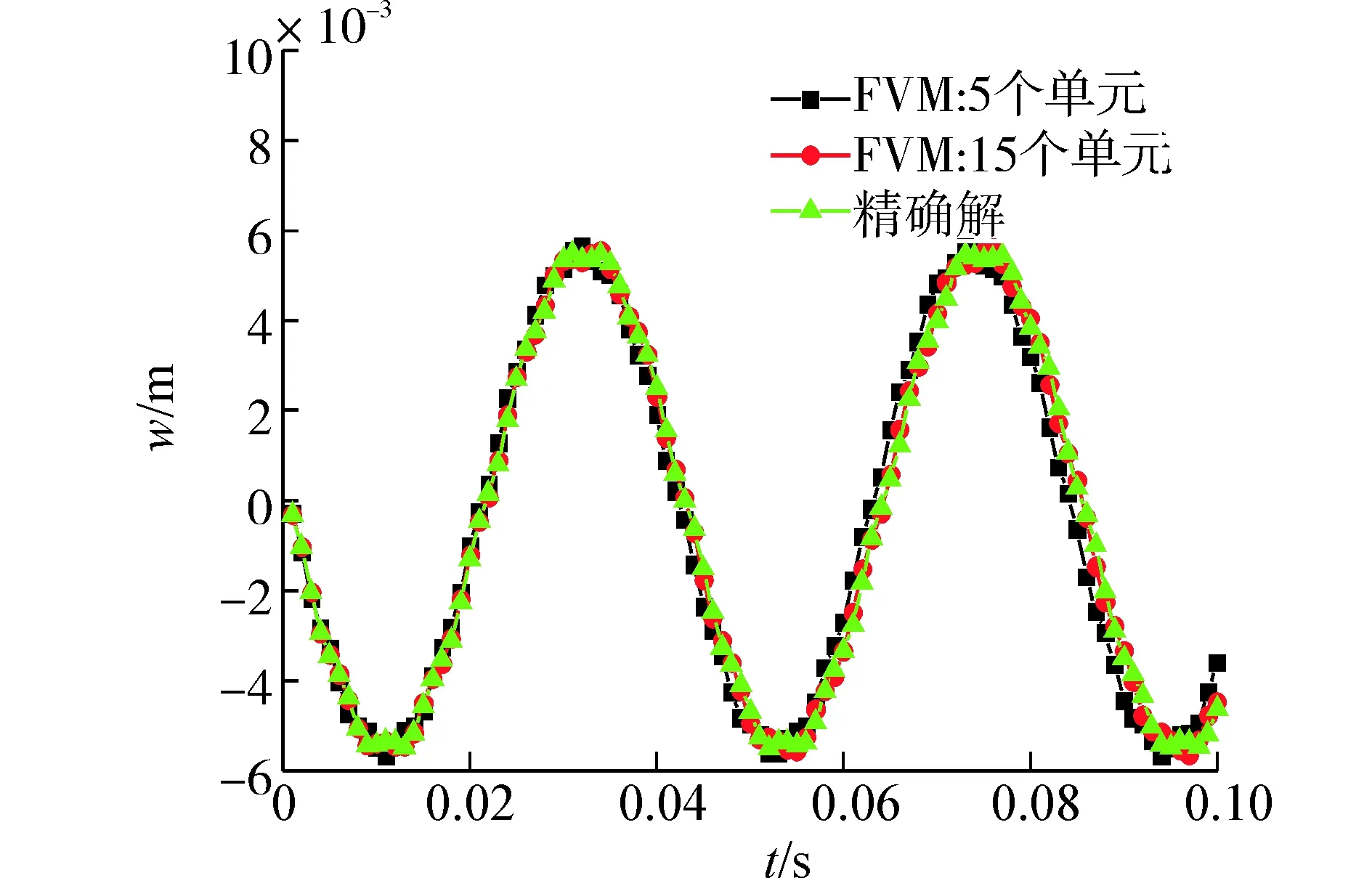
(c) L/H=100图11 简支梁受均布载荷位移响应曲线Fig. 11 Displacement-time curve for simply-supported beam under uniform load

首先计算了截面高度为0.2 m、宽度为0.01 m即跨高比为5，载荷分布如图10，0.005 s的梁中点位移响应，结果如图11(a)，然后计算了截面高度为0.05 m、宽度为0.02 m即跨高比为20，载荷分布如图10，0.02 s的梁中点位移响应，结果如图11(b)，最后计算了截面高度为0.01 m、宽度为0.02 m即跨高比为100，载荷分布如图10，0.02 s的梁中点位移响应，结果如图11(c)。

此算例计算了3种跨高比简支梁受均匀分布力的动力响应，从图中可以看出随着控制体数的增加响应曲线趋近于精确解并且当跨高比为100时不存在剪切自锁现象，进而验证了有限体积法可以应用于Timoshenko梁模型的动力学分析。

3.4.2 算例2

一简支梁的截面宽度为T;所承受载荷为F1和F2，作用的位置和载荷大小如图12、13所示;材料密度为7 800kg/m3，泊松比为0.3，杨氏模量为210GPa，剪切修正系数为0.833,选取的时间步长10-6s，计算梁中点响应。

图12 载荷作用位置示意图Fig. 12 Sketch of pined-pined beam under two concentrated forces

图13 载荷-时间曲线(集中载荷)Fig. 13 Load-time curve(concentrate load)

首先分别利用有限元法和有限体积法计算了梁截面高度为0.2m、宽度为0.1m即跨高比为5, 0.01s的梁中点位移响应，结果如图14(a)所示。然后计算了梁截面高度为0.05m、宽度为0.1m即跨高比为20, 0.01s的梁中点位移响应，结果如图14(b)所示。最后计算了梁截面高度为0.01m、宽度为0.1m即跨高比为100, 0.05s的梁中点位移响应，结果如图14(c)所示。

(a) L/H=5

(b) L/H=20

(c) L/H=100图14 简支梁受集中载荷位移响应曲线Fig. 14 Displacement-time curve for simply-supported beam under concentrate load

此算例计算了3种跨高比简支梁受不同相位多激励的动力响应，通过与有限元软件计算结果比较，可以发现在相同离散单元下，有限体积法可以相对准确预测梁受不同相位多激励响应，并且同时适应于细长梁和深梁，不存在剪切自锁现象。

4 结论

通过以上4个算例可以得到如下结论:

1)有限体积法可应用于不同跨高比的梁并且不存在有限元中Timoshenko梁模型的剪切自锁现象，即可以利用有限体积法对不同跨高比的梁只用一种模型即可得到相对准确数值解。

2)验证了有限体积法可以应用Timoshenko梁模型对梁进行静力分析，特征值和动力响应分析，并且其数值结果与精确解和有限元解吻合较好。

3)利用有限体积法可以预测梁受均布载荷以及不同相位多激励的梁的响应。

[1]包刚强, WANG Erke, 郝清亮, 等. 对主流有限元软件控制剪切自锁和沙漏模式的比较和研究[C]//第八届中国CAE工程分析技术年会暨2012全国计算机辅助工程(CAE)技术与应用高级研讨会论文集. 成都, 2012: 8.

[2]MACDONALD P W. The computation of transonic flow through two-dimensional gas turbine cascades[D]. ASME, 1971: 71-89.

[3]MACCORMACK R W, PAULLAY A J. Computational efficiency achieved by time splitting of finite difference operators[D]. San Diego:AIAA, 1972: 72-154.

[4]RIZZI A W, INOUYE M. Time-split finite-volume method for three-dimensional blunt-body flow[J]. AIAA Journal, 1973, 11(11): 1478-1485.

[5]PATANKAR S V. Numerical heat transfer and fluid flow, series in computational methods in mechanics and thermal sciences[M]. Washington, DC: CRC Press, 1980: 5-20.

[6]HIRSCH C. Numerical computation of internal and external flow, Vol. I[M]. Chichester: Wiley, 1988: 17-38.

[7]WHEEL M A. A finite volume method for analysing the bending deformation of thick and thin plates[J]. Computer Methods in Applied Mechanics and Engineering, 1997, 147(1/2): 199-208.

[8]FALLAH N, HATAMI F. A displacement formulation based on finite volume method for analysis of Timoshenko beam[C]//Proceedings of the 7th International Conference on Civil Engineering. Tehran, Iran, 2006.

[9]BATHE K J. Finite element procedures[M]. New Jersey: Prentice Hall, 1996: 770-774.

[10]铁摩辛柯 S. 材料力学[M]. 北京: 科学出版社, 1978: 210-216.

[11]COWPER G R. The shear coefficient in Timoshenko’s beam theory[J]. Journal of Applied Mechanics, 1966, 33(2): 335-340.

[12]张义民. 机械振动[M]. 北京: 清华大学出版社, 2007: 187-198.

Static and dynamic analysis of Timoshenko beam model based on the finite volume method

JING Lilong, ZHANG Wenping, MING Pingjian, FU Lirong, LIU Xiaogang

(College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China)

In order to explore a numerical simulation method based on the Timoshenko beam model, a study was done on beam numerical simulation using the Timoshenko beam model, based on the finite volume method (FVM). In order to examine the beam's shear deformation, the beam model was discretized by FVM, and static and dynamic analyses were conducted. After first calculating some typical examples, the derived numerical results and the analytic solutions with FVM, a comparison was made with the solution by FVM. It is shown that FVM provides high precision analysis, with no shear-locking phenomenon for thin and long beams when discretizing Timoshenko beam based on FVM. This validates FVM for analyzing Timoshenko beam static bending, inherent characteristics, and dynamic response problems.

finite volume method; Timoshenko beam; static analysis; dynamic analysis; shear locking phenomenon; natural frequency; displacement response

2014-08-28.

时间：2015-07-15.

中央高校基本科研业务费专项资金资助项目(HEUCF130302).

井丽龙(1987-), 男, 博士研究生; 张文平(1956-)，男，教授，博士生导师； 明平剑(1980-), 男, 副教授.

明平剑, E-mail: pingjianming@hrbeu.edu.cn.

10.3969/jheu.201408044

TK124

A

1006-7043(2015)09-1217-07

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150715.1728.008.html