复合材料圆柱壳体水下非线性屈曲数值分析

潘光, 鲁江锋，沈克纯

(西北工业大学 航海学院，陕西 西安 710072)

复合材料圆柱壳体水下非线性屈曲数值分析

潘光, 鲁江锋，沈克纯

(西北工业大学 航海学院，陕西 西安 710072)

为解决水下复合材料仿真精度低的问题，采用非线性数值分析方法对复合材料圆柱壳体的水下屈曲行为进行研究。通过算例表明了非线性屈曲数值分析与试验结果的吻合性较好，验证了数学模型和计算方法的有效性。对比了铝合金、Carbon/Epoxy、Boron/Epoxy和Glass/Epoxy4种材料圆柱壳体的水下非线性屈曲行为，结果表明纤维的拉伸模量对于圆柱壳体的耐压能力有较大影响，Carbon/Epoxy是水下圆柱壳体比较理想的一种材料，最后分析了矩形、T形和L形肋骨复合材料圆柱壳体的水下非线性屈曲行为，通过分析可知，T形肋骨对于提高圆柱壳体的屈曲压力是最明显的。研究结果对于复合材料在水下的应用及研究有较大的参考价值和指导作用。

复合材料；圆柱壳体；非线性屈曲；缺陷系数；弧长法；有限元；肋骨

圆柱壳体作为基本的单元在飞行器舱段、火箭壳体、发射管、船舶桅杆、传动轴、石油管道、鱼雷壳体等领域起着很重要的作用，而且复合材料以其机械性能的可设计性、比强度高、耐高温、耐腐蚀、工艺性好、使用寿命长、维护方便[1]等性能在航天、航空和航海领域得到了广泛的应用，所以对于圆柱复合材料壳体的研究就显得意义格外重大。复合材料在航天、航空的应用比航海广泛得多，航天、航空方面圆柱壳体主要受到轴向压缩载荷，轴向压缩屈曲破坏是其主要的破坏形式[2]，所以对复合材料圆柱壳体的研究较多的是集中在轴向压缩的屈曲破坏，而对于复合材料圆柱壳体水下屈曲破坏研究较少。Chihdar Yang等[3]应用一级剪切变形理论研究了长径比较大圆柱壳体承受水下均布压力时的线性屈曲，结果与试验数据比较一致，误差在20%左右。Seong-Hwa Hur等[4]应用ACOSwin有限元软件进行了复合材料圆柱壳体水下非线性屈曲分析，屈曲模态形状与试验结果基本相同，计算结果与试验有15.5%的误差。Chul-Jin Moon等[5]同样应用ACOSwin有限元软件对纤维缠绕复合材料圆柱壳体进行了数值仿真和实验对比，发现屈曲压力是壳体的最大承受压力，壳体屈曲之后直接导致破坏。Tanguy Messager等[6]应用第三剪切变形理论研究了薄壁圆柱壳体的线性屈曲，并通过遗传算法优化最佳铺层顺序，高继和[7]则重点论述水下航行体用复合材料的发展。本文针对一定厚度的复合材料圆柱壳体，承受水下均布压力和轴向载荷时，考虑到试样的初始几何缺陷，引入了缺陷系数的概念，进行了非线性屈曲数值分析。

1 非线性屈曲

1.1 非线性屈曲分析介绍

屈曲分析用来求解壳体失稳时的临界压力和屈曲模态形状，包括线性特征值屈曲和非线性屈曲两大类。图1是非线性屈曲分析曲线图，点画线曲线交叉点处的临界压力值是特征值屈曲的计算结果，实线曲线的首个峰值是非线性屈曲的计算结果，可以看出非线性屈曲分析比线性屈曲分析值偏低，虚线曲线是实际的动态响应，非线性屈曲更加符合实际情况，比线性屈曲分析更加准确[8]。屈曲以屈曲载荷为分水岭分为前屈曲和后屈曲，本文只研究前屈曲。

图1 非线性屈曲变形曲线Fig. 1 Nonlinear buckling curve

线性特征值屈曲作为屈曲分析的不保守解，可以为非线性屈曲提供参考，当初始缺陷无法可靠估计时，线性屈曲模态形状可以作为几何缺陷，通常提取一阶模态乘以一个缺陷系数(DF)，线性屈曲压力还可以作为非线性分析的施加载荷，通过观察线性屈曲特征值的分布，判断壳体对几何缺陷的敏感性[9]。

1.2 一级剪切变性理论

本文基于Reisnner-Mindin[10-12]一级剪切变性理论进行数值分析，描述了圆柱壳体承受水压时的动力学方程、能量方程和边界条件，屈曲问题最终应用Ritz[13]方法转化成求解矩阵特征值的问题。

1.2.1 动力学方程

坐标系的定义如图2所示，包括x,s,z3个分量，方向分别是圆柱的轴向、切向和径向，坐标原点位于柱体左端的中径，3个方向的位移分量分别是u、v、w，可表示为

(1)

式中：u0、v0代表柱体中面的位移;F1、F2是相应的弯曲斜度，根据柱体的几何尺寸，应变分量可由u0、v0、F1,F2,w表示如下：

(2)

式中：R是柱体的中面半径，将式(1)代入式(2)可以得到由中面位移和弯曲斜度表示的应变场。

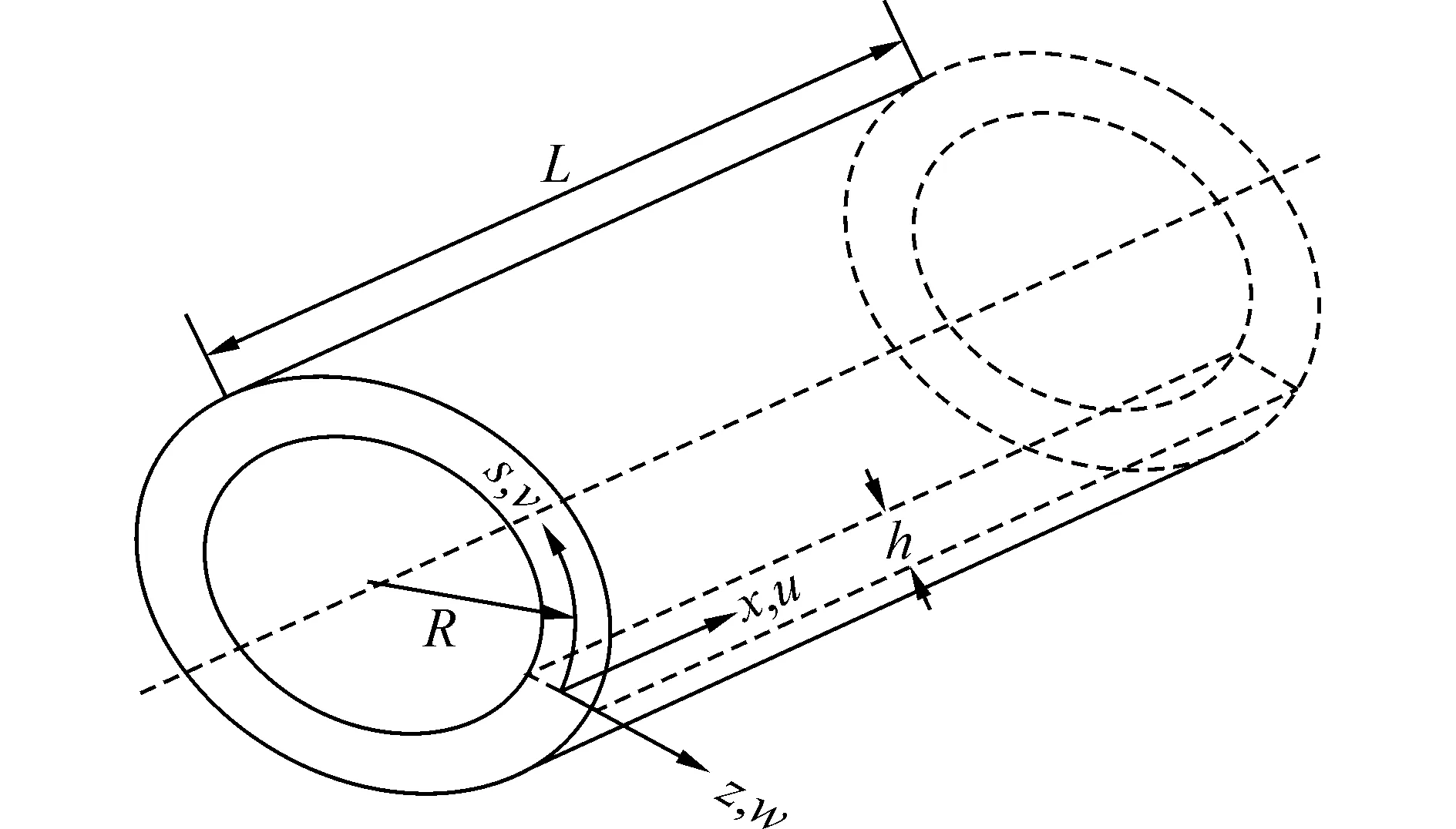
图2 坐标系及模型尺寸Fig. 2 Coordinates and model dimensions

1.2.2 能量方程

圆柱体置于水下压力场时，涉及到的能量有总应变能U、水压所做的功W、由于水压和中面延伸引起的潜在能量V:

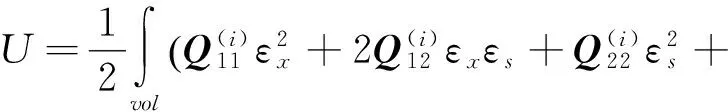
(3)

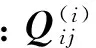
W=-∬pwdxds

(4)

式中：p是承受的水下均布压力。

(5)

1.2.3Ritz方法

根据Ritz方法，屈曲压力可以通过总能量的变化为零来得到，即满足下式：

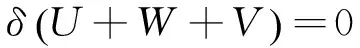
(6)

模型一端固定，一端允许轴向位移，因此边界条件如下：x=0处，

u=0,v0=0,w=0,F2=0

(7)

x=L处，

v0=0,w=0,F2=0

(8)

式(3)～(6)构成了屈曲方程，将式(7)、(8)代入屈曲方程求解就可以得到屈曲压力，以矩阵的形式表达如下：

(Kf-pKg)x=0

(9)

式中：Kf是刚度矩阵，Kg是应力刚度矩阵，x是特征向量。

2 算例验证

针对文献 [4]中的有限元模型，本文利用大型通用有限元软件ANSYS中的弧长法进行非线性屈曲计算，通过多次计算，设置了合适的网格尺寸，大大提高了精度。

为了施加恰当的几何缺陷，需要对缺陷系数(DF)进行可靠的估计,缺陷系数等于制造误差(MT)与一阶线性特征值屈曲最大节点位移(MD)的比值，文献[4]中制造误差是0.17 mm，最大节点位移是1.035 mm。

(10)

表1是网格的相关性验证，可以看出网格尺寸对于计算结果有较大的影响，当网格尺寸过大时，计算精度会降低，达不到分析的目的，当网格尺寸过小时，对计算机的要求特别高，而且计算时间会很长。当网格尺寸在逐渐减小时，相对误差变化平缓，计算结果趋于一个稳定值0.57 MPa，考虑到计算时间，本文中选择15 mm作为计算的网格尺寸。

表1 网格相关性验证

图3是建立的有限元模型及边界条件，坐标系位于模型的A端，X轴与模型旋转轴重合，模型沿着圆柱周向是2.52 mm厚的复合材料，复合材料选用Carbon/Epoxy，铺层顺序是[0/90]12T，左端A敞开，右端B是13 mm后的碳钢端盖，A端沿着圆柱外径施加固定约束，B端沿着圆柱外径只允许轴向位移，周向和右端施加均布压力载荷来模拟水下压力场。

图4是有限元模型位移最大节点(节点号1078)的压力-位移变化曲线，包括X方向位移(UX)、Y方向位移(UY)和总位移(SUM)跟随压力的变化曲线。从图中可以看出，X方向位移随压力的变化程度要大于Y方向的，但3条曲线的变化趋势基本相同，在0.57MPa曲线达到峰值，随后压力的变化带来位移的急剧改变，表明圆柱壳体已经发生屈曲现象。文献 [4]中CTM1试样的试验壳体屈曲压力是0.55MPa，本文中ANSYS计算的屈曲压力是0.577MPa，相对误差是5%，远远小于文献[4]中利用ACOSwin计算的误差值(15.5%)，与试验结果十分吻合。

图3 有限元模型及边界条件Fig. 3 Finite element model and boundary conditions

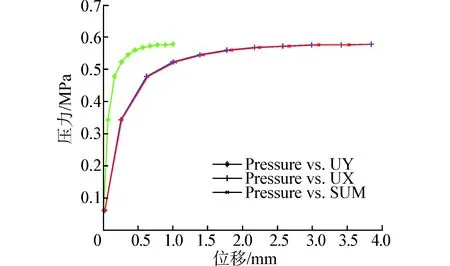
图4 节点1078压力-位移曲线Fig. 4 Pressure vs. displacement curve of node 1078

图5 屈曲模态形状Fig. 5 Buckling mode shape

屈曲模态形状是验证计算是否正确的很重要的一个指标，只有屈曲波形较好地与试验屈曲波形重合才能证明计算的正确[5]。图5是屈曲分析的屈曲模态形状，其中，周向有4个波，轴向有一个长波，与文献 [4]中Marc非线性分析的波形十分相似，尽管波形的曲率与长度与试验略有差异，但是波形基本相同，较好地预测了圆柱壳体屈曲模态形状。复合材料的抗拉能力远远大于其抗压能力，图5中模型中部凹陷部分纤维承受的是压应力，其应力和应变也是最大的，1078号节点就位于这个位置。

3 材料对壳体屈曲的影响

为了显示复合材料壳体相对于传统壳体的优越性和选择一个更适合于水下的复合材料，对比了不同材料壳体屈曲行为。严酷的水下环境要求壳体材料能够以承受高的外部压力、具有良好的耐腐蚀性、高的比强度、良好的吸声性能、良好的制造性能、较长的使用寿命、合理的材料费用，如果有防火要求，还得考虑材料对于温度的敏感性[14]。因此，本文选择了满足以上条件的传统材料铝合金和3种复合材料Carbon/Epoxy[4]、Boron/Epoxy[15]、Glass/Epoxy[6]，材料的机械性能如表2所示。

表2 材料弹性性能

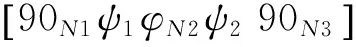
薄壁壳体的失效主要是两方面，一个是壳体的屈曲，另一个是材料的破坏[16-17]，大量研究表明屈曲破坏是复合材料圆柱壳体的主要破坏形式[18]，所以本文只研究圆柱壳体的屈曲行为。

圆柱壳体的几何尺寸L(长度)×d(中径)=600mm×300mm。图6是不同材料圆柱壳体屈曲压力-铺层厚度的变化曲线，从图中可以看出随着铺层厚度的增加屈曲压力显著增大，Boron/Epoxy圆柱壳体的屈曲压力最大，Glass/Epoxy圆柱壳体的屈曲压力最小，铝合金与Carbon/Epoxy圆柱壳体屈曲压力居中且相近，在厚度是0.19mm之前Carbon/Epoxy圆柱壳体屈曲压力大于铝合金圆柱壳体屈曲压力，在0.19mm之后Carbon/Epoxy圆柱壳体屈曲压力小于铝合金圆柱壳体屈曲压力。然而铝合金圆柱壳体在屈曲之前就发生了材料的失效,所以其实际屈曲压力是低于计算结果的。Glass/Epoxy圆柱壳体的屈曲压力-铺层厚度曲线近似为线性变化，其他3条曲线近似为指数变化。

图6 不同材料壳体屈曲压力-铺层厚度曲线Fig. 6 Buckling pressure vs. ply thickness curves of different materials shells

3种复合材料的基体都是Epoxy，不同的是纤维的材料，为了便于分析列出3种纤维性能[19]对比，如表3所示。

表3 纤维性能对比

从4种材料的屈曲曲线可以看出，Boron/Epoxy屈曲压力最大，是最适宜的水下耐压壳体材料，然而Boron/Epoxy价格很高，而且密度(2.11 g/cm3)较大，对于只要求提高屈曲压力的情况下适用；Glass/Epoxy屈曲压力最小，价格较低，密度(1.85 g/cm3)比Boron/Epoxy小，对于屈曲压力要求不高追求性价比的情况下适用；铝合金屈曲压力介于Carbon/Epoxy与Glass/Epoxy之间，但密度(2.77 g/cm3)很大，复杂壳体的加工工艺复杂，对于减重要求不高结构不复杂的情况下适用；Carbon/Epoxy屈曲压力较大，密度(1.32 g/cm3)最小，比强度高，价格适中，对于减重要求高追求综合性能的情况下适用。

图7是铺层厚度是0.105 mm时4种材料的屈曲模态形状对比图，波形各不相同，铝合金壳体周向有5个波，其他3种复合材料壳体周向有4个波，但波形的分布位置和大小各不相同。

复合材料圆柱壳体承受水压时，根据能量法计算其压缩强度如式(11)所示[20]，主要受到基体的剪切模量和纤维体积分数的影响，当压力达到一定值时就会引起纤维的微观屈曲使基体产生剪切变形，然后发生壳体整体发生变形，此时纤维主要受到拉伸作用，Boron纤维的拉伸模量最大，所以其抵抗变形能力就越强，Boron/Epoxy圆柱壳体的耐压能力就越好。

(11)

式中：Gm是基体的剪切模量，Vf是纤维的体积分数，β是修正系数。

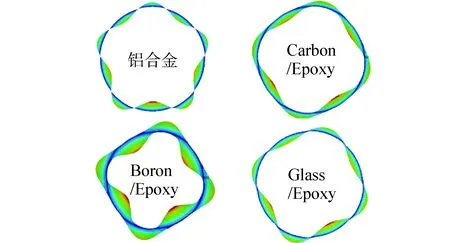
图7 不同材料壳体屈曲模态形状Fig. 7 Buckling mode shapes of different materials' shells

4 结构对壳体屈曲的影响

带肋骨各向同性材料圆柱壳体的屈曲研究已经很成熟，而带肋骨复合材料圆柱壳体的屈曲研究较少，因此，本文中研究了不同的结构包括无肋骨、矩形肋骨、T形肋骨、L形肋骨等壳体屈曲的影响，材料统一选择Carbon/Epoxy。

TanguyMessager[21]指出圆柱壳体肋骨的周向加强对于提高其承受水压的能力起主要作用，轴向的加强基本不起作用，所以本文中研究的肋骨都是周向肋骨。

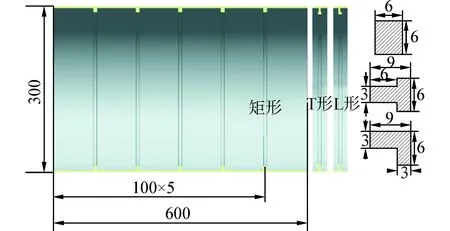
图8 壳体截面图及肋骨尺寸Fig. 8 Cross-sectional view of shell & ribs dimensions

图8是圆柱壳体截面图及肋骨尺寸，矩形、T形和L形3种肋骨的截面积都是36mm2，分布位置相同，沿着轴向等间距分布，肋骨分布间距是100mm，共有五根肋骨，圆柱壳体的几何尺寸L×d=600mm×300mm，圆柱壳体铺层厚度是0.15mm，铺层顺序是[0/90]10T，壳厚3mm。

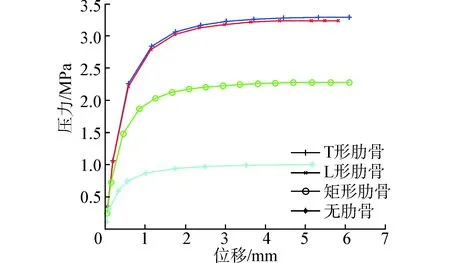
图9 不同肋骨壳体压力-位移曲线Fig. 9 Buckling pressure vs. displacement curves of shells with different ribs

图10 不同肋骨壳体屈曲模态形状Fig. 10 Buckling mode shapes of shells with different ribs

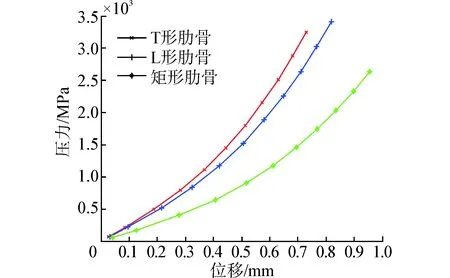
图11 不同肋骨壳体压力-位移曲线Fig. 11 Pressure vs. displacement curves of shells with different ribs

图9是3种肋骨圆柱壳体的压力-位移曲线，观察4条曲线峰值点对应的Y坐标值，可以得到T形、L形、矩形和无肋骨壳体的屈曲压力分别是3.28、3.24、2.28和0.99MPa，可见肋骨大大增强了壳体的耐压能力，且不同形式的肋骨对壳体的增强能力是不同的。图10是不同肋骨壳体屈曲模态波形图，其中无肋骨壳体有4个周向波，带肋骨壳体有3个周向波，T形和L形肋骨壳体屈曲模态波形是相同的，但它们与矩形肋骨壳体的波形分布不同。

由于3种肋骨的截面积相同，分布位置也相同，而3种肋骨壳体的屈曲压力却不同，本文得出以下结论：T形肋骨的刚度>L形肋骨的刚度>矩形肋骨的刚度。为了验证以上的结论，本文对比了3种肋骨在水下的压力-位移曲线图，如图11所示，可以看出，T形肋骨屈曲压力>L形肋骨屈曲压力>矩形肋骨屈曲压力，与结论相符。

5 结论

本文对圆柱复合材料壳体进行了非线性屈曲分析，对比了不同材料壳体之间、不同结构壳体之间的屈曲行为，得出以下结论：

1)引入恰当的初始几何缺陷，对复合材料壳体进行非线性屈曲数值分析，其结果与实验数据具有较好的一致性。

2)水下复合材料壳体耐压时，首先引起纤维的微观屈曲使基体产生剪切变形，然后发生壳体整体发生变形，纤维受到拉伸，其拉伸模量对壳体屈曲压力的影响较大，意味着水下复合材料应该选择拉伸模量较高的纤维。

3)相对于其他形式的肋骨，T形肋骨的耐压能力更好，其对复合材料壳体的整体刚度有较大增强，提高了壳体的屈曲压力，说明肋骨的形状对于壳体整体的刚度有较大影响，有必要对肋骨形状和尺寸进行优化设计以提高壳体的刚度。

[1]SEN R, MULLINS G. Application of FRP composites for underwater piles repair[J]. Composites Part B: Engineering, 2007, 38(5): 751-758.

[2]OHGA M, WIJENAYAYA A S, CROLL J G A. Buckling of sandwich cylindrical shells under axial loading[J]. Steel & Composite Structures, 2005, 5(1): 1-15.

[3]YANG C, PANG S S, ZHAO Y. Buckling analysis of thick-walled composite pipe under external pressure[J]. Journal of Composite Materials, 1997, 31(4): 409-426.

[4]HUR S H, SON H J, KWEON J H, et al. Postbuckling of composite cylinders under external hydrostatic pressure[J]. Composite Structures, 2008, 86(1): 114-124.

[5]MOON C J, KIM I H, CHOI B H, et al. Buckling of filament-wound composite cylinders subjected to hydrostatic pressure for underwater vehicle applications[J]. Composite Structures, 2010, 92(9): 2241-2251.

[6]MESSAGER T, PYRZ M, GINESTE B, et al. Optimal laminations of thin underwater composite cylindrical vessels[J]. Composite Structures, 2002, 58(4): 529-537.

[7]高继和. 水下航行体用复合材料的发展[J]. 玻璃钢/复合材料, 2003 (5): 42-45. GAO Jihe. Composite development in underwater vehicles[J]. Fiber Reinforced Plastics/Composite, 2003(5): 42-45.

[8]SUBRAMANI T, SUGATHAN A. Finite element analysis of thin walled-shell structures by ANSYS and LS-DYNA[J]. IInternational Journal of Modern Engineering Research, 2012, 2: 1576-1587.

[9]CHEN T. On introducing imperfection in the non-linear analysis of buckling of thin shell structures[D]. Delft: Delft University of Technology, 2014:65-73.

[10]REISSNER E. The effect of transverse shear deformation on the bending of elastic plates[J]. Journal of Applied Mechanics, 1945, 12: 69-77.

[11]MINDLIN R D. Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates[J]. Journal of Applied Mechanics, 1951, 18(1): 31-38.

[12]REISSNER E. On the theory of bending of elastic plates[J]. Journal of Mathematical Physics, 1944, 23: 184-191.

[13]GAVALAS G R, EL-RAHEB M. Extension of Rayleigh-Ritz method for eigenvalue problems with discontinuous boundary conditions applied to vibration of rectangular plates[J]. Journal of Sound and Vibration, 2014, 333(17): 4007-4016.

[14]ROSS C T F. A conceptual design of an underwater vehicle[J]. Ocean Engineering, 2006, 33(16): 2087-2104.

[15]TANOV R, TABIEI A. A simple correction to the first-order shear deformation shell finite element formulations[J]. Finite Elements in Analysis and Design, 2000, 35(2): 189-197.

[16]苟文选. 材料力学[M]. 2版. 北京: 科学出版社, 2010: 240-242. GOU Wenxuan. Material mechanics[M]. Beijing: Science Press, 2010: 240-242.

[17]GROENWOLD A A, HAFTKA R T. Optimization with non-homogeneous failure criteria like Tsai-Wu for composite laminates[J]. Structural and Multidisciplinary Optimization, 2006, 32(3): 183-190.

[18]闫光. 轴压载荷下复合材料层合圆柱壳的设计与试验研究[D]. 长春：吉林大学, 2013:128-129. YAN Guang. The design and experimental study of composite cylindrical shell under axial compressive load[D]. Changchun: Jilin University, 2013:128-129.

[19]SHACKELFORD J F. The CRC materials science and engineering handbook[M]. Boca Raton,FL: CRC Press, 2010: 30-32.

[20]乔生儒. 复合材料细观力学性能[M]. 西安: 西北工业大学出版社, 1997: 28-30. QIAO Shengru. Micro mechanical properties of composites[M]. Xi'an: Northwestern Polytechnical University Press, 1997: 28-30.

[21]MESSAGER T, CHAUCHOT P, BIGOURDAN B. Optimal design of stiffened composite underwater hulls[C]//III European Conference on Computational Mechanics:Solids, Structures and Coupled Problems in Engineering. Lisbon,Portugal, 2006:239-248.

Nonlinear numerical buckling analysis of composite underwater cylindrical shell

PAN Guang, LU Jiangfeng, SHEN Kechun

(College of Marine Engineering, Northwestern Polytechnical University, Xi’an 710072, China)

In order to solve low accuracy in underwater composite simulation, the nonlinear numerical analysis method was used to study underwater buckling behaviors of a composite cylindrical shell. The results show that the simulation and an experiment are consistent with each other, which validates the effectiveness of the model and the method. The underwater nonlinear buckling behaviors of an underwater shell made of four kinds of materials , including aluminum, carbon/epoxy, boron/epoxy and glass/epoxy, were contrasted. The results show that the tensile modulus of fibers have great impact on the pressure capacity of the cylindrical shell. Carbon/epoxy is an ideal material for cylindrical shells subjected to hydrostatic pressure.Finally, the underwater nonlinear buckling behaviors of stiffened composite cylindrical underwater shells with different shaped ribs, such as rectanglar, T-shaped, and L-shaped ribs, were studied. The results show that the T-shaped ribs are best for improving the buckling pressure of cylindrical shells. The results of this paper have an important reference value and guidance function for underwater application and study of composite materials.

composites; cylindrical shell; nonlinear buckling analysis; defect factor; arc-length method; finite element analysis; rib

2014-12-18.

时间：2015-07-28.

国家自然科学基金资助项目(51279165,51479170).

潘光(1969-), 男,教授,博士； 鲁江锋(1984-), 男,硕士研究生.

鲁江锋, E-mail：windf.23@gmail.com.

10.3969/jheu.201412056

TB332

A

1006-7043(2015)09-1159-06

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150728.1414.005.html