相交轴螺旋非圆齿轮啮合传动研究

宋洪舟,魏世民,廖启征,郭磊

(北京邮电大学 自动化学院，北京 100876)

相交轴螺旋非圆齿轮啮合传动研究

宋洪舟,魏世民,廖启征,郭磊

(北京邮电大学 自动化学院，北京 100876)

为了将非圆齿轮应用到变速器中，提出一种实现相交轴变传动比运动的螺旋非圆齿轮副，并对其啮合原理进行研究。定义了该非圆齿轮的螺旋节曲线，给出传动比公式及齿轮副周向纯滚动条件，建立了基于包络法加工非圆齿廓数学模型；通过描述圆柱齿轮的各段齿面方程，结合共轭齿廓啮合基本定理，推导出了螺旋非圆齿轮的齿面方程，并验证两者瞬时啮合状态为线接触；利用数值计算软件，生成了精确的非圆齿面，分析了左右非圆齿廓外观特征，为进一步研究和应用提供了理论基础。

齿轮；螺旋非圆齿轮；相交轴； 啮合原理；齿廓；线接触

非圆齿轮的最大特点是能够传递两轴之间非匀速运动，它综合了齿轮与凸轮机构优点，既能实现准确运动规律，又能传递较大的动力[1]。目前，非圆齿轮传动在许多场合均有应用，例如卵形流量计、非圆行星液压马达[2]、新型摆线减速器[3]、汽车差速器[4-5]、农业机械[6]等设备中。

近年来，国内外学者对非圆齿轮相关研究取得多方面进展，谭伟明、吴序堂等人建立了非圆齿轮加工简化模型[7-10]，其齿廓可由齿条对非圆齿轮展开包络；夏继强提出非圆锥齿轮几何设计方法[11]；林超等讨论了不同球面节曲线下的传动特性，并对非圆锥齿轮球面渐开线插齿方法进行了分析[12-13]。

多圈非圆齿轮是一种特殊类型的非圆齿轮[14]，它能使传动比函数的再现角度区间大于360°，但齿轮在转动过程中，必须有微小的轴向移动才能正确啮合，属于空间啮合范畴，因此齿形较为复杂。

本文以多圈非圆齿轮外观为研究对象，尝试将此特点应用于锥形齿轮组变速装置中，提出螺旋非圆齿轮传动，并研究齿轮副啮合原理，建立齿廓形成数学模型，分析齿面几何特征。

1 螺旋非圆齿轮应用构思

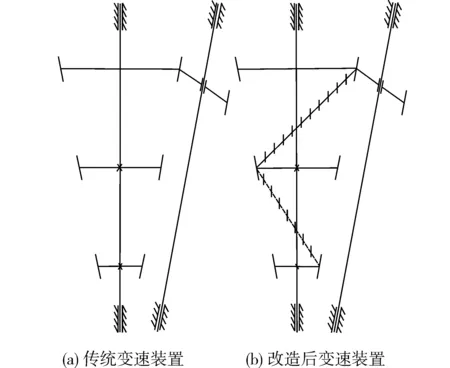
图1 锥形齿轮组变速传动装置简图Fig. 1 Sketch of conical gear transmission set

沈谦等曾设计出锥形齿轮组变速装置[15-16]，该装置采用相交轴传动，主动轮是渐开线圆柱齿轮，从动轮由一系列变厚齿轮组成，如图1(a)，这种变速装置体积小，容易达到多档位变化，但当改变档位时，必须切断动力，手动选择传动级，导致动力传递不连续。为实现自动变速功能，参照多圈非圆齿轮螺旋外观，在两级变厚齿轮之间设置螺旋非圆齿，如图1(b)，利用非圆齿轮的特殊形状和运动规律逐渐改变传动比。所有非圆齿必须连同各级变厚齿轮处在同一锥面上，主动圆柱齿轮在转动过程中，同时沿轴向滑移，便能与锥面上的非圆齿啮合传动，因此有必要进一步探讨两者之间正确啮合条件，以及非圆齿廓形状，从而验证这种传动类型的可行性。

2 螺旋节曲线

一对齿轮相对运动速度为零的点，在各自回转坐标系中的轨迹构成瞬心线，即节曲线。从图1(b)中可以看到，主动圆柱齿轮轴向移动，致使齿轮副的中心距和传动比改变，从而体现出非匀速特性，为了分析这种变化，可将瞬时啮合状态假想为圆柱齿轮与一定当量齿数的变厚齿轮传动。

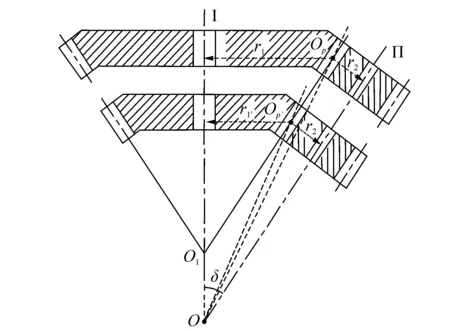
图2 圆柱齿轮与各级变厚齿轮传动Fig. 2 Transmission for cylindrical gear and each beveloid gear

图2中，圆柱齿轮与模数相同、齿数不同的两对等齿高锥齿轮传动(即为变厚齿轮)，瞬时回转轴OI是齿轮Ⅱ对齿轮Ⅰ相对运动角速度作用线，该线与回转轴线相交于同一点O，并将轴交角δ分为δ1、δ2(图中未标出)，瞬时回转轴在各自回转坐标系中构成瞬轴面。根据角速度矢量合成几何关系，得到传动比表达式:

(1)

进一步推导,得

(2)

为确定变厚齿轮的齿顶、齿根等参数，假想变厚齿轮的一个圆锥面与圆柱齿轮分度圆柱面相切于一条直线O1OP，并与瞬时回转轴交于节点OP，节点至两齿轮轴线的距离r1称为节径，传动比又可用节径之间的比值来确定：

(3)

由于变厚齿轮齿数不同，圆柱齿轮分别与之啮合时，可得到不同传动比，而节点从OP变动到OP′，锥齿轮节径由r1变为r1′，因此每对齿轮具有不同的瞬轴面，但节点OP、OP′始终处在同一圆锥面上。

为描述圆柱齿轮与螺旋非圆齿轮每一位置传动比连续改变的运动特性，节点在圆锥面上的螺旋运动用曲线表示，该曲线定义为螺旋节曲线，见图3。

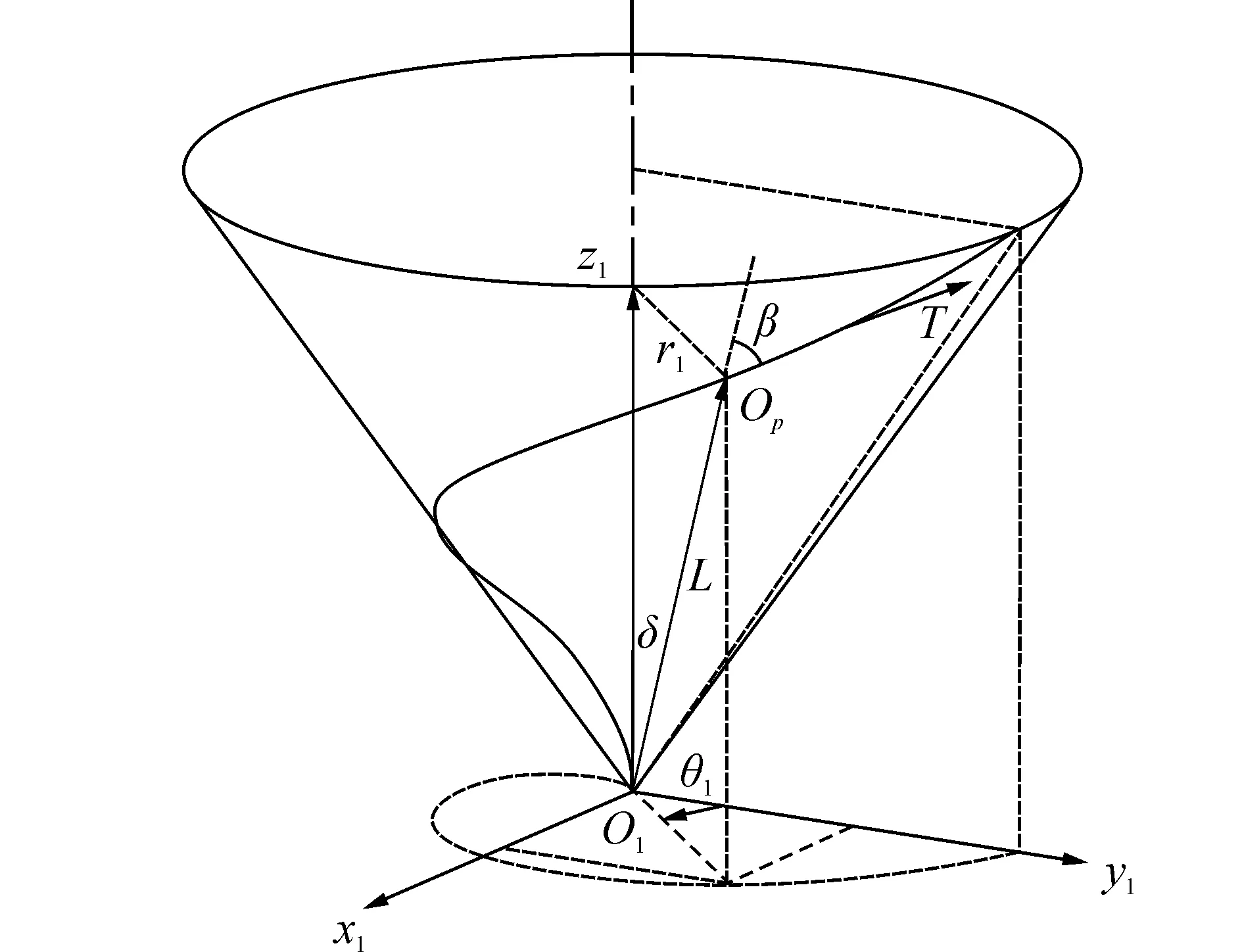
图3 螺旋节曲线Fig. 3 Spiral pitch curve of non-circular gear

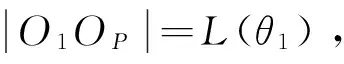
O1OP=L(θ1)sinδsin(θ1i1)+

sinδcos(θ1j1)+cos(δk1)

(4)

式中：θ1是失径极角，以y1轴为基准顺时针计量：依据前面分析，螺旋节曲线与圆柱齿轮节圆的切点OP，在圆周方向速度保持相等的关系：

VT=ω1r1=ω2r2

(5)

齿轮副传动比函数i12表示为

(6)

螺旋曲线在坐标平面x1O1y1上的投影曲线弧长应与圆柱齿轮节圆弧长相等，即

(7)

式中：θ1、θ1′、θ2、θ2′为各齿轮转动前后的极角。

3 螺旋非圆齿轮包络数学模型

3.1 空间啮合坐标系建立

分别用代号Ⅰ、Ⅱ表示螺旋非圆齿轮与圆柱齿轮(见图4)，全局固定坐标系S0(O0-x0y0z0)及非圆齿轮固联坐标系S1(O1-x1y1z1)的原点均在圆锥顶点处，坐标轴z1即是齿轮Ⅰ回转轴线。为简化坐标系，将坐标平面x0O0z0与两齿轮回转轴线所确定的平面重合，初始位置时，坐标系S0S1重合。

圆柱齿轮必须作复合运动才能同螺旋非圆齿轮正确啮合，分别用浮动坐标系S2′(O2′-x2′y2′z2′)和固联坐标系S2(O2-x2y2z2)来描述齿轮Ⅱ的轴向移动运动与圆周转动；坐标原点O2,O2′在圆柱齿轮的节圆平面上，y2′轴方向用右手螺旋定则确定，初始位置时，各坐标轴和原点均是重合的。

图4 螺旋非圆齿轮包络数学模型Fig. 4 Mathematical model for spiral non-circular gear

根据第2节中节曲线简化原理，节圆与锥面螺旋节曲线的切点记为OP，为表示该点在锥面上运动情况，建立两齿轮中间关联浮动坐标系SP(OP-xPyPzP)，令坐标分量xP、yP、zP与x0、y0、z0对应保持平行。

图4中，r2为圆柱齿轮节径，非圆齿轮节径r1为节点至非圆齿轮回转轴线的距离，节点在圆锥母线上的长度用L表示，两者几何关系为：r1=Lsinδ。当齿轮副转动到任意位置时，坐标轴x0与x1按逆时针转动方向计量的角度用φ1表示，图4右侧俯视图中可以看到，锥面螺旋节曲线极角θ1与之计量方向相反，故φ1=-θ1；对于圆柱齿轮，同样存在角度φ2=-θ2。

至此，容易找到从坐标系S1到坐标系S的变换关系和变换矩阵：R1=Ms1s0R0

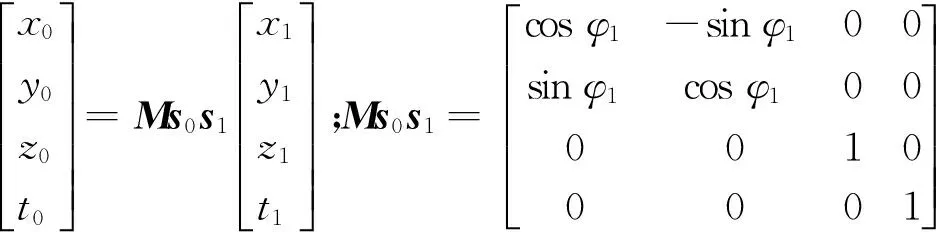
(8)

同理，其他坐标系之间的变换矩阵：

Ms0sP,Ms2′s2,MsPs2′,Ms2′s2,Ms1s2

(9)

3.2 相对运动速度表示

从全局固定坐标系S0观察，螺旋非圆齿轮做定轴转动，角速度矢量记为ω1；与之共轭的圆柱齿轮做复合运动，其运动状态分解为：坐标系S2相对坐标系S2′作定轴转动，角速度矢量记为ω2；原点O2相对固定坐标系S0沿圆锥母线方向牵连移动速度VL。设M是两齿轮齿面上瞬时接触点，该点在非圆齿轮与圆柱齿轮的速度矢量为

V1=ω1×O1M；V2=ω2×O2M+VL

(10)

圆柱齿轮齿廓曲面是已知的，M点位置矢量可表示在坐标系S2中

(11)

进一步得出两个刚体在公共切点处的相对运动速度

V12=V1-V2=

[ω1(-sinδsinφ2L-r2cosδsinφ2+

(12)

3.3 圆柱齿轮齿面参数方程

圆柱齿轮既是啮合对象，又是非圆齿廓成型刀具，轴截面内具有相同齿形，使坐标轴x2与齿槽中线重合，则左右齿廓均关于此轴对称的。圆柱齿轮参与包络的齿廓由：齿顶ab段、齿顶圆角bc段、齿侧cd段组成，对于渐开线弧段方程，采用以下方法获得。

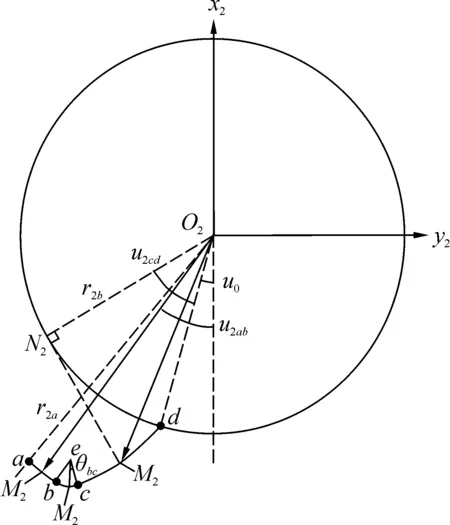
图5 圆柱齿轮截面齿廓组成Fig. 5 Tooth profile of cylindrical gear in section

设渐开线齿廓上任一流动点M2，在坐标系S2中的位置矢量表示为

(13)

利用渐开线性质得

(14)

则cd段失径方程

(15)

式中：r2b为圆柱齿轮基圆半径；u2cd为渐开线滚动角变量；lz2是齿廓齿宽方向变量；u0为渐开线起始向径到齿槽中线x2轴的夹角；符号“±,∓”上面代表齿轮右侧齿廓，下面代表左侧齿廓，i代表各轮齿位置。

i=0,1,2,3…

(16)

利用以下方程，求得cd段法线矢量:

(17)

其余ab、bc两段失径、法线矢量均类似求得

(18)

综上所述，各段齿面方程与法线矢量统一写成：

(19)

(20)

其中，以上两式的变量可以用u2表示：

u2={u2ab,θ2bc,u2cd}

(21)

3.4 啮合方程与非圆齿面方程

在图4中，点M是两齿轮齿廓的瞬时接触点，根据包络曲面非奇异条件[17]得知，两齿廓曲面在该点处必须保持相切触，并存在共同公切面和公法线，共轭齿廓啮合基本定理中规定，若使两齿廓连续相切传动，既不产生干涉，又不相互脱开，他们在切点的相对运动速度一定沿公切线方向，用矢量公式表示为

f12=n2·V12

(22)

以齿侧cd段为例，得到含参变量u2cd、lz2、φ1、φ2的啮合方程式f12cd：

f12cd=±sin(u0+u2cd)[ω1(-sinδsinφ2L-

cos(u0+u2cd)[(-sinδcosφ2L-r2cosδcosφ2-

(23)

其余各段啮合方程式：

f12(θ1,u2,lz2)={f12ab,f12bc,f12cd}

(24)

将圆柱齿轮齿面方程变换到非圆齿轮固联坐标系S1中，便能得到由包络产生的曲面族，再结合啮合方程式，消掉其中一个变量，导出非圆齿轮齿廓方程式

(25)

(26)

4 瞬时接触线

(27)

其中

u2cd∓φ2)+r2cotδ+L

(28)

圆柱齿轮齿面上瞬时接触线位置取决于参数φ2，当给定某一角度时，利用式(5)～(7)求得非圆齿轮角速度ω1、转角φ1，而锥顶角δ、基圆半径r2b、节径r2等均为常值，瞬时接触线的参数方程(27)中只含变量u2cd，显然代表一条曲线，其他两段曲面类似验证。

5 非圆齿面计算方法与验证

5.1 齿面生成流程

前面分析到，非圆齿在锥面上的布置与齿廓形状依赖于锥面螺旋节曲线，一旦确定向径L的变化规律，便能得出齿轮传动比变化曲线，也决定了圆柱齿轮发生耦合运动的轴向移动速度VL。根据以上相关公式，利用Mathematica数学软件编程，计算符合啮合方程的坐标点集，从而绘制出精确齿面，图6为螺旋非圆齿面生成流程。

图6 非圆齿面计算流程图Fig. 6 Calculation flow chart for non-circular gear

5.2 数值计算实例

表1中给出了圆柱齿轮的基本参数，并设定了锥面螺旋节曲线方程，按照上述流程编程，得到某一位置处的螺旋非圆齿廓曲面。

表1 圆柱齿轮基本参数

图7为仿真加工出的螺旋非圆齿轮齿面。下侧较窄部分为非圆齿轮齿根过渡曲面，由圆柱齿轮的齿顶圆角包络出来；上侧较宽部分为非圆齿轮齿侧曲面，由圆柱齿轮的渐开线齿面包络成型。从(a)可以看到，由于存在锥顶角，上端齿形大、齿顶较尖，下端齿形较小、齿顶较宽，呈现锥形，符合锥齿轮的外观特征。非圆齿轮的左侧齿形相比右侧齿形，在Z坐标方向错开一定的距离；(b)中，两齿廓不再关于齿厚中部对称，齿形整体向另一侧偏斜，这种变化特点正是因为圆柱齿轮转动过程中，沿轴向移动造成的，移动速度越大，齿廓相错性与不对称性越明显。

非圆轮齿两侧曲线，为圆柱齿轮包络螺旋非圆齿轮的瞬时接触线，从而验证了瞬时啮合状态仍为线接触。以摆线方程作为节曲线失径L随自身转角θ1的变化规律，在一周范围内设置两段对称的曲线，圆柱齿轮做升程与回程运动。用三维造型工具设计出了改造后的螺旋非圆齿轮变速装置虚拟模型，并通过3D打印技术加工出了实体，进一步说明了这种传动类型的可行性。

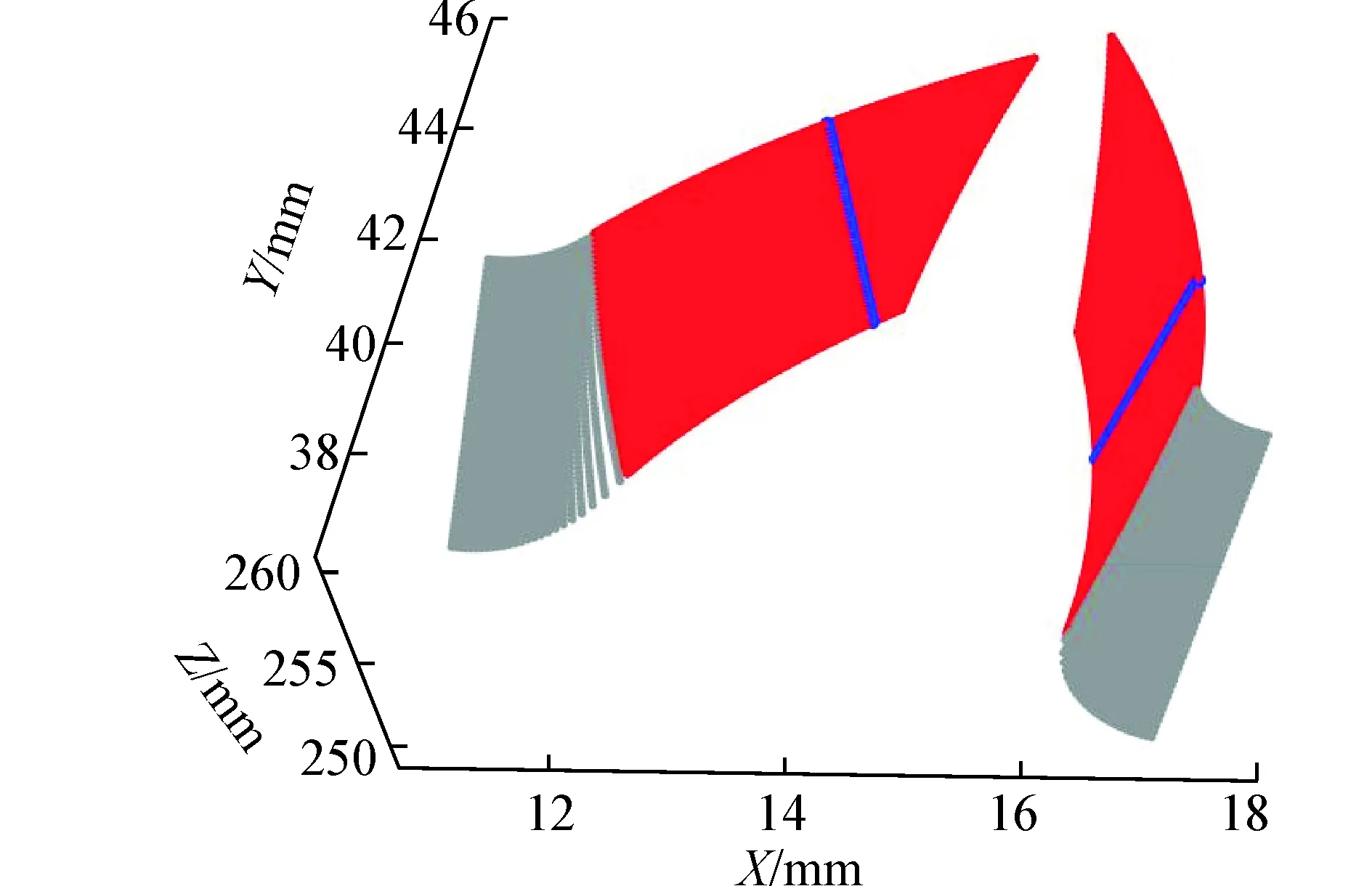
图7 螺旋非圆齿轮齿面Fig. 7 Tooth profile of spiral non-circular gear

图8 螺旋非圆齿轮三维模型Fig. 8 Three-dimensional model of spiral non-circular gear

6 结论

1) 依据多圈非圆齿轮的外观特征，提出一种实现相交轴变传动比运动的螺旋非圆齿轮，与之啮合的齿轮副被限定为圆柱齿轮，各非圆齿均布置在锥顶角为轴交角的圆锥面上，圆柱齿轮做耦合运动，才能与螺旋非圆齿轮正确啮合。

2) 以圆柱齿轮与变厚齿轮啮合传动为基础，研究相同锥顶角、模数、不同配对齿数情况下齿轮副传动比、瞬轴面变动规律，用螺旋节曲线来描述节点在非圆齿轮在固联坐标系中的运动情况。

3) 建立了螺旋非圆齿轮空间啮合坐标系，将圆柱齿轮看作形成非圆齿面的刀具，找出齿轮副相对运动关系，结合共轭齿廓基本定理，最终得到了非圆齿面齿廓方程，并验证了瞬时接触状态仍为线接触。

4) 利用数学软件按照流程图编程，将得到的坐标点集绘制三维齿面，直观、准确的展现了非圆齿廓、过渡曲面的各方面信息。通过对比左右齿廓外观形状，说明非圆齿廓的相错及不对称特点，是由圆柱齿轮作轴向进给运动造成的。

[1]杨世平. 基于VB的非圆齿轮CAD/CAM系统研究与开发[J]. 机械科学与技术, 2008, 27(8): 1056-1062. YANG Shiping. Development of a non-circular gear CAD/CAM system using VB[J]. Mechanical Science and Technology for Aerospace Engineering, 2008, 27(8): 1056-1062.

[2]陈作庆, 胡松年, 翟春香, 等. 非圆行星齿轮液压马达的结构分析与研究[J]. 机床与液压, 2010, 38(23): 45-47. CHEN Zuoqing, HU Songnian, ZHAI Chunxiang, et al. The structural analysis and research of the non-circular planetary gear hydraulic motor[J]. Machine Tool & Hydraulics, 2010, 38(23): 45-47.

[3]周利锋. 一种新型摆线齿轮减速器[D]. 北京: 北京邮电大学， 2012:46-51. ZHOU Lifeng. Design of a novel cycloid gear reducer[D]. Beijing: Beijing University of Post and Telecommunications, 2012:46-51.

[4]姜虹, 王小椿. 三周节变传动比限滑差速器设计与验[J]. 农业机械学报, 2007, 38(4): 31-34. JIANG Hong, WANG Xiaochun. Research on design and working principles of three-pitch fluctuating gear ratio limited-slip differential[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(4): 31-34.

[5]马延会. 变传动比限滑差速器的齿轮设计[D].武汉: 武汉理工大学, 2007：7-16. MA Yanhui. The design of gears of variable ratio differential of slip resistance[D]. Wuhan: Wuhan University of Technology, 2007:7-16.

[6]孙良, 赵匀, 姚佳明, 等. 非匀速空间行星轮系宽窄行分插机构分析与优化[J]. 农业机械学报, 2012, 43(10): 41-71. SUN Liang, ZHAO Yun, YAO Jiaming, et al. Analysis and optimization of wide-narrow distance transplanting mechanism with spatial planetary gear train of variable speed transmission[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(10): 41-71.

[7]谭伟明, 梁燕飞, 安军, 等. 渐开线非圆齿轮的齿廓曲线数学模型[J]. 机械工程学报, 2002, 38(5): 75-79. TAN Weiming, LIANG Yanfei, AN Jun, et al. Mathematical model for tooth profile of noncircular involute gears[J]. Chinese Journal of Mechanical Engineering, 2002, 38(5): 75-79.

[8]谭伟明, 胡赤兵. 非圆齿轮滚切最简数学模型及其图形仿真[J]. 机械工程学报, 2001, 37(5): 26-29. TAN Weiming, HU Chibing. Concise mathematical model for hobbing noncircular gear and its graphic simulation[J]. Chinese Journal of Mechanical Engineering, 2001, 37(5): 26-29.

[9]李建刚, 吴序堂, 毛世民, 等. 非圆齿轮齿廓数值计算的研究[J]. 西安交通大学学报, 2005, 39(1): 75-78. LI Jiangang, WU Xutang, MAO Shimin, et al. Numerical computation of tooth profile of noncircular gear[J]. Journal of Xian Jiaotong University, 2005, 39(1): 75-78.

[10]贺敬良, 李建刚, 王准, 等. 非圆齿轮的成形砂轮展成磨削原理[J]. 农业机械学报, 2007, 38(10): 145-149. HE Jingliang, LI Jiangang, WANG Zhun, et al. Research on noncircular gear grinding method by using gear generator with form-grinding[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(10): 145-149.

[11] XIA Jiqiang, LIU Yuanyuan, GENG Chunming, et al. Non-circular bevel gear transmission with intersecting axes[J]. Journal of Mechanical Design, 2008, 130(5): 1-6.

[12]林超, 侯玉杰, 龚海, 等. 高阶变性椭圆锥齿轮传动模式设计与分析[J]. 机械工程学报, 2011, 47(13): 131-139. LIN Chao, HOU Yujie, GONG Hai, et al. Design and analysis of transmission mode for high-order deformed elliptic bevel gears[J]. Chinese Journal of Mechanical Engineering, 2011, 47(13): 131-139.

[13]林超, 聂玲, 李莎莎, 等. 偏心-高阶椭圆锥齿轮副的强度计算方法[J]. 机械工程学报, 2013, 49(5): 47-54. LIN Chao, NIE Ling, LI Shasha, et al. Strength calculation method of eccentric-high order elliptical bevel gear pair[J]. Chinese Journal of Mechanical Engineering, 2013, 49(5): 47-54.

[14]LITVIN F L, FUENTES-AZNAR A, et al. Noncircular gears design and generation[M]. New York: Cambridge University Press, 2009:9-11.

[15]沈谦. 渐开线锥形齿轮变速装置的设计原理[J]. 航空动力学报, 1993, 8(1): 75-78. SHEN Qian.Design principle of change-speed involute conical gear train[J]. Journal of Aerospace Power, 1993, 8(1): 75-78.

[16]周长秀, 沈谦. 渐开线锥形齿轮变速装置的传动与设计[J]. 机械制造, 1989(9): 9-10. ZHOU Changxiu, SHEN Qian. Design and transmission of change-speed involute conical gear train[J]. Journal of Aerospace Power Machinery, 1989(9): 9-10.

[17]LITVIN F L. Gear geometry and applied theory[M]. Prentice-Hall, 1994:105-109.

Research on meshing transmission of intersected spiral non-circular gear

SONG Hongzhou, WEI Shimin, LIAO Qizheng, GUO Lei

(Automation School, Beijing University of Post and Telecommunications, Beijing 100876, China)

In order to apply non-circular gearing to transmissions, an intersecting axis non-constant transmission ratio spiral gear pair was proposed. The spiral pitch curve of non-circular gearing was defined, and the transmission ratio equation and the conditions for pure rolling of the gear pair were found. A mathematical model for processing a non-circular tooth profile based on an inclusive method was established. By describing each section of cylindrical gear tooth surface and combining with the engagement principle of conjugate profile, the spiral gear tooth surface equations were deduced, validating that their instantaneous engagement state was line contact. The accurate non-circular gear tooth profiles were generated by numerical calculation software. The characteristics of left and right non-circular gear tooth profiles were analyzed, providing a theoretical basis for further research and application.

gear; spiral non-circular gear; intersected axes; engagement principle; tooth profile; line contact

2014-04-03.

时间：2015-08-24.

国家863计划基金资助项目(2011AA040203)；国家科技支撑计划基金资助项目(2013BAD17B06)；粮食公益性行业科研专项基金资助项目(201313009-06).

宋洪舟(1988-), 男, 博士研究生； 魏世民(1965-), 男, 教授,博士生导师.

魏世民，E-mail：wsmly@bupt.edu.cn.

10.3969/jheu.201404012

TH132.4

A

1006-7043(2015)09-1223-06

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20150824.1620.003.html