新型轴流导叶可调液力变矩器设计与分析

, ,

(吉林大学 机械科学与工程学院， 吉林 长春　130022)

引言

作为能源消耗的大户，装载机、推土机等铲土运输机械如何提高整机性能并实现节能受到越来越广泛的关注[1]。对于工程车辆而言，动力传动系统中零部件自身性能及各部件之间匹配性能的改善将有助于整机性能的提高，尤其是发动机与液力变矩器间的匹配问题[2-4]。由于作业工况的复杂化，传统液力变矩器固定不变的能容特性无法同时满足工程机械各阶段作业的需求，因此通过设计能容可变的新型液力变矩器，实现与发动机之间的动态匹配是目前解决这一问题的有效手段之一[5]。

常见的导叶可调液力变矩器为长方形循环圆径流导叶可调液力变矩器[6]，然而对于铲土运输机械而言，由于空间结构尺寸、液力变矩器透穿性能等因素的影响，想要保证液力变矩器透穿性能不变的同时，将长方形循环圆径流导叶可调液力变矩器应用于铲土运输机械比较困难。基于此，轴流导叶可调液力变矩器的研究不仅具有重要的工程实际意义，而且其对于工程机械面向节能化产品的发展具有重要的作用。

1　循环圆、叶片与结构设计

本研究所设计的新型轴流导叶可调液力变矩器与普通的向心涡轮液力变矩器尺寸相当，因此选取装载机、推土机等铲土运输机械常用的系列化尺寸370 mm作为循环圆的有效直径。在设计循环圆的过程中，考虑到导轮叶片为可调叶片，因此为了实现导轮叶片的转动，采用“两圆弧+直线”的设计方法设计新型变矩器的循环圆[7]，如图1所示。由图可知，新型变矩器与普通变矩器的循环圆在导轮处的形状明显有所不同。

叶片理论设计方法主要包括环量分配法和等倾角射影法[5]。本研究通过等倾角射影法对新型轴流导叶可调变矩器叶片进行优化设计[8，9]。得到的新型变矩器的泵轮叶片和涡轮叶片如图2所示。

图1　新型变矩器循环圆

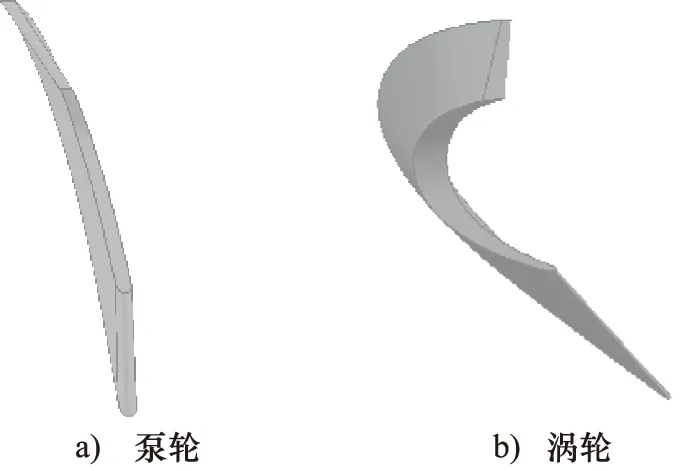
图2　泵轮和涡轮叶片

与普通变矩器相比，新型变矩器导轮的安装位置虽然相同，但其导轮的叶片需要进行转动。因此为了实现导轮叶片在导轮内的转动，导轮的叶片将不再是扭曲的三维叶片，而设计为圆柱形叶片。同时为了充分利用有限的空间结构，提高新型变矩器的性能，叶片内环的长度大于外环，如图3所示。

图4为新型变矩器的总体结构。从总体结构可知，与普通向心涡轮液力变矩器相比，新型变矩器的不同之处主要在于导轮叶片、导轮座和导叶调节机构。当工作介质流经导轮时，通过导叶调节机构旋转导轮叶片，可以改变液力变矩器的能容性能。可见，新型变矩器设计的成功与否不仅取决于叶片设计， 导叶调节机构的设计同样也是关键的环节。

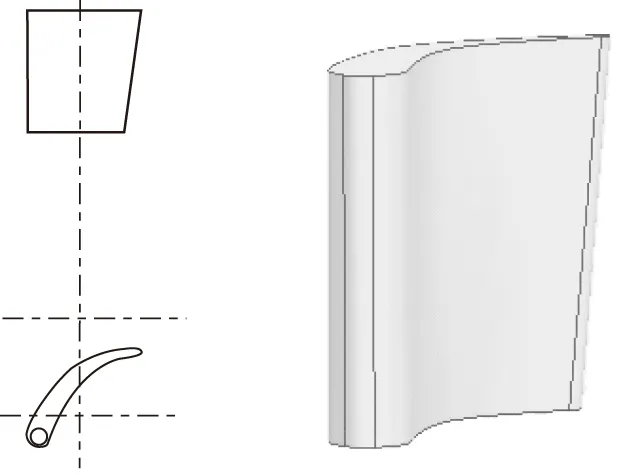
图3　导轮叶形和叶片

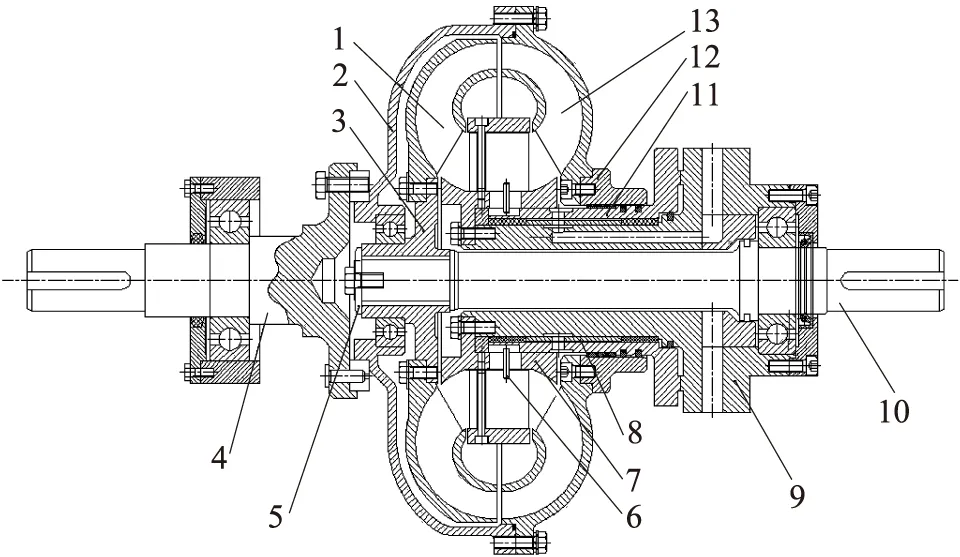
1.涡轮　2.驱动轮　3.涡轮毂　4.输入轴　5.压盖　6.拨动轴7.导轮　8.隔套　9.导轮座　10.输出轴　11.调节轴12.泵轮座　13.泵轮图4　新型轴流导叶可调液力变矩器总体结构

2　导叶调节机构设计

由于新型变矩器通过转动导轮叶片来实现变矩器能容的无级调节，因此如何实现导轮叶片的转动不仅至关重要，而且是设计能否成功的关键。图5为新型变矩器导轮座组件。如图所示，与普通变矩器的结构不同，导轮叶片上不仅装有叶片绕其转动的转动轴7，而且在叶片外环上还装有拨动轴5。除此之外，导轮座和导轮外环之间装有调节轴4， 导轮叶片正是通过转动调节轴进而带动拨动轴拨动叶片绕着转动轴来实现导叶开度的变化，调节轴的转动可以通过手动或电动(自动)实现。

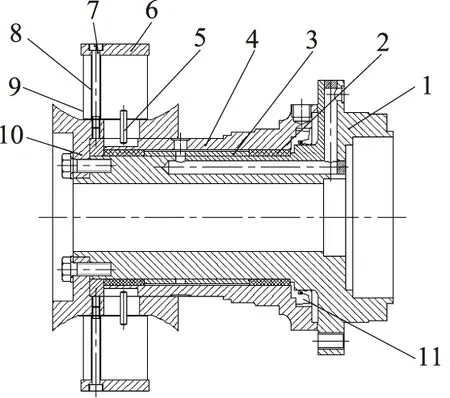
1.导轮座　2.滑动轴承　3.隔套　4.调节轴　5.拨动轴　6.内环7.转动轴　8.轴套　9.导轮叶片　10.外环　11.骨架油封图5　轴流导叶可调液力变矩器导轮座组件

图6和图7为导轮的内环和外环结构。通过导轮的内外环结构，则可以更清楚地了解导轮叶片实现转动的过程。从图6的内环结构可知，与导轮叶片内环相接触的表面为多边形结构，以便于导轮叶片的旋转。从图7的外环结构可知，与导轮叶片外环相接触的表面不仅同样为多边形结构，而且在其表面上还开有圆弧状的凹槽，主要用于拨动轴的移动。

图6　内环结构

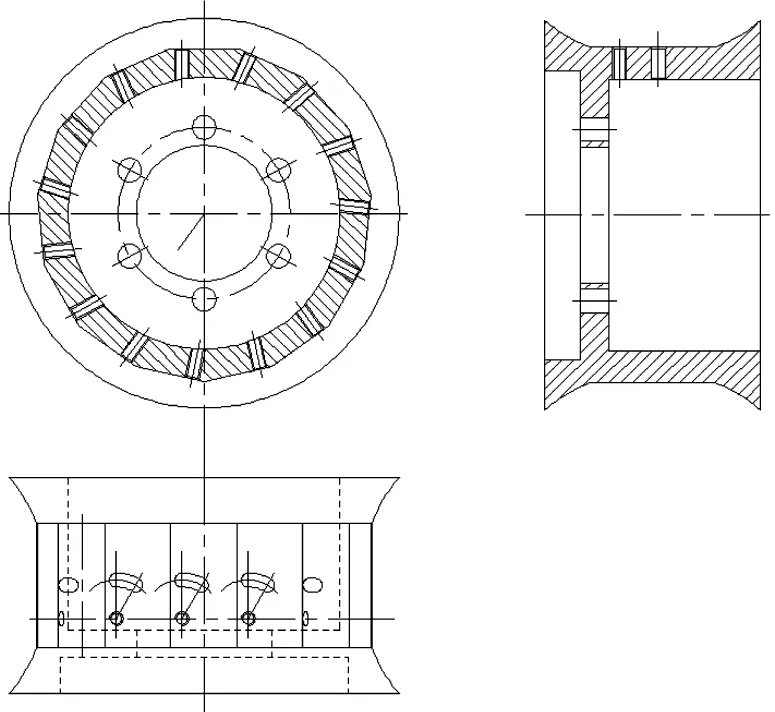
图7　外环结构

为了更加清楚的表达导轮叶片角度的变化，对导轮叶片转动位置(开度)进行定义，如图8a所示，将导轮叶片由最大开度位置转至最小开度位置的角度定义为θ，将θ进行等分后的角度为θx(x=0、1、2……)，定义导轮叶片转动开度为k，则：

(1)

图8b为k=0、k=0.5、k=1时导轮叶片开度变化的三维图。虽然导轮叶片只能转动20°，但其能容特性的连续变化范围已然能够满足动态匹配的要求。

3　轴流导叶可调变矩器性能预测

3.1　轴流导叶可调液力变矩器CFD计算

随着计算机技术的发展和CFD (计算流体动力学)技术的日益成熟，对复杂流动工程问题的三维、非定常、不可压缩粘性流体的流动分析已经可以采用CFD软件加以解决[10]。运用CFD对液力变矩器进行仿真计算已经成为一种常规的技术手段。许多实验数据都已表明，向心涡轮液力变矩器的CFD特性计算结果与台架试验的结果非常接近，在设计阶段进行理论分析时，可以采用CFD计算的结果作为依据[11-14]。基于此，本研究采用CFD计算方法对新型变矩器进行仿真计算，计算流程如图9所示。

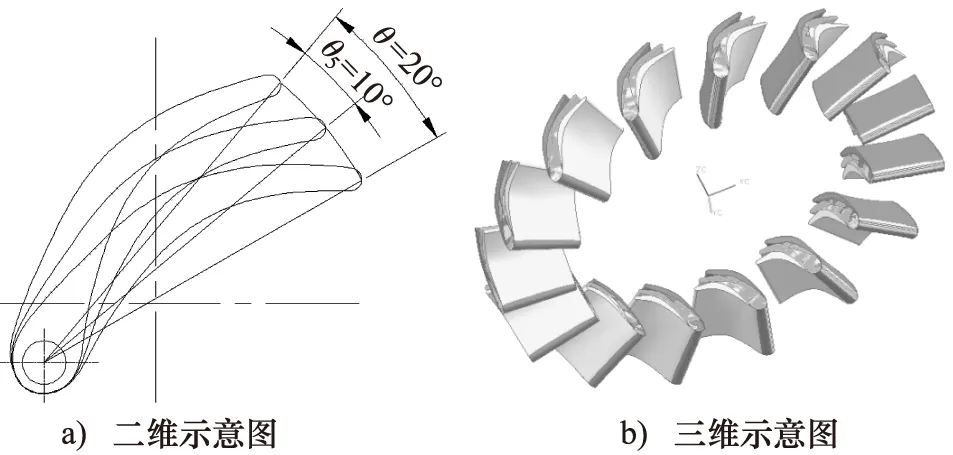
图8　导轮叶片开度

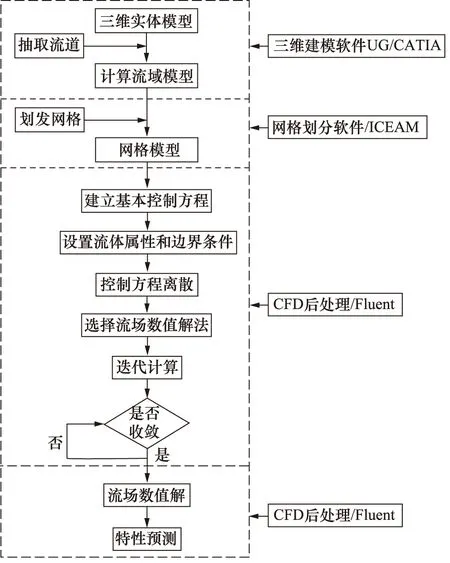
图9　CFD数值模拟计算流程

将前述设计的循环圆和叶片导入三维软件UG中进行流道抽取，图10分别为泵轮、涡轮以及导轮(k=0.5)下流道模型，将各叶轮流道模型构成一个整体作为计算域模型。

图10　三维流道模型

将所得到的流道模型导入ANSYS/ICEAM中进行网格划分。由于网格质量的高低对计算结果的精度有很大的影响，因此选用六面体结构化网格对其进行网格划分，并对结构复杂处进行网格加密，得到泵轮、涡轮以及导轮(k=0.5)的网格结构如图11所示。

图11　网格模型

将网格模型生成CASE文件导入FLUENT中，湍流模型选择大涡模拟(LES)，压力速度耦合算法选择SIMPLE，离散格式选取二阶迎风格式。泵轮转速设置为2000 r/min，各叶轮进出口设置为滑移网格，其余边界条件设置为壁面条件(wall)。工作介质采用液力传动油，密度为833.2 kg/m3，动力黏度为0.009865 Pa·s。为了提高计算精度，按变矩器的实际工作液体平均温度范围，设定油温为84 ℃。对计算结果进行后处理即可得到新型变矩器的相关特性。

3.2　轴流导叶可调液力变矩器特性分析

通过CFD计算可以得到各叶轮的转矩值，即轴流导叶可调液力变矩器的外特性和原始特性。轴流导叶可调液力变矩器的原始特性不仅与转速比i有关，同时随着导叶开度k的变化而变化。原始特性的各项性能指标均可以看成是转速比i和导叶开度k的函数。为了更好的体现轴流导叶可调液力变矩器的特性，在进行CFD计算时，导叶开度k在0～1每隔0.1取值，转速比i在0～1每隔0.1取值。由计算得到的各叶轮转矩值可以得到轴流导叶可调液力变矩器的原始特性，并用以转速比i和导叶开度k为横坐标的曲面来表达，如图12所示。

通过图12可以发现，随着转速比i和导叶开度k的改变，变矩比K、效率η和泵轮转矩系数λB(能容)的数值都会发生相应的变化。每一个导叶开度下，都会有相应的原始特性与之对应，可以认为新型变矩器的特性是由不同开度下的多组液力变矩器的特性共同组成。

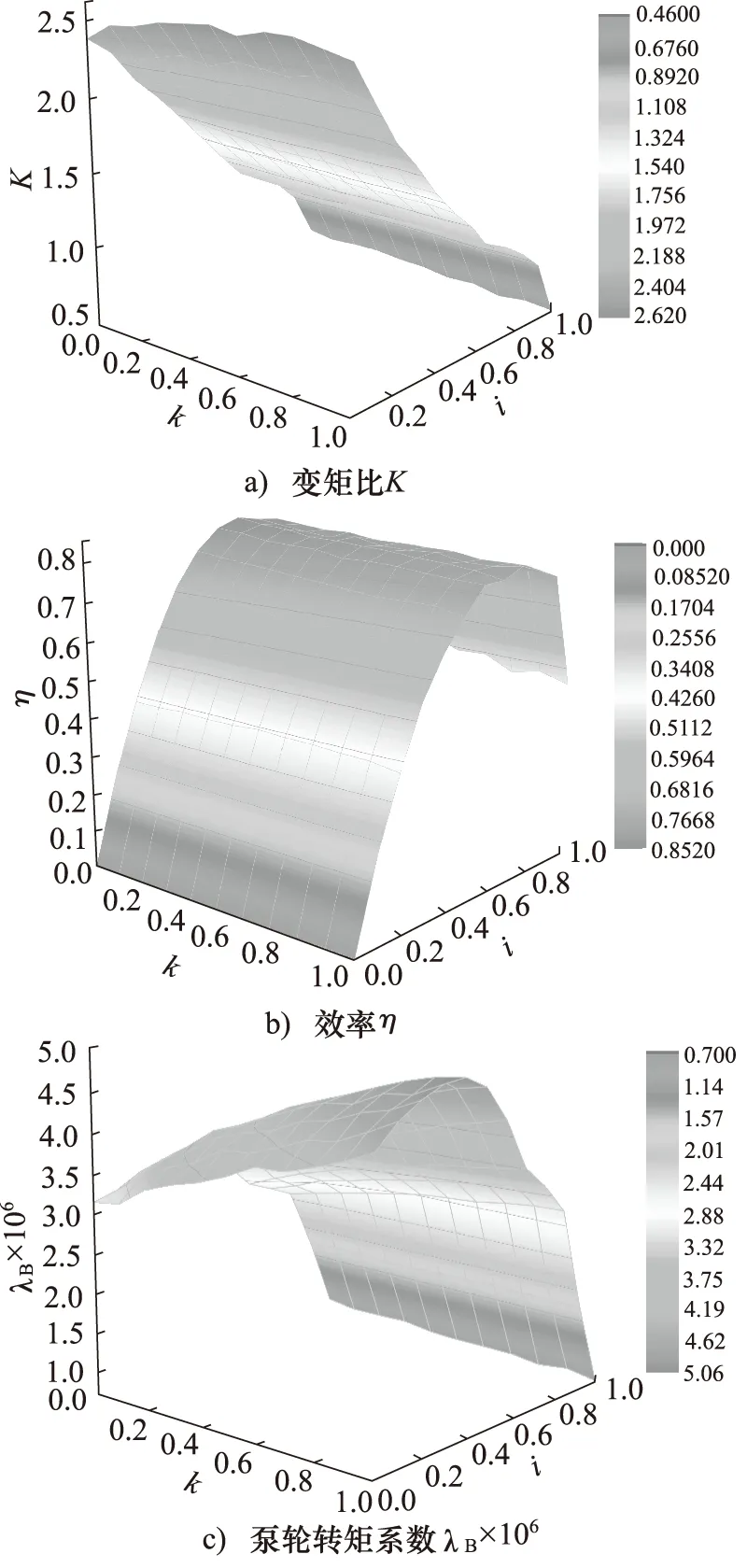
图12　新型轴流导叶可调液力变矩器原始特性

为了更直观的表述不同开度下新型变矩器的特性，现分别用导叶开度k=0、k=0.3、k=0.5、k=0.7、k=1的各平面与图12所示的曲面相交，分别获得导叶开度k=0、k=0.3、k=0.5、k=0.7、k=1下的新型变矩器的原始特性曲线，如图13所示。由图13a可以看出，随着导叶开度的变化，失速变矩比K0(i=0)在2.39～2.62之间变化；在i=0以外其他工况，随着导叶开度的增大，变矩比的变化趋势为略有下降。由图13b可以知道，在高效范围内效率值会随着导叶开度k的增大略有降低，设计工况(i=0.7)下的最高效率值的变化范围介于80.63%～85.05%之间。由图13c可知，泵轮转矩系数λB(能容)的变化较为明显，随着导叶开度k的变化呈现一定的规律性。导叶开度k增大的同时泵轮转矩系数λB(能容)逐渐增加。由此可见，通过调节导叶开度可以实现新型变矩器能容的连续变化。正是基于此种特性，当与发动机进行匹配时，泵轮的转矩特性会随着导叶开度的调节不断变化，从而实现一种动态的匹配，根据作业工况的需求匹配到动力性或经济性的最佳点，进而提高整机的性能。

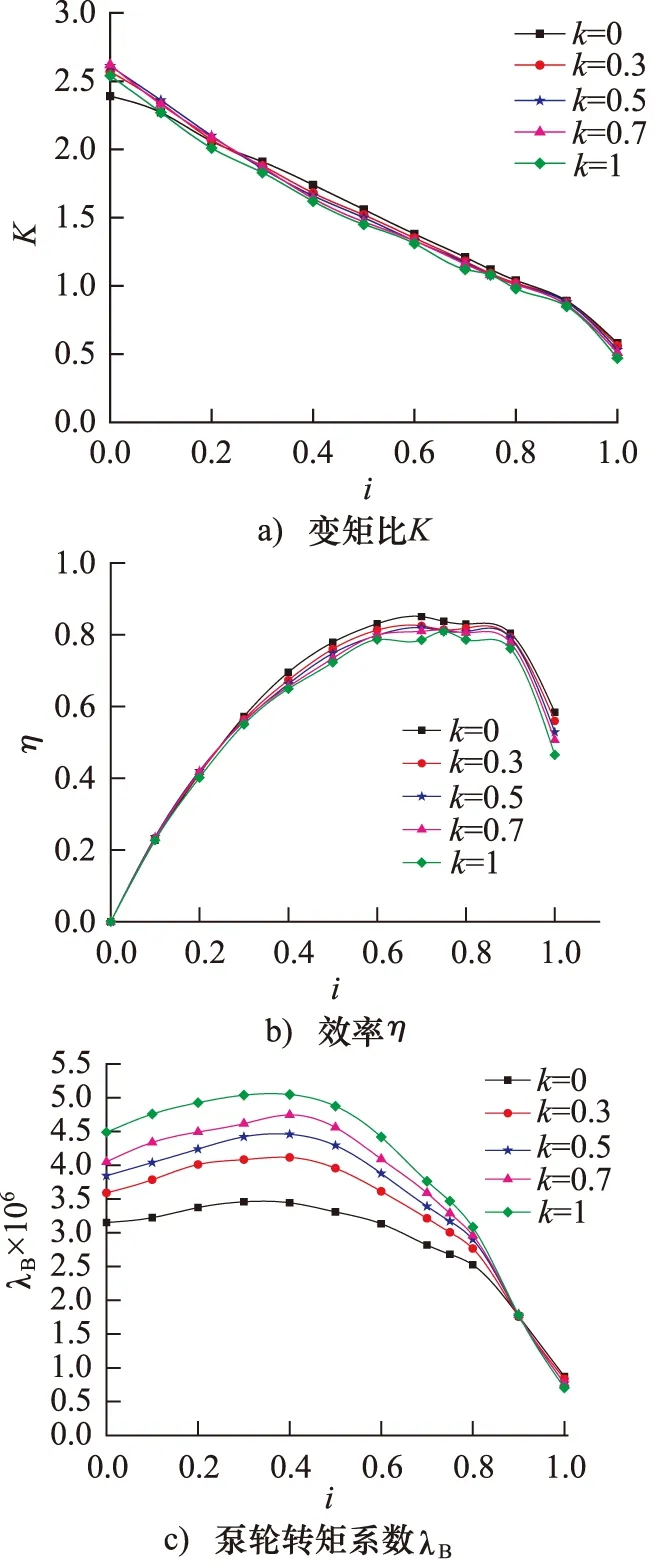
图13　不同导叶开度下新型变矩器原始特性

4　结论

(1) 采用“两圆弧+直线”的设计方法设计了有效直径370 mm的新型轴流导叶可调液力变矩器循环圆。运用等倾角射影法设计了新型变矩器的各叶轮叶片的叶型，并给出了其总体结构；

(2) 设计了导叶调节机构，实现了新型变矩器导轮叶片的转动。并根据导叶旋转的位置定义了导叶开度的变化范围；

(3) 运用CFD技术对不同开度和不同转速比下的新型轴流导叶可调液力变矩器进行数值模拟计算，得到了新型变矩器的原始特性。通过对其原始特性进行分析可知，新型变矩器能容特性随着导叶开度k和转速比i的变化而变化，通过调节导叶开度可以实现新型变矩器能容的连续可控性，其应用于工程机械能够实现与发动机的动态匹配，提高整机性能。

参考文献：

[1]张大庆.工程机械节能环保研发趋势[J].建筑机械化,2015,(6):27-30.

[2]刘钊，张旭晨，王磊.发动机与液力变矩器功率匹配优化[J].中国工程机械学报，2014，12(6)：536-539．

[3]Sun Wei, Ma Bing, Ma Jin, et al. Dynamic Matching Analysis of Engine and Torque Converter in Tracked Coach Car[C]//Advances in Manufacturing Science and Engineering V, 2014:314-318.

[4]马文星.液力传动理论与设计[M].北京：化学工业出版社，2004．

[5]马文星,王若仰,才委.导叶可调式液力变矩器导轮特性研究[J].华南理工大学学报(自然科学版),2014,(12):84-89.

[6]陆建芳.一种三圆弧逼近方法[J].浙江工业大学学报,1997,(3):236-241.

[7]马文星，刘春宝，雷雨龙，等.工程机械液力变矩器现代设计方法及应用[J].液压气动与密封，2012，32(10):71-76.

[8]雷雨龙，葛安林，田华，等．基于内流场分析的液力变矩器改型设计[J]．机械工程学报，2006，42(2)：125-128．

[9]Guangqiang W, Peng Y. System for Torque Converter Design and Analysis Based on CAD/CFD Integrated Platform[J]. Chinese Journal of Mechanical Engineering, 2008, 21(4).

[10]吴光强，王立军.基于CFD的液力变矩器等效参数性能预测模型[J]．同济大学学报:自然科学版,2013,41(1):121-127．

[11]罗虹，王腾腾，李兴泉，等．液力变矩器性能参数的计算误差及其修正方法[J]．西南交通大学学报，2012，47(3)：471-476．

[12]Watanabe N, Miyamoto S, Kuba M, et al. The CFD Application for Efficient Designing in the Automotive Engineering [R]. SAE Technical Paper, 2003.

[13]韩克非，吴光强，王欢．基于CFD的泵轮叶栅关键参数对液力变矩器的性能影响预测[J]．汽车工程，2010，32(6)：497-501．

[14]严鹏，吴光强．液力变矩器性能分析[J]．同济大学学报:自然科学版，2004，32(11)：1504-1507．