群G 的模糊子群与正规模糊子群①

马斌斌，桑小双

(安徽大学数学科学学院，安徽 合肥230601)

0 引 言

自从1965 年Zadeh［1］提出模糊集［2～3］的概念以来，模糊概念作为普通概念的推广便逐渐引入了数学的各个分支，群［4］随之也被模糊化，模糊集和系统理论［5］得到了快速的发展.1971 年Rosenfeld［6］引入了模糊群的概念，由此开创了模糊代数的研究领域;1982 年刘旺金［7］提出了模糊正规子群等一些概念，并讨论了有关性质.随后，许多学者对模糊子群的代数性质进行了系统的研究［8～9］.1990 年Biswas R［10］提出来反模糊子群的概念，进一步拓宽了模糊代数学的研究领域，之后不少学者对反模糊子群进行了深入且有意义的研究［11～14］，得到了一系列的研究成果.

在上述研究的基础上，从代数的角度引入了模糊子群的左陪集和右陪集，证明了左右陪集之间存在双射，进一步刻画了模糊子群，并对模糊子群的若干性质进行了探讨.

1 预备知识

定义1.1［4］: 一个非空集合G 对于一个叫做乘法的代数运算◦来说作成一个群，假如

(1)G 对于乘法来说封闭:∀x，y ∈G，x ◦y ∈G;

(2)结合律成立∀x，y，z ∈G，x ◦(y ◦z)=(x◦y)◦z;

(3)对于∀x ∈G，G 中至少存在一个单位元e，使得e ◦x=x ◦e=x 成立;

(4)对于∀x ∈G，G 中至少存在一个单位元x－1，使得x－1◦x=x ◦x－1=e 成立.

定义1.2［4］: 设H 为G 的一个子群，x ∈G，则称群G 的子集xH={xh/h ∈H}为群G 关于子群H 的一个左陪集，而称Hx={hx/h ∈H}为群G 关于子群H 的一个右陪集.

定义1.3［4］: 设H 是群G 的一个子群，如果对G 中每个元素x 都有xN=Nx 即xNx－1=N，称N 是群G 的一个正规子群.

2 模糊子群

上面介绍了经典集合中的子群，陪集，正规子群的定义，性质及定理，下面将过渡到模糊子集中.在讨论模糊子群前，先介绍λ－截集.

定义2.1［3］: 设X 为一论域，F(X)为X 上的模糊子集的全体，A ∈F(X)，对于∀λ ∈［0，1］，Aλ={x ∈X/A(x)≥λ}称为A 的λ－截集.

定义2.2［1］: 设G 为一个群，A ∈F(G)，如果∀x，y ∈G，满足下列条件

则称A 为G 的一个模糊子群，因此G 的性质同样适用于A.

定理2.1［1］: 群G 的模糊子集A 为G 群的一个模糊子群当且仅当

定理2.2: 群G 的模糊子集A 为群G 的一个模糊子群的充要条件是Aλ为群G 的一个子群.

证明:(⇒)(1)∀x，y ∈Aλ，可得A(x)≥λ，A(y)≥λ，又A 为群G 的一个模糊子群，有A(xy)≥A(x)∧A(y)≥λ，故xy ∈Aλ.

(2)∀x ∈Aλ，由A 为群G 的一个模糊子群可得A(x－1)≥A(x)≥λ，于是x－1∈Aλ综上可得A为群G 的一个子群.

(⇐)由Aλ={x ∈X/A(x)≥λ}知，若x ∈Aλ，则A(x)≥λ，从而A(x)=∨{λ/x ∈Aλ}，故A(xy)=∨{λ/xy ∈Aλ}≥∨{λ/A(x)≥λ，A(y)≥λ}=A(x)∧A(y);A(x－1)=∨{λ/x－1∈Aλ}≥∨{λ/x ∈Aλ}=∨{λ/A(x)≥λ}=A(x)

综上可得A 为群G 的一个模糊子群.

3 正规模糊子群

定义3.1: 设A 为群G 的一个模糊子集，对于∀x ∈G，则称xA，Ax 也为群G 的模糊子集，且对∀y ∈G，有(xA)y = A(x－1y)，(Ax)(y)=A(yx－1).

定义3.2: 设G 为一个群，A 为群G 的一个模糊子群，对于∀x ∈G，则称xA 为模糊子群A 的一个左陪集，同理称Ax 为模糊子群A 的一个右陪集，且对∀y ∈G，有(xA)y =A(x－1y)，(Ax)(y)=A(yx－1).

可以看出，一般情况下，一个模糊子群A 的左右陪集不相等，接下来我们将要讨论模糊子群A 的陪集的性质.

定理3.1: 设A 为群的G 一个模糊子群，对于∀y ∈G，则

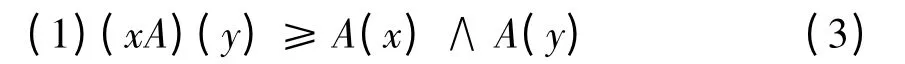
(2)(Ax)(y)≥A(x)∧A(y).

证明:(1)(xA)y = A(x－1y)≥A(x－1)∧A(y)，又A(x－1)≥A(x)，所以A(x－1)∧A(y)≥A(x)∧A(y)，从而有(xA)(y)≥A(x)∧A(y).

(2)同理可证(Ax)(y)≥A(x)∧A(y).

定理3.2: 设A 为群的G 一个模糊子群，令M={xA/x ∈G}，N={Ax/x ∈G}，则M 与N 之间存在一个双射，从而模糊子群A 的左右陪集的个数或者无限或者有限且个数相等.

证明: 在M 与N 之间存在一个映射f:M →N，xA →Ax 显然为一个映射.

(2)对于∀x ∈G，A 的一个右陪集Ax 都有一个左陪集xA 与之对应，所以f 为满射，综上的f 为双射.

定义3.3: 设A 为群G 的一个模糊子群，∀x∈G，若有Ax=xA，则称A 为群G 的一个正规模糊子群.

定理3.3: 若群G 为一交换群，则群G 的任一模糊子群都是G 的正规模糊子群.

证明: 设A 为群G 的一个模糊子群，∀x ∈G，则称xA 为模糊子群A 的一个模糊子集，故∀y ∈G，有(xA)(y)=A(x－1y)，又群G 为一交换群，故x－1y=yx－1，从而(xA)(y)=A(x－1y)=A(yx－1)=(Ax)(y)，由y 的任意性得Ax=xA，故模糊子群A 为G 的正规模糊子群.

证明:(⇒)设A 为群G 的一个模糊子群，有xA=Ax(∀x ∈G)，于是

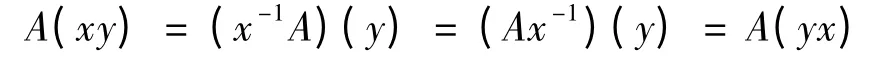
(⇐)由已知A(xy)=A(yz)(∀x，y ∈G)得A(x－1y)=A(yx－1)，从而对∀y ∈G，有(xA)(y)=A(x－1y)=A(yx－1)=(Ax)(y)，由y 的任意性得xA=Ax(∀x ∈G)，即A 为群G 的正规模糊子群.

定理3.5: 群G 的模糊子群A 为群G 的正规模糊子群的充要条件是

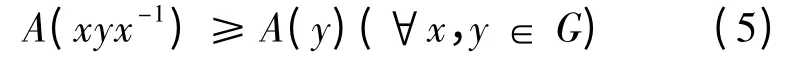
证明:(⇒)由定理3.4 和子群对结合律成立得

(⇐)已知A(xyx－1)≥A(y)(∀x，y ∈G)，则

同理可证(Ax)(y)≥(xA)(y)，故(Ax)(y)=(xA)(y)(∀y ∈G)，从而xA=Ax(∀x ∈G)，即A为群G 的正规模糊子群.

定理3.6: 群G 的模糊子群A 为群G 的正规模糊子群的充要条件是

证明:(⇒)A 为群G 的一个模糊子群，对于∀y ∈G，(xAx－1)(y)=(Axx－1)(y)=A(y)，由y的任意性得xAx－1=A，当然有xAx－1⊆A(∀x ∈G).

(⇐)已知∀x ∈G，有xAx－1⊆A，则∀y ∈G，(xAx－1)(yx－1)≤A(yx－1)，即(xAx－1x)(y)≤(Ax)(y)，因此(xA)≤(Ax)，从而由Y 的任意性得xA ⊆Ax，同理可证xA ⊇Ax.

高校行政权力和学术权力在运行机制方面的问题其主要表现：决策机制方面，各学术权力机构在实际运行中的教授治学氛围不浓，民主程度有待提高，行政权力在决策中发挥主导作用；运行机制方面，行政权力主导学术权力，虽基本上都成立了校学术委员会，但教学委员会等发展不充分，其运行机制难以发挥作用，学术权力运行受限；监督机制方面：普通老师参与不足，各高校对学术权力机构的设置随意性大。事实上高校学术权力和行政权力之间确实存在着冲突与矛盾，但是通过建立有效的机制和保障措施，最终学术权力和行政权力可以协调发展。

综上可得A 为群G 的正规模糊子群.

综合上面介绍的几个关于正规模糊子群的定理可得一下命题成立.

命题3.1:A 为群G 的一个模糊子群，则下列条件是等价的

(1)A 为群G 的正规模糊子群;

(2)A(xy)=A(yx)(∀x，y ∈G);

(3)Ax=xA(∀x ∈G); (7)

(4)A(xyx－1)≥A(y)(∀x，y ∈G);

(5)xAx－1⊆A(∀x ∈G).

［1］ Zadeh A.Fuzzy Sets［J］.Information and Control，1965(8):338－353.

［2］ 罗承中.模糊集与集合套［J］.模糊数学，1997，20(2):20－22.

［3］ 李敏.直觉模糊集的截集［J］.辽宁师范大学学报(自然科学版)，2007，30(2):152－154.

［4］ 张禾瑞.近世代数［M］.北京:高等教育出版社，2010.

［5］ 张振良.模糊集理论与方法［M］.武汉:武汉大学出版社，2010.

［6］ Rosenfeld A.Fuzzy Subgroups［J］.Math.Anal.1971，35:512－519.

［7］ 何天荣.模糊正规子群的若干性质研究［J］.数学学习与研究，2013.17.

［8］ 吴望名.正规模糊子群［J］.模糊数学，1981，(1):21－30.

［9］ 朱楠德.生成Fuzzy 子群［J］.模糊系统与数学，1989，3(2):24－31.

［10］ 李文婷，辛小龙.模糊子群的T－正规模糊软群［J］.西北大学学报(自然科学版)，2014，03－0355－05.

［11］ 杨家辉，刘龙章.生成反模糊子群［J］.大学数学，2008，24(5):113－116.

［12］ 王盛海.群的反模糊子群［J］.模糊系统与数学，2005，19(2):58－60.

［13］ 刘金良，闫瑞霞，姚炳学.关于反模糊子群的若干性质［J］.青岛科技大学学报，2006，27(6):549－556.

［14］ 刘金良，闫瑞霞，姚炳学.关于反模糊子群的反模糊正规子群［J］.聊城大学学报(自然科学版)，2007，20(2):1－3.