基于滑模变结构的Vienna整流器新型双闭环控制策略研究

马 辉 谢运祥

基于滑模变结构的Vienna整流器新型双闭环控制策略研究

马 辉 谢运祥

（华南理工大学电力学院 广东省 广州市 510641）

传统电流电压双闭环控制策略的PI调节器控制参数为常数且较为敏感，在系统启动和负载变动时，Vienna整流器存在动态响应速度慢、抗干扰性能差、网侧电流谐波（THD）含量大等问题。为此，提出新型双闭环滑模非线性控制策略来提高输出直流侧电压和输入交流侧电流的动态响应速度以及抗干扰性能，其中内环采用无需dp旋转坐标变换的滑模直接功率控制（SMC-DPC）；外环采用电压平方反馈闭环的滑模控制；详细推导该算法，给出具体设计过程。最后利用仿真和实验对新型双闭环滑模非线性控制策略与传统双闭环PI控制方案进行比较，结果表明：前者明显优于后者，在启动和负载变化时表现出良好的动态性能和鲁棒性能。

Vienna整流器 滑模变结构 双闭环控制 直接功率控制 电压平方

1 引言

滑模控制（Sliding Mode Control，SMC）是一种不连续的非线性控制，在预先设计的滑模面上快速地切换系统的控制状态，具有高频开关特性，特别适用于电力电子装置的开关控制[1-6]。另外，SMC对系统模型精度要求不高，对参数变化和外部扰动不敏感，具有动态响应速度快、抗干扰能力强、控制规律简单和实现容易等优点[4,6]。基于上述优点，近年来已有大量文献将其应用在三相PWM整流器的控制系统设计中。

三相三电平PWM整流器的佼佼者:三相Vienna整流器，因其开关数目少电路结构简单、无输出电压桥臂直通、无需设置开关死区、输入电流谐波含量低、可实现输入单位功率因数校正等优点，受到各国学者的广泛关注[7-16]。对Vienna整流器的研究主要集中在数学模型分析、优化脉宽调制技术和改善电路性能的控制策略等三方面。其中，文献[7-9]分析该拓扑的大、小信号数学模型，设计PI控制器。文献[10]中电压外环采用PI调节器，电流内环采用改进滞环控制算法，虽结构简单但开关频率不固定导致电路参数设计困难。文献[11-13]基于电压电流双闭环PI控制引入空间矢量调制（SVPWM）解决了开关频率不固定的问题，而文献着重分析适合Vienna整流器的简化等效SVPWM方法。文献[14]采用优化电流PI调节器的矢量控制，满足宽输入电压和变电感量条件下整流器的稳定性能要求，没有考虑电路的动态性能。为改善整流系统控制精度和稳定性，文献[15-16]采用单周期非线性控制，主要研究占空比收敛和电压外环补偿网络；对电压外环非线性问题未做进一步考虑。随着Vienna整流器应用场合的多样化，对其静、动态性能的要求也越来越高，由于该整流器是一个非线性系统，采用常规的双闭环PI控制算法难以达到理想的控制效果。

滑模变结构控制是解决非线性系统控制问题的重要方法之一，已有大量文献将滑模控制成功应用在三相变换器的外环控制方法中[1-2]，而文献[2]、[5]和[17]将其应用在并网逆变器和两电平整流器的内环。为此，本文将滑模控制应到Vienna整流器的双闭环中，提出新型双闭环滑模非线性控制策略，内环采用直接功率滑模控制（DPC-SMC），不需要电网电压的相位信息和同步旋转坐标变换，具有控制结构简单，计算量小和动态响应快等优点；电压外环采用电压平方反馈闭环滑模控制器提高电压响应速度，并分析电压外环的非线性。详细推导该策略的设计过程，包括建立系统的滑模变结构模型，选择滑模面，给出滑动模态的可达条件和控制率等。最后，利用仿真和实验与传统双闭环PI控制进行对比分析，结果表明:上述控制策略改善了系统的动态性能和鲁棒性能，更具优越性。

2 Vienna整流器的功率数学模型

图1为三相Vienna整流器的主电路拓扑结构，ea、eb、ec为三相交流电源；ia、ib、ic为三相输入电流；ip、in为直流母线正向和负向电流；La、Lb、Lc为三相滤波电感，其值为L；Ra、Rb、Rc为三相滤波电阻，其值为R；Cp、Cn为直流侧上下电容，其值为C；直流母线电压vdc=vcp+vcn，vcp、vcn(vcn=vcp)分别为上下直流电容的电压；RL为输出电阻负载；为Sabc三相的开关函数，每个双向开关由一个开关功率器件和四个二极管组成，结构如图1右半部所示；每只桥臂上存在上下两只快速恢复二极管（a相:Dap、Dn）。

图1 三相Vienna整流器的拓扑结构Fig.1 Topological structure of three-phase Vienna rectifier

电网处于理想平衡状态，整流器工作在连续电流模式下，根据其工作过程，可得到abc坐标系下的数学模型:

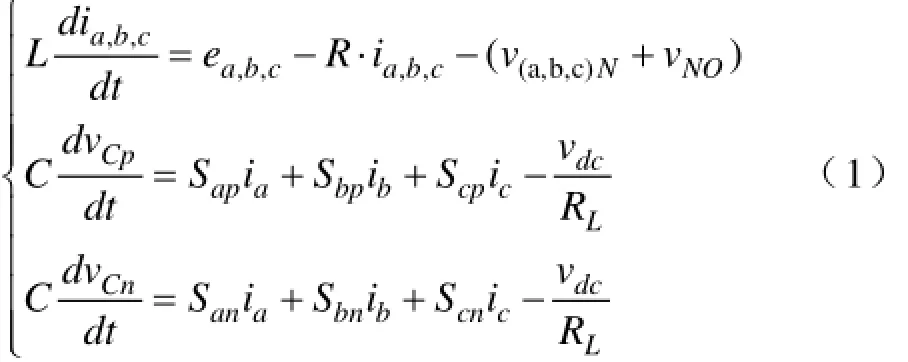
其中Sip、Si（ni=a,b,c）分别为正方向电流和负方向电流的开关函数；利用等功率变换矩阵，将三相静止坐标系下的数学模型转换到两相静止α-β坐标系下，如式（2）所示。

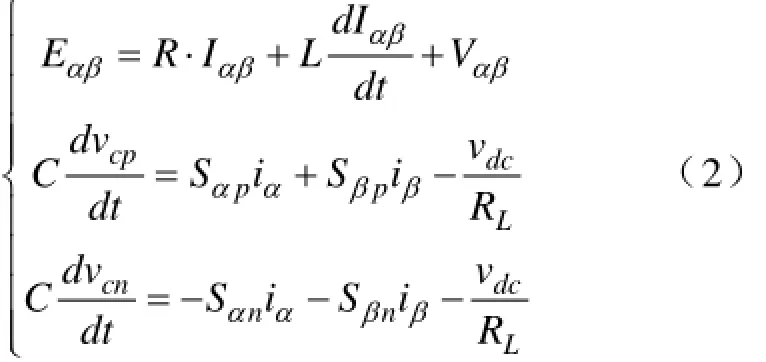
式中，Eαβ、Iαβ分别为电网电压和输入电流的α、β轴分量，L、R分别为输入电感和电阻，ω为交流电源的角频率，由式（2）得到α-β坐标系下的等效电路模型，如图2所示。

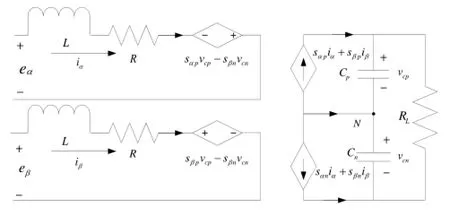
图2 α-β坐标系下的等效电路模型Fig.2 The equivalent circuit model in the α-βframe

根据瞬时功率理论，求得在两相静止α-β坐标系下的瞬时功率:

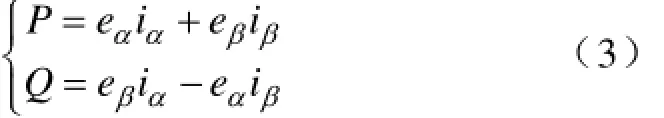
理想电源电压在两相静止坐标系下满足:

不考虑电网谐波，忽略交流侧电抗器的阻值，从静止坐标系下的数学功率模型入手，来分析交流侧瞬时功率的变化，对式子（3）求导，并将式（2）和（4）代入，求得瞬时功率的微分方程:

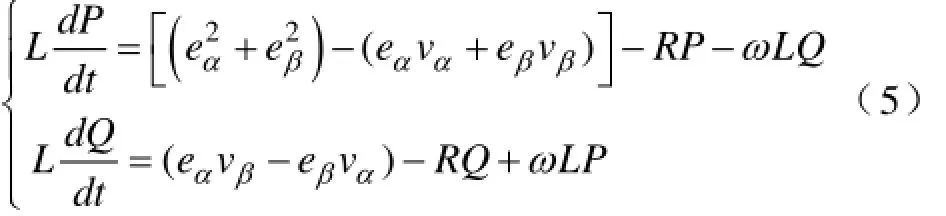
为分析直流侧功率流动，将式子（2）中直流侧数学等式两端同乘以vdc，同时等式两端分别相加，并用vdc/2替换vcp、vcn，得到直流侧功率模型:

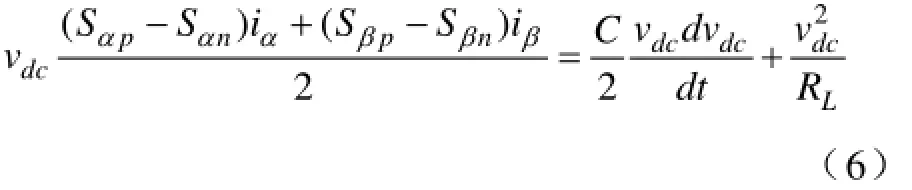
有功功率单方向从交流侧流到直流侧，等式（6）左端的式子是联系交流侧和直流侧的一个纽带，不计电路中的损耗（电路等效阻抗损耗和开关损耗），交流侧输入功率与直流侧吸收功率相等，则得到:式中，有功功率为两个直流电容储存能量与负载能量之和，Pac为交流输入功率，Pdc为直流侧功率，为直流侧上下两个电容的瞬时功率，R为负载瞬时功率。L

基于上述分析可知:有功功率单方向从交流侧流到直流侧，而无功功率仅在交流侧流动，两者的耦合关系通过交流电感体现；直流电容在一个开关周期内不消耗功率，只提供稳定直流电压的作用；有功功率由直流电压的数值平方体现，电压外环的输出作为功率内环的有功给定值，无功给定值设定为零，式（5）-（7）所描述的数学模型为设计滑模控制器奠定基础。

3 新型双闭环控制系统

基于滑模变结构的双闭环控制系统有两个控制目标:

（1）直流输出电压vdc能够快速地跟随给定电压，不受负载电流iL变化的影响，输出稳定的直流电压。

（2）交流侧输入电流为正弦，谐波含量低于3%；网侧输入功率因数为单位功率因数，即功率内环对网侧输入无功功率的控制为零，使整流器工作在单位功率因数状态下。

上述两个控制目标可视为两个相对独立的给定运动跟踪问题，本文通过设计两个滑模控制器I、II组成双闭环控制系统实现对输入电流和输出直流电压的稳定控制。

3.1功率内环滑模控制器的设计

3.1.1 滑模面的选择

滑模变结构控制器是为了消除系统状态变量与其参考值之间的误差，定义滑模控制器的输入为系统变量及其参考值之差[18]。因此，根据滑模的存在性和可达性条件，以及系统正常运行的动态品质要求[3-5]，本文基于有功功率误差和网侧无功功率误差设计功率内环的滑模面:

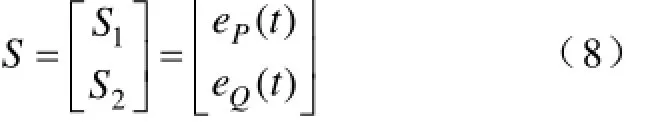
式子（8）中eP(t)=Pref-P 为网侧内环有功功率的差值，eQ(t)=Qref-Q 为网侧内环无功率的差值。

3.1.2 滑模控制器的设计

本文采用指数趋近率设计滑模控制器[4]，用于减弱滑模变结构控制的抖振，其形式如下

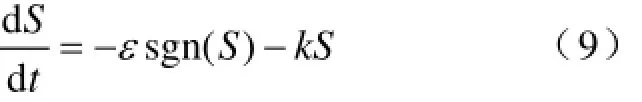
通过合理选择参数ε(ε＞0)、k(k＞0)，既可以保证滑动模态的动态品质，又可以减弱控制信号的高频抖振，式（9）让系统状态量以变速和指数两种速率趋向滑模面，提高趋近速率，当接近滑模面时，指数趋近律的速度接近为零，有效减小进入滑模面时的抖动，为有效减小系统抖动，可用连续函数（10）替代滑模控制器中的开关函数[19]。

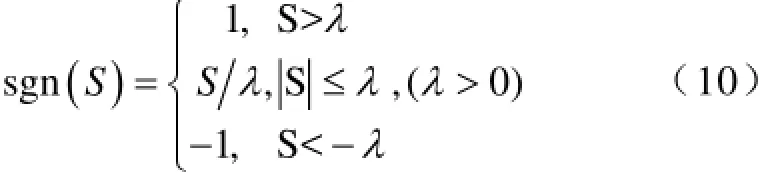
对滑模面求导，即对式子（8）求导得:

将系统记作:

令滑模面的导数式（11）等于零，由于有功功率给定Pref来自直流侧，无功功率给定Qref为零，采用如式（9）的指数趋近率，将式（5）代入式（11）中，按照式子（12）形式求解，得:

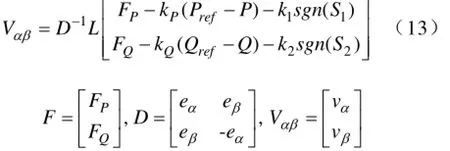
其中sgn为饱和函数，控制参数都为正数，选择较大的kP、kQ可以保证系统快速性，在保证系统鲁棒性的前提下，选择较小的k1、k2可以减少系统的抖振。

3.1.3 滑模控制律的稳定性

选取李亚普诺夫函数:2T VSS=，对时间求导得:

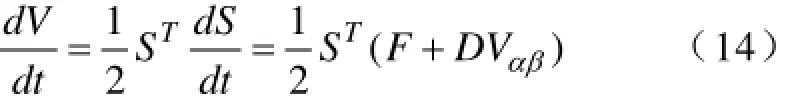
滑模面的导数采用如式（9）所示的指数趋近律形式:

式中，kP、kQ、k1、k2分别为设定的指数趋近律正参数，将式（15）代入式（14）中，得:

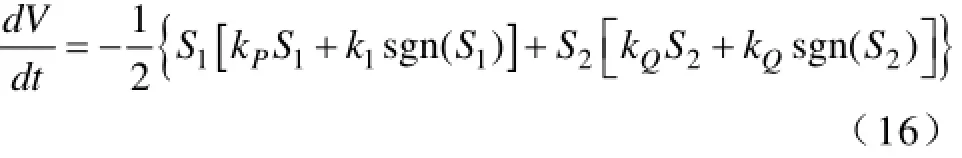
由于S1(2)与kP(Q)S1(2)+k1(2)sgn(S1(2))符号相同,表明:滑动面函数S1(2)与滑动面函数的变化趋势dS1(2)dt符号相反，当系统状态变量离开滑动面以后，最终可以回到滑动面，因此式子（16）:dVdt＜0成立，即可确保滑动模态的存在性和可达性。

3.2电压外环滑模控制器的设计

3.2.1 分析电压外环的非线性

根据整流器在静止α-β坐标系下的数学模型，由式子（4）可知，经过同步旋转变换后，直流母线电压vdc与电流id和电流iq均相关，采用线性PI调节器利用d轴电流id对直流母线电压进行跟踪，难以得到较好的控制性能，构造以电压平方为控制量间接实现电压闭环的滑模控制策略，以提高系统的动态特性和稳态精度。

3.2.2 滑模控制器的设计

整流器工作在单位因数状态下，无功功率为零，则Qref=Q=0；电压外环通过直流电压来描述瞬时有功功率的动态过程，根据式子（7）所描述的直流侧功率数学模型，结合文献[20]则选取滑模面为:

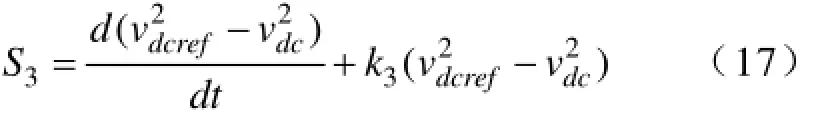
分析有功功率的滑模面，在任意一个开关周期内，不计电路中的损耗（电路等效阻抗损耗和开关损耗），且中点电位平衡，则式子（7）可变为:

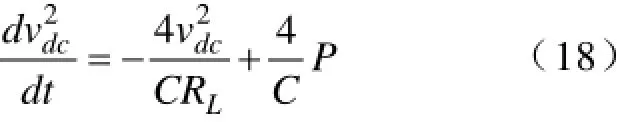
一个开关周期内，相对功率内环，直流电压的参考给定dcrefv默认为定值，则2dcref0 dv=；在滑模面上系统将会沿着0S=的轨迹产生滑动。将式（18）代入式（17）得:

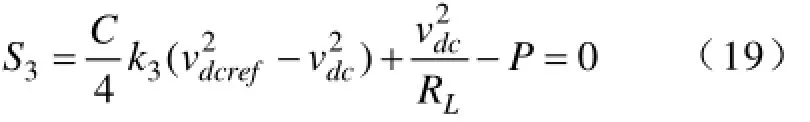
根据式（19），在一个开关周期内有功功率与给定值满足:Pref-P=0，则可得到: 3.2.3 滑模面的可达条件

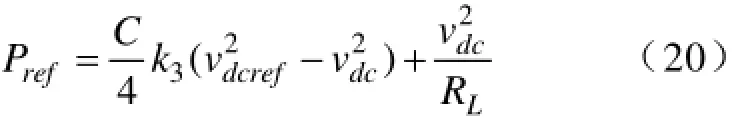
滑动模态存在是滑模变结构控制器应用的前提，虽然不同系统可到达性的条件形式不同，但其滑动模态存在的数学表达式为:

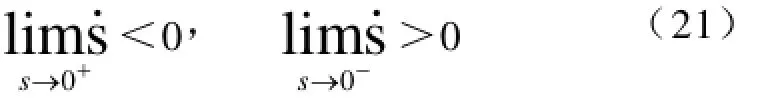
上式意味着在滑模切换面的邻域内，系统将于有限时间到达切换面，则可达条件的等价形式为:

通常将式（22）表达成李亚普诺夫函数的可达条件，定义()Vx为李亚普诺夫函数，则有:

对3S分析如下:

当3S＞0，Pref＞P时，需要在有限时刻内增大P以满足3ddSt＜0；当3S＜0，Pref＜P时，需要在有限时刻内减小P以满足3ddSt＞0；实际值要时刻跟随给定值，同时内环带宽大于外环带宽以符合系统稳定性要求。

3.3Vienna整流器的双闭环滑模控制器系统

由上述分析，可以得到基于滑模控制的三相Vienna整流器双闭环控制原理框图，如图2所示。根据检测到的三相电源电压和电流，利用在静止坐标系下的公式（3），估算求得瞬时有功和无功功率，外环控制的输出作为内环有功功率的给定值，无功给定设定为零（Qref=0），功率误差利用式（13）求得vα与vβ进行空间矢量调制。

从图2可知，功率内环无需同步速旋转坐标变换和电网电压的相位信息,控制结构简单；电压外环将vdc的数值平方作为反馈量，其效果等效于增加直流增益，且不影响系统稳定性，经过放大的误差使电压vdc快速跟随其给定值，加快系统的响应速度。

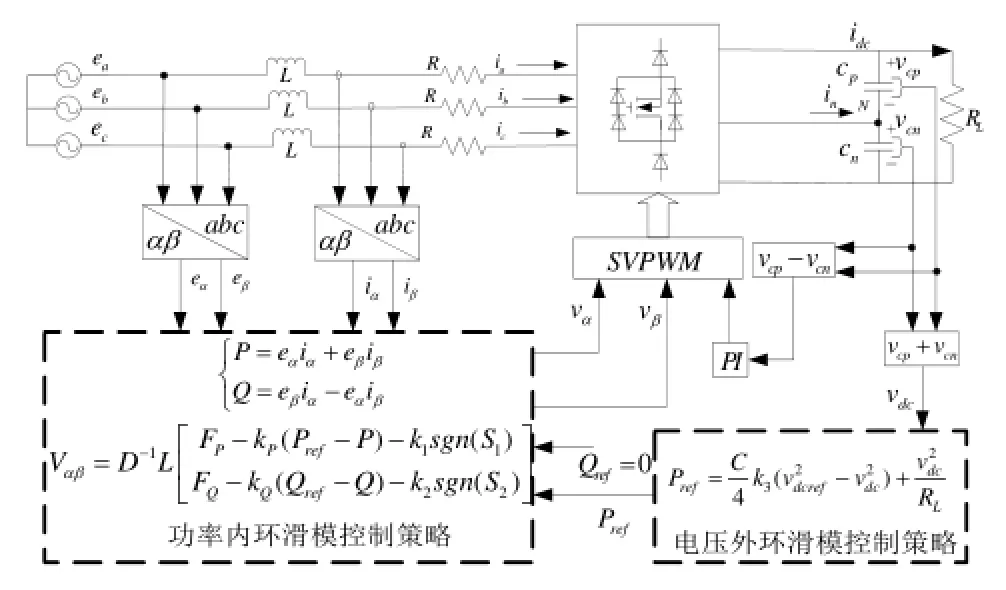
图2 三相Vienna整流器控制框图Fig.2 The control block diagram of three-phase Vienna rectifier

4 仿真与实验

4.1仿真系统

为验证所提控制策略的有效性，建立基于MATLAB/Simulink的仿真模型，调制策略利用加入中点电位平衡因子的SVPWM调制算法，为搭建实验样机提供仿真参考，同时将新型双闭环滑模控制与传统双闭环PI控制策略进行比较。其系统仿真参数如下:三相电压的有效值为110V/50Hz；输出直流电压为300V；三相输入电感为2mH；直流侧两个电容为2 200μF；额定输出功率为2kW，开关频率15kHz。仿真实验中，传统双闭环PI控制器根据本身特性，按照二阶模型并综合考虑系统动态性能和稳态性能进行设计，内环控制参数为kp=50，ki=10，外环控制参数为kp=0.5，ki=30；在双闭环滑模控制策略中功率内环的控制参数kp=5 500，kQ=3 500，k1=4 000，k2=4 000，λ1=200，λ2=150，外环滑模控制器的仿真控制参数k3=120。

图3和图4分别为2种控制方法的系统启动和负载突变时电压、功率响应波形图。在系统启动时，从图3中可以看出，采用传统双闭环PI控制方法时，电压超调严重，超调电压接近350V（参考电压300V），直流输出电压到达稳定值所需要时间长，大约需要0.016s，输出功率到达稳定状态的时间与直流电压到达稳定时间相同，另外中点电位平衡所要的时间长。而采用双闭环滑模控制方法时，仿真结果如图4所示，电压到达稳定值所需要时间约0.005s，稳定前的超调量大约为5V从不控到可控直流侧电压超调小，输出功率能够快速到达稳定状态，并且超调小，中点电位平衡能够快速实现；这验证了采用外环滑模控制方法可以快速强迫系统运行轨线快速向滑动流形移动，提高系统的响应速度和加速系统的收敛过程，从而使系统快速到达稳定状态。

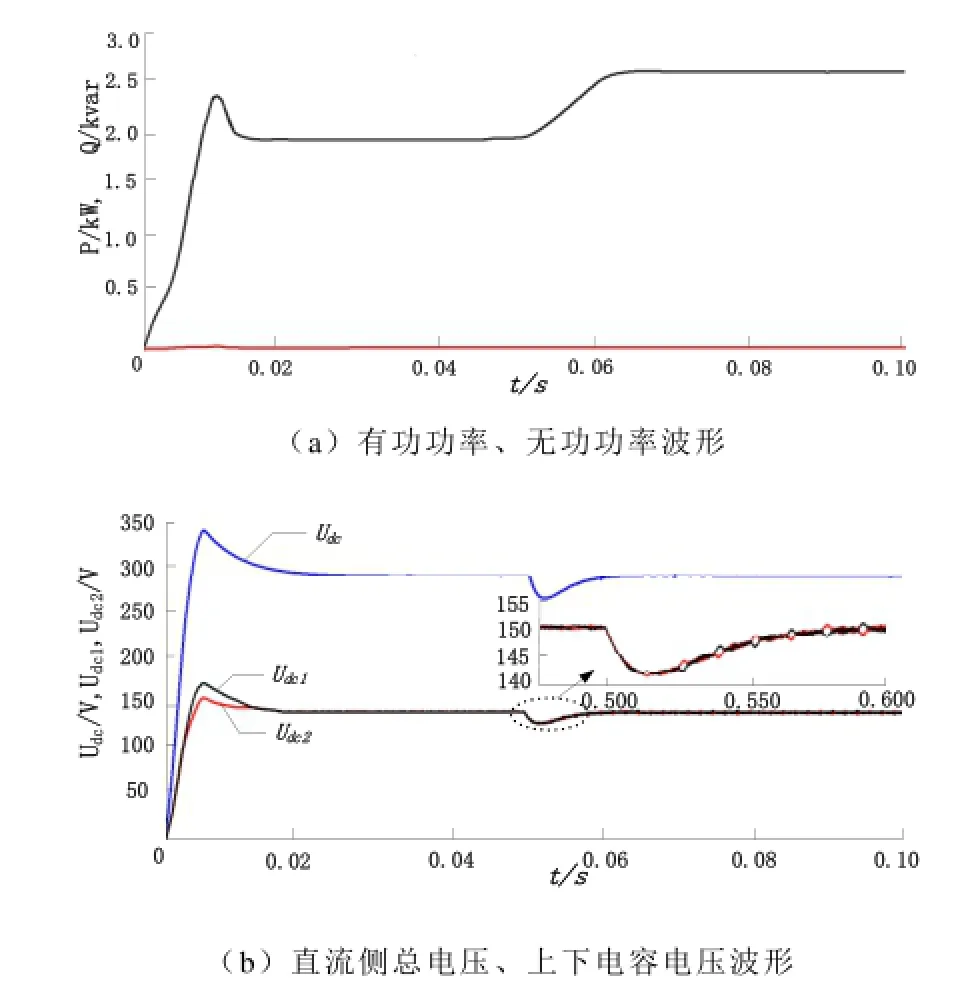
图3 传统双闭环PI控制方法下系统启动及负载突变时电压、功率仿真波形Fig.3 Voltage waveforms, power waveforms during system startup and load step change with dual closed-loop PI control method

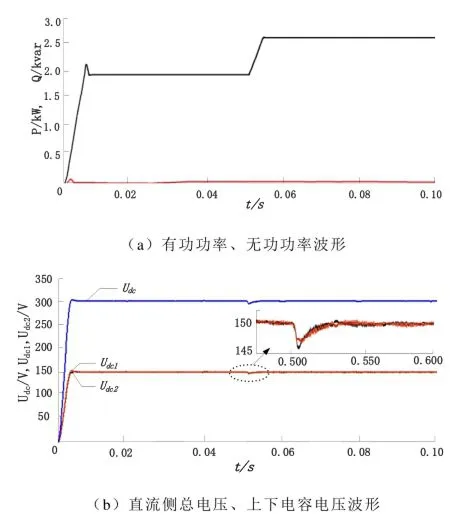
图4 新型双闭环滑模控制方法下系统启动及负载突变时输电压、功率仿真波形Fig.4 Voltage waveforms, power waveforms during system startup and load step change with a novel dual closed-loop slide mode control

在0.05s时，系统发生负载突变，从额定功率2kW升至2.6kW，从放大图中可以看出，采用双闭环滑模控制方法电压波动小，大约为5V，直流电压能够快速的恢复到参考给定值，优势十分明显，从功率图4a可以看出:功率内环滑模控制与外环电压滑模控制相结合能够快速的跟踪功率变化，到达稳定功率式时的功率超调量小，系统工作在单位功率因数状态下，在功率突变时，系统被迫重新快速回到滑模面上。上述结果表明:在系统稳定运行后，系统运行轨迹就被限制在内环功率滑模面上移动，即运动轨迹方程S=0，说明了功率内环滑模控制方法的鲁棒性能好，并验证了功率内环滑模控制具有快速精确调节功率的性能。

图5a和5b分别为2种控制方法下Vienna整流器输出电压、电流波形，列出启动时和负载突变时（0.01s，2kW→2.6kW）B相的电压、电流波形进行比较分析。两图中电压与电流在稳定运行时能保持同相位，说明两种控制方法都能确保整流器工作在单位功率因素状态下。而采用双闭环滑模控制后装置在启动时、负载突变时稳定时间有所缩短，大约0.004s便可重新达到稳定，同时电流在负载变动时电流畸变率小，如图5b所示，这说明双闭环滑模控制具有良好的响应速度和精确性。

图5 B相电压、电流波形和相位关系Fig.5 Voltage and current waveforms of B phase, phase relationship

为进一步分析负载变动时对电流控制的精确性，图6对本文所述方法中B相电流进行频谱分析，分别分析负载突变时和稳定运行时的B相电流谐波含量，结果如图6a和6b所示，负载突变时谐波含量为3.37%，加载稳定运行后谐波分量明显减少，电流THD将至1.84%，从而降低输入电流波形畸变率，保证输入电流质量。

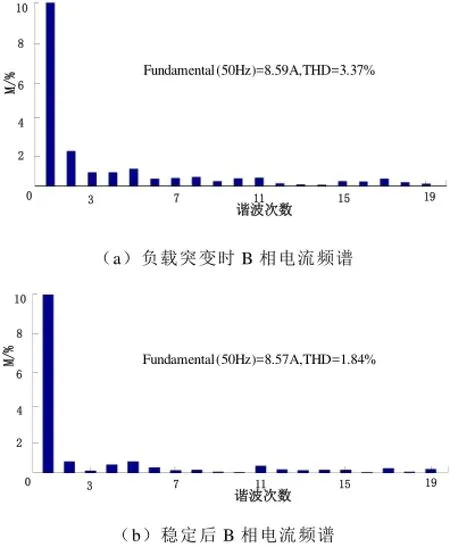
图6 电流频谱Fig.6 Current spectrum

4.2实验系统

按照图1的拓扑结构搭建实验样机，用来验证所提方法的有效性，电路基本参数与仿真相同，实验装置如图7所示，其控制器采用TMS320F2812DSP芯片作为核心运算、采样控制以及驱动信号的分配等。双向开关由1个IRF460MOS功率管和1个GBJ25120整流桥组成，快恢复二极管采用IXYS公司的DSEI12-06A。

图7 实验样机Fig.7 Experimental system

实验记录采用电能质量分析仪E6000和示波器泰克TBS1000，图8记录了两种控制方法下的总直流电压、有功功率、无功功率和B相电流对比波形图；图9记录两种控制法下装置稳定运行时三相电流的谐波含量对比图。

如图8所示，2种控制方法均能达到控制要求，但采用双闭环滑模控制控制方法时，电压、功率超调小，到达稳定时间短；负载突变时电流畸变小且到达稳定时间短；这与仿真系统结论一致。

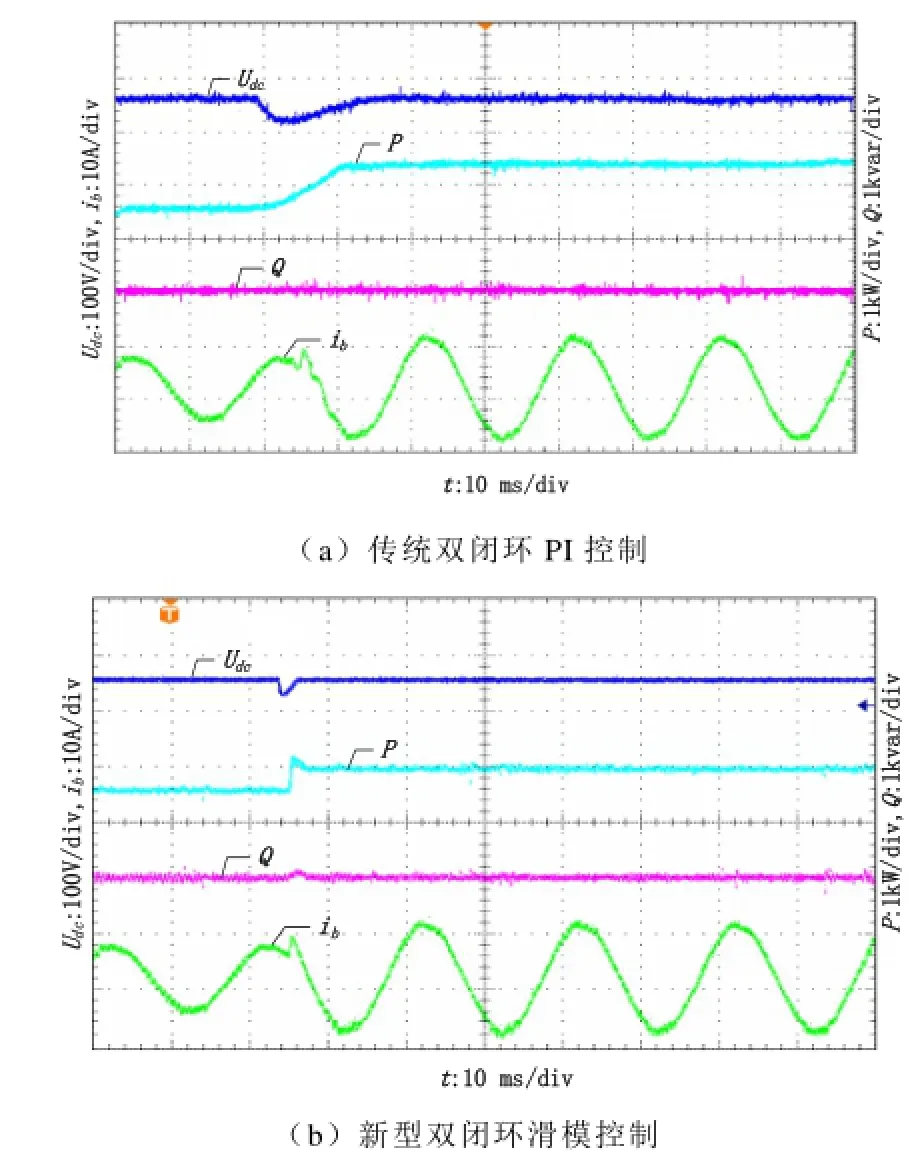
图8 电压、电流以及功率波形图Fig.8 Voltage waveforms, current waveforms and power waveforms

图9 b为双闭环滑模控制方法下整流器工作在额定状态下三相电流谐波的含量图，稳定运行时，三相电流平均谐波含量为2.04%，并未达到仿真中1.84%的效果，且负载突变时电流轻微畸变，这是由于实际运行中功率器件运行和电网存在少量谐波，与传统双闭环PI方法相比谐波量明显降低，图9a所示，三相电流平均谐波含量约为4.11%；另外在负载变动时，通过图8所示中电流畸变形状可以得出双闭环滑模控制方法具有较好的动态性能和抗干扰性能。

图9 三相电流谐波含量Fig.9 THD of three phase currents

5 结论

本文针对三相Vienna整流器设计一种新型双闭环滑模控制策略，建立该整流器的滑模变结构控制模型，与传统双闭环PI控制算法相比，该算法的控制结构简单，运算量小，引入电压平方反馈使系统具有良好的动态电压跟踪效果。利用仿真与实验进行对比分析，结果表明:在系统启动和负载突变时，采用双闭环滑模控制既改善了系统响应速度，又提高了系统的抗干扰性能；同时双闭环滑模控制算法能满足系统的控制性能要求:网侧为单位功率因数，输入电流正弦度高且谐波含量低，输出直流电压稳定且纹波小等。因此，本文所述的双闭环滑模控制策略具有良好的应用价值。

[1] 刘晓, 张庆范, 侯典立. 矩阵式整流器的滑模变结构控制[J]. 电工技术学报, 2013, 28(4): 149-156, 164.

Liu Xiao, Zhang Qinfan, Hou Dianli. Sliding mode variable structure control of matrix rectifiers[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 149-156, 164.

[2] 郑宏伟, 饶益花, 陈文光. 三相电压型PWM整流器的双滑模控制方案研究[J]. 电源学报, 2014, (01): 96-102.

Zheng Hongwei, Rao Yihua, Chean Wenguang. Double sliding mode control for three-phase voltage source PWM rectifier[J]. Journal of Power Supply, 2014, (01): 96-102.

[3] 侯世英, 宋星, 孙韬, 等. 基于滑模控制的新型三相双频并网逆变器[J]. 电力自动化设备, 2011, 31(12): 39-43.

Hou Shiying, Song Xing, Sun Tao, et al. Three phase double frequency grid-connected inverter based on sliding mode control[J]. Electric Power Automation Equipment, 2011, 31(12): 39-43.

[4] J. Hu, H. Nian, B. Hu, Y. He, and Z. Q. Zhu, "Direct active and reactive power regulation of DFIG using sliding-mode control approach, " IEEE Transactions on Energy Conversion, vol. 25, pp. 1028-1039, 2010.

[5] 唐勇奇, 赵葵银, 汪超. 基于滑模变结构控制的三相PWM整流器[J]. 电力自动化设备, 2006, 26(5): 39-41.

Tang Yongqi, Zhao Kuiyin, Wang Chao. Three-phase PWM rectifier based on sliding-mode variable structure control[J]. Electric Power Automation Equipment, 2006, 26(5): 39-41.

[6] Fernando S J. Sliding-mode control of boost-type unity power factor PWM rectifiers[J]. IEEE Transactions on Industrial Electronics, 1999, 46(3): 594-603.

[7] Youssef N B H, Fnaiech F, Al-Haddad K. Small signal modeling and control design of a three-phase AC/DC Vienna converter[C]. Industrial Electronics Society, 2003. IECON '03. The 29th Annual Conference of the IEEE, 2003: 656-661.

[8] Kanaan H, Al-Haddad K. Small-signal averaged model and simple control of a high-power-factor three-phase/ switch level fixed-frequency PWM rectifier for highpower telecommunications[C]. Telecommunications Energy Conference, 2004. INTELEC 2004. 26th Annual International, 2004: 449-456.

[9] Bel Haj Youssef N, Al-Haddad K, Kanaan H Y. Largesignal modeling and steady-state analysis of a 1.5kW three-phase/switch/level(vienna) rectifier with experimental validation[J]. Industrial Electronics, IEEE Transactions on, 2008, 55(3): 1213-1224.

[10] 宋卫章, 黄骏, 钟彦儒, 王丽娟. 带中点电位平衡控制的Vienna整流器滞环电流控制方法[J]. 电网技术, 2013, 37(07): 1909 -1915.

Song Weizhang, Huang Jun, Zhong Yanru, etal. A hysteresis current control method with neutral point potential balancing control for Vienna rectifier[J]. Power System Technology, 2013, 37(07): 1909 -1915.

[11] Lijun H, Bin L, Ming Z, et al. Equivalence of SVM and Carrier-Based PWM in Three-Phase/Wire/Level Vienna Rectifier and Capability of Unbalanced-Load Control[J]. Industrial Electronics, IEEE Transactionson, 2014, 61(1): 20-28.

[12] Rixin L, Fei W, Burgos R, et al. Average Modeling and Control Design for VIENNA-Type Rectifiers Considering the DC-Link Voltage Balance[J]. Power Electronics, IEEE Transactions on, 2009, 24(11): 2509-2522.

[13] Burgos R, Lai R, Pei Y, et al. Space Vector Modulator for Vienna-Type Rectifiers Based on the Equivalence Between Two- and Three-Level Converters: A Carrier-Based Implementation[J]. Ieee Transactions On Power Electronics, 2008, 23(4): 1888-1898.

[14] 何礼高, 陈鑫兵. 变电感参数三电平不可逆PWM整流器的电流PI优化控制[J]. 电工技术学报, 2011, 26(07): 203-209.

He Ligao, Chen Xinbing. Optimized PI current controller of three level unidirectional PWM rectifier under variable inductance[J]. Transactions of China Electrotechnical Society, 2011, 26(07): 203-209.

[15] 韦徵, 陈新, 陈杰, 等. 单周期期控制的三相PFC整流器输入电流相位滞后及闭环补偿[J]. 中国电机工程学报, 2013, 33(33): 42-49.

Wei Zheng, Chen Xin, Chen Jie, et al. Input current phase lag an closed loop compensation for threephase PFC rectifier based on one-cycle control strategy [J]. Proceeding of the CSEE, 2013, 33(33): 42-49.

[16] 王智, 方炜, 刘晓东. 数字控制的单周期PFC整流器的设计与分析[J]. 中国电机工程学报, 2014, 34(21): 3423-3431.

Wang Zhi, Fang Wei, Liu Xiaodong. Design and analysis of digitally controlled high power factor rectifiers based on one-cycle control[J]. Proceeding of the CSEE, 2014, 34(21): 3423-3431.

[17] 尚磊, 孙丹, 胡家兵, 等. 三相电压型并网逆变器滑模变结构直接功率控[J]. 电力自动化设备, 2010, 34(14): 79-83.

Shang Lei, Sun Dan, Hu Jiabing, et al. Sliding mode variable structure based direct power control of three-phase grid-connected voltage source inverters[J]. Electric Power Automation Equipment, 2010, 34(14): 79-83.

[18] 李生民, 何欢欢, 张玉坤, 等. 基于滑模变结构的双馈风力发电机直接功率控制策略研究[J]. 电网技术, 2013, 37(07): 2006-2011.

Li Shengming, He Huanhuan, Zhang Yunkun, et al. A sliding mode variable structure-based direct power control strategy for doubly fed induction generator[J]. Power System Technology, 2013, 37(07): 2006-2011.

[19] Shang L, Hu J. Sliding-mode-based direct power control of grid-connected wind-turbine-driven doubly fed induction generators under unbalanced grid voltage conditions. IEEE Transactions on Energy Conversion, 2012, 27(2): 362-373.

[20] Huang Jingjing, Zhang Aiming, et al. Improved direct power control for rectifier based on fuzzy sliding mode[J]. Control Systems Technology, IEEE Transactions on, 2014, 22(3): 1174-1180.

A Novel Dual closed-Loop Control Strategy based on Sliding-Mode Variable Structure of Vienna-type Rectifier

Ma Hui Xie Yunxiang
（School of Electrical Power South China University of Technology Guangzhou 510641 Guangdong Province China）

For the constant and sensitive coefficient of conventional dual closed-loop PI controllers, the Vienna-type rectifier have some shortcomings under startup situation and load sudden change within a large permitted disturbance, namely slow dynamic response, poor anti-disturbance ability and large input current harmonics(THD).Since a novel dual closed-loop nonlinear control strategy was proposed in this paper, which adopted direct power control based on sliding mode control (SMC-DPC)for inner loop without transforming to d-p rotating coordinate system and used sliding mode control with the square of voltage as the feedback for the outer loop; The new control system diagram was derivate in detail and the realized method was shown in this paper. Both the simulation and experimental results are utilized to analyze and compare the performances of the novel dual closed-loop control algorithm based on sliding-mode control and conventional PI control scheme, which show that the proposed scheme is much better, exhibits fast dynamic response and possesses good robustness to startup and load step change.

Vienna-type rectifier, sliding-mode variable structure, dual closed-loop control, direct power control, square of the voltage

TM46

2014-09-10

马 辉 男，1985生，博士研究生，主要从事电力电子功率变换方面的研究。

谢运祥 男，1965生，博士，教授，主要研究方向为电力电子功率变换及微机控制技术。