螺旋磁场作用下磁致伸缩位移传感器的输出电压模型及实验

张露予 王博文 翁 玲 孙 英 王 鹏

螺旋磁场作用下磁致伸缩位移传感器的输出电压模型及实验

张露予 王博文 翁 玲 孙 英 王 鹏

（河北工业大学电磁场与电器可靠性省部共建重点实验室 天津 300130）

基于魏德曼效应和压磁效应建立了螺旋磁场作用下磁致伸缩位移传感器的输出电压模型，计算了磁致伸缩位移传感器的输出电压。计算结果表明输出电压与螺旋磁场间存在线性关系。当激励磁场与偏置磁场均为3kA/m、螺旋磁场强度为4.24kA/m时，输出电压的计算值达到18.09mV，计算结果与实验结果的变化趋势一致，数值基本吻合，表明了建立的输出电压模型的正确性。基于建立的模型，可以确定传感器激励磁场与偏置磁场的范围，研究可为磁致伸缩位移传感器的优化设计提供理论基础与指导。

输出电压模型 螺旋磁场 魏德曼效应 磁致伸缩

1 引言

磁致伸缩位移传感器在精密位移控制和界面测量[1-2]等领域有广泛的应用，研究者在磁致伸缩位移传感器的数学模型及实验方面做了诸多研究工作。文献[3-4]分析了磁致伸缩位移传感器的工作原理，确定了输出电压与激励磁场之间存在正相关关系。文献[5-7]研究了磁致伸缩位移传感器的输出特性，给出了传感器输出电压的计算式，但计算式过于复杂，难于应用所建立的模型进行数值计算。然而，到目前为止，在螺旋磁场作用下磁致伸缩位移传感器的影响因素仍不清楚，尚未建立传感器的输出电压计算模型。本文基于魏德曼效应和压磁效应从理论上研究了磁致伸缩位移传感器输出电压与螺旋磁场间的关系，建立了磁致伸缩位移传感器的输出电压模型，并对铁镍磁致伸缩位移传感器进行了实验。通过输出电压的计算与实验的对比分析，表明了所建立模型的正确性，确定了激励磁场、偏置磁场对传感器输出电压的影响规律，提出了设计传感器时磁场应满足的条件，研究对磁致伸缩位移传感器的磁场优化设计具有重要的指导意义[8-10]。

2 螺旋磁场下磁致伸缩位移传感器的输出电压模型

2.1传感器输出电压模型

磁致伸缩位移传感器的输出电压模型旨在建立输出电压与螺旋磁场的关系，并研究激励磁场、偏置磁场与材料特性等参数对传感器输出电压的影响规律。

根据法拉第电磁感应定律，感应电动势e可表示为

式中，N为探测线圈匝数；S为单匝线圈面积；φ为磁通量；B为磁感应强度；t为时间。

波导丝是位移传感器的核心元件，螺旋磁场H(r)是由激励磁场Hi(r)和偏置磁场Hm耦合产生的。激励磁场由激励脉冲电流产生，是关于波导丝半径r的位置函数，沿波导丝径向分布；轴向偏置磁场可由永磁体提供。螺旋磁场的方向由偏置磁场与螺旋磁场间的夹角决定，用公式可以表示为

磁致伸缩位移传感器信号的产生源于磁致伸缩材料的魏德曼效应。在魏德曼效应作用下，磁体中的磁畴被轴向偏置磁场磁化，当受到周向激励磁场的作用时，磁畴发生局部偏转，质点在强动载荷的作用下偏离其平衡位置运动，由于质点间的相互作用，质点的振动由近及远的传播形成了应力波。当应力波到达探测线圈时，在磁致伸缩逆效应的作用下，机械应力的改变导致波导丝中磁感应强度发生变化，因此在探测线圈两端便产生感应电压。传播过程中机械能与磁场能[11]间的转换可表示为

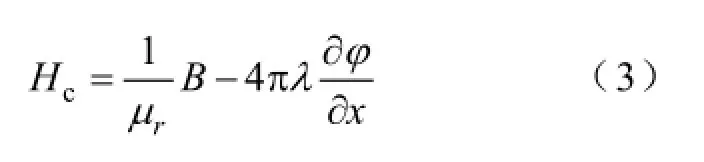
式中，Hc是在磁致伸缩逆效应的作用下由波导丝中磁感应强度和机械应力的变化而产生的磁场；μr为相对磁导率；xφ∂∂为角应变；λ为角应变引起的磁场变化率，它应与磁致伸缩效应等相关，可通过实验确定。

探测线圈开路时，不能形成闭合回路，磁场强度Hc为零，影响磁感应强度的主要因素是机械应力，式（3）可以表示为

为分析波导丝中的机械应力，将磁致伸缩波导丝划分成许多的小单元，这些小单元可等效成磁畴的结构，如图1所示。

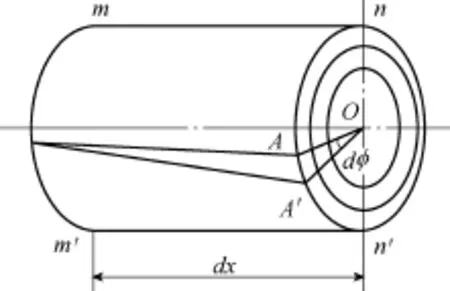
图1 波导丝中小单元的扭转变形Fig.1 Torsional deformation of the waveguide wire

在螺旋磁场作用下波导丝中的磁畴发生扭转变形，截面n-n' 相对于截面m-m' 刚性转动了φd角度，半径OA转到OA'的位置，根据圆轴扭转的平面假定[12]，波导丝的角应变可用波导丝所受的扭矩T来描述。

式中，G为材料的剪切模量，G=E/2(1+ν)；E为杨氏模量；ν为泊松比；Ia为截面的极惯性矩。

扭矩的大小能直观的反应出材料受螺旋磁场作用后的变形程度，波导丝上的扭矩[13]为式中，φm、L和Ln分别为轴向磁通量、波导丝长度和探测线圈长度。

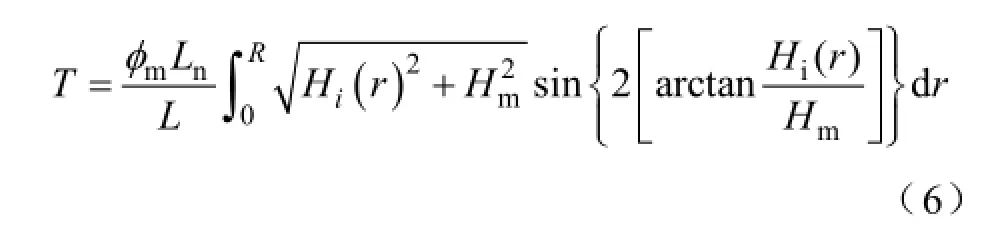
式（6）积分项中含有反正切函数、正弦函数和激励磁场的位置函数，计算比较复杂。考虑到波导丝上的脉冲电流频率较高，电流分布存在趋肤效应，波导丝表面处的电流很大，激励磁场值最大，此处的魏德曼效应显著，为了简化计算，可以用波导丝表面处的激励磁场Hi(R)来代替式（6）中的激励磁场Hi(r)，式（6）可简化为

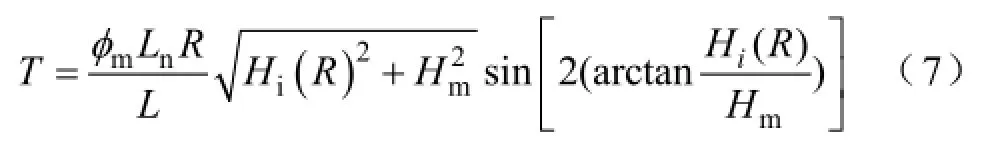
在磁致伸缩逆效应的作用下，波导丝中机械应力[14]的改变导致磁感应强度发生变化，将线圈中的磁感应强度对时间微分可得磁致伸缩位移传感器的输出电压，应力波通过探测线圈所用的时间为t，应力波波速为0ν=，将式（4）、式（5）和式（7）代入式（1）可得

式（8）为螺旋磁场作用下磁致伸缩位移传感器的输出电压方程，根据电压信号传递的时间可以确定测试的位置。表明磁致伸缩位移传感器的输出电压由磁致伸缩波导丝的角应变引起的磁场变化率、相对磁导率、波导丝半径、长度、杨氏模量、泊松比、密度、极惯性矩、探测线圈匝数、横截面积、磁通量轴向分量、偏置磁场和激励磁场等参数决定。可见，影响磁致伸缩位移传感器输出电压的因素诸多，比较复杂。当确定了波导丝的材料、探测线圈的结构，感应电压的大小主要取决于螺旋磁场的特性。

2.2传感器输出电压的数值计算

应用式（8）对螺旋磁场作用下传感器的输出电压进行了数值计算，计算中采用的参数[15]及由实验确定的角应变引起的磁场变化率λ，见表。

表 计算参数及由实验确定的λ值Tab. The calculating model parameters

当偏置磁场强度为3kA/m时，利用式（8）计算得到的传感器激励磁场与输出电压的关系如图2所示。

图2 激励磁场与传感器输出电压的关系曲线Fig.2 Output voltage VS excitation magnetic field

从图2可知，当波导丝处于较低的激励磁场时，魏德曼效应不够显著，输出电压值较小。随着激励磁场增加，材料内部的磁畴在强动载荷作用下偏离其平衡位置运动，激发出应力波，出现明显的魏德曼效应，输出电压随激励磁场的增加而线性增加。当激励磁场等于3kA/m，即激励磁场与偏置磁场相等时，输出电压达到线性段的顶端。这是因为输出电压不仅与激励磁场有关，还与偏置磁场相关。当激励磁场与偏置磁场相等时，螺旋磁场的方向为45°，式（8）中与角度相关的计算项取得最大值，导致传感器输出电压达到线性段的顶端；当激励磁场强度大于3kA/m后，波导丝中机械应力导致的磁化强度变化减小，输出电压随激励磁场增加而缓慢增加。

当激励磁场为2.5kA/m时，偏置磁场与传感器的输出电压关系如图3所示；当偏置磁场小于2.5kA/m时，传感器的输出电压随偏置磁场的增加而快速增大。基于磁畴理论，偏置磁场使波导丝中的磁畴发生畴壁位移或磁畴转动，磁化强度急剧增大，导致传感器输出电压快速增大。当偏置磁场大于2.5kA/m时，磁化强度趋于饱和，表现为输出电压缓慢增加。

图3 偏置磁场与传感器输出电压的关系曲线Fig.3 Output voltage VS bias magnetic field

图2 和图3的结果表明传感器的输出电压值都是在激励磁场与偏置磁场数值相等时出现转折点，并达到线性段的顶端。考虑当激励磁场与偏置磁场相等时，应用式（2）、式（8）计算螺旋磁场与传感器输出电压的关系，计算结果如图4所示。

图4 螺旋磁场与传感器输出电压的关系曲线Fig.4 Output voltage VS helical magnetic field

图4 表明螺旋磁场与输出电压之间存在线性关系。当激励磁场与偏置磁场强度均为3kA/m，螺旋磁场强度为4.24kA/m时，传感器输出电压的计算值为18.09mV。因此设计磁致伸缩位移传感器时，应满足:①激励磁场与偏置磁场相等或接近；②较大的螺旋磁场。综合考虑输出电压信号强度，可将偏置磁场与激励磁场设定在2～3kA/m范围内。

3 实验结果与分析

3.1实验测试系统的组成

搭建实验测试系统[16]如图5所示。将直径0.5mm、长度1m的磁致伸缩波导丝固定在内径6mm，外径8mm的铁氟龙塑料管内（使波导丝保持垂直，无任何弯折），底端穿过橡胶棒紧固（以减少有效信号被塑料管壁吸收），再套入内径9mm、外径14mm、壁厚2.5mm的316L不锈钢探杆内。实验中使用的电源为稳压电源和可调电源，稳压电源为后续的信号调理电路提供稳定的工作电压，可调电源用于控制激励脉冲的电压幅值，电压调节范围为0～32V。采用TFG6920A型信号发生器产生激励脉冲电流，脉冲频率设定1 800Hz，宽度为5μs，高电平15V。探测线圈穿过波导丝，固定在探杆的首端，用于信号的拾取，信号显示采用DPO3014型的四通道示波器，同时显示输入激励信号和输出感应电压信号。

图5 搭建实验测试系统Fig.5 The experiment testing system

3.2激励磁场对输出电压的影响

实验中脉冲激励电流的变化范围为0.5～7A，产生0.3～4.5kA/m范围的激励磁场。偏置磁场由永磁体提供，磁场强度为3kA/m，实验得到的激励磁场与输出电压之间的关系如图6所示。

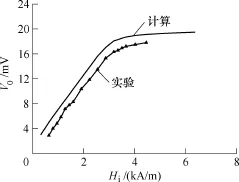
图6 激励磁场与传感器的输出电压关系Fig.6 The excitation magnetic field dependence of output voltage

从图6可知，激励磁场强度小于3kA/m时，较小的磁场增加会产生较大的输出电压增加；激励磁场强度大于3kA/m后，输出电压的变化趋势变缓；当激励磁场强度为2kA/m时，传感器的输出电压幅值可达10mV，能够明显的与干扰信号、杂波等区分，可有效拾取信号，提高系统的信噪比。因此，激励磁场应设定在2～3kA/m范围内。图6一并示出了计算结果，可见实验结果与计算结果的变化关系是一致的。

3.3偏置磁场对输出电压的影响

当激励磁场为2.5kA/m时，实验得到的偏置磁场与输出电压之间的关系如图7所示。偏置磁场由1.5kA/m增大到2.5kA/m时，传感器的输出电压幅值由6.39mV快速增长到12.15mV；继续增大偏置磁场，传感器的输出电压缓慢增加。从图6和图7的结果可见，输出电压随激励磁场、偏置磁场的变化趋势相同。当偏置磁场与激励磁场相等时，输出电压出现转折点，并达到较大值。

图7 偏置磁场与传感器的输出电压关系Fig.7 The bias magnetic field dependence of output voltage

3.4输出电压和螺旋磁场的关系

在研究传感器输出特性与螺旋磁场的关系时，可设激励磁场与偏置磁场相等。实验过程中同时改变激励磁场与偏置磁场的强度，并始终保持两者的强度相等，得到螺旋磁场强度与传感器输出电压的关系如图8所示。

图8 螺旋磁场与传感器的输出电压关系Fig.8 The helical magnetic field dependence of output voltage

图8 表明传感器的输出电压随螺旋磁场强度的增大而线性增加，实验结果与计算结果的变化趋势是一致的。

3.5误差分析

图6～图8中实验结果与计算结果的变化趋势是一致的。图6中当激励磁场为3kA/m时，实验值为16.32mV，计算值为18.09mV，实验值低于计算值，相对差值为10.84%。这主要是在应用式（8）计算输出电压时，采用波导丝表面处的激励磁场值Hi(R)来代替实际的激励磁场Hi(r)，即认为Hi(R)与半径r的位置无关。事实上Hi(r)=Ipr/(2πR2)，是关于波导丝半径r的位置函数，由于激励脉冲电流频率较高，电流分布存在明显的趋肤效应，导致波导丝表面处的激励磁场最大。为了简化计算，采用波导丝表面处的激励磁场值Hi(R)来代替实际的激励磁场Hi(r)，结果导致计算值高于实验值；另一方面，应用式（8）进行数值计算时，假设材料的磁致伸缩效应、磁导率为常数，忽略了材料磁滞的影响，也可能导致计算值与实验值之间存在误差。

将激励磁场Hi(r)表示为波导丝半径r的线性函数，同时将杨氏模量表示为E=El(1-k2)，磁导率为μ=μσ(1-k2)，其中k为磁机械耦合系数[17]，与磁致伸缩效应密切相关。采用修正后的式（8）计算得到的螺旋磁场与输出电压之间的关系如图9所示，可见计算值与实验值误差明显减小，相对差值小于5%。

图9 修正后计算得到螺旋磁场与输出电压的关系Fig.9 Output voltage VS helical magnetic field after correction

4 结论

基于魏德曼效应、压磁效应建立了螺旋磁场作用下磁致伸缩位移传感器的输出电压模型，计算了磁致伸缩位移传感器的输出电压。计算表明螺旋磁场与输出电压之间存在线性增加关系。当激励磁场与偏置磁场强度均为3kA/m，螺旋磁场强度为4.24kA/m时，传感器输出电压的计算值为18.09mV。

实验结果与计算结果变化趋势相同，表明螺旋磁场作用下磁致伸缩位移传感器输出电压可以用模型描述。基于建立的模型，可以确定传感器激励磁场与偏置磁场的范围，同时确定了设计磁致伸缩位移传感器应满足的两个条件:①激励磁场与偏置磁场相等或接近；②较大的螺旋磁场。研究可为磁致伸缩位移传感器的优化设计提供理论依据与指导。

[1] Mohammad Reza Karafi, Yousef Hojjat, et al. A novel magnetostrictive torsional resonant transducer[J]. Sensors and Actuators A, 2013, 195： 71-78.

[2] 周翟和, 汪丽群, 沈超, 等. 基于CPLD的磁致伸缩高精度时间测量系统设计[J]. 仪器仪表学报, 2014, 35(1)： 103-108.

Zhou Zhaihe, Wang Liqun, Shen Chao, et al. Design of magnetostrictive high-precision time measurement system based on CPLD[J]. Chinese Journal of Scientific Instrument, 2014, 35(1)： 103-108.

[3] Hristoforou E, Hauser H, Ktena A. Modeling of magnetostriction in amorphous delay lines[J]. Journal of Applied Physics, 2003, 93(10)： 8633-8635.

[4] Hristoforou E, Dimitropoulos P D, Petrou J. A new position sensor based on the MDL technigue[J]. Sensors and Actuators A, 2006, 132： 112-121.

[5] Li Jiheng, Gao Xuexu, Zhu Jie, et al. Widemann effect of fe-ga based magnetostrictive wires[J]. Chinese Physics B, 2012, 21(8)： 087501-1-6.

[6] 代前国, 周新志. 大位移磁致伸缩传感器的弹性波建模与分析[J]. 传感技术学报, 2013, 26(2)： 195-199.

Dai Qianguo, Zhou Xinzhi. Modeling and analysis of elastic wave of large-range magnetostrictive displacement sensor[J]. Chinese Journal of Sensors and Actuators, 2013, 26(2)： 195-199.

[7] Deng Chao, Kang Yihua, Li Erlong, et al. A new model of the signal generation mechanism on magnetostrictive position sensor[J]. Measurement, 2014, 47：591-597.

[8] 杜治, 马蕊. 一种发电机励磁系统模型参数可辨识性分析方法[J]. 电力系统保护与控制, 2014, 42(22)：38-44.

Du Zhi, Ma Rui. Analysis method on parameter identifiability for excitation system model of generator [J]. Power System Protection and Control, 2014, 42(22)： 38-44.

[9] 高参, 汪金刚. 基于电场逆问题的高压输电线电压传感器技术与试验研究[J]. 电力系统保护与控制, 2014, 42(21)： 99-104.

Gao Can, Wang Jingang. Experiment and research of voltage sensor of high-voltage transmission line based on inverse problem of electric field[J]. Power System Protection and Control, 2014, 42(21)： 99-104.

[10] 高戈, 胡泽春. 含规模化储能系统的最优潮流模型与求解方法[J]. 电力系统保护与控制, 2014, V42(21)：9-16.

Gao Ge, Hu Zechun. Formulation and solution method of optimal power flow with large-scale energy storage [J]. Power System Protection and Control, 2014, V42(21)： 9-16.

[11] Roscoe C. Williams. Theory of magnetosrtictive delay lines for pulse and continuous transmission[R]. New Jersey： Bell Telephone Laboratories, 1954.

[12] 张耀, 王云霞, 曹小平. 工程力学（静力学+材料力学）[M]. 北京： 中国电力出版社, 2010： 69-105.

[13] Wang Yuemin, Zhu Longxiang. A theoretical computation model of magnetostrictive guided waves NDT output signals in ferromagnetic cylinder[J]. IEEE International Conference on Information Science Technology. 2012, March： 648-650.

[14] 王铮. 磁致伸缩直线位移传感器弹性波机理研究[D]. 太原： 太原理工大学, 2011.

Wang Zhen. Study of Elastic Waveform Mechanism of Magnetostrictive Line Position Sensor[D]. Taiyuan：Taiyuan University of Technology, 2011.

[15] 张露予, 李志鹏, 王博文, 等. 电磁式振动发电结构设计及谐振频率分析[J]. 河北工业大学学报, 2014, 43 (1)： 1-3.

Zhang Luyu, Li Zhipeng, Wang Bowen, et al. Design of electromagnetic vibration-powered generator and its resonant frequency analysis[J]. Journal of Hebei University Technology, 2014, 43 (1)： 1-3.

[16] 翁玲,罗柠,张露予,等. Fe-Ga合金磁特性测试装置的设计与实验[J]. 电工技术学报, 2015, 30 (2)： 237-241.

Weng Ling, Luo Ning, Zhang Luyu, et al. Design and experiment of a testing device for Fe-Ga magnetic properties[J]. Transactions of China Electrotechnical Society, 2015, 30(2)： 237-241.

[17] 王博文. 超磁致伸缩材料制备与器件设计[M]. 北京:冶金工业出版社, 2003:65-195.

The Output Voltage Model of Magnetostrictive Displacement Sensor in Helical Magnetic Fields and Its Experimental Study

Zhang Luyu Wang Bowen Weng Ling Sun Ying Wang Peng
（Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China）

The output voltage model of magnetostrictive displacement sensor has been founded based on the theory of Wiedemann effect and piezomagnetic effect. By this model, we can calculate the output voltage of sensor under helical magnetic field. It is found that there is a certain linear relationship between the output voltage and helical magnetic field. The calculating output voltage can be achieved to 18.09mV when the excitation magnetic field is equal to the bias magnetic field of 3kA/m and the helical magnetic field is 4.24kA/m. The accuracy and validity of the output voltage model has been validated with the consistence between the experimental data and calculating data. It helps to decide the optimal value of parameters including the excitation magnetic field and bias magnetic field intensity. This model provides a theoretical guidance for reasonable designing of the sensor structure.

Output voltage model, helical magnetic field, wiedemann effect, magnetostriction

TP212

张露予 女，1989年生，博士研究生，研究方向为磁性材料与器件。

国家自然科学基金（51171057，51201055），河北省引进留学人员资助项目（CG2013003001），河北省高等学校科学技术研究重点项目，（ZD2015085）和天津市高等学校科技发展基金（20140421）资助项目。

2014-12-24 改稿日期 2015-01-29

王博文 男，1956年生，教授，博士生导师，本文通讯作者，研究方向为磁性材料与器件。