基于多阶FDTD雷电感应过电压计算新方法

樊亚东 于建立, 詹清华 王建国 周 蜜 蔡 力 戚 为

（1.武汉大学电气工程学院 武汉 430072 2.东北电力大学输变电技术学院 吉林 132012 3.广东电网公司 佛山 528000 4.国网宁波鄞州供电局 宁波 315100 ）

1 引言

雷电是造成架空电力线路故障和事故最主要的外部因素[1]，长期以来线路防雷的工作重点集中在直击雷防护，对雷电感应过电压的研究相对较少[2]。随着配电线路雷击故障率在电网故障率中的比重越来越大，后者危害逐渐凸显。配电线路走廊密度大且绝缘水平低，对雷电感应过电压敏感程度高，其故障率占雷击总故障率的90%以上[2,3]。

传统的雷电感应过电压常用解析法计算：国内武汉高压研究院在上世纪 80年代分析拟合出峰值的近似计算式[4]；日本和西方一些国家的学者研究并提出相应计算公式，部分计算结果比观测值小很多[4]；Chowdhuri[5]于 1966年提出较为详细的解析计算式；Darveniza[5]于1971年提出考虑避雷线作用的近似计算公式。上述方法采用较多近似计算并不同程度忽略了部分影响因素（如大地电参数、回击电流波形等），计算精度无法保证。另外解析法计算对象多为线路感应电压峰值，无法得到波形，不能满足越来越复杂的防雷工作。数值方法既能更多的还原物理原型又能充分考虑各影响因素，是计算雷电感应过电压的有力工具。而雷电电磁脉冲（LEMP）的计算是数值方法中不可或缺的环节，关于 LEMP的理论计算除回击模型尚有不足外，传统的近似计算方法也存在一些凾待解决的问题，如：未考虑大地电导率[6]（将大地作为良导体）；局限于大地电导率较高情况[7]；局限于距回击通道较远（如大于100m）的场[8,9]；需要对近地面水平电场进行修正[10]等。Yee[11]提出的时域有限差分（FDTD）法在计算LEMP方面不仅能考虑大地电参数的影响，而且在粗糙、不均匀反射面的计算环境中有着独特的优势。

针对上述问题，本文采用数值方法模拟架空线雷电感应过电压，完善其从产生到发展的理论研究。重新推导了文献[12]计算架空线雷电感应过电压的Agrawal耦合模型，提出一种基于多阶 FDTD的数值计算方法。该方法采用一阶FDTD计算LEMP，采用二阶 FDTD[13]求解耦合电路方程，通过合理设置线路差分点实现两过程有效结合。所编软件适用于各种工况下架空线雷电感应过电压的计算。通过与火箭引雷试验实测数据比较，验证了本文方法的准确性。

2 物理模型

计算雷电回击通道周围的LEMP及其在架空线上激励产生的过电压，需要建立回击通道、大地和架空线路之间的整体化模型，如图1。在该模型中，将雷电回击通道作为Z坐标轴，X-Y平面表示为地面，地面落雷点为坐标系原点。对模型做如下设置：

图1 模型结构Fig.1 Scheme of model structure model

3 架空线雷电感应过电压计算方法

3.1 雷电回击通道电流

回击通道内雷电流的计算包括两个主要过程：1）、通道基电流i(0,t)的确定；2）、通道内回击模型的确定。目前业内应用最广泛的基电流函数有双指数函数[14]：

和 Heidler函数[15]：

国内外学者对雷电回击模型进行了大量的研究和讨论，本文采用了应用最多的工程模型[16]：

其中，I(z’,t)为任意高度z’和任意时间t的通道电流；u(t)是单位函数，t≥z’/vf时取 1 否则取 0；I(0,t)是通道基电流函数；p(z’)是电流衰减因子；v’是电流波传输速度；vf是回击速度。

3.2 多阶FDTD法计算雷电感应过电压

目前，解决外部电磁场激励下传输线感应电压的问题主要包括 Taylor法[17]、Agrawal法[18]和Rachidi法[19]等，三种模型所采用的激励场源不同。本文针对模型需求选择Agrawal法，提出基于多阶FDTD法计算线路感应电压。

该方法基本步骤如下：

1）选择回击模型并输入回击电流参数（基电流、通道高度和回击速度等）、架空线路参数（导线数、线径和空间距离等参数）以及时间步长和总时间长度等基础数据。

2）在计算空间内选取合适的单位长度划分空间网格，采用一阶FDTD法求解Maxwell方程计算回击通道周围空间的LEMP。

3）采用二阶FDTD法处理Agrawal耦合方程，得到图2所示电路模型的离散式，将步骤2）求得的空间水平电场和垂直电场代入电路方程的离散式中，迭代求解线路差分点的电压和电流。

图2 Agrawal 耦合模型电路图Fig.2 Circuit of Agrawal coupling model

4）输出每个时间步线路上“观测点”的电压和电流值，得到该点在LEMP激励下的时域响应。

3.2.1 FDTD法计算空间LEMP

雷电回击通道可视为轴对称的天线模型，产生的LEMP也具有轴对称性。因而三维场可简化为二维场，即含对称轴在内的半个剖面，模型如图1。轴对称情况下的电磁场具有TE模和 TM模两组独立的解，分别包括 Eφ、Hr、Hz分量和 Hφ、Er、Ez分量。天线辐射模型采用TM模，对应柱坐标系下的 Maxwell方程为[20]：

采用柱坐标Yee网格的方程差分格式为[20]：

式中，Er、Ez和Hφ分别表示LEMP中的水平电场、垂直电场和水平磁场。ε、σ和μ0分别为传播介质的电容率、电导率和磁导率。n、Δt、Δz和Δr分别为时间步、单位时间步长、垂直和水平方向空间网格步长。本文旨在实现有限区域内模拟无限空间的LEMP分布，须在计算区域边界设置吸收边界条件。工程上应用性能较好的吸收边界主要有Berenger提出的完全匹配层（PML）[20]、Chen提出的修正的完全匹配层（MPML）[20]以及Mur提出的单行波吸收条件[20]。本文对轴线和另外三个空间吸收边界分别采用安培环路定理和Mur吸收条件处理Maxwell方程，一阶FDTD法较为成熟不做重点介绍，故边界上具体离散格式不再赘述。

3.2.2 场线耦合方程的二阶FDTD离散方法

单导线 Agrawal模型等值电路耦合电路方程为[18]：

Vs为导线散射电压；ξg为大地阻抗的瞬态值，表示大地损耗的影响；符号⊗表示卷积积分；Ex(x,h,t)为差分点处沿导线方向水平电场值；L和C分别为导线单位长电感电容。对上式进行向量扩展，可得多导线模型的耦合矩阵方程[18]：

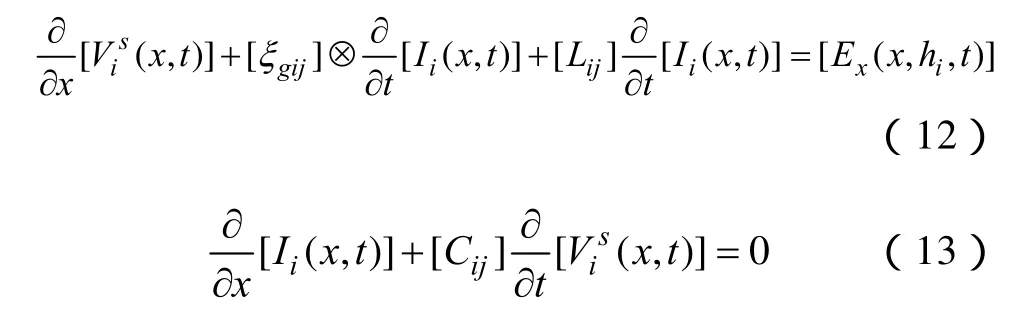
可见，耦合方程从单导线模型扩展到多导线模型将各变量扩展为变量矩阵。导线上总感应电压Vi(x,t)理解为散射电压和入射电压之和[18]：，其中入射电压，h为第 i根导线对地i高度，Ez(x,z,t)为差分点处垂直电场。为便于理解将模型简化处理，在两端设置边界条件如下：

R0和RL分别为线路始端和末端接地电阻。文献[12,13]采用一阶FDTD对式（10-11）离散处理，本文从提高数值稳定性和计算精度的角度对式（10-11）采用二阶FDTD法处理。分别在空间域x和时间域 t内作变形处理，式（10）和式（11）可改写为：

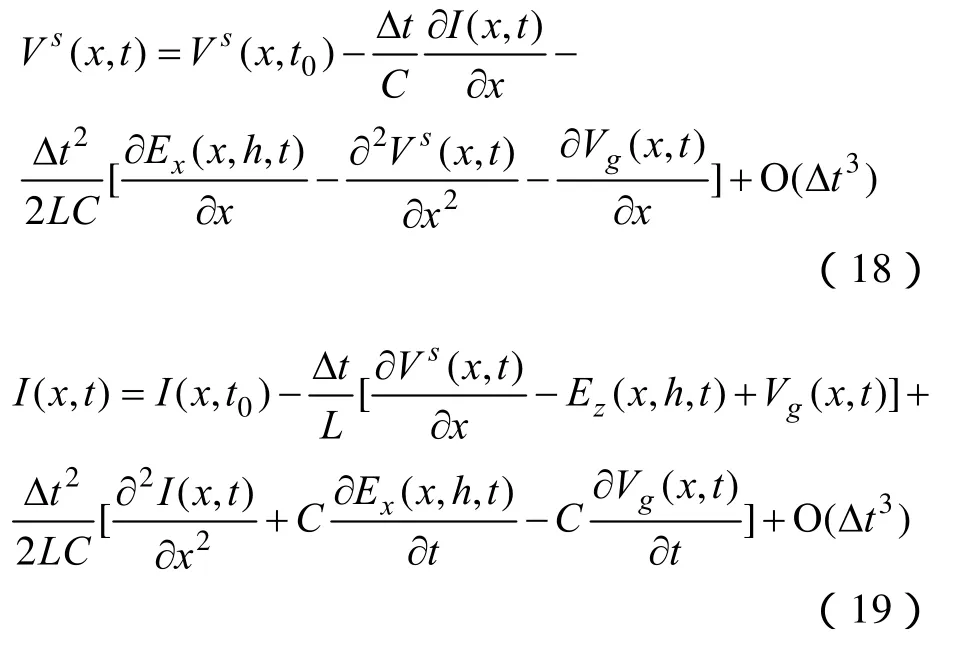
o(Δt3)为展开式余项。为方便使用FDTD处理方程，将待求变量和激励源变量写成空间步x和时间步t上更加直观的离散格式：

其中，Δx指线路差分点间单位长度，k表示沿线空间步数。将式（18-19）中散射电压、电流和水平电场对空间步长x和时间步长t的偏微分分别做一阶、二阶差分替换，即得式（18-19）的二阶FDTD离散形式:

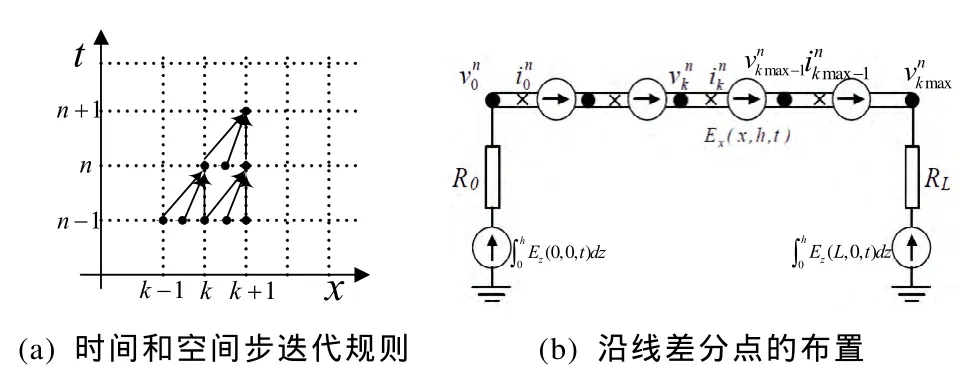
图3 一阶FDTD离散差分图Fig.3 Scheme of first order FDTD discrete difference

对于一阶 FDTD差分和二阶 FDTD差分的区别，可通过图3和图4得到清晰直观的理解：

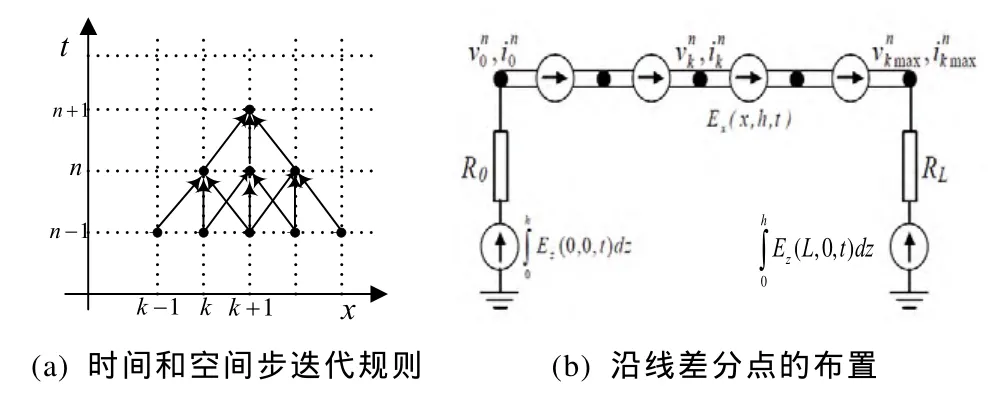
图4 二阶FDTD离散差分图Fig.4 Scheme of second order FDTD discrete difference

由图3可见一阶FDTD法电压计算与电流计算非同步进行，差分格式中散射电压节点和电流节点交替分布（理解为取节点电压和两节点之间电流为求解变量），若离散电压节点共有kmax个，则离散电流节点共有kmax-1个；图4的二阶FDTD差分格式中离散电压节点和电流节点重合为同一点，该离散格式的数值稳定性更高且能很好的简化线路不连续点（如避雷线接地点）的处理。按照上述过程对式（12-13）进行相同方法的推导和差分代换，得到考虑大地损耗的多导线模型二阶FDTD离散方程：

3.2.3 不连续点处理

线路中每级杆塔的接地位置和有装设避雷器的位置在计算中作为不连续点对待，该节点电压可采用图5模型单独计算：节点k的相邻两节点（k-2、k-1、k+1、k+2）在第 n+1时间步的散射电压和电流以及阻抗函数Γ和该处垂直电场 Ez为已知量。节点k的散射电压表达式为：其中，为接地点处分路阻抗中的电流，计算式为：；Γ为的函数表示该阻抗上的压降，分路阻抗若为线性电阻，则Γ =RgIg，可得：。对多导线情况可参照上文对单导线的扩展方法：

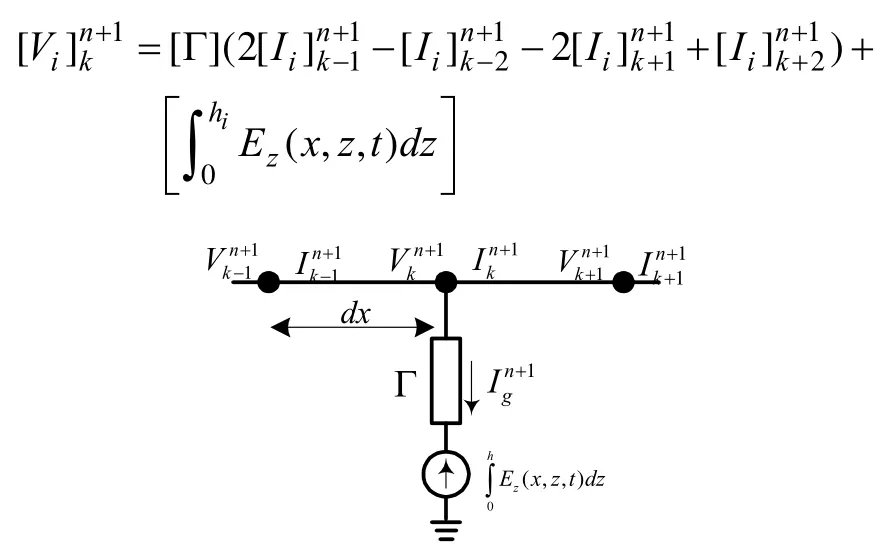
图5 线路不连续点模型图Fig.5 Scheme of discontinuity point model

若导线数为N，则矩阵[Γ]为：

4 计算方法验证

4.1 LEMP的计算与实测结果对比

LEMP的准确计算是研究线路雷电感应过电压的基础。为检验本文FDTD法计算LEMP，对以下火箭引雷试验进行计算对比。

佛罗里达州国际雷电研究测试中心（ICLRT）在2000年7月11日人工引雷方法测得Flash S0022,stroke 1[21]。实测15m处地面垂直电场如图6a。按照实测雷电流波形采用一个 Heidler函数与一个双指数函数叠加拟合基电流，FDTD法计算电场如图6b。

图6 实测电场与计算电场对比Fig.6 The measured electric field and calculation

由以上算例可见，本文FDTD法计算电场结果与实测电场基本吻合，证明LEMP算法正确性。

4.2 雷电感应过电压的计算与实测结果对比

1 数值计算与火箭引雷试验对比

2008年8月12日在广东火箭引雷试验中对220V架空民用线感应电压进行了观测。试验布置如下：两根水平架空导线长 1 500m，高 3m，引流杆距导线垂直距离约 40m且距导线一端（A端）约为1 250m，观测点距 A端约 1 300m。本文采用两个Heidler函数叠加拟合首次回击基电流，如图7。采用本文方法对观测点感应电压进行仿真计算,图8为本文仿真计算感应电压与实测结果相对比。

图7 回击通道底部电流Fig.7 Base current waveform of the return channel

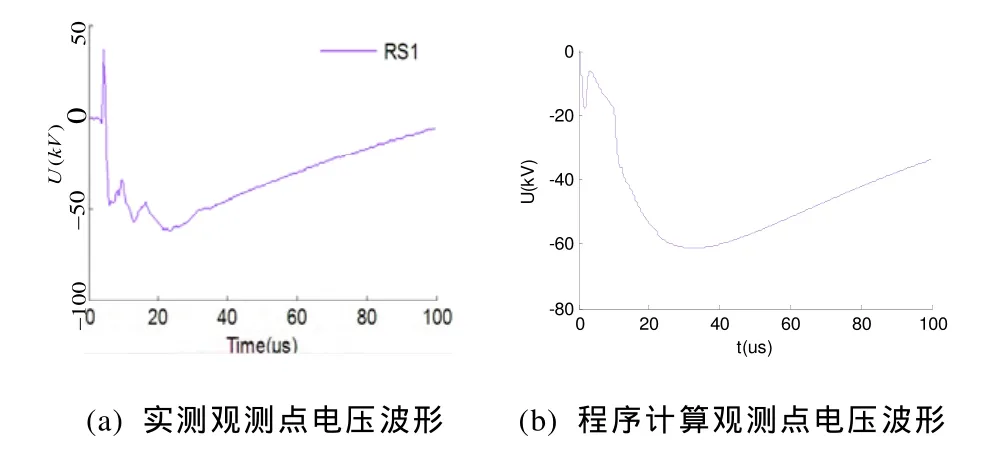
图8 观测点感应过电压Fig.8 Induced over-voltage of observation point

2 数值计算与自然闪电观测结果对比

2008年7月31日在上述观测系统中测得了由自然闪电引起的感应电压。在记录的1秒钟内共有7次回击过程，本文对第三次回击的观测点电压波形进行数值模拟，图9为实测电压波形和数值计算电压波形对比结果。

图9 观测点感应过电压Fig.9 Induced over-voltage of observation point

由以上两算例可见，本文多阶FDTD法计算观测点雷电感应过电压结果与实测数据吻合较好，证明该计算方法的正确性。

5 计算方法应用

本文多阶FDTD法可计算不同导线数在多工况下的雷电感应过电压。为检验该方法的计算性能，对雷电流部分参数和两种导线排布方式的影响进行计算分析。

5.1 雷电流幅值Im的影响

以图1所示简单结构为计算基础。模型参数设置为：单架空线长600m高3m，雷击点距线路垂直距离 50m且与线路两端距离相等，观测点距一端400m。采用 Heidler函数拟合基电流，采用 MTLL回击模型，大地电导率σ取5×10-3S/m。

基电流波形及回击参数相同，基电流幅值Im取值分别为11kA、16kA和21kA，所对应的观测点电压Um1、Um2和Um3的波形如图10所示。

图10 基电流幅值的影响Fig.10 The influence of base current amplitude

由图10可知，雷电流幅值 Im对线路感应电压的影响主要体现在幅值变化，Im从 11kA增大到16kA和21kA，提高比例分别为45%和91%，对应观测点感应电压幅值从20kV提高到32kV和45kV，提高比例分别为60%和125%。可见Im的提高明显引起了感应电压幅值提高，该过程对电压波形影响很小。

5.2 雷电流波头陡度的影响

基电流幅值及回击参数相同，其他输入设置同5.1，波头时间分别为 0.1μs、0.4μs和 1μs，所对应的观测点感应电压如图11。

图11 基电流波头陡度的影响Fig.11 The influence of base current wave steepness

由图11可知，雷电流波头陡度降低，波头时间从0.1μs增大到0.4μs和1μs，对应的感应电压幅值从 39kV降低到38kV和 35kV，降低比例为 3%和10%，波头时间从 1.8μs增大到 2.0μs和 2.5μs，分别增大11%和39%。可见雷电流波头陡度降低，引起了感应电压波头时间较明显增大，陡度降低，而幅值则降低很小。

5.3 导线排布方式影响

基电流和回击参数相同，三根架空导线水平布置(与雷击点距离分别为 50m、51m 和 52m，高度3m)和垂直布置（与雷击点距离 50m，高度分别为3m、4m和5m）时各导线观测点电压波形如图12。

由图12可知，水平排布的导线观测点感应电压幅值均为30kV左右，相差不足3%；而垂直排布的导线观测点感应电压则相差明显，由下而上分别约为30kV、45kV和60kV，中间和最高导线比最低导线分别提高了 50%和 100%。可见两种排布方式的“屏蔽效应”差异大，垂直排布的导线感应电压幅值差明显高于水平排布。两种排布方式对感应电压波形影响不大。

图12 导线排布方式的影响Fig.12 The influence of conductor configuration

6 结论

提出一种多阶FDTD的架空线雷电感应过电压计算方法，该方法采用一阶FDTD计算LEMP，采用二阶 FDTD推导场线耦合方程，比单纯的一阶FDTD法数值稳定性更高，得到结论如下：

1）与火箭引雷试验和自然闪电观测数据对比验证了所提方法的正确性和实用性。该方法可实现不同导线数在各种工况下雷电感应过电压的准确计算，且能更简捷的处理线路上的不连续点。

2）通过计算得到：雷电流幅值对线路感应电压幅值影响明显，对电压波形影响小；雷电流波头陡度对感应电压幅值影响较小，但对波形有较大影响。多导线之间有“屏蔽效应”，该效应受导线排布方式影响明显，垂直排布的导线感应电压差较水平排布明显要大。

[1] 李瑞芳,吴广宁,曹晓斌,等.雷电流幅值概率计算公式[J].电工技术学报,2011,26(4): 161-167.Li Ruifang,Wu Guangning,Cao Xiaobin,et al.Formula for probability of lightning current amplitude[J].Transctions of China Electrotechnical Society,2011,26(4): 161-167.

[2] 熊小伏,方伟阳,程韧俐,等.基于实时雷击信息的输电线强送决策方法[J].电力系统保护与控制,2013,41(19): 7-11.Xiong Xiaofu,Fang Weiyang,Cheng Renli,et al.Forced power supply decision of transmission lines based on real-time lightning information[J].Power System Protection and Control,2013,41(19): 7-11.

[3] 李瑞芳,吴广宁,曹晓斌,等.输电线路雷电绕击率的三维计算方法[J].电工技术学报,2009,24(10):134-138.Li Ruifang,Wu Guangning,Cao Xiaobin,et al.Three-Dimensional Calculation Method on Shielding Failure Rate of Transmission Lines[J].Transctions of China Electrotechnical Society,2009,24(10): 134-138.

[4] 谷定燮.500kV输变电工程设计中雷电过电压问题[J].高电压技术,2000,26(6): 60-62.Gu Dingxie.The Research on Lightning Overvoltages of 500kV Transmission Engineering Desgn[J].High Voltage Engineering,2000,26(6): 60-62.

[5] 周诗健,孙景群译.雷电/上下卷[M].北京: 水利电力出版社,1982.R.H.Golde.Lightning[M].Zhou Shijian,Sun Jingqun translated.Water Resources and Electric Power Press,1982.

[6] 冯雷,周佩白.高层建筑遭受雷击时感应电场的计算[J].高电压技术,2001,27(1): 52-54.Feng Lei,Zhou Peibai.Computation of the Induced Electric Field in a High Building[J].High Voltage Engineering,2001,27(1): 52-54.

[7] C.A.Nucci,F.Rachidi,M.V.Ianoz,et al.Lightning induced voltages on overhead lines.IEEE Trans.Electromag.Compat,1993,35(1): 75-83.

[8] V.Cooray.Effects of propagation on the return stroke radiation fields.Radio Sci,1987,22: 757-768.

[9] V.Cooray.Some consideration on the “Cooray-Rubinstein” formulation used in deriving the horizontal electric field of lightning return strokes over finitely conducting ground.IEEE Trans.Electromg.Compat.2002,44(4): 560-565.

[10] 边凯,陈维江,李成榕,等.架空配电线路雷电感应过电压计算研究[J].中国电机工程学报,2012,32(31): 191-199.Bian Kai,Chen Weijiang,Li Chengrong,et al.Calculation of lightning induced overvoltage on overhead distribution lines[J].Proceedings of the CSEE,2012,32(31): 191-199.

[11] K.S.Yee.Numerical solution of initial boundary value problems involving Maxwell equations in isotropic media.IEEE Trans.Antennas Propagat.1966,14(3): 302~307.

[12] He-Ming Ren,Bi-Hua Zhou,Vladimir A.Rakov et al.Analysis of Lightning-Induced Voltages on Overhead Lines Using a 2-D FDTD Method and Agrawal Coupling Model[J].IEEE Trans on Electromagnetic Compativility,2008,50(3): 651-659.

[13] M.Paolone.Lightning Electromagnetic Field Coupling to Overhead Lines: Theory,Numerical Simulations,and Experimental Validation [J].IEEE Transactions on Electromagnetic Compatibility,2009,51(3): 532-547.

[14] R.H.Golde.Lightning surges on overhead distribution lines caused by indirect and direct lightning strokes[J].Trans.Amer.Inst.Elec.Engrs.,1954,73,437-447.

[15] Heidler F,Cvetic J M,Stanic B V.Calculation of lightning current parameters[J].IEEE Transactions on Power Delivery,1999,14(2): 399-404.

[16] V.Cooray.On the concepts used in return stroke models applied in engineering practice.IEEE Transactions on Electromagnetic Compatibility,2003,45(1):101-108.

[17] C.D.Taylor,R.S.Satterwhite,C.W.Harrison,et al.The response of a terminated two-wire transmission line excited by a nonuniform elecromagnetic field[J].IEEE Trans.Electromagn.Compat,1965,13(6):987-989.

[18] A.K.Agrawal,H.J.Price,S.H.Gurbaxani.Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field[J].IEEE Transactions on Electromagnetic Compatibility,1980,22(2):119-129.

[19] F.Rachidi.Formulation of field-to-transmission line coupling equations in terms of magnetic excitation Field[J].IEEE Transactions on Electromagnetic Compatibility,1993,35(3): 404-407.

[20] 葛德彪,闫玉波.电磁波时域有限差分法(第三版)[M].西安: 西安电子科技大学出版社,2011:29-31.Ge Debiao,Yan Yubo.Finite-difference time-domain method for electromagnetic waves[M].Xian: xidian university press,2011: 29-31.

[21] M.Miki,V.A.Rakov.et al.Electric fields near triggered lightning channels measured with Pockels sensors.J.Geophys.Res.,2002,107: 10.1029/2001JD001087.