超磁致伸缩换能器预应力优化设计方法研究*
蔡万宠, 冯平法, 郁鼎文
(清华大学精密超精密制造装备及控制北京市重点实验室 北京, 100084)
超磁致伸缩换能器预应力优化设计方法研究*
蔡万宠, 冯平法, 郁鼎文
(清华大学精密超精密制造装备及控制北京市重点实验室 北京, 100084)
为优化超磁致伸缩换能器的工作性能、提高输出振幅,基于预应力对磁致伸缩效应的作用机理,建立了饱和磁致伸缩系数与预应力的关系模型。提出磁致伸缩灵敏度的概念,建立其与预应力和外磁场强度之间关系的理论模型。以超声换能器输出振幅最大为目标,提出以磁致伸缩平均灵敏度最大为准则的最佳预应力值确定方法。实验结果表明:随着预应力的增大,磁致伸缩平均灵敏度存在极大值,该预应力可在一定驱动磁场强度下获得最大的超声振幅,由此验证了磁致伸缩灵敏度模型的正确性和最佳预应力确定方法的可行性。提出的最佳预应力模型对超磁致伸缩换能器设计中预应力的选择具有指导意义,有助于大振幅超磁致伸缩换能器的设计及应用。
超磁致伸缩换能器;预应力;磁致伸缩灵敏度;振幅
引 言
旋转超声加工在硬脆难加工材料领域表现出特殊的优势,超声频机械振动可以有效提高高硬度、大脆性材料的加工效率和加工表面完整性[1-4]。超磁致伸缩材料(giant magnetostrictive material, 简称GMM)具有磁致伸缩系数大、功率容量高和响应速度快等优点,已成为超声换能器致动材料的新研究点[5-6]。超磁致伸缩材料的振动特性与其所受的预应力和偏置磁场大小有密切关系,合适的预应力可以提高材料的磁致伸缩系数,增大一定幅值交变磁场驱动下的超声振幅,是大功率超磁致伸缩换能器的研究重点[7]。Calkins等[7]通过实验得到了不同预应力下超磁致伸缩材料的磁致伸缩曲线,提出了最佳偏置磁场强度的确定方法。Bomba等[8]对不同预应力和温度条件下的超磁致伸缩换能器的磁致伸缩特性及能量损耗特性进行了实验研究,表明预应力对磁致伸缩系数和磁致伸缩能量损耗有显著影响。Dapino等[9]建立超磁致伸缩换能器的磁机耦合模型,研究了应力场和磁场的耦合相互作用。
目前,实际应用中关于预应力的确定方法一般根据经验选择,缺少相应的理论依据。为确定最佳预应力,得到一定外磁场强度下的最大振幅输出,提高超声换能效率,笔者分析了预应力对超磁致伸缩材料饱和磁致伸缩系数的作用机理,得到预应力对饱和磁致伸缩系数的影响规律。建立磁致伸缩灵敏度的数学模型,推导出磁致伸缩灵敏度是预应力的单值函数,提出以磁致伸缩平均灵敏度最大化为目标的最佳预应力值确定方法,以获得一定大小驱动磁场强度下的最大振幅输出。通过实验得到不同预应力下的磁致伸缩曲线,并拟合得到磁致伸缩平均灵敏度与预应力的关系模型,验证了最佳预应力确定方法的可行性。
1 预应力对饱和磁致伸缩系数和磁致伸缩位移灵敏度的作用机理
1.1 饱和磁致伸缩系数模型

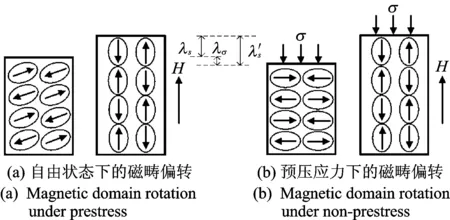
图1 预应力作用下饱和磁致伸缩系数的变化机理Fig.1 Variation of saturation magnetostriction coefficient with prestress
在一定预应力范围内,超磁致伸缩材料的饱和磁致伸缩系数是预应力的函数,如式1所示。
(1)
其中:λmax为GMM材料的极限磁致伸缩系数;σ0为使磁畴的磁化强度方向全部朝垂直于轴线方向排列的临界预应力。
当预应力小于σ0时,材料的饱和磁致伸缩系数将随着预应力的增大而提高。当预应力大于σ0时,随着预应力增大,饱和磁致伸缩系数保持不变。此外,过大的预应力将导致磁畴偏转所需的能量提高,减小在一定外磁场强度驱动下的磁致伸缩位移,因此,预应力数值存在最优值。
1.2 磁致伸缩灵敏度模型
由压磁效应可知,当超磁致伸缩材料受到压应力作用时,材料内部产生磁弹性能Eσ,使磁畴磁化方向偏离压应力方向,导致磁导率μ减小。铁磁性材料的相对磁导率变化率与应力的关系[11]为
(2)
其中:Bs为饱和磁感应强度;λs为饱和磁致伸缩系数。
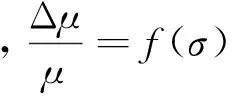
μ=μ(σ)
(3)
磁化率χ与相对磁导率的关系式为
μ=1+χ
(4)
磁化强度与外磁场强度的关系式为
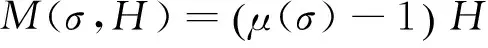
(5)
其中:M为磁化强度;H为外磁场强度。
根据磁致伸缩系数与磁化强度的关系[9](如式(6)所示),得到一定磁化强度引起超磁致伸缩材料的形变量。综合考虑模型的准确性和计算量,这里取i=2,即截取4次多项式表征磁致伸缩系数与磁化强度的关系,如式(7)所示。
(6)
λ(M)=γ1M2+γ2M4
(7)
其中:γ1,γ2可通过实验得到,并通过拟合方式建立具体的磁致伸缩系数与磁化强度之间的数学模型。
将式(5)代入式(7),得到磁致伸缩系数与预应力及外磁场强度的关系
(8)
得到压磁系数q与磁化率和外磁场强度的关系模型为
(9)
其中:q为压磁系数。
由式(9)可知,在一定的外磁场强度下,压磁系数为预应力的函数。
为量化单位磁场强度激励下超声换能器的磁致伸缩位移大小,定义磁致伸缩灵敏度ξ为超磁致伸缩换能器在单位外磁场强度驱动下输出的磁致伸缩位移
(10)
其中:ξ为磁致伸缩灵敏度;l1为超磁致伸缩材料的长度。
由式(10)可见,在一定的外磁场强度下,磁致伸缩灵敏度是预应力的单值函数,通过选择合适的预应力,可以得到最大的磁致伸缩灵敏度,从而在一定幅值的驱动磁场激励下获得最大的磁致伸缩位移输出。
综合分析式(1)和式(10)可知,饱和磁致伸缩系数和磁致伸缩灵敏度同为预应力的函数,在一定预应力范围内,随着预应力的增大,饱和磁致伸缩系数提高,但不直接决定超声换能器在一定驱动磁场下的振幅大小。为提高超声换能器的振幅,应以磁致伸缩灵敏度最大化为目标确定预应力,以该预应力下的磁致伸缩曲线线性段的中点作为偏置磁场大小,使超磁致伸缩材料在交变磁场激励下工作在磁致伸缩灵敏度最大的线性区域,从而获得最大的超声振幅。
2 实验验证
为验证磁致伸缩灵敏度模型的正确性及最佳预应力确定方法的可行性,对超磁致伸缩换能器在不同预应力条件下的磁致伸缩曲线进行了实验研究,并计算得到不同预应力下的磁致伸缩灵敏度。图2为实验原理图。利用压力传感器BSYP-2测量超磁致伸缩材料所受预应力,并将其转换成电压信号;激光位移传感器测量换能器输出端的位移变化,由式(11)计算磁致伸缩系数λ。信号发生器与功率放大器构成直流电源,实验中通过改变电流调整GMM所处空间的磁场强度,激励电流的调节范围为0~11A,示波器实时测量超声换能器励磁线圈中的电流。
(11)
其中:xH为外磁场强度H作用下的输出端坐标;x0为输出端初始坐标。

图2 实验原理图Fig.2 Principle sketch of the experiment
2.1 超磁致伸缩换能器的设计
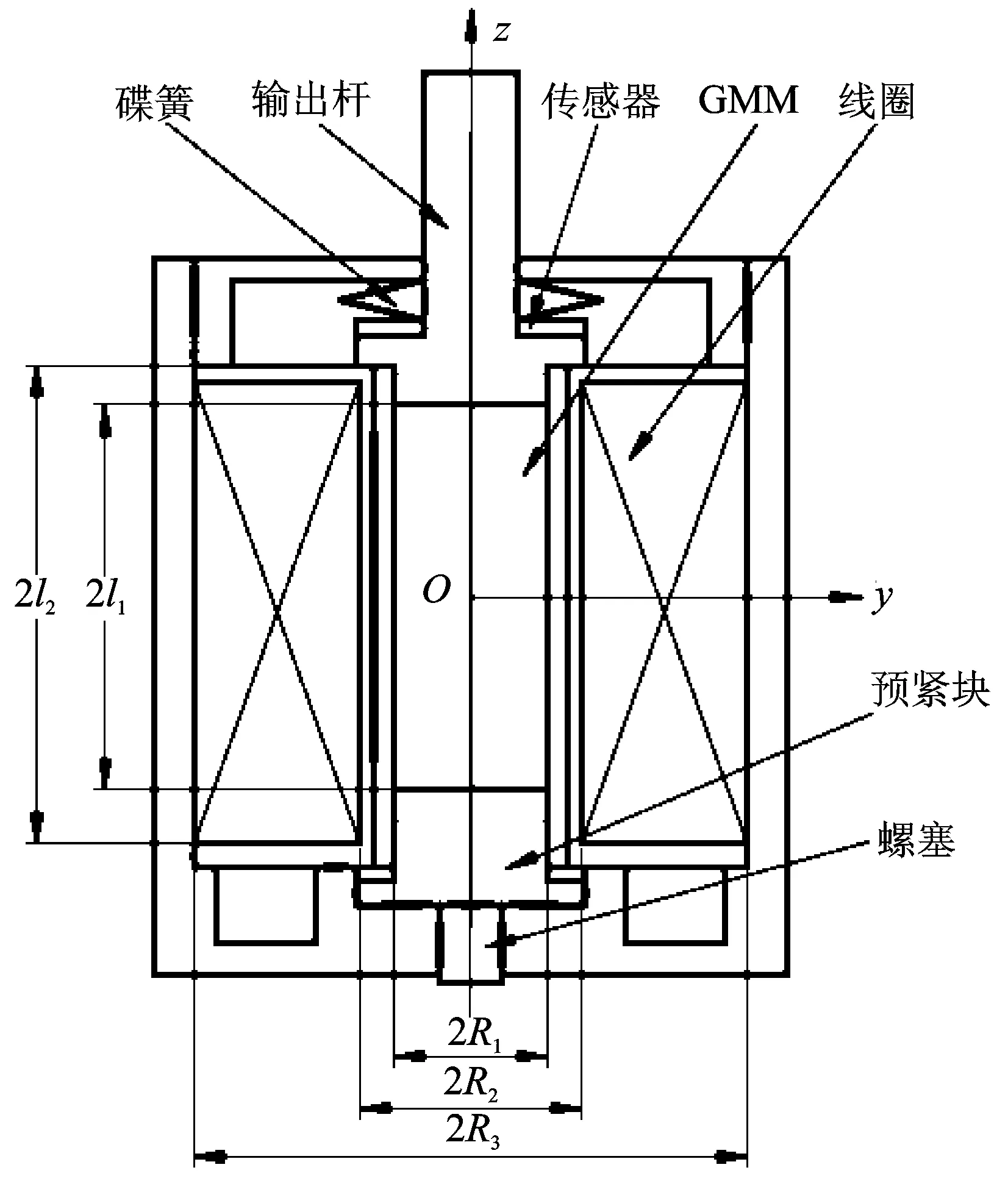
图3 超磁致伸缩换能器结构示意图Fig.3 Structure sketch map of giant magnetostrictive transducer
图3所示的超磁致伸缩换能器由超磁致伸缩材料Terfenol-D、线圈骨架、线圈、碟簧、输出杆、预紧块和螺塞等组成。为减小涡流效应对超磁致伸缩换能器振动特性的影响,GMM采用切片结构。预应力由碟簧施加,改变碟簧形变量得到不同预应力。由式(12)计算磁致伸缩振动引起的碟簧预紧力变化量,经对比分析,磁致伸缩振动引起的预紧力变化量远小于预应力,因此可近似取预应力为超磁致伸缩换能器工作过程中GMM所受的应力。超磁致伸缩材料和励磁线圈的结构参数如表1所示。
(12)
其中:F为碟簧预紧力;E为弹性模量;t为碟簧厚度;μ为泊松比;K1为计算系数,查机械设计手册可得;D为碟簧外径;h为碟簧锥高。

表1 超磁致伸缩换能器的结构参数
2.2 驱动磁场强度的计算
超磁致伸缩换能器所需的激励磁场通常由通电线圈产生,线圈的结构和尺寸是影响激励磁场强度的主要因素,如图3所示。笔者的研究重点为预应力对磁致伸缩效应的影响,因此忽略通电线圈在GMM所处空间产生磁场的不均匀性,以线圈轴线上的磁场强度表征GMM所受驱动磁场强度,外磁场强度[12]为
(13)
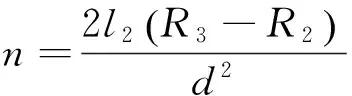
由式(13)可知,当超声换能器的结构参数一定时,GMM内外磁场强度与电流成正比。因此,可通过改变线圈中的电流来改变超磁致伸缩材料所处空间的磁场强度。
2.3 不同预应力下的磁致伸缩曲线
当预应力在0~14MPa范围内变化时,超磁致伸缩换能器在相同的外磁场强度下表现出不同的磁致伸缩效应。如图4所示,分别对超磁致伸缩换能器在不同预应力条件下的磁致伸缩曲线进行测量,计算得到不同磁场强度下磁致伸缩系数随预应力的变化曲线,如图5所示。实验结果表明:
1) 在一定范围内,随着预应力的增大,GMM的磁致伸缩系数显著增大,当外磁场强度较大时,预应力对磁致伸缩系数的影响更显著。由于预应力使磁畴垂直于超磁致伸缩棒轴向偏转,因此适当的预压应力可以提高超磁致伸缩换能器在相同的驱动磁场下的磁致伸缩位移。
2) 当保持外磁场强度不变时,随着预应力的增大,磁致伸缩系数先增大后减小。由此可知,预应力并非越大越好,存在最佳预应力使输出振幅最大。
3) 磁致伸缩系数随着外磁场的增大呈近线性增长,当外磁场强度较小时,磁致伸缩曲线存在“死区”。在“死区”范围内,单位外磁场引起的磁致伸缩位移较小,可通过施加适当大小的偏置磁场使换能器的工作区间避开磁致伸缩曲线的“死区”范围。
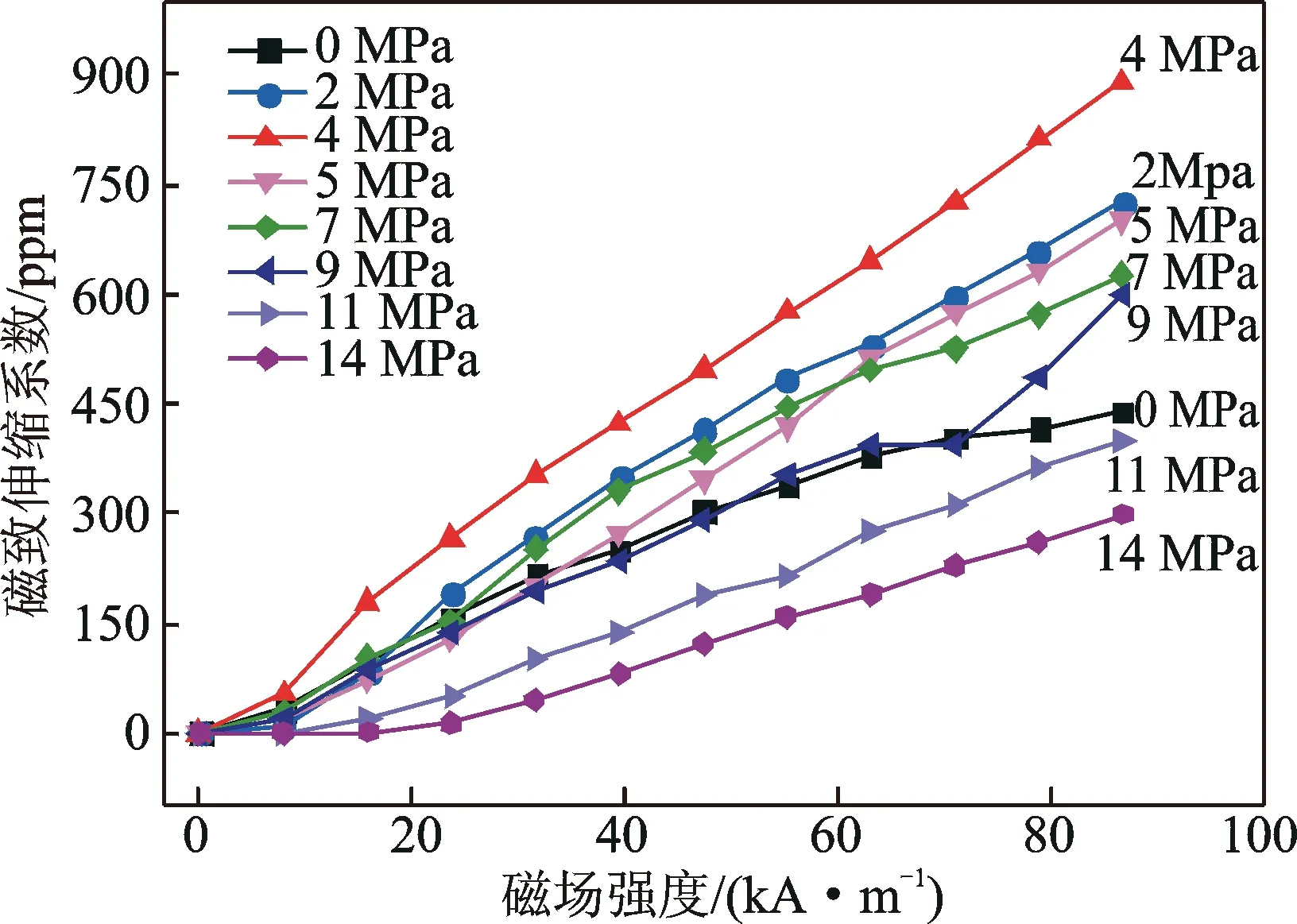
图4 不同预应力作用下的磁致伸缩曲线Fig.4 Magnetostrictive curves of GMM with different prestress

图5 不同磁场强度下磁致伸缩系数随预应力的变化曲线Fig.5 Relation of magnetostrictive coefficient and prestress with different magnetic field intensities
2.4 不同预应力下的磁致伸缩灵敏度
为研究不同预应力大小下超声换能器磁致伸缩位移灵敏度的变化规律,根据式(9)和式(10)得到不同磁场强度下的磁致伸缩灵敏度。不考虑磁致伸缩“死区”范围,计算得到不同预应力条件下,超声换能器的磁致伸缩平均灵敏度为
(14)
其中:ξ′为平均磁致伸缩灵敏度;ξi为激励电流大小为i时的磁致伸缩灵敏度.
图6为磁致伸缩平均灵敏度随预应力变化的散点图。由式(10)可知,磁致伸缩灵敏度可表示为预应力的函数。用origin进行多项式拟合,建立磁致伸缩平均灵敏度与预应力之间关系的拟合曲线,如图6所示。拟合多项式为
ξ(σ) =2.608×10-4+1.266×10-4σ-2.226×
10-5σ2+1.15×10-6σ3-1.684×10-8σ4
(15)
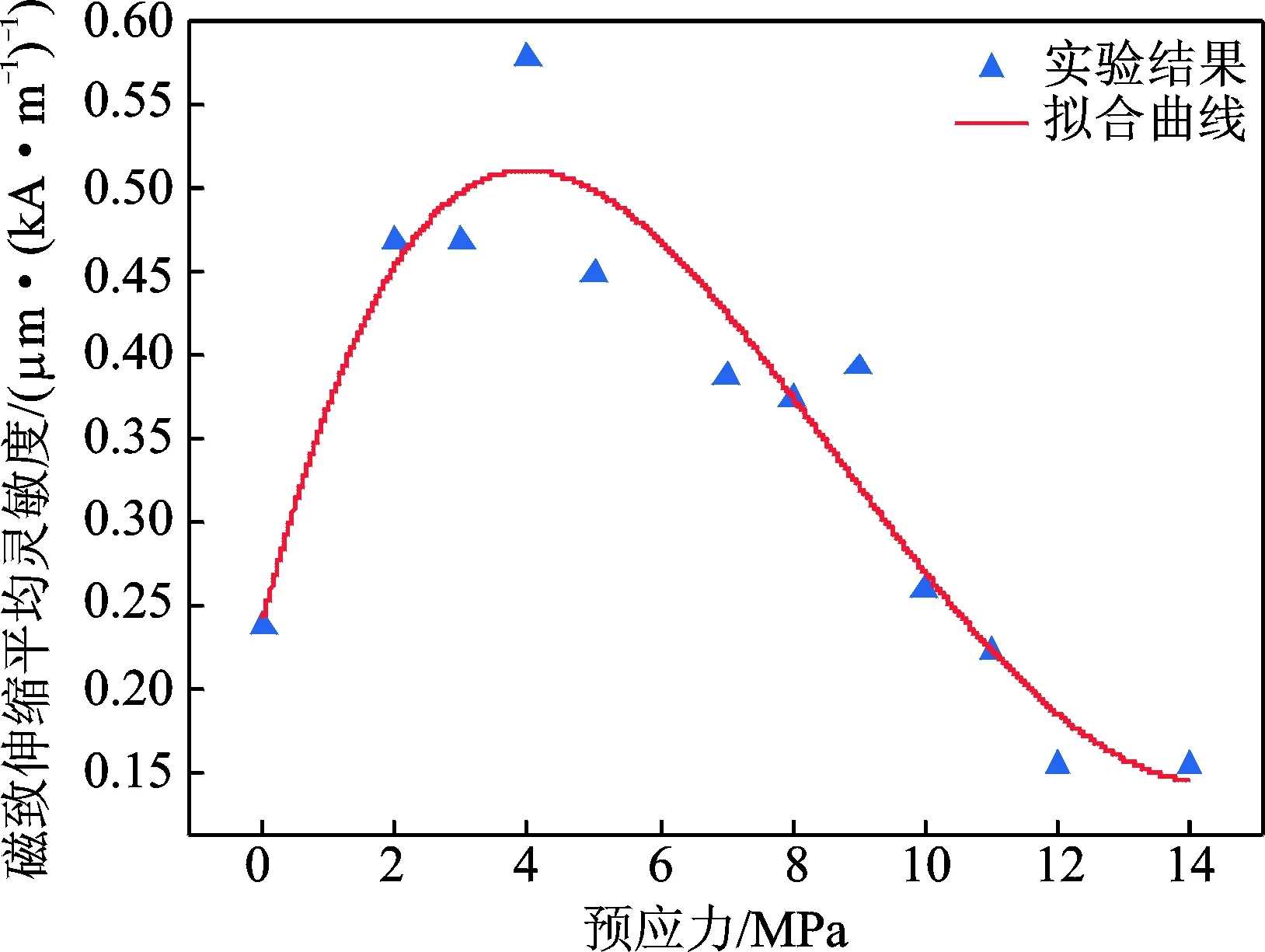
图6 磁致伸缩位移平均灵敏度与预应力的关系Fig.6 Relation of the average magnetostrictive sensitivity and prestress
多项式拟合得到的磁致伸缩平均灵敏度残量值较小,所有预应力下的残量大小都在±0.06范围内,四次多项式拟合可较好地表征磁致伸缩平均灵敏度随预应力的变化规律。实验数据及拟合曲线表明:
1) 多项式拟合曲线与实验数据能够较好的吻合,证明磁致伸缩灵敏度模型的正确性。
2) 随着预应力增大,超声换能器的磁致伸缩灵敏度先增大后减小,存在极值点,即预应力存在最优值。因此,以磁致伸缩平均灵敏度的极值点所对应的预应力为最佳值,可得到最大超声振幅输出。
根据上述预应力确定原则,笔者设计的超声换能器的最佳预应力为3.97MPa。
为验证最佳预应力的正确性,实验得到超磁致伸缩换能器在3.97MPa预应力作用下的磁致伸缩曲线,其与4MPa预应力作用下的磁致伸缩曲线基本重合,且磁致伸缩平均灵敏度为0.535μm/(kA·m-1)。对比图6可知,3.97MPa预应力作用下的磁致伸缩平均灵敏度取得极大值,由此可证明最佳预应力的正确性。
3 结 论
1) 随着预应力的增大,相同外磁场强度下的磁致伸缩系数先增大后减小,当预应力大于使所有磁畴方向都朝垂直于外磁场方向偏转的临界预应力值时,预应力将阻碍磁畴向外磁场方向偏转,磁致伸缩系数减小。
2) 为提高单位外磁场强度下的磁致伸缩位移,提出磁致伸缩灵敏度的概念。基于预应力对超磁致伸缩材料磁导率μ的影响,推导出磁致伸缩灵敏度的数学模型,并通过实验验证了磁致伸缩灵敏度模型的正确性。
3) 根据磁致伸缩平均灵敏度模型,用四次多项式拟合磁致伸缩平均灵敏度与预应力的关系。在一定驱动磁场下,磁致伸缩平均灵敏度是预应力的单值函数,随着预应力的增大,磁致伸缩平均灵敏度先增大后减小,存在极大值,说明以磁致伸缩平均灵敏度最大化为原则的最佳预应力确定方法的可行性。
4) 提出了一种适用于超声换能器的最佳预应力确定方法,可在一定的外磁场驱动下得到最大振幅输出,对大振幅超声换能器的预应力确定具有指导意义。
[1] Kadivar M A, Akbari J, Yousefi R, et al. Investigating the effects of vibration method on ultrasonic-assisted drilling of Al/SiCp metal matrix composites[J]. Robotics and Computer-Integrated Manufacturing, 2014,30(3): 344-350.
[2] Bertsche E, Ehmann K, Malukhin K. An analytical model of rotary ultrasonic milling[J]. The International Journal of Advanced Manufacturing Technology, 2013, 65(9-12): 1705-1720.
[3] 曾庚鑫, 曹彪, 曾海泉. 超磁致伸缩功率超声换能器的振动分析[J]. 振动、测试与诊断, 2011, 31(5): 614-617.
Zeng Gengxin, Cao Biao, Zeng Haiquan. Vibration analysis on magnetostrictive power ultrasonic transducer [J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(5): 614-617.(in Chinese)
[4] 张承龙, 冯平法, 吴志军. 旋转超声加工振幅与实际切削深度特性研究[J]. 兵工学报, 2013, 34(7): 883-888.
Zhang Chenglong, Feng Pingfa, Wu Zhijun. Research on the properties of ultrasonic vibration amplitude and actual cutting depth in rotary ultrasonic machining[J]. Acta Armamentarii, 2013, 34(7): 883-888.(in Chinese)
[5] 袁惠群, 李莹, 李东,等. 超磁致伸缩微致动器车削系统建模与控制[J]. 振动、测试与诊断, 2014, 34(2): 351-355.
Yuan Huiqun, Li Ying, Li Dong, et al. Modelling and control for giant magnetostrictive micro-actuator turning system[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(2): 351-355.(in Chinese)
[6] Weisensel G N, Hansen T T, Hrbek W D. High-power ultrasonic Terfenol-D transducers enable commercial applications[C]∥5th Annual International Symposium on Smart Structures and Materials.[S.l.]:International Society for Optics and Photonics,1998: 450-458.
[7] Calkins F T, Dapino M J, Flatau A B. Effect of prestress on the dynamic performace of a terfenol-d transducer[C]∥Smart Structures and Materials.[S.l.]:International Society for Optics and Photonics, 1997: 293-304.
[8] Bomba J, Kaleta J, Sawa P. An initial investigation into change in magnetomechanical properties of terfenold rod due to prestress and temperature[J]. Anyagvizsgalok Lapja, 2004 (1): 19-21.
[9] Dapino M J, Smith R C, Faidley L A E, et al. A coupled structural-magnetic strain and stress model for magnetostrictive transducers[J]. Journal of Intelligent Material Systems and Structures, 2000, 11(2): 135-152.
[10]近角聪信. 铁磁性物理[M]. 葛世慧, 译. 兰州: 兰州大学出版社,2002:408-415.
[11]郭沛飞, 贾振元, 杨兴,等. 压磁效应及其在传感器中的应用[J]. 压电与声光, 2001(1): 26-29.
Guo Peifei, Jia Zhenyuan, Yang Xing, et al. Magnetoelastic effect and its application in sensors[J]. Piezoelectrics & Acoustooptics, 2001(1): 26-29.(in Chinese)
[12]李明范, 项占琴, 吕福在. 超磁致伸缩换能器磁路设计及优化[J]. 浙江大学学报:工学版, 2006(2): 192-196.
Li Mingfan, Xiang Zhanqin, Lü Fuzai. Magnet circuit design and optimization of giant magnetostrictive transducer[J]. Journal of Zhejiang University: Engineering Science, 2006(2): 192-196.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.01.007
*国家自然科学基金资助项目(51475260);北京市自然科学基金资助项目(3141001)
2015-01-26;
2015-04-22
TG663; TH89
蔡万宠,男,1991年3月,博士生。主要研究方向为超磁致伸缩旋转超声加工系统设计理论与加工机理。 E-mail:cwcfengdou@163.com 通信作者简介: 冯平法,男,1966年2月生,教授、博士生导师。主要研究方向为超声与高速精密加工工艺与装备、制造装备性能分析与优化设计。 E-mail:fengpf@mail.tsinghua.edu.cn

