基于逆有限元的应变模态损伤检测方法*

杨海峰， 吴子燕， 孙 蓬， 张 坤

(1.西北工业大学力学与土木建筑学院 西安，710129) (2.西北工业大学计算机学院 西安，710129)

基于逆有限元的应变模态损伤检测方法*

杨海峰1， 吴子燕1， 孙 蓬2， 张 坤1

(1.西北工业大学力学与土木建筑学院 西安，710129) (2.西北工业大学计算机学院 西安，710129)

基于光纤光栅传感器(fiber Bragg grating,简称FBG)逆有限元方法(inverse finite element method,简称iFEM)，仅利用有限测点的应变数据进行全域应变场重构，得到近似完全测量应变模态，提高了直接采用实测应变数据来构建应变模态损伤指标的实用性。利用基于损伤应变模态差分原理的损伤指标法，只需用损伤后应变模态数据即能定位损伤，并给出了损伤指标数学模型。计算结果表明，基于光纤光栅传感器和逆有限元方法可以快速进行全域应变场重构，为基于应变模态的损伤检测提供数据保障，而应变模态差分曲线只在损伤处发生剧烈变化，损伤程度不同，曲线突变程度略有不同但规律一致。最后以某板的实验结果证明了该方法的有效性。

逆有限元法；损伤检测；应变模态；光纤光栅传感器

引 言

结构损伤识别作为结构健康监测系统的核心内容，在航空航天、机械和土木工程等领域得到应用。由于实际结构的早期微小损伤不容易被检测出来，会对结构的安全性与可靠性产生影响，甚至引发重大事故。通常结构损伤会引起模态参数的变化，国内外学者提出了很多识别损伤的指标，如固有频率、振型、位移类模态参数(模态柔度、位移、位移模态)和应变类模态参数(曲率模态、应变、应变模态)等[1-4]。

已有大量研究表明，固有频率仅能识别损伤是否存在,而不能识别其位置和程度。模态柔度对单损伤有较好的识别能力，但对多损伤效果不明显。位移模态仅能识别损伤位置和总体的损伤程度，但不能识别局部损伤程度。应变模态对损伤识别优于位移模态，特别是在结构局部应力集中或裂纹检测时，它能获得结构的动应变，且应变值只在损伤附近变化明显，远离损伤处改变不大。

采用应变模态至少有两方面的好处，其一是可免去由位移到应变计算过程中所带来的误差，而这种误差往往是很难控制的。因为由位移到应变是微分过程，位移的微小改变将被放大，从而引起应变参数的显著变化。因此，应变类参数(应变模态和曲率模态)对结构局部微小损伤反应较敏感，而位移模态对此反应甚微。其二是可直接研究某些关键部位的应变，如应力集中问题和局部结构变动对附近受力情况的影响等。

应变类损伤指标大多需要利用损伤前后的模态数据。实际上，由于设计资料不全、施工离散性和材料劣化等问题，要得到损伤前的精确状态非常困难。因此应变类损伤指标法在实际工程中尚难以推广应用[5]。为此，笔者利用光纤光栅传感器和逆有限元理论，提出基于逆有限元的应变模态损伤检测方法，仅利用有限测点的应变数据且无需损伤前的模态数据即可进行损伤检测。

1 基本理论

1.1 应变模态基本理论

应变是位移的一阶导数,对应于每一阶位移模态，必有其对应的固有应变分布状态，这种与位移模态相对应的固有应变分布状态称之为应变模态，它能反映结构的固有特征。设弹性结构的变形位移为u，ν和w，运用模态叠加进行应变εx推导

(1)

(2)

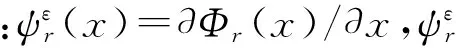
(3)

位移响应表示为

(4)

根据应力应变关系，得到应变响应表达式为

(5)

其中：εx，εy，εz为正应变；γxy，γyz，γzx为剪应变。

通常剪切应变无法直接测量，笔者将光纤光栅传感器按照应变花的形式布置，如图1所示，再利用平面应变理论推导出剪切应变。

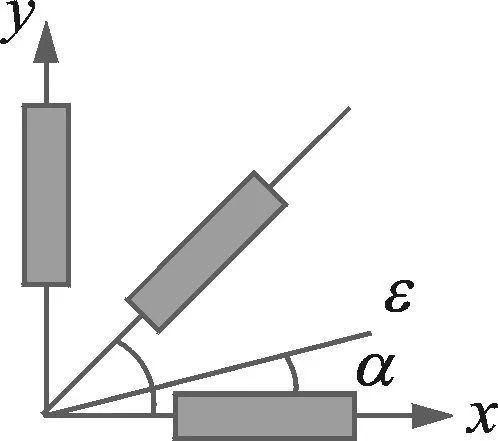
图1 光纤光栅传感器布置形式Fig. 1 Placement of fiber Bragg grating sensor

由平面应变状态几何关系分析可知

其中：εα和γα分别为α截面上的线(正)应变和切应变。

将α=45°代入式(6)，可得

(8)

γxy=εx+εy-2ε45°

(9)

按笔者方式贴放光纤传感器并结合式(9)，即可获得待测点的应变εx,εy和γxy。

1.2 损伤应变模态差分数学模型

(10)

其中：xi为节点i的坐标值。

设xi+1-xi=h，并假定h充分小，不计三次幂项及更高次幂项，等间距差分式为

(11)

曲线的变化程度通常利用导数反映，但在未归一化之前，各阶应变模态差分曲线数量级存在差异，没有可比性，此外还存在试验或计算误差等引起的突变假象问题，导致直接从差分曲线进行突变程度定量判定较为困难。为此引入有效极值点概念[6]：若差分曲线任意相邻两极值符号相异，则它们之间有且仅有一个零值点，该极值点称为有效极值点。

基于有效极值点定义的损伤位置指标数学模型为

(12)

其中：ID(j)为某阶应变模态差分曲线第j个有效零值点损伤位置指标值；xi,yi分别为差分曲线有效极值点与相应的极值；l为总体跨度尺寸。

该指标具有明确的位置坐标，且ID(j)值越大，损伤可能性越大，再结合差分曲线变化规律，即可判定损伤位置。

1.3 基于光纤光栅传感器和逆有限元的应变模态损伤识别

将应变模态指标应用于实际结构损伤检测，首先要解决测量手段问题。和传统的应变片相比，光纤光栅对应力应变变化非常敏感，测量精度也非常高，应变测量分辨率已达1 με，利用光纤光栅传感器复用技术还可同时测量多点应变，甚至埋入被测构件内部，实现构件内部应力应变测量[7-8]。

但若想获取未布置传感器区域的应力应变信息，以及区域内任一点的应力应变，要根据已知测点数据进行结构全域应力应变反演。在这个过程中，逆有限元法被证明是一种比较有效的方法。

离散应变测量值重构结构中每个结点的应变和位移属于逆数学问题。在不必要满足存在性、唯一性和稳定性的意义上，逆问题是不适定的。对于这类问题，通常的解法是基于正则化算子构建近似解，但此近似解只有在测量数据变化小的情况下是稳定的。Tessler等[9-11]基于有限元思想，结合变分原理，提出逆有限元法，其本质是首先根据传感器布局，对结构进行合理的有限元网格划分(划分方式与传感器布局有关，笔者采用均布方式)，然后利用实验测得的结构表面应变，选取合适的有限元形函数对单元进行反演推导，再将单元方程扩展至结构整体方程，由此实现仅利用有限测点数据进行结构全域应力应变反演。其变分公式基于对最小二乘泛函求最小值，且该泛函仅使用符合一阶线性剪切变形理论的应变测量数据。由于该公式容许横向剪切变形，因此适用于薄的及适中厚度的板壳结构。变分原理的主要好处是适用于具有C0连续性的有限单元离散化，因此可以将鲁棒性算法应用到复杂的民用和航空结构，特别适合针对下一代实时结构健康监测系统的使用。

运用逆有限元法进行结构全域应力应变场反演的主要理论推导过程如下。

首先，使用由Mindlin理论应变值和对应的应变测量值构成的最小二乘差分项构建误差泛函，其中Mindlin应变值以位移的形式表示。受惩罚参数控制的正则化项强迫其服从横向剪切应变的约束条件，由于这个设定，使所有应变协调关系自然明确地得到满足，所以该方法与材料的弹性和惯性特性无关[9]。

平板壳单元的变形按Mindlin理论中的位移向量定义为

(13)

其中：u=u(x,y),v=v(x,y)分别为中平面x和y方向上的位移；θx=θx(x,y)，θy=θy(x,y)分别为以x轴负方向和y轴正方向为法线的转角；w=w(x,y)为挠度变量，其沿厚度坐标z∈[-t,t]恒定不变；2t为板壳的总厚度。

应变位移关系式为

(14)

与中平面拉伸相关联的膜应变为

Leu

(15)

同理，弯曲曲率及横向剪切可分别写为k(u)≡Lku和g(u)≡Lgu。

图2 使用应变花测量板的上下表面应变Fig.2 Measurement of strain of using FBG strain flower

结构单元位移向量由最小二乘泛函取极值时获得，可表示为

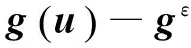
(16)

利用位移有限单元法，通过使用适当的形函数插值式(16)中的位移场，可得

(17)

其中：N为具有C0连续性的非等参形函数矩阵。

Keue=fe

(18)

其中：Ke仅为位置坐标的函数；fe为坐标和实测应变值的函数。

最后，通过标准有限单元集成操作，将离散的单元矩阵组装到整体线性方程系统中，即可实现位移自由度从单元局部坐标系到总体坐标系的转换。通过施加Mindlin位移边界条件，位移自由度解存在且唯一。一旦得到结点位移，可通过单元级别的简单计算得到平滑的单元应变。这些计算都基于线性方程，因此计算效率很高。

运用逆有限元方法进行全域反演之后，可获取近似完全测量的应变模态，解决了传统应变模态损伤指标需要完备的实测振型问题，大大提高直接采用测量数据构建应变模态损伤指标进行损伤检测的实用性。

2 算例及分析

以图3所示的悬臂板为例，对笔者提出的算法进行验证。板尺寸为65 cm×30 cm×0.68 cm，左端采用三点固定，材料弹性模量E=210 GPa，泊松比ν=0.3，测试仪器包括光纤传感器、光纤光栅波长解调仪等。损伤设置情况为在两个单元(1157号、809号)处的单元刚度分别降低20%和50%(如图4所示)，其位置(x,y)坐标分别为(51 cm×17 cm，28 cm×12 cm)。在距右端5 cm处(距上边缘10 cm)施加集中力P，采用悬挂标准砝码的方式施加激励，模拟集中作用力(实验所用的板右侧有一微孔可以吊装标准砝码荷载)。

图3 构件尺寸图(单位：cm)Fig.3 Size chart of plate(unit:cm)

图4 实验现场与有限元模型图Fig.4 Experimental field and finite element model (FEM)

首先，利用布置在板上的光纤传感器(每个测点为一组应变花)测得18个点的应变值；然后，利用逆有限元法进行结构全域应力应变反演与重构，以获取近似完全测量的应变模态，逆有限元法反演重构的挠度图以及损伤后的各阶应变模态如图5，6所示。

从图5可以看出，利用逆有限元法对悬臂板挠度的反演重构结果与有限元仿真软件计算的挠度结果非常接近(从数据上对比显示平均相对误差仅为1.73%，因数据量过多，此处未列出)，表明逆有限元法在全域反演方面具有非常好的效果。

通过逆有限元法反演可得到近似完全测量的应变模态，这是普通应变测量无法做到的。利用反演后的损伤应变模态数据计算三维应变差分结果及应变模态差分曲线结果如图7，8，9所示。应变模态差分曲线及损伤位置指标为曲线形式，因此只取经过损伤点的二维应变模态差分曲线上的数据进行计算。

图5 逆有限元法反演重构挠度与有限元软件数值分析结果Fig. 5 Deflection results of iFEM method and FEM software

图6 损伤后应变模态Fig. 6 Strain model shape before and after damage

图7 五阶应变模态的三维应变差分图Fig. 7 3D Strain difference diagram of order 5

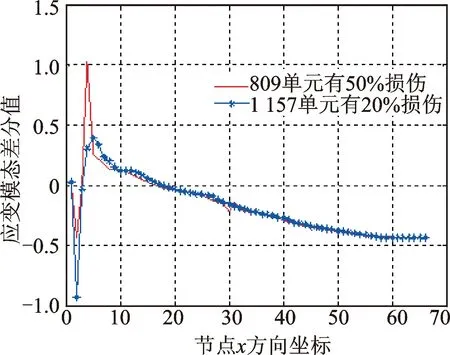
图8 第1阶应变模态差分曲线Fig.8 Strain modal difference curve of first order

图9 第3阶应变模态差分曲线Fig.9 Strain modal difference curve of third order

类别损伤程度20%50%1阶ID(1)18.457.60ID(2)26.8232.21ID(3)18.567.3ID(4)3.525.253阶ID(2)9.1110.81ID(3)30.1743.52ID(4)10.1211.33ID(5)22.866.23

黑体数字对应损伤位置

从图6可以看出，仅仅从应变模态图中很难发现损伤情况(应变模态图中左边界处的3个峰值是由于板的左端采用三点固定夹持方式导致)，在假设能够获取损伤前模态数据的前提下或许还可以利用损伤前后的数据对比分析来判断损伤情况，但在无法获取损伤前数据时，仅根据模态数据来分析损伤将非常困难。应变差分图中，虽然一阶模态差分曲线并不能明显看出损伤，但在三阶模态差分曲线中可以发现在损伤发生的位置曲线有明显的突变(由于噪声干扰及数据降噪处理后，20%损伤处的突变较小)。这也说明无论是单一损伤还是多个损伤，都可以在应变模态差分曲线中得到体现，表明笔者提出方法的有效性。

由图8，9还可知，在归一化之前，各阶应变模态差分数据的数量级相差悬殊，无法统一对比，只能借助归一化之后的损伤指标ID(j)进行分析。若某点在某阶或多阶ID值越大，损伤可能性越大。实际计算结果如表1所示，可以看出，各阶的损伤处ID值均为最大值(1阶的ID(2)和3阶的ID(3)，分别对应着刚度降低20%和50%的两处损伤位置)。节点处损伤可通过其余阶指标值ID(j)定位，再结合差分曲线变化规律判定出损伤位置。

3 结束语

基于光纤光栅传感器和逆有限元方法，利用有限测点的应变数据进行全域应变场重构，得到近似完全测量应变模态，解决了传统应变模态损伤指标需要完备的实测振型问题。利用基于损伤应变模态差分原理的损伤指标法，仅用损伤后的数据进行了损伤定位。计算结果表明，逆有限元法是根据已知测点数据进行结构全域应力应变反演比较有效的一种方法，通过逆有限元全域反演可得到近似完全测量的应变模态，这是普通应变测量无法做到的。还发现除支座附近外，应变模态差分曲线只在损伤处发生剧烈变化，损伤程度不同，突变程度略有不同但规律一致。悬臂板的实验结果也证明所提方法的有效性。

[1] Yan Yunju, Cheng Li, Wu Ziyan, et al. Development in vibration-based structural damage detection technique [J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2198-2211.

[2] Wu H. The challenges of structural health monitoring technologies in civil infrastructure [C]∥ 8th International Workshop on Structural Health Monitoring． Stanford, California：DEStech Publications, Inc., 2011.

[3] Pandey A K, Biswas M. Damage diagnosis of truss structures by estimation of flexibility change [J]. Modal Analysis, 1995, 10(2): 104-117.

[4] 周邵萍,郝占峰,韩红飞,等.基于应变模态差和神经网络的管道损伤识别[J]. 振动、测试与诊断, 2015, 35(2): 334-338.

Zhou Shaoping, Hao Zhanfeng, Han Hongfei, et al. Damage identification in straight pipeline using strain modal difference and neural network [J]. Journal of Vibration, Measurement & Diagnosis，2015,35(2):334-338. (in Chinese)

[5] 顾培英, 陈厚群, 李同春,等. 用应变模态技术诊断梁结构的损伤[J].地震工程与工程振动,2005,25(4):50-53.

Gu Peiying, Chen Houqun, Li Tongchun， et al. Application of strain mode in diagnosing damage to beam [J]. Earthquake Engineering and Engineering Vibration, 2005,25(4): 50-53.(in Chinese)

[6] 顾培英. 基于应变模态技术的结构损伤诊断直接指标法研究[D]．南京：河海大学，2006.

[7] 姜德生, 罗裴, 梁磊. 光纤布拉格光栅传感器与基于应变模态理论的结构损伤识别[J]. 仪表技术与传感器, 2003(2):17-19.

Jiang Desheng, Luo Pei, Liang Lei. Fiber Bragg grating sensor and recognition of structural damage based on strain modal theory [J]. Instrument Technique and Sensor, 2003(2): 17-19.(in Chinese)

[8] 柯孟龙. 基于光纤光栅传感和应变动力参数的损伤识别研究[D]. 武汉：武汉理工大学，2011.

[9] Tessler A. Structural analysis methods for structural health management of future aerospace vehicles[R].2007,NASA/TM-2007-214871.https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20070018347.pdf.

[10] Tondreau G, Deraemaeker A. Automated data-based damage localization under ambient vibration using local modal filters and dynamic strain measurements: experimental applications [J]. Journal of Sound and Vibration, 2014, 333(26): 7364-7385.

[11] Gherlone M, Cerracchio P, Mattone M, et al. Shape sensing of 3D frame structures using an inverse finite element method [J]. International Journal of Solids and Structures, 2012 (49): 3100-3112.

10.16450/j.cnki.issn.1004-6801.2017.01.023

*国家自然科学基金资助项目(51278420);中央高校基本科研业务费专项资金资助项目(3102015BJ(II)MYZ13); 西北工业大学研究生创意创新种子基金资助项目(Z2016094);西北工业大学基础研究基金资助项目(JCY20130125)

2015-11-23；

2016-05-31

O327;TH17

杨海峰，男，1976年9月生，博士。主要研究方向为结构健康监测与结构损伤检测。曾发表《基于MIGA算法的结构模型修正研究及其应用》(《振动、测试与诊断》2012年第32卷第2期)等论文。 E-mail: hfyang@nwpu.edu.cn