电弧炉电极调节系统的模糊解耦控制器

鲁 军 霍金彪 张广跃

电弧炉电极调节系统的模糊解耦控制器

鲁 军1霍金彪1张广跃2

（1. 沈阳理工大学信息科学与工程学院 沈阳 110159 2. 天津电气传动设计研究所有限公司检测中心 天津 300180）

由于电弧炉三个电极之间存在耦合作用，严重影响了三相电极的控制效果，而普通单相控制方法因未考虑耦合易出现较大的失调。本文在分析三相电极耦合关系基础上，推导出电流补偿解耦方法。该方法对电极解耦有理论意义，但补偿系数与弧长实时相关且计算量较大。故在电流补偿解耦方法基础上又引入了单输入双输出的模糊器进行补偿解耦。通过Matlab/Simulink软件对其解耦性、抗干扰性进行仿真并对现场采集的数据进行解耦前后的比较，结果表明模糊补偿解耦器能消除三相电极之间的强耦合作用，提高电弧炉炼钢效率及降低能耗。

电弧炉 三相耦合 解耦 模糊控制器 仿真

1 引言

电弧炉炼钢是依靠三相电极和炉料之间放电产生的电弧，使电能在弧光中转变为热能，并借助辐射和电弧的直接作用加热并熔化金属和炉渣，冶炼出各种成分的钢和合金的一种冶炼方法。电弧炉三相电极之间存在耦合作用，严重影响了三相电极的控制效果，若不采用解耦措施，某一相电极发生升降，另外两相在电流扰动下，需经过若干次调节才能重新平衡，必然使调节时间增长，能耗变大。针对三相电极之间的耦合关系，毛志忠等人提出了具有前馈环节的电弧炉电极升降自适应控制器，然而前馈项系数难以确定[1]。文献[2]提出基于状态反馈的电弧炉解耦控制器，该控制方法仅在平衡点附近有效，当系统平衡点改变时控制器需重构。文献[3-4]提出了神经网络自适应解耦，但是神经网络存在自学习过程，响应时间较慢。文献[5]提出了三相电流变化与三相弧长变化的矩阵运算关系，但是补偿系数的计算量较大且烦琐。为了解决上述问题，本文在推导出电气部分模型的基础上引入模糊器进行补偿解耦[6-8]，通过设定合适的模糊规则，使三相电极之间的电流影响小到允许范围内。仿真结果验证了引入模糊器可以有效抑制电极间耦合，提高系统的抗干扰性，从而提高电弧炉炼钢效率，降低能耗。

2 电极解耦模型

三相电极的单个电极等效电路如图1所示。

图1 一相电极等效电路Fig.1 The equivalent circuit of a phase electrode

由图1可得电压值Ui为

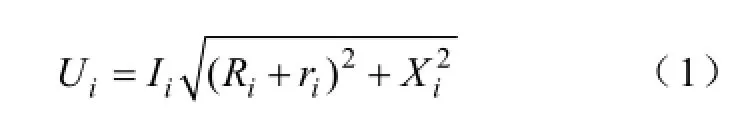
式中，Ri为电路等效电阻；ri为电弧电阻；Xi为电路等效电抗；i=1, 2, 3。

假设变压器二次端到电炉的短网电路上的等效电阻和电感均相等，即R1=R2=R3；X1=X2=X3。

对于交流电弧炉，其电弧电压是很难测得的，在计算弧压时采用Billings理论推导的弧压表达式Uh=α+βLh[9]，其中，а为阴阳两极区电压降和。当电极材料、气体压力和周围介质一定时，通常认为а为常数，单位为V；β为电弧系数，即弧柱的电压梯度，是温度T的函数，单位为V/mm。

三相电极电路如图2所示。Z1、Z2、Z3分别为三相电路的总阻抗，当各相弧长不相等时，此星形电路为三相不对称负载，采取回路电压法和节点电流法列出如下方程组

图2 三相电极耦合电路Fig.2 The coupling circuit of three-phase electrode

可得

式中，Zi=Ri+ri+Xi(i=1,2,3)；Z123=Z1Z2+Z1Z3+Z2Z3。

当r1发生变化时，I1随其产生的变化量为

令

由式（4）得电流增量为

由Billings理论计算式可得

故

同理得

因为无中线的星形电路的三相电弧电流存在耦合，当一相电流受到扰动时，另外两相电流都将变化。当r2、r3不变，r1受到扰动，对另外两相电流引起的变化为

同理可得r2、r3受到扰动引起的电流变化为

根据上述推导可得三相电极调节系统电气部分的模型为

式中，Ki、Mji是电弧电流随弧长变化的自变和互扰系数，自变系数和互扰系数构成弧长与弧流的耦合关系矩阵。事实上，由于电弧炉主电路时间常数远小于电极调节系统的等效时间常数[10-11]，因此可以将电弧炉主电路视为一个静态环节。

3 模糊补偿解耦

传统的解耦方法包括对角矩阵解耦、相对增益法解耦和状态反馈法解耦。这些解耦方法具有原理简单，直观有效的优点，但是应用范围仅适用于线性、定常且有精确的数学模型的理想对象。找出合适的解耦矩阵通常情况下比较困难，需要进行深入分析，反复尝试，计算烦琐，工作量大。

根据式（13）电流之间的耦合关系，进行反馈补偿解耦的方法对三相电极解耦在理论上可行，但是自变系数Ki和互扰系数Mji与扰动发生时刻的电弧电阻ri相关，而电弧电阻ri是由该时刻弧长Li决定的[12]。因此选取不同的静态工作点时，由于弧长Li不同，则对应的Ki、Mji需要重新计算，其计算烦琐，且计算量较大。

电弧炉系统的数学模型是非线性、时变的多变量复杂模型，可以采用智能控制方法进行解耦，故引入单输入双输出的模糊器，根据建立的模糊规则，进行模糊补偿解耦。以弧长Li作为模糊器的输入，根据检测到不同的弧长Li，进行模糊计算，模糊输出值Mji为补偿系数，用以计算补偿电流值。

首先根据Mji随弧长Li变化规律，以及补偿控制的经验，提出一套完整的控制规则；再根据系统当前的运行状态，经过模糊推理、模糊判决等运算，求出控制量，实现对被控对象的控制[13-14]。

输入模糊化:根据补偿系数随弧长的变化规律、将观测量弧长Li的值模糊化为六级:很小（VS）、小（S）、中（M）、大（B）、很大（VB）和太大（TB）。图3为弧长Li的输入隶属函数曲线。

图3 弧长Li输入隶属函数Fig.3 Input membership function of arc length Li

弧长Li的隶属函数选取方法为

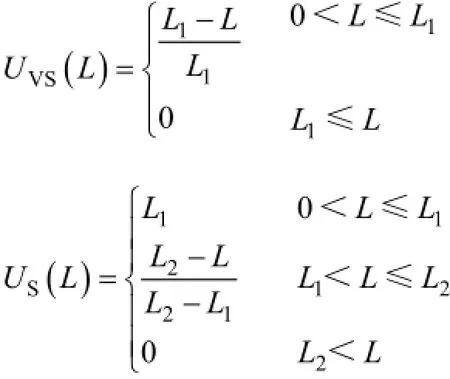
输出模糊化:当U相电弧弧长Li由0变到400mm时，即U相由短路变为断路，U相电弧电流由最大变为零，V和W相电弧电流随U相电弧弧长变化情况如图4所示。

图4 U、V、W三相电流随U相弧长变化曲线Fig.4 Change curves of U, V, W three-phase current with U phase arc length

通过分析图4得到以下结论:某一相短路时，该相弧长扰动对其中一相影响大，对另一相影响较小。如U相主要影响W相，对V相影响较小；V相主要影响U相，W相主要影响V相。某一相断路时，该相弧长扰动对另外两相的影响都很小。当某相弧长由0变到400mm时，该相弧长变化对另外两相电流的影响逐渐变小。

由于某一相电弧长度的变化对另外两相电流的影响不同，因此根据其影响规律制定了不同的模糊输出，以U相弧长扰动为例，V、W相电弧电流受U相扰动影响，只与U相变化前的弧长L和弧长变化量ΔL相关，根据U相变化前的弧长值进行模糊计算，将计算结果与ΔL的乘积作为补偿送到另外两相电流来抵消干扰电流值。

图5和图6为模糊输出MWU、MVU的隶属函数曲线。

图5 输出MWU隶属函数Fig.5 Membership function of output MWU

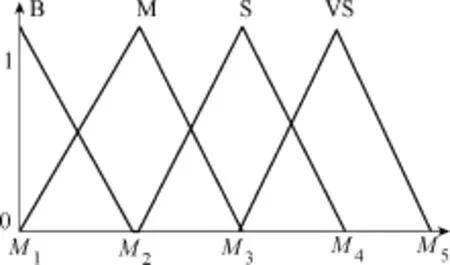
图6 输出MVU隶属函数Fig.6 Membership function of output MVU

根据对象实际情况和操作经验，将模糊规则制定为

If LUis VS，then MVUis B，MWUis VB；

if LUis S，then MVUis B，MWUis B；

if LUis M，then MVUis M，MWUis M；

if LUis B，then MVUis M，MWUis S；

if LUis VB，then MVUis S，MWUis VS；

if LUis TB，then MVUis VS，MWUis TS。

采用Mamdani法表示以上控制规则对应的模糊关系为

由于模糊控制方法属于智能控制技术，可以解决那些用传统控制方法难以解决的复杂系统的控制问题。电弧炉系统的模型复杂，具有高度非线性以及时变性的特点。引入模糊控制器可以适应对象的复杂性和不确定性，因此模糊补偿解耦与传统解耦方法相比较优势明显，主要表现在模糊控制器构造容易，鲁棒性和适应性好，避免建立精确模型，减少计算工作量，使得解耦控制简单高效。

4 控制器解耦及干扰抑制

4.1三相电极电流解耦

为验证模糊器补偿解耦性能，需要分别对其解耦性，抗干扰性进行仿真。根据电弧电流补偿解耦原理[15-16]，设计的电弧炉电极调节系统如图7所示。

引入模糊器进行补偿解耦后，U、V、W三相电流随U相弧长变化情况如图8所示。其中U、V、W表示补偿前电流，U1、V1、W1表示模糊补偿后电流。

仿真结果表明:补偿后在U相弧长由0变化至400mm时，只有U相电路电流从短路到断路变化显著，V、W两相电流在模糊器补偿下受U相电弧长度变化影响都很小，达到允许误差范围内。

图7 模糊解耦电极调节系统Fig.7 Electrode regulating system of fuzzy decoupling

图8 模糊补偿前后三相电流随U相弧长变化曲线Fig.8 Change curves of three-phase current with U phase arc length between pre and post fuzzy compensating

为进一步验证控制器的解耦性能，对电弧炉炼钢生产过程采集了20组数据进行验证。图9和图10为解耦前后三相电流实测值的变化曲线。通过仿真结果的前后对比，可以明显看出解耦之后的三相电流变化减小，稳定性提高，达到模糊器补偿解耦的效果，解耦性良好。

图9 解耦之前的三相电流实测曲线Fig.9 Curves of three-phase current measured values before Decoupling

图10 解耦之后的三相电流实测曲线Fig.10 Curves of three-phase current measured values after Decoupling

4.2模糊控制器抗干扰性

电弧炉三相电弧长度在100mm处三相电流处于平衡状态，平稳运行5s后，U相电弧弧长受到扰动，由100mm变为200mm时，U、V、W三相电流在进行模糊补偿解耦前后随U相弧长扰动影响情况如图11和图12所示。

图11 模糊解耦前三相电流在弧长扰动下的曲线Fig.11 Curve of three-phase current in the condition of the arc length disturbance before fuzzy decoupling

图12 模糊解耦后三相电流在弧长扰动下曲线Fig.12 Curve of three-phase current in the condition of the arc length disturbance after fuzzy decoupling

仿真结果表明引入模糊器进行补偿解耦后，某一相电弧弧长受到扰动，另外两相电弧电流在解耦器的补偿下，能减弱甚至抵消弧长扰动对这两相电弧电流的影响，使电极调节系统真正地实现对某一相的单独控制。模糊补偿解耦器能够大大削弱一相弧长扰动对两外两相电流的影响，抗干扰性良好。

5 结论

电弧炉三相电极之间存在耦合作用，严重影响了对三相电极的控制效果。本文在电流补偿解耦的基础上引入模糊控制器，解决了互扰补偿系数复杂且难以计算的问题，该系统解耦性、抗干扰性均达到了满意的结果。因此，带模糊补偿解耦的电弧炉电极调节系统，解耦效果明显，调节时间缩短，可实现对某相电极的独立控制。

[1] 毛志忠, 李健. 具有前馈环节的电弧炉电极升降自适应控制器[J]. 东北大学学报(自然科学版), 1996, 17(1)： 65-68.

Mao Zhizhong, Li Jian. Adaptive controller of an electric arc furnace with feedforward[J]. Journal of Northeastern University (Natural Science), 1996, 17(1)： 65-68.

[2] Anna S H, Arnar G, Ariv V. Current control of a three-phase submerged arc ferrosilicon furnace[J]. Control Engineering Practice, 2002, 10 (4)： 457-463.

[3] 赵辉, 吴晓辰, 王红君, 等. 电弧炉电极调节器的优化仿真[J]. 计算机仿真, 2012, 29(5)： 192-195.

Zhao Hui, Wu Xiaochen, Wang Hongjun, et al. Electrode adjustment of electric arc furnace based on DRNN neural network PID controller[J]. Journal of Computer Simulation, 2012, 29(5)： 192-195.

[4] Shu Huailin, Pi Youguo. Decoupled temperature control system based on PID neural network[C]. ACESE05 Conference, Cairo： Acse, 2005： 19-28.

[5] 池世春. 模糊PID算法在电弧炉电极控制中的研究[D]. 沈阳： 东北大学, 2005.

[6] 骆玲玲. 电弧炉电极调节系统的智能解耦控制[D].沈阳： 东北大学, 2009.

[7] Wang L X. Stable adaptive fuzzy control of nonlinear systems[J]. IEEE Transaction on Fuzzy Systems, 1993, 1 (2)： 146-155.

[8] 张绍德, 毛雪菲, 毛雪芹. 基于最近邻聚类支持向量机辨识的电弧炉电极逆控制[J]. 控制理论与应用, 2010, 27(7)： 909-915.

Zhang Shaode, Mao Xuefei, Mao Xueqin. Inverse control for electrodes in electric arc furnace based on support-vector-machines identification on nearest neighbor clustering[J]. Journal of Control Theory and Applications, 2010, 27(7)： 909-915.

[9] 李媛, 王建, 王艳秋. 三相电极调节器的建模及其仿真研究[J]. 电工技术学报, 1999, 14(1)： 23-26.

Li Yuan, Wang Jian, Wang Yanqiu. Mathematical modelling of the three-phase electrode regulator and simulation[J]. Journal of Transactions of China Electrotechnical Society, 1999, 14(1)： 23-26.

[10] 李磊, 毛志忠. 基于近似模型的电弧炉解耦控制器[J]. 控制理论与应用, 2013, 30(1)： 101-110.

Li Lei, Mao Zhizhong. Approximate model based decoupling controller for electric arc furnace[J]. Journal of Control Theory and Applications, 2013, 30(1)： 101-110.

[11] 李强, 潘永湘, 余健明, 等. 综合智能控制策略在电弧炉控制中的应用[J]. 电工技术学报, 2003, 18(1)： 100-104.

Li Qiang, Pan Yongxiang, Yu Jiang, et al. Application of genetic neural control strategies in high-impedance electric arc furnace[J]. Transactions of China Electrotechnical Society, 2003, 18(1)： 100-104.

[12] 王琰, 毛志忠, 田慧欣, 等. 基于自适应变异差分进化算法的电弧时域模型[J]. 仪器仪表学报, 2009, 30(3)： 554-558.

Wang Yan, Mao Zhizhong, Tian Huixin, et al. Time domain electric arc model based on ADE[J]. Chinese Journal of Scientific Instrument, 2009, 30(3)： 554-558.

[13] 蒯熔, 刘小河. 电弧炉电极调节系统的模糊-PID控制研究[J]. 机床与液压, 2008, 36(7)： 270-272.

Kuai Rong, Liu Xiaohe. Research on fuzzy PID control for electric furnace[J]. Journal of Machine Tool and Hydraulics, 2008, 36(7)： 270-272.

[14] 增光奇, 胡均安, 王东, 等. 模糊控制理论与工程应用[M]. 武汉： 华中科技大学出版社, 2006.

[15] Mokhtari H, Hejri M. A new three phase time- domain model for electric arc furnaces using Matlab[C]. Transmission and Distribution Conference and Exhibition, 2002, vol. 3： 2078-2083.

[16] 石新春, 付超, 马巍巍, 等. 基于实测数据的电弧炉实时数字仿真模型及其实现[J]. 电工技术学报, 2009, 24(7)： 177-182.

Shi Xinchun, Fu Chao, Ma Weiwei, et al. A real-time digital simulation model and its implementation for arc furnace based on recorded field data[J]. Transactions of China Electrotechnical Society, 2009, 24(7)：177-182.

The control effect of three-phase electrode is severely affected by the coupling between three electrode of electric arc furnace, and the large maladjustment is easy to occur in ordinary single-phase control method without considering the coupling. On the basis of analyzing the threephase electrode coupled, a decoupling method on current compensation is derived in this paper. The method has theoretical significance for electrode decoupling, but the compensation coefficient is associated with the arc length on time and the computational complexity is very great. Therefore, a fuzzy controller of single-input and double-output, which is used to compensate and decouple, is introduced based on decoupling method of the current compensation. Simulation is made on decoupling performance and noise immunity of the controller by Matlab/Simulink and the comparison has been made before and after decoupling by the collected data on field. The results show that the fuzzy decoupling controller can eliminate the strong coupling effect between the three-phase electrodes, and improve the efficiency and reduce energy consumption of electric arc furnace steelmaking.

Electric arc furnace, three-phase coupling, decoupling, fuzzy controller, simulation

TP273

鲁 军 男，1965年生，博士，副教授，研究方向为智能材料及智能控制系统。

国家自然科学基金（51377110），辽宁省自然科学基金（201102184）和沈阳市科技计划（F12-277-1-28）资助项目。

2014-11-20 改稿日期 2015-04-05

Fuzzy Decoupling Controller on Electrode Regulator System of Electric Arc Furnace

Lu Jun1 Huo Jinbiao1 Zhang Guangyue2

（1. Shenyang Ligong University Shenyang 110159 China 2. Tianjin Design & Research on Electric drive Co, Ltd Tianjin 300180 China）

霍金彪 男，1990年生，硕士研究生，研究方向为控制理论与控制工程。