关于高中数学解题技巧的应用

张春华

（江苏省包场高级中学）

高中数学理论是化归思想的体现，学生通过观察数学问题的题根，理解问题，抓住数学问题的题眼，有效地转化问题，顺藤摸瓜地梳理题目的经络，融合所学到的一系列基础知识和技能，灵活运用并展开数学解题技巧，将数学问题化繁为简，化整为零，建立起自己的数学解题王国。关于高中数学解题技巧有如下几种：

一、“构造法+函数法”的结合

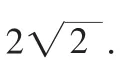
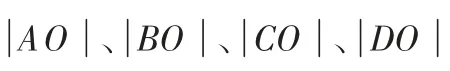
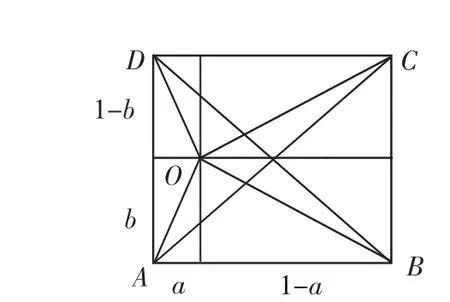
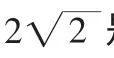
而且本题还可以从另一个思路进行解答，就是运用复数模的概念，将相联系的数据和看成一个模函数，仍然可以得到所求的结果。

二、转换法

这种方法是体现学生的想象力及创新能力的方法，也是数学解题技巧中最富有挑战性的方法，能将复杂的题型辅以转换的功能，成为简单的、易被理解的题型。比如，一个正方体平面为ABCB和A1B1C1D1，在正方体的棱长D1C1和C1B1分别设置两点E 和F 为中点，AC 与BD 相交于P 点，A1C1于EF 相交于Q 点，求证：（1）点D、B、F、B 在同一平面上；（2）如果线段A1C 通过平面DBFE，交点到R 点，那么P、R、Q 三点共线？

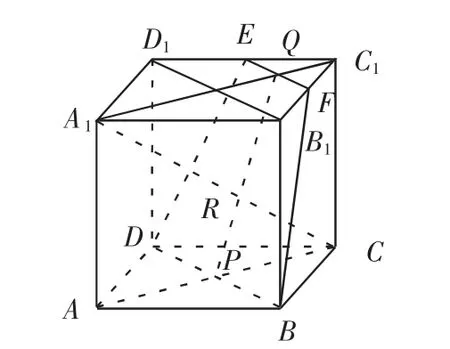
解题（1）：由题可知：线段EF 是△D1B1C1的中位线，所以，EF与B1D1平行，在正方体AC1中，线段B1D1与BD 平行，相应得出：线段EF 与线段BD 相平行，由此得出线段EF 和BD 在一个平面，所以可以求得点D、B、F、E 在同一个平面。

解题（2）：假设平面A1ACC1为x，平面BDEF 为y，由于Q 点在平面AC，所以Q 点也属于平面x，为x 和y 的交点，同属两个平面的点。同理可得，点P 也属x、y 的公共点，而R 点是平面A1C 与平面y 的交点，所以，可以得到P、Q、R 三点共线。

三、反证法

任何事物的结果有时顺着程序去思考，往往不得要领，倘若从结果向事物开始的方向或用假设的反方向去推理，反倒会“一片洞天”。数学解题技巧也是如此。首先，假设命题结论相反的答案，顺理演绎地解答，得出假设的矛盾结果，从另一侧面论证了正确答案。例如，苏教版教材必修1《函数》章节，已知函数f（x）是一项正负无限大范围内的增函数，a、b 都为实数，求证：（1）假设：（a+b）≥0，则函数式表示为：f（a）+f（b）≥f（-a）+f（-b）成立；（2）求证（1）问中逆命题是否正确。

解题分析：（1）因为（a+b）≥0，移项后，可得：a≥-b，由于函数为单调递增函数，则：f（a）≥f（-b），又（a+b）≥0，移项后，可得：b≥-a，f（b）≥f（-a）；两个方程相加，得：f（a）+f（b）≥f（-a）+f（-b），由此证明完毕。

解题（2）分析思路就是由（1）中得出的结论f（a）+f（b）≥f（-a）+f（-b），反证得出（a+b）≥0 是否成立。于是，我们先假设（a+b）＜0成立，那么，移项后，分别出现两个不等式函数，即：f（a）＜f（-b）；f（b）＜f（-a），两个方程组合后，得到：f（a）+f（b）≤f（-a）+f（-b），显然与先决条件不符，所以，可以得出只有（a+b）≥0，方可得到正确的答案。逆命题得证。

四、逐项消除法（也可称：归纳法）

这种方法就是将数列前项与后项进行规律查找，逐项消除或归纳合并的方法去求得答案。在苏教版必修5《数列》章节中，有一道习题为：求：1/2+2/3！+3/4！+4/5！+5/6！+…+（n-1）/n！的和；

解题分析：这道习题就是按照一定的规律进行递增的集合，那么，就可以运用求和的公式，转化为：Sn=1/1-1/2+1/2+1/3+…+1/（n-2）！-1/（n-1）！+1/（n-1）！-1/n=1-（1/n）的形式进行解答，使解题的速度效率提高。

数学解题方法多种多样，熟练掌握解题技巧不但可以发掘出学生的创新思维，而且可以通过发散性思维激发起学生的学习兴趣，将数学成为万变的花筒，神奇又有趣，更好地培养高中生善于思考，细心观察，不断总结的良好习惯。既锻炼了高中生的逻辑思维能力，又练就了他们多角度、多层次地分析问题、解决问题的能力。

［1］杨金慧.论数学中的化归思想［J］.考试周刊，2013（78）.

［2］邱小兰.高中数学教学中解题策略的探究［J］.理科考试研究，2014（09）.