例谈简单分式型正、余切三角函数最值（值域）的求法

邱芳忠

（江西省信丰县第七中学）

函数最值和值域的求法是高中数学函数的一个重点，也是难点，更是每年高考的热点.而三角函数最值和值域的求法比一般函数最值和值域的求法，其解题过程要更复杂，解题方法要更灵活，解题技巧要更多样.本文就以简单分式型正、余切三角函数为例，对其最值和值域的求法加以归类并指出解题方法.

解法1：（“1”的代换与公式法的结合）

所以原函数的值域为y∈｛y|y≠1｝.

点评：上面的解题过程，要注意“1”代换的内容和两角和与差正切公式的正确运用。

解法2：（分离常数法）

从而原函数的值域为y∈｛y|y≠1｝.

点评：当分式型三角函数的分子和分母都一次式时，首先应对其进行常数分离，这样问题就自然迎刃而解了.

解法1：（多次换元与二次函数配方的结合）

因为Δ=22-4×1×2=-4＜0，所以u（t）＞0，从而y＞0.

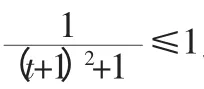
综上所述，原函数的值域为y∈（0，2］.

点评：有些数学问题利用多次换元后，复杂的式子就变得简单多了，要求解的问题立刻跃然纸上，这感觉犹如“山重水复疑无路，柳暗花明又一村”.

解法2：（判别式法）

原函数可变为：ytan2x+2ytanx+2y-2=0（tanx∈R），

当y=0 时，-2=0 显然不成立，所以y≠0；

从而由△≥0 可得到：4y2-4y（2y-2）≥0，即y2-2y≤0，解得0≤y≤2.

因为y≠0，所以0＜y≤2，从而得到原函数的值域为y∈（0，2］.

点评：运用判别式法求分式型三角函数的值域时，首先要保证自变量取自身的范围；其次去分母变形后所得到二次方程，要讨论二次项系数为零与不为零的情况.

解：（等价转化与换元、二次函数配方的结合）

点评：当所给的简单分式型三角函数是齐次式的正、余弦函数时，习惯上把它转化成分式型正切函数来求解问题.