混合粒子群算法用于共沸精馏塔的最优设计

李红海，姜　奕，陶少辉

(青岛科技大学化工学院，山东青岛266042)

美国的一项统计数据表明［1］，化工过程中有40%～50%的能耗用于分离，而这其中又有95%的能耗在精馏过程中，因此精馏塔的最优设计问题的研究方兴未艾［2－3］。

精馏塔设计是一个在给定分离要求下确定分离所需塔板数、进料位置和回流比，进而确定塔高塔径等的设计过程。最优设计与一般设计相比，需要在能够完成分离要求的基础上，权衡能耗费用与投资费用，最终使年度总费用(Total Annual Cost，TAC)最低。由于塔板数、进料位置为整数变量，而回流比为连续变量，且精馏过程具有强非线性，因此精馏塔的最优设计是一个混合整数非线性规划(Mixedintegernonlinearprogramming，MINLP)问题［4］。

为使优化结果具有实际应用价值，在优化时应考虑空塔气速处于合适的范围内等实际问题，而目前涉及这一点的参考文献并不多［5］。本研究建立了包含流体力学约束的精馏塔最优设计模型，提出了适于求解该问题的混合粒子群优化(Mixed particle swarm optimization，MPSO)算法，并将之用于一个醋酸甲酯/甲醇/水三元共沸精馏塔的最优设计问题计算。

1　MINLP求解的混合粒子群优化算法

1.1　混合整数非线性规划简介

混合整数非线性规划(Mixed integer nonlinear programming，MINLP)问题的数学模型如下:

式(1)中，x为n维实数向量，y为m维整数向量，f(x，y)与gi(x，y)分别为目标函数与约束函数。

MINLP求解常用的确定性算法有分支界定法［6］、外部逼近法［7］和广义 Benders 分解法［8］等。这些确定性算法具有能够找到精确的最优局部解的优点，但随着问题规模的扩大，确定性算法所需的求解时间大幅度增加，并且不能保证得到任意非凸问题的全局最优解，因此，研究启发式算法对于MINLP问题的求解有着实际意义［9］。可改造并用于MINLP问题求解的启发式算法有遗传算法［10］(Genetic Algorithm，GA)，粒子群算法［11］(Particle swarmoptimization， PSO)，模拟退火算法［12］(Simulated Annealing，SA)，蚁群算法［13］(Ant Colony Optimization，ACO)等。

1.2　粒子群算法(PSO)简介

粒子群优化算法迭代公式为:

(2)和(3)式中，vi，t代表第 i个粒子在第 t次迭代中的速度，xi，t代表第i个粒子在第t次迭代中的位置，c1，c2分别为认知学习因子和社会学习因子，用于模拟自身经验与社会经验在种群中的影响，rand 为(0，1)范围内的随机数值，pi，t与 pg，t分别是每个粒子在第t次迭代中的的历史最优位置和所有粒子的全局最优位置。ω代表惯性权重(通常为0.8左右)，随着迭代的进行，ω逐渐减小，这代表随着时间推移，新迭代出的粒子的速度更多地受历史最优的影响，自身之前的速度对其影响逐渐降低。

相比于其它启发式算法，PSO在形式上相对简单且效率较高，因此在化工领域中获得了广泛的应用［14］。

1.3　混合粒子群算法

本文选用了易实现且效率较高的PSO优化算法，并针对精馏过程模拟这一MINLP问题，将之改造为混合粒子群算法(MPSO)。在该算法中，本研究以回流比R和精馏段板数NR与提馏段板数NS作为待优化变量，优化过程中对塔板数采用贺益君等［15］提出的整数处理方法;产品纯度与流体力学要求则采用Deb［16］处理方法。该算法流程如图1所示。

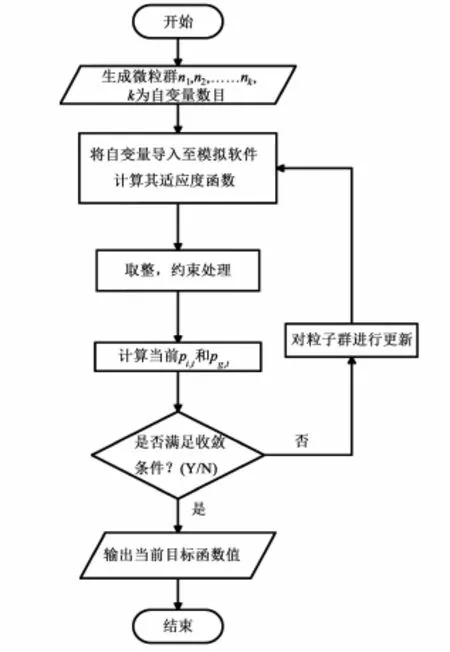
图1MPSO算法流程图Fig．1　The flow chart of MPSO algorithm

本研究中算法的收敛条件取为:

式(4)中ft为第t次迭代后最优粒子所对应的目标函数值，ε为常数，通过对ε的调整可调整收敛精度。

2　共沸精馏塔的最优设计

精馏塔设备投资的费用，在概念设计阶段通常只以理论板数的考虑为主。对于操作费用而言，进料量、回流比、进料位置和操作压力等是影响其能耗，进而影响其操作费用的重要参数。但由于在实际的工业工程中，物料的进料量绝大多数时候是由上游给定的，操作压力也需要综合整个系统来考虑，这两者并不总是具有很大的操作弹性。

在以往的研究当中，精馏塔的流体力学约束常常被忽略，而流体力学约束其实是设计和优化过程中的重要因素，如若不符合该约束，则优化结果无法应用于实际。对于板式塔，其各塔板上气液两相的流体力学状况需要其流体力学性能图中各V-L关系曲线所围成的适宜气、液流量范围内，而填料塔的空塔气速和液体喷淋密度也必须在合理的范围内，这一点目前的参考文献则考虑较少［17］。为使得优化结果更具实际意义，本文建立了考虑流体力学约束的精馏塔最优设计数学模型。

在优化过程中，以C++编写MPSO算法，即粒子的初始化、位置移动和收敛判断变量适应度函数;以ASPEN模型进行粒子适应度和塔径的初步计算;以C#为平台，将粒子位置(塔的待优化参数)导入ASPEN，获取计算TAC和约束函数值所需的参数值。如此则可充分应用ASPEN的功能，降低复杂设备精馏塔优化设计的难度。

2.1　最优设计数学模型

将MPSO应用于共沸精馏塔的最优设计，即以回流比R和精馏段板数NR，提馏段板数NS作为待优化变量，目标函数为最终的年度总费用TAC最小。TAC的计算数学模型如下:

式(5)中，Cco，Cex，Cen分别指塔器成本，冷凝器与再沸器成本和年度能耗费用，是塔径、进料流量以及分离条件的函数，INV为投资回收期(年)，该式标表明了TAC是设备投资费用与能耗费用的函数，其具体的计算过程见文献［18］。式(6)中，xD与xW分别为塔顶与塔底关键组分的摩尔百分数(该式中分别以塔顶重关键组分与塔底轻关键组分为例)，xHD(摩尔分数，下同)与xLW则为对应的塔顶塔底的目标浓度要求，由ASPEN直接导出;ui代表第i块板上的空塔气速(m/s)，σ代表液体喷淋密度［m3/(m2·h)］，二者都是塔径和进料流量以及热负荷的函数，分别根据ASPEN导出的各板上的气液相流量由C#进行计算。

2.2　共沸精馏最优设计的约束处理2.2.1　产品纯度约束

产品的纯度要求根据实际情况，主要考虑塔顶产品要求与塔底产品要求。设指标为塔顶组分浓度要求xHD，塔底浓度要求为xLW，则塔顶产品纯度约束方法为:

同理，塔底的产品纯度约束方法为

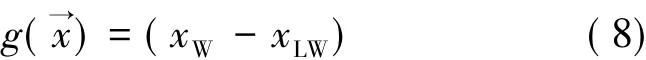
2.2.2流体力学约束

Aspen Plus中具有流体力学计算功能，能够根据所建立的模型计算出每一块理论板上的气液相流量，进而根据塔径计算出每一块理论板上的空塔气速与液体喷淋密度。

对于填料塔，当其每一级理论板上的空塔气速ui范围在［0.5，2.0］，喷淋密度 σmin＞0.5时，该模拟结果满足流体力学约束。喷淋密度由回流比决定，而回流比越大则能耗越高，操作费用也随之增加，导致优化过程中回流比总是趋于最小值，因此需要设定喷淋密度下限。ui与σmin均根据工程经验得出［19］。如不满足，则令

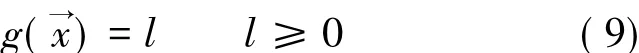
因为流体力学校核只存在满足与不满足两种情况，所以式中的l为一个常数。

2.3　模拟的建立与运行

以醋酸甲酯/甲醇/水三元共沸体系为例［18］，该体系中，水与醋酸甲酯，甲醇与醋酸甲酯分别共沸。塔顶蒸出醇酯共沸物，塔底分离出水和醇。根据案例要求，需要塔顶共沸物含量尽可能高。

工程模拟采用文献［18］数据。精馏塔为Mellpak750Y型规整填料的不锈钢填料塔，冷凝器与再沸器的传热系数分别为0.568和0.852 kW/(K·m2)，对数平均温差为13.9和34.8 K，能耗成本为0.3/GJ与4.7/GJ。流体采用常压下泡点进料，其中进料组成(物质的量)为20%水，50%甲醇，30%乙酸甲酯，要求塔顶水含量≤0.1%，塔底酯含量≤0.1%，进料量 0.1000 kmol/s，塔顶采出量 0.0443 kmol/s。

表1　MPSO算法相关参数Table 1　Related Parameters of MPSO Algorithm

表1中为MPSO算法的相关参数，均为自设，回流比位置上下限，步长范围均经过多次调整最后得出。其中精馏段理论板数的步长不为整数，而是在每次迭代后取整，这样，对于粒子群算法中精馏段板数这一变量的寻优步长，若更新至最大步长vmax或最小步长－vmax，则在取整时会有相同的概率取到步长前后的整数，使粒子位置的更新存在更大的灵活性。粒子个数取28，最大迭代次数取50次，收敛精度为控制算法收敛的变量，该参数为1×10－3。

经过编写程序进行运算，得出的最优结果如表2所示，其中第二行中的数据为文献［18］中计算的数据。总理论板数NT与进料位置NF由精馏段板数NR与提馏段板数NS计算得出。Di为圆整后的塔径，流体力学约束在该塔径下校核，经过计算最终得出的结果符合所有约束。

表2　模拟计算数据记录Table 2　The Simulation data records

可见，本研究计算的 R，NT，NF分别为 0.94，34和27，塔径为 1.9 m，TAC的最优结果为 7.14×105美元/a。而文献［18］通过灵敏度分析法得出回流比为1.96，是MPSO法计算值的2倍;且理论板数与塔径均比MPSO法小得多。这说明灵敏度分析法预测的塔内气液相负荷远大于MPSO法的预测结果。灵敏度分析法的TAC的最优结果为7.14×105美元/a。但使用本文所述的方法校核后发现其在填料塔中的TAC高达9.27×105美元/a，且本研究校核后发现Di=1.38 m的塔径令空塔气速ui＜0.5，故无法满足流体力学约束。若要使其满足，则需将塔径增加至2.4 m，最终满足实际生产要求的TAC达到9.95×105美元/a。这说明本研究的MPSO法的计算结果明显优于文献结果，且具有实用价值。

3　结论

1)将PSO结合的MINLP应用于共沸精馏塔的最优设计中，计算结果表明该方法能够应用于工业设计与优化，并且计算结果优于文献数据。

2)将流体力学约束考虑到算法当中，相比于之前的设计模拟，得出的结果更具有实际意义。

参考文献:

［1］李英劼．化工生产中降低精馏技术能耗的思路［J］．石油与化工设备，2011，14:58－60 Li Yinghai．Thinking to reduce the energy consumption of distillation in chemical production［J］．Petro ＆ Chemical Equipment，2011，14:58－60(in Chinese)

［2］吴晓艺，王静文，司秀丽．拉格朗日插值算法在图解法精馏塔设计中的应用［J］．计算机与应用化学，2009，26(3):311－314 Wu Xiaoyi，Wang Jingwen，Si Xiuli．The application of Lagrange’s interpolation applied to the design rectifying tower with graphic method［J］．Computers and Applied Chemistry，2009，26(3):311－314(in Chinese)

［3］李俊妮，栗秀萍，刘有智，等．分段抛物插值算法在精馏塔设计中的应用研究［J］．计算机与应用化学，2012，29(5):611－614 Li Junni，Li Xiuping，Liu Youzhi，et al．The research of subsection parabolic interpolation applied to the design of rectifying column［J］．Computers and Applied Chemistry，2012，29(5):611－614(in Chinese)

［4］Jagadisan．V，Ignacio G．Optimal Feed locations and number of trays for distillation columns with multiple feeds［J］．Industrial＆EngineeringChemistry Research，1993，32，2 942－2 949

［5］王晓玲，刘春江，余国琮．计算流体力学在精馏塔板上的应用［J］．化学工业与工程，2001，18(6):390－394 WangXiaoling， LiuChunjiang， YuGuozong．Application of computional fluid dynamics on distillation tray［J］．Chemical Industry and Engineering，2001，18(6):390－394(in Chinese)

［6］Borchers B，Mitchell J E．An improved branch and boundalgorithmformixed-integernonlinear programming［J］．Computers and Operations Research，1994，21(4):359－367

［7］DuranA， GrossmannE． Anouter-approximation algorithm for a class of mixed-integer nonlinear programs［J］．Mathematical Programming，1986，36(3):307－339

［8］Zhu Y，Takahito K．Global optimization of non-convex MINLP by a hybrid branch-and-bound and revised general benders decomposition approach［J］．Industrial＆ Engineering Chemistry Research，2003，42(3):528－539

［9］Burer S，Letchford N．Non-Convex mixed-integer nonlinear programming:A survey［J］．Surveys in Operations Research and Management Science，2012:97－106

［10］BerndG， PeterR．Totalprocessoptimizationin chemical engineering with evolutionary algorithms［J］．Computers ＆ Chemical Engineering，1998，22:229－236

［11］薛峰，陈刚，高尚．求解0—1规划的混合粒子群优化算法［J］．计算机技术与自动化，2011，30(1):86－89 Xue Feng， Chen Gang， Gao Shang．Solving 0—1 integer programming problem by hybird particle swarm optimization algorithm ［J］．Computing Technology and Automation，2011，30(1):86－89(in Chinese)

［12］宋燕子．基于模拟退火算法的启发式算法在VRP中的应用［D］．武汉:华中师范大学，2013 Song Yanzi．Theapplication of heuristic algorithm in VRP based on the simulated annealing algorithm［D］．Wuhan:Huazhong Normal University，2013(in Chinese)

［13］杨剑锋．蚁群算法及其应用研究［D］．杭州:浙江大学，2007 Yang Jianfeng．Research on ant colony algorithm and application［D］．Hangzhou:Zhejiang University，2007(in Chinese)

［14］任再敏，高岳林，李济民，等．非线性整数规划问题的改进粒子群优化算法［J］．武汉理工大学学报:交通科学工程版，2012，36(6):1 296－1 300 Ren Zaimin，Gao Yuelin，Li Jimin，et al．Improved particle swarm optimization algorithm for nonlinear integer programming problems［J］．Journal of Wuhan University of Technology:Transportation Science ＆ Engineering，2012，36(6):1 296－1 300(in Chinese)

［15］贺益君，陈德钊．适于混合整数非线性规划的混合粒子群优化算法［J］．浙江大学学报:工学版，2008，42(5):747－751 He Yijun，Chen Dezhao．Hybrid particle swarm optimization algorithm for mixed-integer nonlinear programming［J］．JournalofZhejiangUniversity:Engineering Science，2008，42(5):747－751(in Chinese)

［16］Deb K．An efficient constraint handling method for genetic algorithms［J］．Computer Methods in Applied Mechanics and Engineering，2000，186:311－338

［17］Javaloyes J，Ruiz R，Caballero A．Rigorous design of complex distillation columns using process simulators and the particle swarm optimization algorithm ［J］．Industrial＆ Engineering Chemistry Research，2013，52:15 621－15 634

［18］William L．Distillation design and control using aspen simulation［M］．Wiley-AIChE，2006

［19］James M．Perry’s chemical engineers’handbook［M］．McGraw-Hill，2008