Feistel-SP结构迭代差分的自动化搜索*
李艳俊,方 波,2,毛 明,2
(1.西安电子科技大学通信工程学院,陕西 西安 710071;2.北京电子科技学院,北京 100070)
Feistel-SP结构迭代差分的自动化搜索*
李艳俊1,方 波1,2,毛 明1,2
(1.西安电子科技大学通信工程学院,陕西 西安 710071;2.北京电子科技学院,北京 100070)
基于新的符号差分表示方法提出了一种自动化搜索技术,可以搜索出典型Feistel-SP结构的分组密码的最优迭代差分模式,选择合适的迭代差分模式可以遍历出所有最优的迭代差分路径,不仅大大降低计算复杂性,还能通过迭代差分模式构造出多轮最优差分路径。以轻量级分组密码MIBS为例,应用自动化搜索工具,给出了MIBS的3轮、4轮最优迭代差分路径,概率分别为2-20、2-26,并搜索出所有满足条件的最优迭代差分路径。
Feistel-SP;MIBS;自动化搜索;符号差分;迭代差分
1 引言
Feistel网络结构[1]是由Feistel H设计的,它是设计分组密码的典型结构,其优点是加密和解密过程相同或者相似,使得加密和解密速度快,非常有利于软件实现和硬件实现。SP[2]网络结构是除了Feistel网络结构之外的另一种典型结构,SARER、SHARK等著名密码算法都采用此结构。在此结构的每一轮的轮输入首先作用于一个由子密钥控制的可逆函数S(非线性变换),然后再作用于一个置换P(或一个可逆的线性变换)。S一般被称为混淆层,主要起混淆作用,P一般被称为扩散层,主要起扩散作用。很多著名的分组密码算法都是基于这两种结构设计的,Feisetl-SP结构是指将Feistel、SP相结合而形成的一种混合结构,典型密码算法有MIBS[3], E2[4]和Camellia[5]等。
2009年,文献[3]提出一种新的分组密码算法MIBS,整体采用Feistel结构,轮函数为SP结构,以4 bit为一个单位输入,它的分组长度为64 bit,密钥长度为64 bit和80 bit两个版本,轮数为32轮,可以应用到资源受限的微型计算设备上。由于密钥生成对差分分析没有影响,我们只需要考虑算法的差分特征。本文提出了一种新的符号差分表示方法,基于这种符号表示方法进而给出了一种自动化搜索技术,使用自动化搜索工具,我们搜索出3、4轮的最优迭代差分概率,并给出了多条迭代差分路径。第2节介绍了MIBS分组密码算法组成和性质,第3节介绍了差分传播系统,重点说明了差分基本性质和新的差分表示法,第4节给出了3、4轮的自动化搜索算法,第5节对本文工作进行了总结。
2 MIBS分组密码
MIBS整体结构是Feistel结构,轮函数是SPN(Secret Private Network)型,该算法是以4 bit为单位(半字节),由密钥加、S盒替换、M置换和变换层T组成。为了方便描述,我们把线性变换M和T统称为P置换,MIBS的轮函数的具体表达式为:
F[K]=P′S′σ[K]
其中,σ[K]是密钥异或运算。
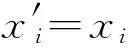
其具体结构如图1所示。
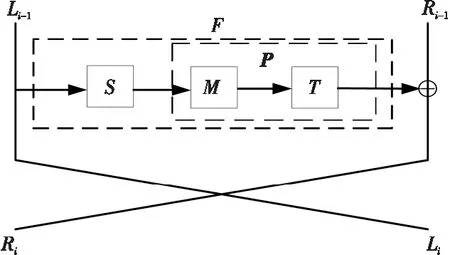
Figure 1 Structure of round function
MIBS的字节替代是由8个相同的S盒组成,S盒是4×4规模大小,每个S盒的最大差分概率是2-2:
F轮函数的线性变换由M置换层、T变换层组成、M置换层表达式如下:
T变换表映射如表1所示。
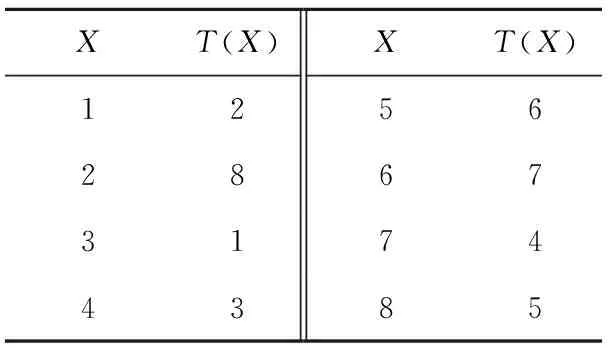
Table 1 T transformation
M-T组成的P矩阵及其逆矩阵可以写成为:

3 差分传播系统
3.1 预备知识
为了更好地研究MIBS迭代差分模式,首先我们对差分传播模式进行说明,引进如下表示方法:ΔXA、ΔYA分别表示A轮的输入差分和输出差分,ΔZA、ΔVZA分别表示A轮S盒的输出差分和P逆置换的输出差分,他们之间的关系为ΔZA=S(ΔXA),ΔYA=P(ΔZA)。这里,ΔX=(Δ1,…,Δx2),Δx1表示第i个S盒的差分。
定义1 轮函数F的一对输入(x,x′),若该输入对导致某个S盒的输入差分非零,则称输入对(输入差分)导致该S盒活跃,或者称S盒针对输入对(输入差分)是活跃的,简称该S盒是差分活跃S盒。
上述定义说明输入差分非0,输出差分非0;输入差分为0,输出差分为0。
定义2[6]SPN轮函数中,差分分支数定义如下:
其中,P是扩散层,△X是输入差分。
定义3[6]若一条i轮差分特征ω=(β0,β1,…,βi)满足β0=βi,这称ω是一条i轮迭代差分特征,若ω是迭代差分特征,则它自身可进行级联。
定义4[7]如果特征满足如下条件:
([Φ],[I]),ΔYm,…,ΔYm′,([J],[Φ])
且中间不包含交换特征,其中[Φ]表示全0比特,[I]和[J]为任意差分,称为m′-m+1轮迭代差分特征。
定义5[7]n轮迭代差分中概率p最大的特征称为最优差分特征,如果它是k轮导出的,称n轮差分特征的最优迭代差分特征为k轮。同样k轮迭代特征中概率p最大的迭代差分特征称为k轮最优迭代差分特征。
定义6 符号差分以Sign表示,如果输入为0,经过符号差分输出为0,如果输入不为0,经过符号差分输出为1。
如Sign(X1,…,Xn)=(A1,…,An),当Xi为0时,Ai为0,当Xi不为0时,Ai为1。
定理1[8]轮函数是SPN型的Feistel结构密码没有两轮迭代差分特征。
上述定理说明Feistel-SP没有两轮迭代差分特征,本文搜索了3、4轮的迭代差分特征。
3.2 差分模式表示法
经过观察,第i-1轮的输出差分对是第i轮的输入差分对,要使第i轮输入的活跃S盒个数最少,考虑P置换的性质可以推测到输入的非零差分之间存在着一定的等价关系。基于这种思想我们采用具有内部关系的符号差分来表示具体的输入差分值,这种表示方式改进了以往的符号差分表示方法[7](输入差分不为零时用1表示,输出差分为零时用0表示)。使用这种具有一定内部关系的迭代差分模式去搜索迭代差分特征,可以大大降低计算复杂性。
本文提出了如下具有差分内部关系的符号差分来搜索多轮最优的迭代差分模式。当输入活跃S盒个数为1、2、3时,内部关系比较简单。主要对输入为4个活跃S盒的情况进行说明,如表2所示,例如:当有4个活跃S盒时,考虑它们内部经过线性变换后的关系,我们定义1111表示4个差分都相等,经过P变换后,可以确定四种情况(1、2、3、4个差分进行异或),当1、2个差分进行异或时,输出是唯一的(用“-”表示,对于其他情况也是一样),当3个异或时结果为1,当4个异或时结果为0。同样,如1112表示当1、2个差分进行异或时,结果唯一,任取3个异或时符号差分为1、4个差分异或时符号差分也为1,下面也用相同的方法表述。
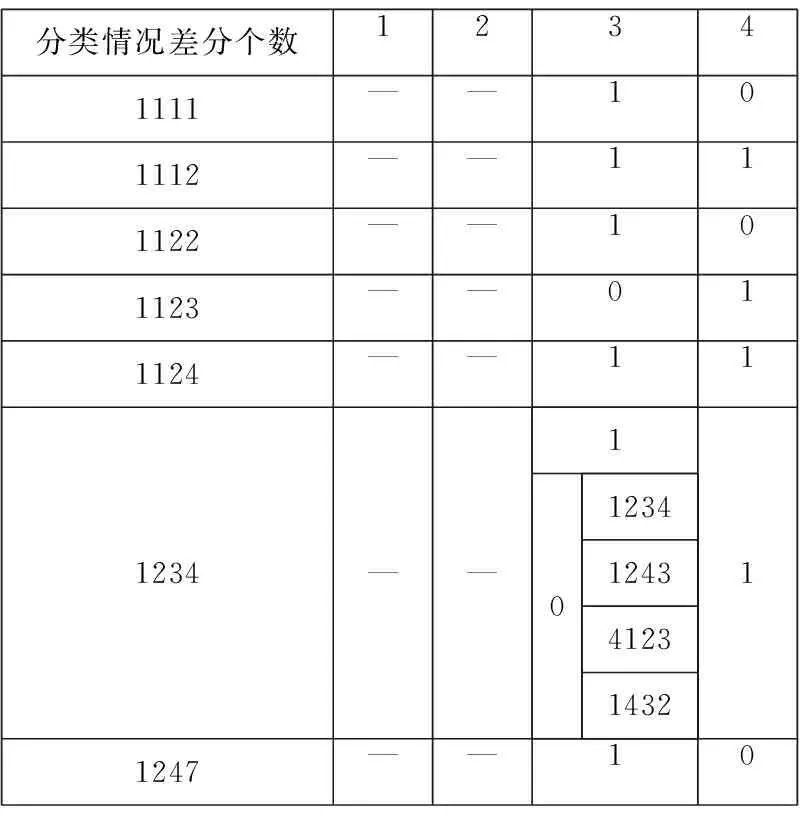
Table 2 Differential representation
注:1、2、3、4、7表示它们内部关系的符号差分,1、2、3存在关系式:1⊕2=3,4、7不存在内部的关系,这样就能把输入为4个活跃S盒的所有情况表示出来。
4 高概率自动化差分模式算法
本文借鉴符号差分的思想,考虑S盒性质。算法的核心思想是比较经过P置换或P逆置换后S盒两端对应零元位置是否相等(零元位置经过线性变换后具有唯一性),来过滤不满足的差分模式。下面给出了3、4轮算法的伪代码,我们搜索出MIBS的3、4轮最优迭代差分模式,进而给出迭代差分路径。
4.1 3轮迭代差分特征
Feistel-SP结构3轮迭代差分特征满足如下形式:
([Φ],[ΔX])
A:[ΔY]←[ΔX]
B:[ΔX]←[ΔY]
([ΔY],[Φ])
Feistel-SP3轮迭代差分结构如图2所示。
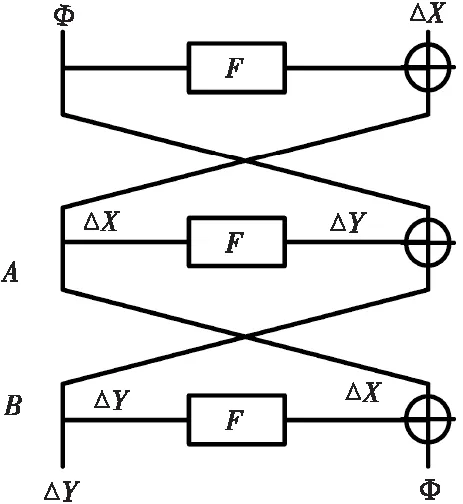
Figure 2 Differential structure of 3 round iteration
建立等式:
Sign(P-1(Δy))=
Sign(Δx)Sign(P-1(Δx))=Sign(Δy)
其具有对称性,利用这种性质我们设计了3轮迭代差分算法。
Feistel-SP结构3轮迭代模式算法伪代码如下:
1.差分变量ΔX、ΔY,联系关系为:Sign(P-1(Δy))=Sign(Δx),Sign(P-1(Δx))=Sign(Δy);
3. For选取输入差分ΔX的一种情况 do
4. For选取输出差分ΔY的一种情况 do
5. 分别对ΔX、ΔY求线性变换逆变变换存入临时变量TempX、TempY;
6. if(Sign(TempX)==Sign(ΔY)&&Sign(TempY)==Sign(ΔY)) Then
7. 找出最小活跃S盒个数,把满足条件的差分变量ΔX、ΔY存储起来,计数器加1;
8.Continue
以MIBS算法为例,基于上述算法我们搜索出所有的3轮迭代差分模式,遍历所有的迭代差分模式,搜索出3轮最优迭代差分特征,其最小活跃S盒个数为8,概率为2-20。下面列举了部分最优迭代差分模式和最优迭代差分路径数据。如表3和表4所示。
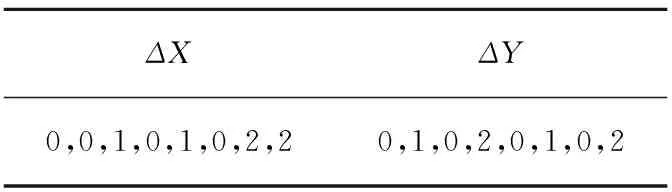
Table 3 Optimal differential mode for 3 rounds iteration
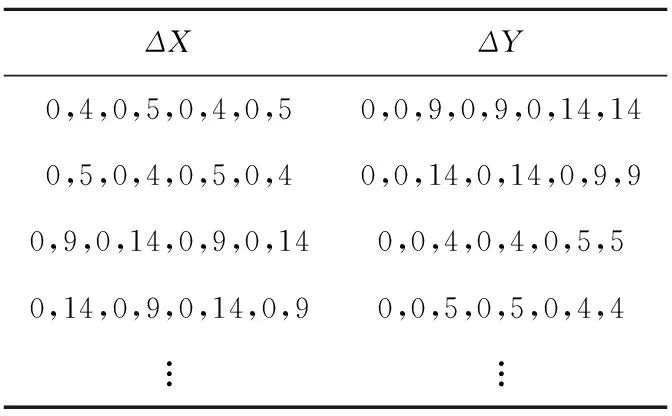
Table 4 Optimal differential path for 3 rounds iteration
4.2 4轮迭代差分模式特征
Feistel-SP结构4轮迭代差分特征满足如下形式:
A:([0],[ΔX])
B:[ΔY]←[ΔX]
C:[ΔX⊕ΔX′]←[ΔY]
D:[ΔY]←[ΔX′]
([ΔX′],[0])
Feistel-SP4轮迭代差分结构如图3所示。
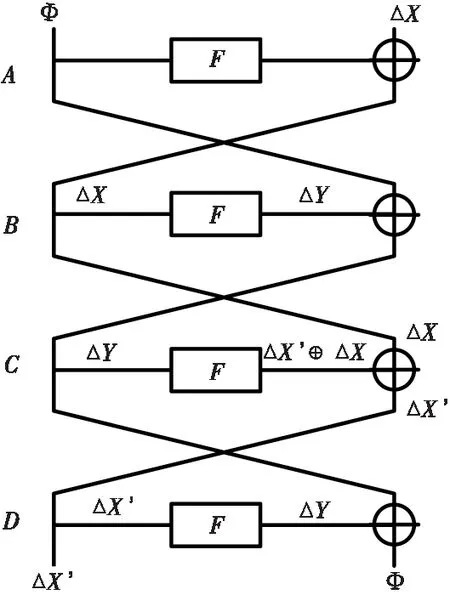
Figure 3 Differential structure of 4 round iteration
从特征B、D可以看出,Sign(ΔX)=Sign(ΔX′),且ΔX⊕ΔX′≠0,否则C轮的概率为0,我们发现4轮迭代特征中不可能只有一个活跃S盒,在此基础上构造出了4轮迭代差分模式的自动化搜索算法,进而搜索出概率最高的迭代差分特征。
Feistel-SP结构4轮迭代模式算法伪代码如下:
1.差分变量ΔX、ΔX′、ΔZ,联系关系为:Sign(ΔX′)=Sign(ΔZ);
3. For选取输入差分ΔX的一种情况 do
4. For选取输出差分ΔX′的一种情况 do
5. 分别对ΔX、ΔX′求线性变换逆变变换存入临时变量Temp_X、Temp_X′;
6.Z求线性正变换输出为ΔY;
7.if(Sign(Temp_X)==Sign(ΔY)&&Sign(Temp_X′)==Sign(ΔY)) Then
8. 找出最小活跃S盒个数,把满足条件的差分变量ΔX、ΔX′、ΔZ存储起来,计数器加1;
9.Continue
同样以MIBS算法为例,我们搜索出所有的4轮迭代差分模式,得到4轮最优迭代差分特征,其最小活跃S盒个数为11,概率为2-26。下面列举了部分最优迭代差分模式和最优迭代差分路径数据。表5为最优的迭代差分模式,表6为最优的迭代路径。
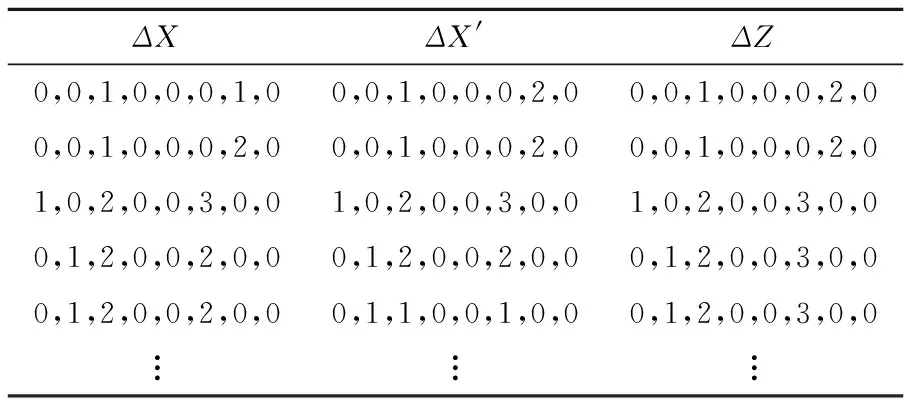
Table 5 Optimal differential mode for 4 rounds iteration

Table 6 Optimal differential path for 4 rounds iteration
5 结束语
本文提出了一种新的符号差分表示法,在此基础上构建了自动化搜索工具,应用于搜索MIBS分组密码的迭代差分模式,其方法对于其他总体结构是Feistel结构、轮函数是SP结构的分组密码也是适用的,例如Camellia和E2[9]等。对于Feistel-SP结构的分组密码,我们只要替换轮函数的线性部分,自动化搜索机就能找到3、4轮最优迭代差分模式和迭代差分特征。应用本文提出的自动化搜索技术,不仅能重新发现在字节上、比特位上的最大差分概率,还能找到其他未知的结果。这种攻击方法给算法的设计带来更多的启发,不仅有利于提升分组密码抵御差分分析的能力,而且有利于抵御其他攻击的分析方法。
为了能更好地完善自动化搜索工具,下一步工作我们会寻找Feistel-SP结构更加普遍的关系式,以便寻找出更多轮的最优迭代差分模式和迭代差分特征。
[1]FeistelH,WANotz,SmithJL.Somecryptographictechniquesformachine-to-machinedatacommunications[J].ProceedingoftheIEEE, 1975, 63(11):1545-1554.
[2]KandaM.PracticalsecurityevaluationagainstdifferentialandlinearcryptanalysesforfeistelcipherswithSPNroundfunction[C]∥ProcofSAC’00,2001:324-338.
[3]IzadiMI,SadeghiyanB,SadeghianS,etal.MIBS:Anewlightweightblockcipher[C]∥Procofthe8thInternationalConference,CANS’09, 2009:334-348.
[4]KandaM,MoriaiS,AokiK,etal.E2-Anew128-bitblockcipher[J].IEICETransactionsonFundamentalsofElectronics,CommunicationsandComputerSciences, 2000,E83-A(1):48-59.
[5]AokiK,IchikawaT,KandaM,etal.Camellia:A128-bitblockciphersuitableformultipleplatforms-designandanalysis[C]∥ProcofSAC’00, 2001:39-56.
[6]LiChao,SunBing,LiRui-lin.Attackmethodsandcaseanalysisofblockcipher[M].Beijing,SciencePublishingHouse, 2010.(inChinese)
[7]MatsuiM.LinearcryptanalysismethodforDEScipher[C]∥ProcofWorkshopontheTheoryandApplicationofCrytographicTechniquesonAdvancesinCryptology, 1994:386-397.
[8]LiChao,ShenJing.Differentialandlineariterativecharacteristicofcamellia[J].ChineseofJournalElectronics, 2005,33(8):1345-1348.(inChinese)
[9]NTT-NipponTelegraphandTelephoneCorporation.E2:Effcientencryptionalgorithm[EB/OL].[2013-05-13].http://info.isl.ntt.co.jp/e2.
附中文参考文献:
[6] 李超,孙兵,李瑞林.分组密码的攻击方法与实例分析[M].北京, 科学出版社,2010.
[8] 李超, 沈静.Camellia的差分和线性迭代特征[J].电子学报,2005,33(8):1345-1348.
LI Yan-jun,born in 1979,PhD,lecturer,her research interest includes design and analysis of block cipher.

方波(1989-),男,浙江杭州人,硕士生,研究方向为分组密码的自动化搜索技术。E-mail:bluepooh@126.com
FANG Bo,born in 1989,MS candidate,his research interest includes automated searching of block cipher.
Automated search of iterative differential mode with feistel-SP structure
LI Yan-jun1,FANG Bo1,2,MAO Ming1,2
(1.School of Telecommunications Engineering,Xidian University,Xi’an 710071;2.Beijing Electronic Science and Technology Institute,Beijing 100070,China)
Based on a new symbol differential representation,an automated search technique is presented,which can search out the optimal iterative differential mode of the block cipher with Feistel-SP structure.Selection of an appropriate mode can help find out all of the best iterative differential paths.The proposed method can not only greatly reduce the computational complexity,but also construct several rounds of optimal differential paths and find other unknown results. Based on the lightweight block cipher MIBS with automated search tools,the third and fourth optimaliterative differential paths of MIBS are found out, and the probabilities are 2-20and 2-26respectively.In addition,all the optimal iterative differential paths that meet the conditions are searched out.
Feistel-SP;MIBS;automated search;symbol differential;iterative differential
1007-130X(2015)03-0466-05
2013-11-18;
2014-03-01基金项目:中央高校基本科研业务费专项资金资助项目(1201120703,YQNJ1003)
TP393.84
A
10.3969/j.issn.1007-130X.2015.03.009

李艳俊(1979-),女,山西晋城人,博士,讲师,研究方向为分组密码设计与分析。E-mail:Lyj@besti.edu.cn
通信地址:100070 北京市丰台区富丰路7号北京电子科技学院
Address:Beijing Electronic Science and Technology Institute,7 Fufeng Rd,Fengtai District,Beijing 100070,P.R.China

