基于均匀免疫优化算法的最大团问题求解*

汪宏海，张正球

(1.西安电子科技大学计算机学院,陕西 西安 710071；2.赣州师范高等专科学校计算机系,江西 赣州 341000；

3.福建师范大学软件学院,福建 福州 350027)

基于均匀免疫优化算法的最大团问题求解*

汪宏海1,2，张正球3

(1.西安电子科技大学计算机学院,陕西 西安 710071；2.赣州师范高等专科学校计算机系,江西 赣州 341000；

3.福建师范大学软件学院,福建 福州 350027)

最大团问题是一种典型的组合优化问题，具有广泛的应用背景。针对最大团问题的NP特性，提出了一种基于免疫克隆优化的智能求解算法。描述了最大团问题的数学模型，设计了求解最大团问题的抗体编码、亲和度函数、变异算子及抗体修正方法。在免疫克隆参数设置时，将其描述为多因素多水平的均匀设计，减少了设置参数的实验次数。通过最大团问题的基准算例进行了实验。结果表明，本算法求解效果较好，并且求解速度较快。

免疫优化；最大团问题；抗体编码；均匀设计

1 引言

最大团问题MCP(Maximum Clique Problem)是图论中的一个经典组合优化问题，也称为最大独立集问题[1]。MCP在市场分析、方案选择、计算机视觉、故障诊断等领域具有非常广泛的应用。因此，研究最大团问题具有较高的理论价值和现实意义。

最大团问题是一类典型的NP完全问题。目前，求解MCP问题的算法主要分为两类：确定性算法和启发式智能算法[2,3]。常见的确定性算法有分支限界算法和回溯算法等[4～7]，确定性算法要求在有效的时间内给出最大团问题的最优解，而非确定性的算法并不保证最终给出的是最优解。由于最大团问题是 NP完全问题，当无向图规模较大时，寻找最大团的时间复杂度较高[8～11]。已有的研究表明，非确定性算法中的智能优化算法是求解NP完全问题的有效算法。

人工免疫系统是受生物免疫系统机制启发的一种智能计算系统，克隆优化算法是人工免疫系统的主要算法之一，已经在优化、智能控制、数据处理等多个领域得到广泛应用[12,13]。基于此，本文采用免疫克隆算法求解最大团问题，并在免疫参数设置时，描述为均匀设计问题(本文称为均匀免疫优化算法)。实验结果表明，算法求解效果较好。

2 问题描述

2.1 最大团问题描述

最大团是图论中的一个经典问题，可描述为:从图G中找到一个顶点最多的完全子图(完全子图即是指图中的任意两点都有边相连)。

设无向图G=(V,E),G的顶点集合V=(V1,V2,…,Vn), 其中，n=|V|为V所含的顶点个数，E=(Vi,Vj)为G的边集合。设顶点子集合S⊆V,G(S)为由S导出的G的生成子图。若G(S)的顶点两两相连，则称G(S)为G的团。在G的所有团中, 包含顶点最多的团是G的最大团。最大团问题的目标就是寻找给定图的最大团。

2.2 最大团问题的数学模型

最大团问题可以用一个0-1分配模型来描述[3,11]：

s.t.xi+xj≤1,∀(Vi,Vj)∈E;

xi∈(0,1),i=0,1,2,…,n

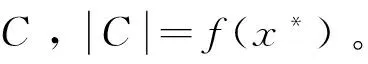
3 算法关键实现技术

免疫优化是人工免疫系统的主要算法之一，是一种得到广泛应用的智能优化算法。使用免疫克隆算法求解问题时，抗体代表问题的解，算法通过相关的免疫克隆、变异算子对抗体进行演化，最终找到问题的最优解。

免疫克隆算法基本过程简述如下：

(1)将求解问题转化为抗体编码表示。

(2)抗体种群的初始化，即生成一定数量满足问题的解。

(3)计算抗体种群中各个抗体的亲和度。

(4)对亲和度高的抗体进行克隆操作。

(5)对克隆生成的抗体进行相应的变异操作。

(6)若当前解满足要求，则算法结束，输出最终结果；否则，转步骤(3)继续。

基于免疫的最大团问题实现中，几个关键技术说明如下。

3.1 抗体编码技术

最大团问题中，图G用邻接矩阵A表示，如果i、j之间有边，则邻接矩阵中的对应元素为1，否则为0。抗体x=[x1,x2,…,xi,…,xn]表示图G中的一个可能的最大团，用0、l组成的行向量表示，其列数与A相等。x中的元素等于l，表示图G的相应点属于这个可能的最大团。例如：x=[010101010]，表示图顶点集V= {1,2,3,4,5,6,7,8,9}的一个子团S= {2,4,6,8}。

3.2 亲和度函数

3.3 自适应克隆

克隆操作是免疫优化的主要操作之一，影响着算法的收敛速度和性能。这里采用一种按亲和度的大小进行自适应克隆的机制，保证具有较高亲和度的优秀抗体进化到下一代的机率加大。具体说明如下：

假设选出的s个抗体按亲和度值升序排序为：M1(g),M2(g),…,Ms(g)，则对第i个抗体Mi(g)(1≤i≤s)的qi克隆产生的抗体数目为：

第g代克隆产生的抗体种群总个数为：

其中，Int(*)表示向上取整，nt(nt>s)表示克隆控制参数，f(*)代表亲和度函数的计算。

3.4 变异算子

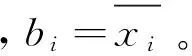
3.5 抗体修正

由于抗体变异后可能产生非法解,因此需要进行抗体修正操作，使其合法化。基于连接矩阵，对抗体进行遍历，找出对应子图的连接矩阵，删除度最小的节点(即基因位1变0)，使其成为合法抗体。具体如下：逐一检查x中的元素，如果xi等于1，逐一检查xi之后等于1的元素是否与xi存在边，如果不存在边，该元素由l改为0。

3.6 均匀设计

均匀设计是一种解决多因素、多水平实验问题的有效方法，以通过最少的实验来获得最多的信息，实验次数比正交设计法明显减少[14]。

一般地，如果有N个因素，且每个因素有Q个水平，则共有QN种组合。当N和Q比较大时，则取全部的组合进行实验是不可能的。因此，需要选择数量较少、具有代表性的因素水平组合做样本。均匀设计方法正是这样的一种策略，可以有效减少实验的次数[14]。由于免疫优化算法的参数设置需要通过实验调整，为了减少实验次数，本文采用均匀设计完成参数的取值，具体过程见实验部分。

3.7 算法实现步骤

本文设计的免疫克隆优化算法实现步骤如下：

步骤1 根据编码方式初始化种群，设进化代数为g，令g=0。

步骤2 计算所有个体的亲和度,亲和度函数为子团中顶点数目,函数值越大，抗体越好。

步骤3 以进化代数g作为终止条件，判断是否满足结束条件。如果满足结束条件,则终止程序，输出最优解；否则,转步骤4。

步骤4 根据各个抗体的亲和度值，进行克隆扩增操作。克隆采用自适应克隆(2.3节所示)，即亲和度高的抗体克隆数目较多。

步骤5 对克隆种群进行2.4节所示的变异操作。

步骤6 对抗体进行2.5节所示的修正操作。

步骤7g=g+1,转步骤2。

4 仿真实验与结果分析

4.1 免疫克隆算法的参数设置

免疫克隆算法的参数设置通常是依靠经验和实验来确定的,因此实验工作量大且难以得到最优的参数组合[15]。本文将免疫算法的参数设定问题描述成均匀设计中多因素、多水平的实验设计,从而能够用较少的实验设定参数的取值。均匀设计中的最大因素数即为免疫克隆算法的参数个数，水平数即为每个参数的取值范围。本文中，克隆选择算法的参数主要有变异概率pm、克隆比例系数k和种群规模M。

基本克隆选择算法的三个参数(s=3),若每个参数取10个值(t=10)。使用均匀设计设置算法参数的步骤简述如下:

(1)对s=3个参数分别确定取值范围；

(2)对每个参数取t=10个水平,根据均匀设计的推荐表,得到Ut(ts)；

(3)根据均匀表编制实验方案,找出对应的参数组合,对每组进行多次实验,统计其数据,找出最优的组合。

本文中，设置种群规模、变异概率、克隆系数的范围分别为[30,80]、 [0.35,0.85]、[2,4], 经过均匀设计实验，最终参数取值如下：种群M=60，pm=0.3，克隆系数k=2，最大进化次数200次。

4.2 算法实验结果

采用Matlab7.0对DIMACS[16]提供的标准算例进行实验。为避免算法的随机性，对每个算例在同一台机器上进行连续100次计算，其中，sbest表示100次运行中求得的最好解；savg表示100次运行所得解的平均值；σ为标准差；tavg为100次运行中找到最好解的平均用时(秒)；gavg为收敛代数的平均值；s为100次运行中找到最好解的次数。结果如表1所示。实验结果采用文献[2]与文献[5]作为对比算法，二者均是采用启发式智能算法的经典文献，与本文算法有可比较性。

从表1可看出，本文算法对每个算例都能够100%搜索到最好解，而文献算法只有部分最好解，而且本文算法在很多衡量指标上，如解的平均值、标准差、找到解的时间、成功次数上均好于文献算法。

具体而言，在数据规模较小时，各种算法找到的最优解sbest相同，但当规模较大时，本算法具有一定的优势。此外，本文算法找的savg值优于相关算法，100次运算中找到最好解的次数较多； 100次运行中找到最好解的平均用时相对较短；gavg收敛代数平均值较小。实验结果说明本文算法取得了较好的求解效果。

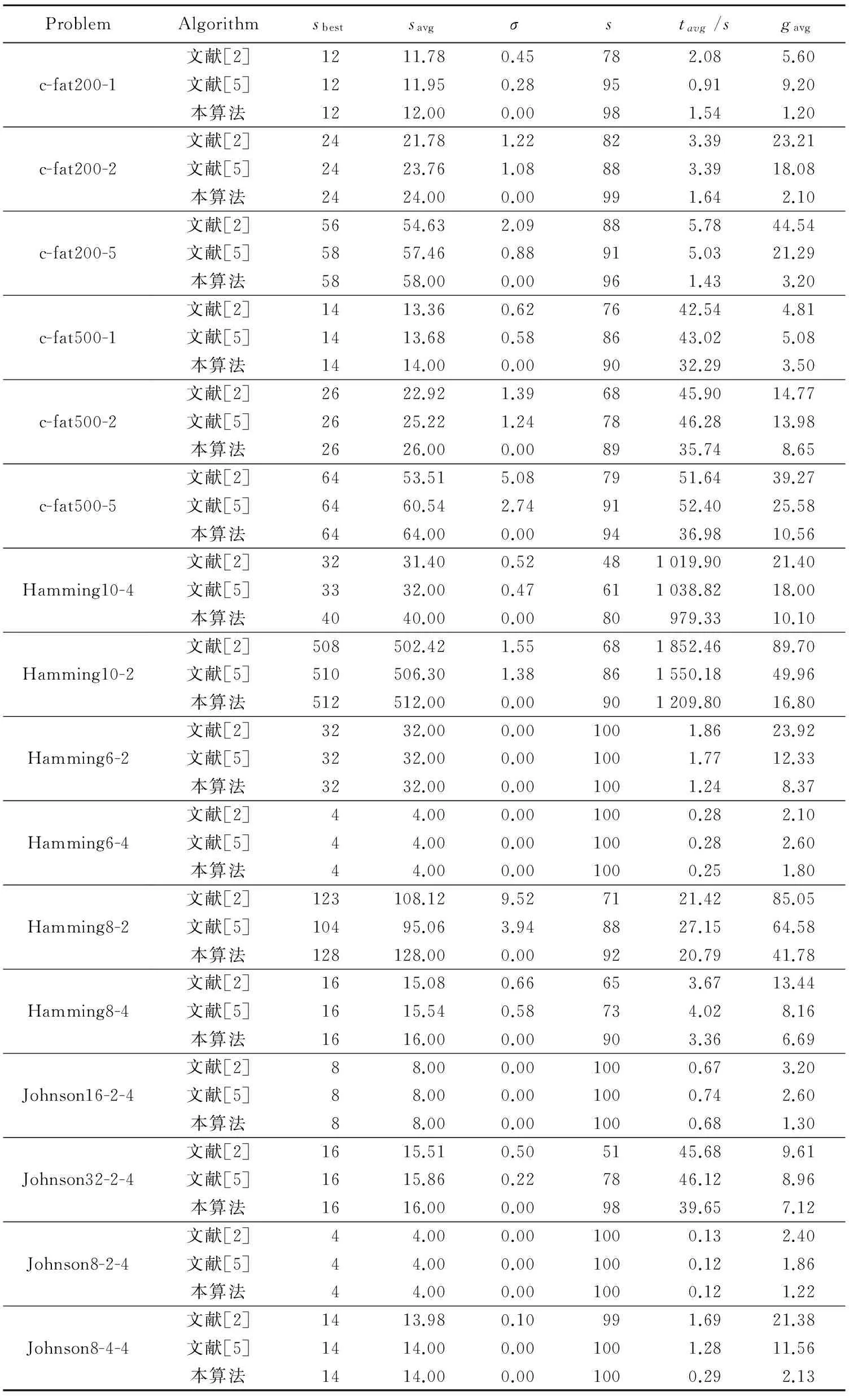
Table 1 Experiment results of MCP

4.3 算法复杂度分析

最大团中顶点个数为n=|V|，免疫优化算法中，抗体的种群规模为M，则基于免疫的最大团问题求解中，算法的最好时间复杂度为O(n*M)(当图为低度图时)；最坏情况下，算法的时间复杂度为O(M*n3)，是可以接受的。

5 结束语

最大团问题是一类经典的组合优化问题，有着广泛的工程应用基础。基于最大团问题的NP特性，本文采用免疫克隆优化算法进行求解。同时，为了减少实验设置次数，采用了均匀设计方法。通过标准实验进行验证，结果表明，算法求解效果较好，具有一定的优势。

[1] Fan Yue-ke,Qiang Xiao-li,Xu Jin. Sticker model for maximum clique problem and maximum independent set[J]. Chinese Journal of Computers,2010,33(2)：855-864.(in Chinese)

[2] Zhang Yan,Dang Qun,Huang Yong-xuan. A Memetic algorithm based on match-crossover for the maximum clique problem[J].Control and Decision,2010,25(9):213-219.(in Chinese)

[3] Zhou Yan-tao, Li Ken-li, Luo Xing.An algorithm for solving maximum clique problem based on self-assembly model of DNA[J].Journal of Hunan University(Naturnal Science), 2012,44(9):9-25.(in Chinese)

[4] Pan Quan,Guo Ming,Lin Peng.Largest group based on MapReduce algorithm [J]. Systems Engineering Theory and Practice, 2011,23(10):10-15.(in Chinese)

[5] Singh A,Gupta A K. A hybrid heuristic for the maximum clique problem [J].Journal of Heuristics,2006,12(6):5-22.

[6] Zhou Kang,Liu Shuo,Qin Lei, et al.Sticker model-based DNA algorithm of maximum clique problem[J].Journal of Huazhong University of Science and Technology(Nature Science), 2010,21(9):9-15.(in Chinese)

[7] Li Ken-li,Zhou Xu,Zou Shu-ting. Improved volume molecular solutions for the maximum clique problem on DNA-based supercomputing[J].Chinese Journal of Computers, 2008,41(12):12-15.(in Chinese)

[8] Pullan W,Hoos H H.Dynamic local search for the maximum clique problem[J]. Journal of Artificial Intelligence Research, 2006 (25):159-185.

[9] Lü Qiang,Bai Zhan-hua, Xia Xiao-yan.Leader-based parallel cross entropy algorithm for maximum clique problem[J].Journal of Software, 2008,34(11):11-15.(in Chinese)

[10] Katayama K,Hamamoto A, Narihisa H. An effective local search for the maximum clique problem[J].Information Processing Letters, 2005, 95(5):503-511.

[11] Pullan W.Approximating the maximum vertexedge weighted clique using local search[J]. Journal of Heuristics, 2008,14(2):117-134.

[12] Gong M G,Jiao L C,Zhang L N, et al. Immune secondary response and clonal selection inspired optimizers[J].Progress in Natural Science,2009,19(2):237-253.

[13] Gong Mao-guo,Jiao Li-cheng,Liu Fang,et al. Memetic computation based on regulation between neural and immune systems:The framework and a case study[J].Science China (Information Science),2010,45(11):2131-2138.

[14] Fang Kai-tai, Ma Chang-xing. Orthogonal and uniform design[M]. Beijing:Science Press, 2009.(in Chinese)

[15] Yu Hang,Jiao Li-cheng,Gong Mao-guo,et al.Clonal selection function optimization based on orthogonal experiment design[J].Journal of Software, 2010, 21(5):950-967.(in Chinese)

[16] DIMACS[EB/OL].[2012-12-13].ftp://dimacs.rutgers.edu/pub/challeng/.

附中文参考文献:

[1] 范月科,强小利,许进.图的最大团与最大独立集粘贴DNA计算模型[J].计算机学报，2010，33(2)：855-864.

[2] 张雁, 党群, 黄永宣.一种基于匹配交叉求解最大团问题的Memetic算法[J].控制与决策,2010,25(9):213-219.

[3] 周炎涛,李肯立,罗兴.一种基于DNA自组装模型求解最大团问题的算法[J].湖南大学学报(自然科学版),2012,44(9):9-25.

[4] 潘全,郭鸣,林鹏.基于MapReduce的最大团算法[J].系统工程理论与实践,2011,23(10):10-15.

[6] 周康,刘朔,覃磊,等.基于粘贴模型的最大团问题算法[J].华中科技大学学报(自然科学版),2010,21(9):09-15.

[7] 李肯立,周旭,邹舒婷.一种改进的最大团问题DNA计算机算法[J].计算机学报, 2008,41(12):12-15.

[9] 吕强,柏战华,夏晓燕.一种求解最大团问题的并行交叉熵算法[J].软件学报, 2008,34(11)：11-15.

[14] 方开泰,马长兴.正交与均匀试验设计[M].北京:科学出版社,2009.

[15] 余航,焦李成,公茂果,等.基于正交试验设计的克隆选择函数优化[J].软件学报,2010, 21(5):950-967.

WANG Hong-hai,born in 1977,PhD,associate professor，his research interests include wireless network, and optimization algorithm.

张正球(1978-),男，江西临川人，硕士生，讲师，研究方向为计算智能、网络安全和优化算法。E-mail:zzqiu_2008@163.com

ZHANG Zheng-qiu,born in 1978,MS candidate,lecturer，his research interests include computational intelligence,network security, and optimization algorithm.

A uniform immune clone based intelligent optimization algorithm to solve the maximum clique problem

WANG Hong-hai1，2，ZHANG Zheng-qiu3

(1.School of Computer,Xidian University,Xi’an 710071;2.Department of Computers Science,Ganzhou Teachers Colleage,Ganzhou 341000;3.Faculty of Software,Fujian Normal University,Fuzhou 350027,China)

The maximum clique problem is a typical combinatorial optimization problem,which has wide application background.For the NP characteristic of the maximum clique problem, an immune clone based on intelligent optimization algorithm is proposed to solve it. The mathematical model of the maximum clique problem is described.For solving the maximum clique problem,antibody encoding, affinity function, mutation operator and antibody correction method are designed. To reduce the number of parameter setting for the experiment, it is converted into a uniform design problem of multi-factor and multi-level.The Benchmark experimental results show that the algorithm has better performance and rapid solving speed.

immune optimization;maximum clique problem;antibody encoding;uniform design

1007-130X(2015)03-0534-05

2013-11-01;

2014-02-24基金项目：福建省教育厅JK类科技资助项目(JK2010010)；福建省自然科学基金资助项目(2011J01339)

TP18

A

10.3969/j.issn.1007-130X.2015.03.021

汪宏海(1977-),男，江西樟树人，博士，副教授，研究方向为无线网络和优化算法。E-mail:redsea54@163.com

通信地址：341000 江西省赣州市经济技术开发区高校园区35号

Address:No 35,Economic and Technological Development Zone,Ganzhou 341000,Jiangxi,P.R.China