一种高效用项集并行挖掘算法*

宋 威，吉红蕾，李晋宏

(北方工业大学计算机学院，北京 100144)

一种高效用项集并行挖掘算法*

宋 威，吉红蕾，李晋宏

(北方工业大学计算机学院，北京 100144)

由于能反映用户的偏好，可以弥补传统频繁项集挖掘仅由支持度来衡量项集重要性的不足，高效用项集正在成为当前数据挖掘研究的热点。为使高效用项集挖掘更好地适应数据规模不断增大的实际需求，提出了一种高效用项集的并行挖掘算法PHUI-Mine。提出了记录挖掘高效用项集信息的DHUI-树结构，描述了DHUI-树的构造方法，论证了DHUI-树的动态剪枝策略。在此基础上，给出了高效用项集挖掘的并行算法描述。实验结果表明，PHUI-Mine算法具有较高的挖掘效率及较低的存储开销。

数据挖掘；高效用项集；并行算法；动态高效用项集树

1 引言

传统的关联规则挖掘假设用户只对频繁发生的项集感兴趣，平等地对待每一事务和项目，不管各个事务、项目在效用上有多大差异[1, 2]。但是，事实上，项目之间的确存在着效用的差异，如商家显然不会同等对待一件珠宝首饰和一块面包。因此，基于支持度的频繁集挖掘已很难满足用户获取不完全依赖于频率的重要项集的需求。为解决这一问题，高效用项集挖掘[3, 4]应运而生，并正在成为频繁模式挖掘的热点问题之一。

2004年，Yao H等[3]最先提出了高效用项集问题及MEU算法。MEU算法使用启发式策略来判断项集是否为候选高效用项集，但在使用这种启发策略所得到的候选项集中，高效用项集所占的比例较小，造成了巨大的存储与计算开销。

2005年，Liu Y等[4]提出了挖掘高效用项集的Two-Phase算法。该算法引入了高事务加权效用项集的概念，并论证了高事务加权效用项集不仅是高效用项集的超集，而且满足频繁项集挖掘中的反单调性[1]。这样，Two-Phase算法将高效用项集挖掘分为两个阶段：先利用反单调性挖掘全体高事务加权效用项集；再通过扫描数据库来计算高事务加权效用项集的真实效用值，进而得到全体高效用项集。2008年，Li Y-C等[5]提出了两种高效用项集挖掘算法FUM和DCG+，通过引入新的剪枝策略来减少高事务加权效用项集的数量。但是，与Two-Phase一样，这些方法依然使用逐层产生候选项集再验证的策略，需要反复扫描数据库。

近年来，学者们提出了各种新的高效用项集挖掘算法，如：基于投影的方法[6, 7]、基于数据库垂直表示的方法[8]、基于效用列表的方法[9]、模式增长的方法[10, 11]等，这些方法有效地减少了扫描数据库的次数、高事务加权效用项集的数量，提高了挖掘效率。但是，现有的绝大多数高效用项集挖掘算法都是串行的，随着真实世界数据规模越来越庞大，各种挖掘任务对处理的响应效率要求越来越高，提出并行的高效用项集挖掘算法已势在必行。

本文引入动态高效用项集树DHUI-树(Dynamic High Utility Itemset Tree)结构来记录高效用项集挖掘的信息，进而给出了新的高效用项集剪枝策略。在此基础上，提出了一种基于动态裁剪树型结构的高效用项集并行挖掘算法PHUI-Mine(Parallel High Utility Itemset Mine)。实验结果表明，该算法挖掘效率较高、存储开销较小。

2 问题描述

设I={i1,i2,…,im}为项目集合，其中每个项目ip∈I(1≤p≤m)都有唯一的利润值p(ip)。项目的集合称为项集，含有k个项目的项集称作k-项集。为简单起见，把项集{i1,i2,…,ik}记为i1i2…ik。D={T1,T2,…,Tn}为事务数据库，每一事务Td∈D都是I的一个子集，有唯一的标识TID。事务Td中的每个项目ip都有一个数量q(ip,Td)，表示项目ip在事务Td中出现的次数。项目ip在事务Td中的效用定义为：u(ip,Td)=p(ip)×q(ip,Td)。

项集X在事务Td中的效用定义为：

(1)

项集X在数据库D中的效用定义为：

(2)

给定项集X及用户指定的最小效用阈值min_util，若u(X)≥min_util，则称X为高效用项集；否则，称X为低效用项集。给定事务数据库D和最小效用阈值min_util，挖掘高效用项集也就是发现所有效用值不低于min_util的项集。

由于高效用项集的挖掘不再满足频繁项集挖掘中通常使用的Apriori性质，为提高挖掘效率，Liu Y等[4]提出了事务加权向下闭合的策略，利用反单调性来挖掘高效用项集的超集，再通过一遍扫描数据库得到所有高效用项集。

事务Td的事务效用定义为：TU(Td)=u(Td,Td)。项集X的事务加权效用定义为：

(3)

若TWU(X)≥min_util，则称X为高事务加权效用项集；否则，称X为低事务加权效用项集。

定理1[4]若项集X不是高事务加权效用项集，则X的任何超集都不是高事务加权效用项集。

给定项集X，称g(X)={t∈D|∀i∈X,i∈t}为X的支持集。定义X的支持度计数为count(X)=|g(X)|。支持度计数将在3.3节中用于对树型结构进行剪枝。

例1 表1是一个示例数据库，其中每个项目的利润值如表2所示。项目E在事务T2中的效用为：u(E,T2)=2×1=2，项集BE在事务T2中的效用为：u(BE,T2)=u(B,T2) +u(E,T2)=10+2=12。T2的事务效用为TU(T2)=u(ABDE,T2)=25，项集BE的事务加权效用TWU(BE)=TU(T2)+TU(T4)+TU(T5)=74，而项集BE在示例数据库中的效用为u(BE)=u(BE,T2)+u(BE,T4)+u(BE,T5)=12+14+20=46。给定min_util=35，由于TWU(BE)>min_util且u(BE)>min_util，故BE既是一个高事务加权效用项集，也是一个高效用项集。由于BE被T2、T4和T5三条事务所包含，故其支持度计数count(BE)=3。

Table 1 Example database

Table 2 Profit table

3 DHUI-树结构

3.1 DHUI-树的元素

为实现并行挖掘高效用项集，我们在每个站点保存一棵树型结构。

定义1(动态高效用项集树(DHUI-树))T是一种按如下方式定义的树结构：

(1)它包含一个标记为null的根节点，记作T.root；一个项目前缀子树的集合，记作T.tree；一个高事务加权效用项目头表，记作T.header。

(2)项目前缀子树T.tree中的每个节点至少包含六个域：item、count、util、node-link、children以及parent。其中：item表示节点代表的项目；count表示包含从根节点到本节点的路径上所有项目的事务数目；util表示从根节点到本节点的路径上项目item的事务加权效用；node-link指向树中下一个与本节点具有相同item的节点；children代表本节点所有的孩子节点；parent指向本节点的父节点。

(3)高事务加权效用项目头表T.header中的每行至少存储四个域：item、No、TWU、node-link。其中：item表示该行对应的项目；No表示包含项目item的事务数目的变化，初始值为item的支持度计数，即count(item)；TWU代表item的事务加权效用，即TWU(item)；node-link指向树中第一个表示项目item的节点。

定义2 在DHUI-树T中，项集X的一个条件模式为CP(X)=(Y:num,util)，其中YX是从根节点T.root到项集X的一条分支，num是X在该分支上的支持度计数，util是该分支上项集X的事务加权效用。称项集X的全部条件模式的集合为X的条件模式基，记作CPB(X)。由X的条件模式基构建的动态高效用项集树称为X的条件DHUI-树，记作CT(X)。

3.2 DHUI-树的构造

DHUI-树的构造基于模式增长[12]策略。具体而言：首先将高事务加权效用项目按照TWU由高到低的顺序排列，构成DHUI-树的高事务加权效用项目头表。接下来依次处理数据库中的每条事务，删去事务中的低事务加权效用项目，并将剩余项目按照TWU由高到低的顺序排列，将事务中的项目依次插入DHUI-树：若当前节点n存在代表项目为待插入项目i的子节点m时，累加m.count和m.util；否则，创建节点n的孩子节点p，使得p.item=i，并记录p.count和p.util，将树中上一个代表项目i的节点与p连接起来。

Table 3 Re-organized example database

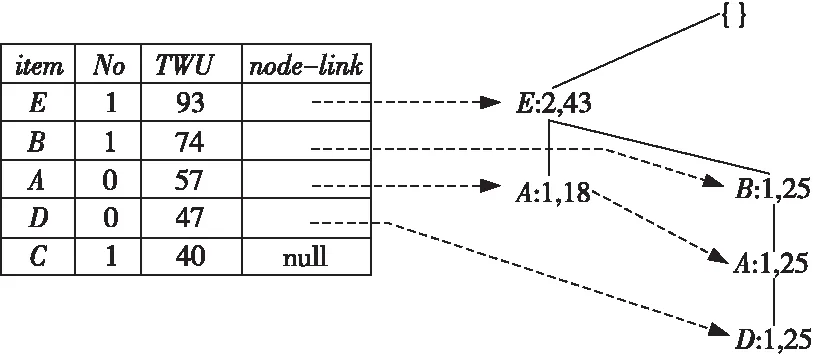
3.3 DHUI-树的动态剪枝

为快速挖掘高效用项集，利用DHUI-树T的头表T.header中No域的变化，对DHUI-树进行动态剪枝，达到了边构造DHUI-树边挖掘高效用项集的效果。

具体而言，当某个高事务加权效用项目item插入DHUI-树T后，DHUI-树T的头表T.header中No(item)减1，若No(item)减为0，就可以对代表item的节点及其子节点剪枝，并开始挖掘包含item的高效用项集。

定理2 给定DHUI-树T及其中的项目i，N={n1,n2,…,nk}是T.tree中包含i的节点集合。在构造(条件)DHUI-树T的过程中，若头表T.header中i对应的No域的值减为0，则在T的后续构造过程中，N中的节点不会发生变化，其后代节点所包含项目的条件模式不会发生变化。

证明 若T.header中i对应的No域的值减为0，则说明T.tree中包含i的节点均已构造完毕，这些节点的集合就是N，在T的后续构造过程中N中的节点不会再发生变化。

对∀n∈N，分如下两种情况讨论：

(1)若n是叶子节点，则n没有后代节点。

(2)若n不是叶子节点，由于n不会再发生变化，由DHUI-树的构造过程可知，不会再有项目作为n的后代添加到T中来，由定义2可知，它们的条件模式也不会发生变化。

□

根据定理2，在DHUI-树T的构造过程中，一旦T.header中某个项目i的支持度计数减为0，便可将与i对应的节点及其后代进行剪枝，并开始挖掘含有i的高效用项集。

4 并行挖掘算法PHUI-Mine

并行挖掘算法PHUI-Mine分为两个阶段：第一阶段是挖掘全局高事务加权效用项目；第二阶段是分站点挖掘全体高效用项集。

4.1 计算全局高事务加权效用项目

算法1 计算全局高事务加权效用项目

输入:数据库D，最小效用阈值min_util。

输出:全局高事务加权效用项目。

步骤2for每个站点Sido

步骤3for每个项目ido

步骤4 计算TWU(i)，并发送给其它n-1个站点；

步骤5endfor

步骤6 接收来自其它n-1个站点的项目事务加权效用；

步骤7 计算全局高事务加权效用项目；

步骤8endfor

4.2 并行挖掘高效用项集

假设经算法1处理后，共得到n个全局高事务加权效用项目，则共需要n个站点并行挖掘高效用项集。记挖掘含项目i的高效用项集的站点为Si，记站点Si要处理的数据库为Di。在并行挖掘高效用项集阶段，由于每个站点执行的算法是一致的，因此只给出一个站点的算法。

算法2 并行挖掘高效用项集

输入:最小效用阈值min_util。

输出:高效用项集。

步骤1forDi中的每条事务Trdo

步骤2 删除低事务加权效用项目，按事务加权效用由高到低的顺序排列高事务加权效用项目；

步骤3if项目i存在于Tr中then

步骤4 将Tr插入站点Si的DHUI-树Ti；

步骤5 No(i)--；

步骤6ifNo(i)==0then

步骤7forDHUI-树中的每个节点ndo

步骤8ifn.item==ithen

步骤9 计算CP(i)，构建CT(i)；

步骤10 HTW-growth(i, CT(i));

步骤11 在Ti中对n及其后代节点剪枝；

步骤12endif

步骤13endfor

步骤14endif

步骤15endif

步骤16forTr中i之外的每个项目itemdo

步骤17 将Tr发送给站点Sitem；

步骤18endfor

步骤19endfor

步骤20for其它站点发来的每条事务Tkdo

步骤21 将Tk插入站点Si的DHUI-树Ti；

步骤22 No(i)--；

步骤23ifNo(i)==0then

步骤24forDHUI-树中的每个节点ndo

步骤25ifn.item==ithen

步骤26 计算CP(i)，构建CT(i)；

步骤27 HTW-growth(i, CT(i));

步骤28 在Ti中对n及其后代节点剪枝；

步骤29endif

步骤30endfor

步骤31endif

步骤32endfor

步骤33 计算包含项目i的高事务加权效用项集的实际效用；

步骤34 输出包含项目i的高效用项集；

ProcedureHTW-growth(项集X, 条件DHUI-树CT(X))

步骤1ifCT(X)只包含一个分支Bthen

步骤2forB的每个子集Ydo

步骤3 输出Y∪X，TWU(Y∪X)与Y中所包含节点的最小TWU相等；

步骤4endfor

步骤5elsefor每个i∈CT(X).headerdo

步骤6 HTW-growth(X∪{i}, CT(X∪{i});

步骤7endfor

步骤8endif

5 性能评测

5.1 实验环境与数据集

性能评测的硬件平台是Intel双核2.8GHzCPU，2GB内存，操作系统是WindowsXP，编译器是VisualStudio2010，通过多线程的方式来模拟并行算法中的多个站点。

大量文献表明，高效用项集挖掘算法的研究重点主要集中在如何提高基于内存的算法的挖掘效率，极少有高效用项集的并行挖掘算法[13, 14]。主要原因在于这些方法缺少适合于并行化的数据结构，这也正是本文研究的出发点。因此，把本文提出的PHUI-Mine并行挖掘算法与两种主流的串行高效用项集挖掘算法Two-Phase[4]和HUC-Prune[10]进行了对比实验。在早期的频繁模式并行挖掘的研究过程中，在缺少合适的并行对比算法的情况下，也曾使用过串行算法进行性能比较[15, 16]。

实验所使用的数据集及其特性如表4所示，这些数据集可由FIMI资源库下载(http://fimi.cs.helsinki.fi/)。

Table 4 Characteristics of datasets

由于这些数据均不包含项目的利润值及在不同事务中出现的次数，为适用于高效用项集挖掘，对数据做了如下处理：(1)为每条事务中的每个项目随机产生一个1～5的整数作为出现次数；(2)为每个项目随机产生一个1.0～10.0的实数作为利润值。与其它方法[4, 10]一样，我们产生的利润值服从对数正态分布(Log Normal Distribution)。

5.2 运行时间对比

我们首先比较了三种算法在三个数据集上的运行效率，如图3～图5所示。

Figure 3 Comparison of execution time on T10D20k among three algorithms

Figure 4 Comparison of execution time on Mushroom among three algorithms

由图3和图4可以看出，在T10D20k和Mushroom两个数据集上，算法PHUI-Mine和HUC-Prune的运行时间均随着最小效用阈值的降低而增加。在T10D20k数据集上，PHUI-Mine平均比HUC-Prune快59%，在Mushroom数据集上，PHUI-Mine平均比HUC-Prune快43%。Two-Phase算法在这两个数据集上的运行时间有一定的波动性。在T10D20k数据集上，PHUI-Mine平均比Two-Phase快79%，在Mushroom数据集上，PHUI-Mine平均比Two-Phase快51%。

Figure 5 Comparison of execution time on BMS-POS among different algorithms

由图5可以看出，当最小效用阈值在68%～80%时，PHUI-Mine的运行效率优于Two-Phase和HUC-Prune。三种算法在BMS-POS数据集上运行时间较为稳定的原因在于，尽管BMS-POS数据集的记录数较多，但其每条记录都非常短，属于极为稀疏的数据，因此算法的性能随最小效用阈值变化的趋势不明显。

5.3 内存消耗对比

我们还比较了三种算法在三个数据集上的内存消耗，如图6～图8所示。

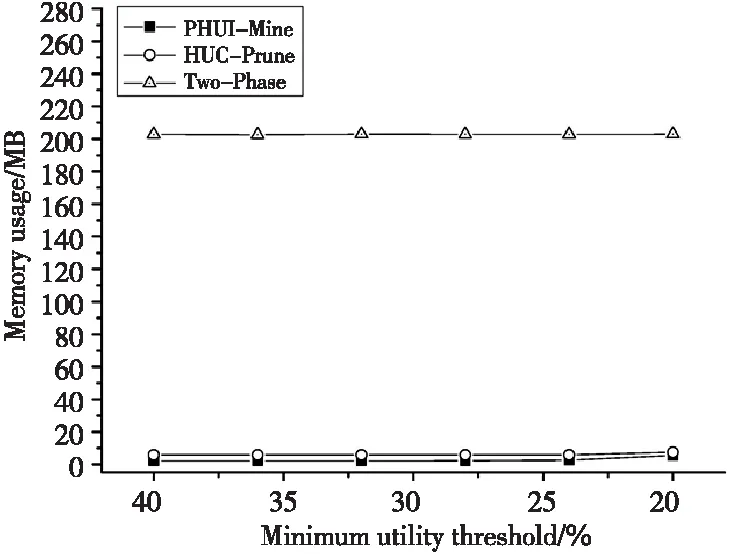
Figure 6 Comparison of memory usage on T10D20k

Figure 7 Comparison of memory usage on Mushroom

Figure 8 Comparison of memory usage on BMS-POS

由图6～图8可以看出，在三个数据集上，三种算法的内存消耗基本都保持在较平稳的数值上。PHUI-Mine和HUC-Prune消耗的内存均远远少于Two-Phase，而PHUI-Mine消耗的内存略少于HUC-Prune。

6 结束语

为提高高效用项集挖掘算法适应大规模数据的能力，提出了一种高效用项集并行挖掘算法PHUI-Mine。算法通过引入DHUI-树结构，实现了在建树的同时挖掘高效用项集，从而提高了算法的挖掘效率，降低了算法的存储开销。

[1] Agrawal R, Srikant R.Fast algorithms for mining association rules [C]∥Proc of the 20th International Conference on Very Large Data Bases (VLDB’94), 1994:487-499.

[2] Zhang Su-qi, Liang Zhi-gang, Hu Li-juan, et al. Research and application of improved multidimensional association rule mining algorithms [J]. Computer Engineering &Science,2012,34(9):174-179. (in Chinese)

[3] Yao H,Hamilton H J, Butz C J. A foundational approach to mining itemset utilities from databases [C]∥Proc of the 4th SIAM International Conference on Data Mining (SDM’04), 2004:482-486.

[4] Liu Y,Liao W-K,Choudhary A N. A two-phase algorithm for fast discovery of high utility itemsets [C]∥Proc of the 9th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining (PAKDD’05), 2005:689-695.

[5] Li Y-C,Yeh J-S,Chang C-C. Isolated items discarding strategy for discovering high utility itemsets [J]. Data & Knowledge Engineering, 2008, 64(1):198-217.

[6] Lan G-C,Hong T-P,Tseng V S.A projection-based approach for discovering high average-utility itemsets [J]. Journal of Information Science and Engineering, 2012, 28(1):193-209.

[7] Liu J,Wang K, Fung B C M. Direct discovery of high utility itemsets without candidate generation [C]∥Proc of the 12th IEEE International Conference on Data Mining (ICDM’12),2012:984-989.

[8] Song W,Liu Y,Li J H.Vertical mining for high utility itemsets [C]∥Proc of the 2012 IEEE International Conference on Granular Computing (GrC’12), 2012:512-517.

[9] Liu M,Qu J-F.Mining high utility itemsets without candidate generation [C]∥Proc of the 21st ACM International Conference on Information and Knowledge Management (CIKM’12),2012:55-64.

[10] Ahmed C F,Tanbeer S K,Jeong B-S,et al. HUC-Prune:An efficient candidate pruning technique to mine high utility patterns [J]. Applied Intelligence, 2011, 34(2):181-198.

[11] Feng L,Wang L,Jin B.UT-Tree:Efficient mining of high utility itemsets from data streams [J]. Intelligent Data Analysis, 2013, 17(4):585-602.

[12] Han J,Pei J,Yin Y,et al.Mining frequent patterns without candidate generation:A frequent-pattern tree approach [J]. Data Mining and Knowledge Discovery, 2004, 8(1):53-87.

[13] Shie B-E,Hsiao H-F,Tseng V S.Efficient algorithms for discovering high utility user behavior patterns in mobile commerce environments [J]. Knowledge and Information Systems, 2013,37(2):363-387.

[14] Tseng V S,Shie B-E, Wu C-W, et al. Efficient algorithms for mining high utility itemsets from transactional databases [J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(8):1772-1786.

[15] Cong S,Han J,Padua D A. Parallel mining of closed sequential patterns [C]∥ Proc of the 11th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’05), 2005:562-567.

[16] Wang Yong-heng,Yang Shu-qiang,Jia Yan.An efficient method for the parallel mining of frequent itemsets in very

large text databases [J]. Computer Engineering &Science,2007,29(9):110-113. (in Chinese)

附中文参考文献：

[2] 张素琪，梁志刚，胡利娟,等.改进的多维关联规则算法研究及应用[J].计算机工程与科学,2012,34(9):174-179.

[16] 王永恒,杨树强,贾焰.海量文本数据库中的高效并行频繁项集挖掘方法[J].计算机工程与科学,2007,29(9):110-113.

SONG Wei,born in 1980,PhD,associate professor,CCF member(E200019725S)，his research interest includes data mining.

吉红蕾(1985-),女，河北深州人，硕士生，研究方向为数据挖掘。E-mail:jihonglei1024@163.com

JI Hong-lei,born in 1985,MS candidate,her research interest includes data mining.

李晋宏(1965-),男，山西太原人，博士，教授，研究方向为数据挖掘和智能系统。E-mail:ljh@ncut.edu.cn

LI Jin-hong,born in 1965,PhD,professor,his research interests include data mining, and intelligent system.

A parallel algorithm for mining high utility itemsets

SONG Wei，JI Hong-lei，LI Jin-hong

(College of Computer,North China University of Technology,Beijing 100144,China)

Mining high utility itemsets is becoming a hot research topic in data mining owing to its ability to reflect users’preferences and make up for the shortcoming of measuring itemsets only by support degree.To meet the needs of larger data size,a parallel algorithm,called Parallel High Utility Itemset Mine (PHUI-Mine ),for mining high utility itemsets is proposed.Firstly,a tree structure,called DHUI-tree, is introduced to capture the information of high utility itemsets. Meanwhile, the DHUI-tree construction method is described,and the dynamic pruning strategy of DHUI-tree is discussed.Then, the parallel algorithm is presented. Experimental results show that PHUI-Mine algorithm is efficient and has low storage cost.

data mining;high utility itemset;parallel algorithm;DHUI-tree

1007-130X(2015)03-0422-07

2013-10-10;

2014-01-09基金项目：国家自然科学基金资助项目(61105045,51075423)；北京市属市管高等学校人才强教计划资助项目(PHR201108057)；北方工业大学科研人才提升计划资助项目(CCXZ201303)

TP311

A

10.3969/j.issn.1007-130X.2015.03.002

宋威(1980-),男，辽宁抚顺人，博士，副教授，CCF会员(E200019725S)，研究方向为数据挖掘。E-mail:songwei@ncut.edu.cn

通信地址：100144 北京市北方工业大学计算机学院

Address:College of Computer,North China University of Technology,Beijing 100144,P.R.China