多阶灰色支持向量机集成预测模型研究*

周华平，李敬兆

(安徽理工大学计算机科学与工程学院，安徽 淮南 232001)

多阶灰色支持向量机集成预测模型研究*

周华平，李敬兆

(安徽理工大学计算机科学与工程学院，安徽 淮南 232001)

对灰色预测模型GM(1,1)和支持向量机SVM预测模型进行分析，提出了多阶灰色支持向量机集成预测模型Dm_GM(1,1)-SVM。通过多阶缓冲算子改进灰色预测模型的预测精度，对最终预测值的各个相关指标进行预测；同时，采用粒子群优化算法对支持向量机模型进行径向基核参数和惩罚参数寻优，得到最佳参数对(c,g)，从而确定支持向量机的最佳回归模型；最后将各指标预测值作为支持向量机模型的输入，依据预测模型和预测模型的输入值求得预测结果。实验实例表明，多阶灰色支持向量机集成模型和传统的预测模型相比，在本例中预测精度更高，说明多阶灰色预测模型和支持向量机模型相结合在解决实际预测问题中具有实用价值。

多阶灰色预测模型；支持向量机；集成预测；缓冲算子；粒子群优化算法

1 引言

目前常用的预测理论有多元线性(非线性)回归预测[1]、趋势预测[2]、马尔可夫预测[3]、灰色预测[4]等，虽然预测方法颇多，但每种方法都是从不同的角度来预测，各有不同的适用范围。在针对某一种具体应用背景下方法的选择变得非常困难，容易造成较大的预测误差。针对此种情况，Bates J M和Granger C W J于1969 年首次在他的论文中提出了一种崭新的预测方法—组合预测[5～8]。组合预测方法的目的就是为了降低单个预测模型的预测误差，通过一种最优组合，提高预测的精度。但是，组合预测模型中，单个预测模型的权重问题很难解决，对于非线性、高维的系统预测，容易出现预测精度反而不如单一预测模型，所以这种组合预测模型在具体应用中凸显很大的局限性。另一方面，这些预测方法都是针对同一指标的历史观测值，实际应用中，预测值往往跟很多客观因素密切相关，是各种相关因素共同作用的结果，预测时应该考虑预测量受客观因素影响的程度。

支持向量机SVM(Support Vector Machine)早在20世纪末由Vapnik V N[9,10]等人研究并迅速发展起来，具有完备的理论基础。支持向量机成功应用于解决预测问题的研究。文献[11]采用支持向量机对地下洞室的长期岩爆进行分类，选用和岩爆最相关的岩石的最大深度、岩石的最大切向应力、岩石单轴抗压强度等参数作为支持向量机的输入向量。文献[12]选用太阳套、相关湿度和风速作为预测模型的输入向量，将支持向量机预测模型应用于太阳能功率短期预测。文献[13]基于1991至2010年的地下水深度、灌溉水量和蒸发量等数据基础，采用支持向量机模型对土壤电导率值进行动态预测。文献[14]采用支持向量机模型对海面温度进行预测。文献[15]采用支持向量机对空气质量参数进行预测。文献[16]采用模糊c-均值聚类算法、支持向量机模型和最小二乘法相结合对燃煤锅炉NOx排放量进行预测。文献[17]提出多级支持向量机模型并应用在慢性疾病患者的临床电荷分布预测中。文献[18]将最小二乘和支持向量机结合预测空气质量中CO的浓度。文献[19]采用偏最小二乘法和支持向量机方法结合构造线性和非线性模型，对血液流入大脑的分配行为的定量构效关系进行预测。

以上这些研究中，支持向量机的输入值要么是基于一维时间序列的单一历史值，要么是和预测值相关的多个影响因素的多维矩阵，但不管是模型的建立阶段还是预测阶段，都是基于输入矩阵已知或可以测量的情况。实际应用中，预测值往往跟多个客观因素密切相关，是各种相关因素共同作用的结果，所以本文不讨论基于时间序列的输入。在实际应用中，在采用支持向量机进行预测时，对于未来短期内的输入矩阵未知的情况下如何预测？本文采用多阶灰色预测模型和支持向量机预测模型相结合，组合成一种新型的预测模型，简称Dm_GM(1,1)-SVM，它不同于传统的组合预测模型，组合预测模型是每种模型分别对预测结果进行预测，然后通过一定的计算方法在分别预测结果的基础上得到一个最终预测结果。本文提出的新型预测模型是两种预测模型分别完成两类不同的预测，首先，利用多阶灰色预测模型预测未来样本输入矩阵的值，然后将该值作为支持向量机的输入，最终预测得到预测值——即系统最终的输出。这两种不同的预测之间没有时间先后关系，可以并行处理。

2 支持向量机

支持向量机通过构造最优分类超平面，将训练集中的点尽可能远地分开。如果训练集中的点线性不可分，将训练集中的点从二维空间映射到高维空间，同样将非线性问题转化为线性问题。设T={(x1,y1),…,(xl,yl)}∈(x×y)l为样本集，其中，xi∈x=Rn,yi∈y={-1,+1},i=1,…,l；最优分类超平面的求解函数为：

s.t.yi[(w·xi)+b]≥1,i=1,…,l

(1)

最优解w*和b*根据式(1)求出后,决策函数的形式为：

f(x)=sgn[(w*·x)+b*]

(2)

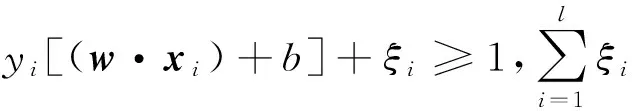
(3)

(4)

(5)

原始问题的求解就转换为它的对偶形式的解：

(6)

这是一个凸二次规划问题，求解式(6)，得到决策方程：

(7)

以上是线性可分或近似线性可分的情况，如果是线性不可分的，需引入满足Mercer条件的核函数将其转化为在高维空间求解线性问题。核函数的构造方法有多种，其中径向基核函数因其良好的性能应用较多[12～14]，本文也采用径向基核函数，引入核函数后的决策函数为:

(8)

3 多阶灰色模型Dm_GM(1,1)

灰色系统[20]GM(Grey Model)在信息量少的前提下研究小样本、贫信息等不确定性问题，认为任何随机过程都是在一定幅值范围和一定时区范围变化的灰色量，通过对部分已知少量数据的分析，找出有价值的信息，从而挖掘出系统本身固有的规律性，这种有规律性的数据必定能为未来短期内系统的发展趋势预测提供依据。灰色预测也正是基于这样的思想提出来的一种预测理论。灰色序列生成正是一种使原始数据能够体现系统变化规律的数据生成技术。从凌乱的原始数据样本中整理、挖掘出有一定变化规律、可研究的数据序列。对于冲击扰动系统预测，即系统本身受外部环境影响较大，数据是无规律、随时可能发生变化的，灰色模型预测将失去它原来的预测效果。缓冲算子[21]是解决扰动系统的有效方法之一。煤矿系统是一个复杂的灰系统，煤矿事故的发生更是动态多变、无章可循。本文的实例验证数据是预测煤矿百万吨死亡率，而煤矿百万吨死亡率跟多种客观因素密切相关，本文抽取了最相关的四个指标作为煤矿百万吨死亡率预测时的数据基础，同时也作为支持向量机的输入向量，从而预测出煤矿百万吨死亡率。而四个指标的值也是未知的，本文采用灰色模型先预测出四个指标的值。四个指标的原始数据来自于煤矿这一动态变化的系统中，数据本身缺少规律性，本文用弱化缓冲算子来对原始的受干扰的数据加以校正，但由于缓冲算子作用于原始数据序列时，必须满足不定点定理，所以原始数据序列经弱化缓冲算子作用后数据序列的增长速度减缓；相反，对于单调递减数据序列，经弱化缓冲算子作用后的数据序列的递减速度也减缓。所以，当原始数据序列变化幅度较大时，利用弱化缓冲算子会使数据序列变得平缓，增强了原始数据序列的规律性和原始数据序列的光滑度，更加适合灰色预测理论。缓冲算子对原始数据序列作用一次，记为XD，对原始数据序列作用多次分别记为：XDm,m=1,2,…,n，根据实际情况设置m值的大小，最后对预测数据进行还原。理论依据如下：

设原始数据序列:

(9)

(10)

令:

XD2=XDD=(x(1)d2,x(2)d2,…,x(n)d2)

(11)

其中，

…+x(n)d],k=1,2,…,n

(12)

对一阶缓冲算子生成的新序列再进行1-AGO，得到X′(1):

(13)

检验生成序列X′(1)的光滑度：

(14)

X′(1)经紧邻均值后为：

(15)

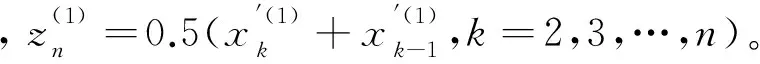
X′(1)微分得：

(16)

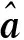
其中，

(17)

最终预测模型为：

t=1,2,…,n

(18)

4 多阶灰色支持向量机模型Dm_GM(1,1)-SVM

随着井工煤矿开采深度的增加，开采难度和开采风险进一步加剧，近年来，国家及相关单位也制定了相应的政策，煤矿安全有所好转，但煤矿安全事故仍然很严峻。从2004年起，国家高度重视煤矿安全生产，为了对煤矿定量检查和监督考核，对煤矿安全事故层层控制，国家安全生产监督管理总局(安监总局)颁布各项考核指标。从2006年起，安监总局提出构建安全生产指标体系平台，在原来指标体系的基础上，构建更合理、科学的考核指标。科学的分解算法也是构建安全控制考核指标的核心和关键所在。在这些下达的考核指标中，包括煤矿百万吨死亡率。在考核指标下达之前，如何较科学、合理地预测这一指标的值就变得至关重要。传统的方法是取前几年的平均值，这样的计算方法并没有考虑当前及将来各种因素对煤矿百万吨死亡率的影响。考虑到上述原因，提出了多阶灰色支持向量机预测模型，预测的流程如图1所示。

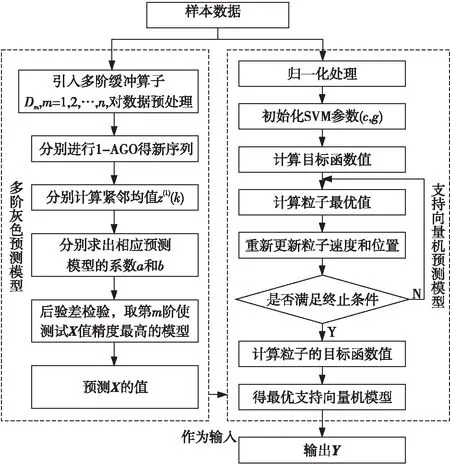
Figure 1 Forecasting process of multi-stage gray support vector machine

利用多阶灰色支持向量机模型预测时总体分为两个部分：支持向量机输入值的预测和最终结果的预测，样本数据分为输入向量X和输出向量Y。

其中，m代表样本数量，n代表和Y相关的影响因素的个数。即由输入(xi1,xi2,…,xin) 可以确定yi的值，i=1,2，…，m。本文讨论的问题就是在输入值(xi1,xi2,…,xin) 未知的情况下，如何根据前i-1个输入样本的值预测(xi1,xi2,…,xin)，然后将其作为支持向量机模型的输入值，最终预测出yi的值。预测过程如图1所示，预测步骤如下：

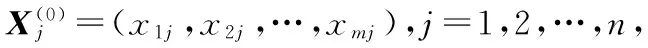
步骤5 根据后验差检验，通过测试样本分别用D1_GM(1,1)、D2_GM(1,1)、…、Dt_GM(1,1)这t个预测模型分别进行验证，取第m阶使测试样本值精度最高的模型Dm_GM(1,1)预测未知样本X的值。

步骤6 对原始数据样本进行归一化操作。

步骤7 利用粒子群算法对支持向量机模型进行参数寻优，首先初始化支持向量机参数对(c，g)。

步骤8 计算目标函数值。

步骤11 依据目标函数，判断此时粒子是否满足要求，如果是，取这时的最优参数(c,g)的值作为支持向量机的模型参数，否则算法继续迭代。

步骤12 将步骤6中的X的预测值作为支持向量机模型的输入，从而最终预测出Y的值。

5 实验仿真结果

本文数据选取以我国各产煤省(区)煤矿百万吨死亡率为预测值，选取综合机械化采煤率(%)、机械化掘进率(%)、采煤机械化率(%)和原煤全员效率(t/工)四个指标作为煤矿百万吨死亡率的相关因素。选取了全国各产煤省(区)的2004年～2012年的样本数据，包括安徽、河南、山西、贵州等21个省(区)的200多个样本数据。从中随机选取100个样本数据作为训练样本，从剩余的样本中再随机选取10个作为测试样本。最后利用建立好的模型对包括2011年的未来两年的煤矿百万吨死亡率进行预测。

5.1 基于Dm-GM(1，1)模型的各指标预测

2004年到2012年的每个省(区)的每个指标为一数据序列，利用Dm(m=1,2,…,10)对样本数据中的四个指标值作用后，分别得数据序列XD1，XD2，…,XD10。通过训练样本建立模型，确定最佳的m值。训练样本建立的预测模型的平均残差、P值和C值[20]如表1所示。

从表1中得出如下分析：首先对于原煤全员效率指标，缓冲算子Dm在m值取不同时，平均残差、P值和C值均在发生变化，均没有规律性，但m=4时，发现平均残差为0.001,达到本组最小值，P值为94%也为本组最大值，C为0.033也为本组最小值，所以m的值就取4。此时各项参数达到最优，模型也最优。同理，机械化采煤率的多阶灰色预测模型、采煤机械化率的多阶灰色预测模型和原煤全员效率的m分别为2、1和10。这样煤矿百万吨死亡率的四个指标的预测模型就确定了。下面通过测试样本分别对模型进行检验，结果如表2所示。

从表2中可以看出，利用训练好的Dm-GM(1,1)模型对煤矿百万吨死亡率的四个指标测试时，四个指标的平均残差分别为0.036、0.06、0.033和0.056，平均精度分别为88%、84%、88%和83%，方差比分别为0.081、0.261、0.078和0.198，预测精度基本上能达到80%以上，模型预测精度较高，所以Dm-GM(1,1)预测模型在煤矿百万吨死亡率各指标的预测中是可行并有效的。

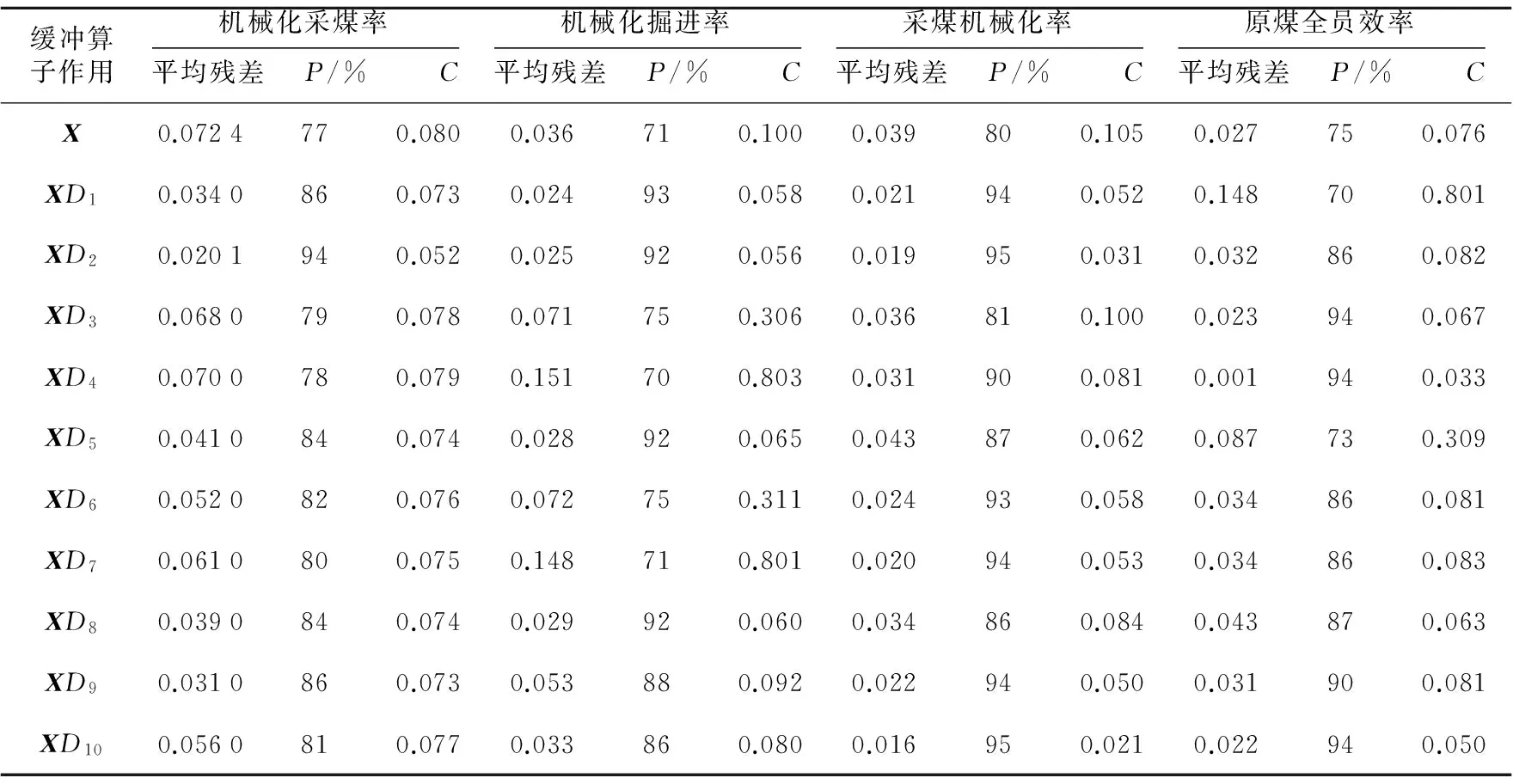
Table 1 Establishment of the value of each index m

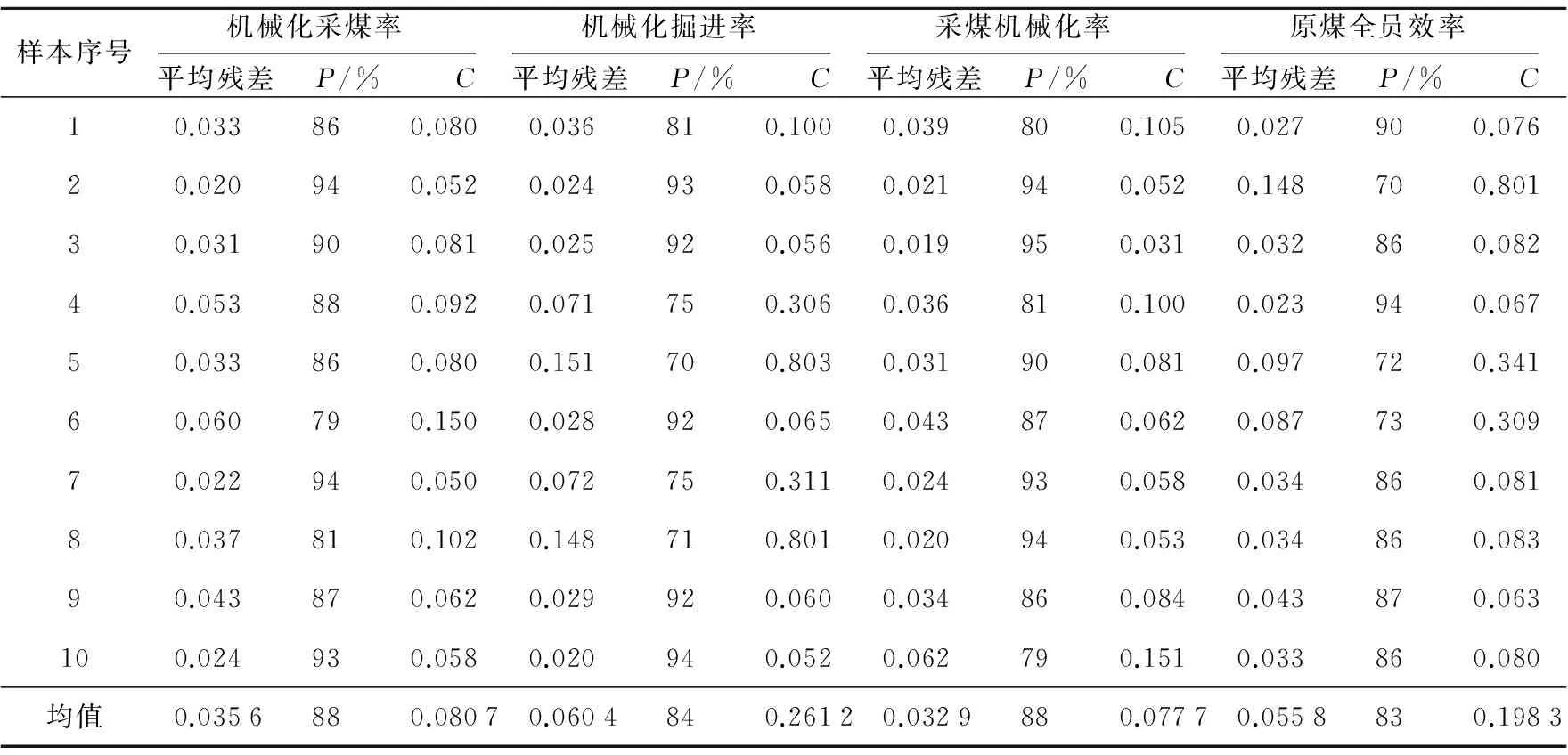
Table 2 Model checking

5.2 支持向量机预测模型的建立

煤矿百万吨死亡率支持向量机预测模型的训练和测试采用LIBSVM工具。支持向量机模型的选取主要是核参数和惩罚参数的选取，核函数采用常用的径向基核函数，利用粒子群算法(PSO)进行参数选取，采用交叉验证方法，适应度函数为煤矿百万吨死亡率的均方误差。图2为利用PSO选取参数的过程，初始参数设置c1为1.5,c2为1.7，终止代数为200，种群数量pop为20。PSO寻参算法和网格算法(GS)、遗传算法(GA)算法的搜索时间和均方根误差比较如表3所示。通过表3的比较可知，粒子群算法在本例子中均方根误差最小，更快地收敛于最优解，本模型就采用PSO的最优参数c为45.214、g为0.004作为支持向量机模型的最佳参数。

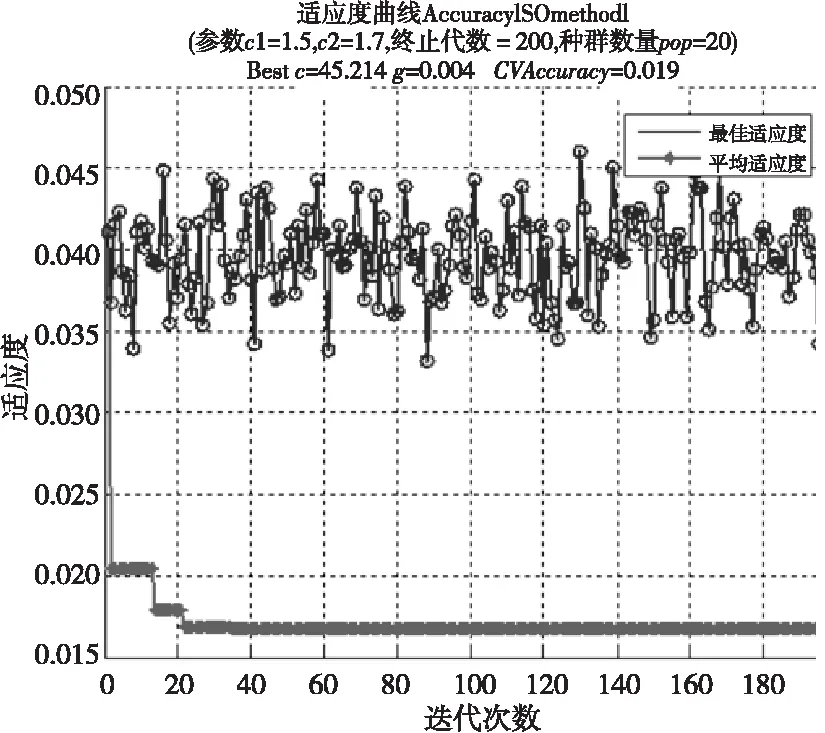
Figure 2 Fitness (accuracy) curve with PSOfinding the best parameters

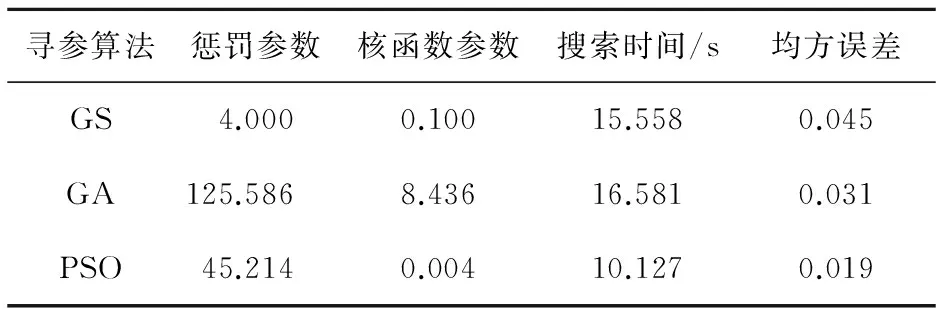
Table 3 Predicted results

选用训练好的支持向量机模型对训练样本预测时的训练样本数据的平均绝对误差是0.077 806，平方相关系数为0.959 8，均方误差是0.007 2。为了对支持向量机模型进行验证，选用30个测试样本，分为三组，预测结果如表4和图3所示，测试样本原始数据的平均相对误差是0.067，最大相对误差0.548，最小相对误差0.000 36。从测试样本预测结果看，支持向量机模型误差较小，预测有效。

5.3 方法对比

选用2012年21个省(区)的煤矿百万吨死亡率样本数据，分别利用本文提出的多阶灰色支持向量机预测模型Dm_GM(1,1)-SVM、GM(1,1)和BP神经网络组合预测模型进行预测，预测结果如表5所示，预测误差如图4所示。表5中，Dm_GM(1,1)-SVM预测的平均相对误差为5.64%，最大预测误差为9.88%，均方误差为4.73%；GM(1,1)模型进行预测的平均相对误差为25.48%，最大预测误差为14.27%，BP神经网络模型预测的平均相对误差为14.57%，最大预测误差为13.54%，均方误差为17.57。通过图4也能直观地看出Dm_GM(1,1)-SVM预测模型的预测误差最小，最接近0坐标轴，通过对三种预测模型的预测结果比较分析，Dm_GM(1,1)-SVM预测模型精度最高。

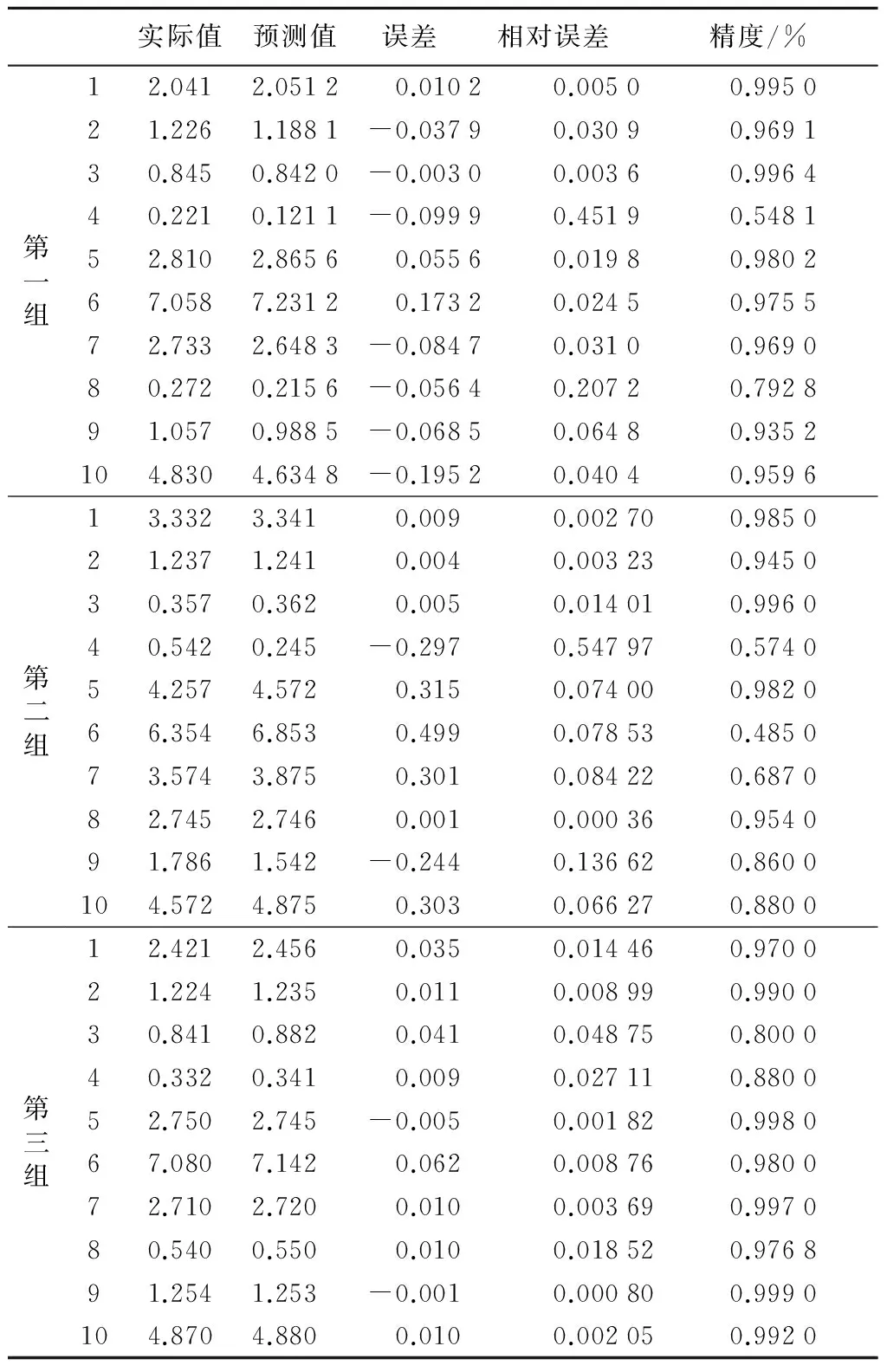
Table 4 Prediction error of test samples

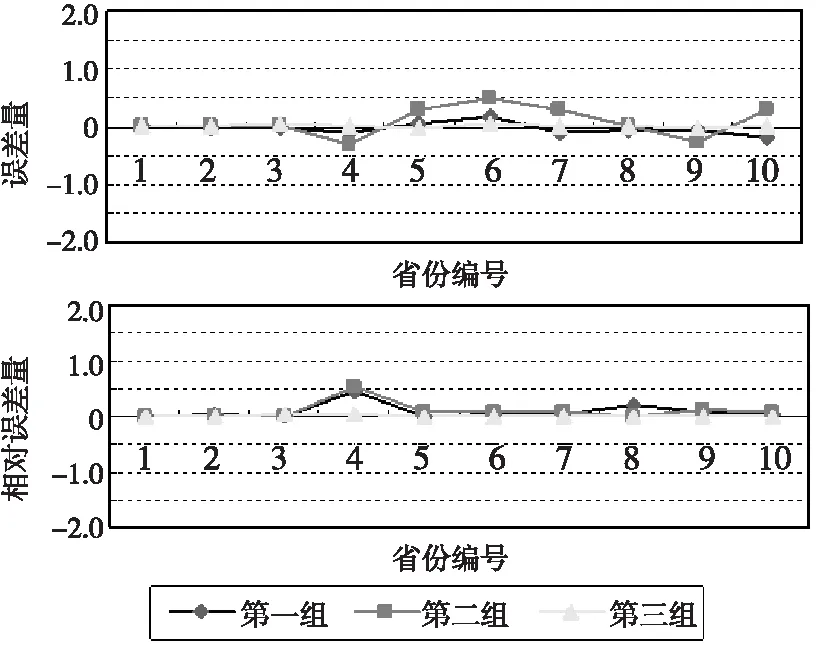
Figure 3 Prediction error curves of test samples

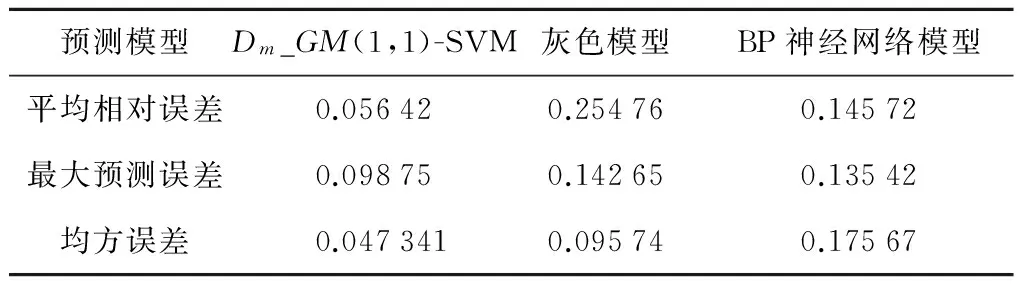
Table 5 Contrast of error values

Figure 4 Contrast curves of error values

5.4 2013～2014两年煤矿百万吨死亡率Dm_GM(1，1)-SVM预测

采用前面建立好的Dm-GM(1，1)-SVM预测模型，按照图1的预测流程，得到2013～2014两年煤矿百万吨死亡率的值，预测结果如表6所示。

Table 6 Predictive values of DRPMTC in the next two years after 2012

6 结束语

针对单一预测模型预测时的局限性，提出多阶灰色预测模型和支持向量机并行集成预测模型。采用Dm_GM(1,1)模型预测支持向量机模型的各影响因子，同时，采用粒子群优化算法对支持向量机模型进行径向基核参数和惩罚参数寻优，得到最佳参数对(c,g)的值，从而确定支持向量机的最佳模型；最后将各指标值作为支持向量机模型的输入，进行预测。利用多级灰色预测模型对各指标值的预测和支持向量机模型的训练、确立可并行。实例表明，和传统单一的预测模型相比，Dm_GM(1,1)-SVM模型具有最小的平均相对误差、预测误差和均方误差，比单一预测模型的预测精度更高，从而说明本文提出的多阶灰色支持向量机并行集成预测模型Dm_GM(1,1)-SVM是有效并可行的。

[1] Schumann S,Nolte L P,Zheng Guo-yan.Comparison of partial least squares regression and principal component regression for pelvic shape prediction[J]. Journal of Biomechanics,2013,46(1):197-205.

[2] Wen Xiang-xi,Meng Xiang-ru,Ma Zhi-qiang,et al. The chaotic analysis and trend prediction on small-time scale network traffic[J]. Acta Electronica Sinica,2012,40(8):1509-1616.(in Chinese)

[3] Cifter A.Forecasting electricity price volatility with the Markov-switching.GARCH model:Evidence from the Nordic electric power market[J].Electric Power Systems Research,2013,102:61-67.

[4] Xiang Chang-sheng, Zhang Lin-feng. Grain yield prediction model based on grey theory and Markov[J]. Computer Science, 2013,40(2):245-248.(in Chinese)

[5] Bates J M,Granger C W J. Combination of forecasts[J].Operations Research Quarterly，1969，20(4):451-468.

[6] Bischoff C W. The combination of macroeconomic forecasts[J]. Journal of Forecasting, 1989,8(3):293-314.

[7] Bunn D W. Forecasting with more than one model[J]. Journal of Forecasting, 1989,8(3):161-166.

[8] Shen Shu-jie,Li Gang,Song Hai-yan.Combination forecasts of international tourism demand [J].Annals of Tourism Research, 2011,38(1):72-89.

[9] Vapanik V N,Chervonenkis A. Ordered risk minimization[J].Automation and Remote Control,1974,35:1226-1235.

[10] Vapnik V N. Estimation of dependences based on empiricaldata[M]. Berlin:Springer-Verlag, 1982.

[11] Zhou Jian, Li Xi-bing, Shi Xiu-zhi. Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines[J]. Safety Science,2012,50(4):629-644.

[12] Zeng Jian-wu,Qiao Wei.Short-term solar power prediction using a support vector machine[J]. Renewable Energy,2013,52:118-127.

[13] Guan Xiao-yan,Wang Shao-li, Gao Zhan-yi, et al.Dynamic prediction of soil salinization in an irrigation district based on the support vector machine[J]. Mathematical and Computer Modelling, 2013,58(3-4):719-724.

[14] Lins I D,Araujo M,das Chagas Moura M, et al. Prediction of sea surface temperature in the tropical Atlantic by support vector machines[J].Journal of Computational Statistics & Data Analysis,2013,61(5):187-198.

[15] Tan Guo-hua,Yan Jian-zhuo,Gao Chen, et al.Prediction of water quality time series data based on least squares support vector machine[J]. Procedia Engineering,2012,31:1194-1199.

[16] Lv You, Liu Ji-zhen, Yang Ting-ting, et al. A novel least

squares support vector machine ensemble model for NOx emission prediction of a coal-fired boiler[J]. Energy,2013,55(C):319-329.

[17] Wei Zhong, Chow R, He Jie-yue. Clinical charge profiles prediction for patients diagnosed with chronic diseases using multi-level support vector machine[J]. Expert Systems with Applications,2012,39(1):1474-1483.

[18] Yeganeh B, Shafie Pour Motlagh M, Rashidi Y, et al. Prediction of CO concentrations based on a hybrid partial least square and support vector machine model[J]. Atmospheric Environment,2012,55(8):357-365.

[19] Golmohammadi H,Dashtbozorgi Z,William E,et al.Quantitative structure activity relationship prediction of blood-to-brain partitioning behavior using support vector machine[J]. European Journal of Pharmaceutical Sciences,2012,47(2):421-429.

[20] Liu Si-feng,Xie Nai-ming. Grey system theory and its applications[M].4th edition. Beijing:Science Press, 2008.(in Chinese)

[21] Luo Dan. Study on the properties of buffer operators and the methods of their construction[J]. Journal of Southwest University(Natural Science Edition), 2012,34(3):36-40.(in Chinese)

附中文参考文献：

[2] 温祥西, 孟相如, 马志强, 等.小时间尺度网络流量混沌性分析及趋势预测[J].电子学报,2012,40(8):1609-161.

[4] 向昌盛,张林峰.灰色理论和马尔可夫相融合的粮食产量预测模型[J].计算机科学,2013,40(2):245-248.

[20] 刘思峰，谢乃明．灰色系统理论及其应用[M]．第4版．北京：科学出版社,2008.

[21] 罗丹.关于缓冲算子的性质及其构造方法的研究[J].西南大学学报(自然科学版)，2012,34(3):36-40.

ZHOU Hua-ping,born in 1979,PhD,associate professor,her research interest includes machine learning.

李敬兆(1963-),男，安徽淮南人，博士，教授，研究方向为机器学习。E-mail:jzhli@aust.edu.cn

LI Jing-zhao,born in 1963,PhD,professor,his research interest includes machine learning.

An integrated prediction model using multi-stage gray model and support vector machine

ZHOU Hua-ping，LI Jing-zhao

(Faculty of Computer Science & Engineering,Anhui University of Science and Technology,Huainan 232001,China)

A multi-stage gray support vector machine ensemble prediction model (Dm_GM(1,1)-SVM) is presented by analyzing the gray modelGM(1,1) and the support vector machine model (SVM).The prediction accuracy of gray model is improved through multi-stage buffer operators to predict various relevant indicators.Meanwhile, the particle swarm optimization algorithm is used to find the optimal parameters of the support vector machine model, which include RBF kernel parameters and penalty parameters and the optimal pair is (c,g).Thus,the optimal support vector machine regression model is determined. Finally the final output value is predicted by inputting the predictive value of each indicator to support the vector machine model.The results show thatDm_GM(1,1)-SVM has a higher prediction accuracy compared with the gray prediction model and the BP neural network prediction model in this case,and that multi-stage gray forecasting model combined with support vector machine model has a practical value in solving practical prediction problems.

multi-stage gray prediction model;support vector machine;integrated forecasting;buffer operator;particle swarm optimization

1007-130X(2015)03-0539-08

2013-09-25;

2014-01-02基金项目：国家自然科学基金资助项目(51174257);国家973计划资助项目(2010CB732002);安徽理工大学中青年骨干教师

TP391

A

10.3969/j.issn.1007-130X.2015.03.022

周华平(1979-),女，河南唐河人，博士，副教授，研究方向为机器学习。E-mail:hpzhou@aust.edu.cn

通信地址：232001 安徽省淮南市安徽理工大学计算机科学与工程学院

Address:Faculty of Computer Science & Engineering,Anhui University of Science and Technology,Huainan 232001,Anhui,P.R.China