(η,α)-互模拟的分层及判定算法*

张晋津，张 严，朱朝晖

(1.南京审计学院工学院，江苏 南京 211815;2.南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

(η,α)-互模拟的分层及判定算法*

张晋津1，张 严2，朱朝晖2

(1.南京审计学院工学院，江苏 南京 211815;2.南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

分层刻画是传统的互模拟概念研究中的一个重要内容，它为一些互模拟判定算法提供了理论基石。(η,α)-互模拟是一种带折扣的近似互模拟概念，其定义蕴涵着一种折扣思想：在比较系统差异时，越晚出现的差异越不重要。为(η,α)-互模拟建立分层刻画，将清晰地揭示这种折扣思想。此外，由于(η,α)-互模拟一般不是等价关系，所以传统的互模拟判定算法中常用的最粗划分方法不适用于(η,α)-互模拟的判定，基于(η,α)-互模拟的分层刻画给出一种该互模拟的判定算法。还提供一个简单的例子用于说明(η,α)-互模拟及其判定算法在描述实现与规范之间关系时的应用。

(η,α)-互模拟；分层；判定算法；折扣

1 引言

近年来，状态或动作上附加定量信息的标记转换系统LTS(Labelled Transition Systems)广泛应用于描述通信系统[1]、控制系统[2,3]及实时系统[4]等。为了刻画此类系统间的等价关系，学术界提出了许多近似等价概念，例如λ-互模拟[4]、δ-互模拟[3]、(η,α)-互模拟[5]等。这些概念在描述通信或软件的可靠性[1,6]及控制系统形式化验证与设计[2]方面发挥了重要作用。

众所周知，互模拟概念可以通过多种不同方式加以刻画，例如，可以通过模态逻辑、不动点、余代数及分层方式等给出等价的定义。其中，分层刻画是一些传统互模拟判定算法的理论基石[7]，是互模拟的一种重要刻画方式。文献[3,4]分别给出了δ-互模拟和λ-互模拟的分层刻画方式。特别地，文献[3]还基于δ-互模拟的分层刻画给出了该互模拟的判定算法。

本文将建立(η,α)-互模拟的分层刻画，并在此基础上给出该互模拟的判定算法。(η,α)-互模拟中的α∈[0,1]是一个折扣因子，其定义带有折扣思想。粗略地说，两个状态是(η,α)-互模拟的，当且仅当它们之间的差异不大于η并且它们下一刻到达的状态是(η/α,α)-互模拟的。因此，当α小于1时，(η,α)-互模拟的两个系统的状态之间允许出现的差异随着系统运行时间的增加而增大。换言之，越晚出现的差异越不重要。本文建立的(η,α)-互模拟分层刻画将更为清晰地展示这种折扣思想。

2 (η,α)-互模拟

本节将回顾(η,α)-互模拟的若干相关定义和性质，这些定义与性质均出自文献[5]。该互模拟概念的提出背景、有关性质及与相关概念的讨论参见文献[5]。在给出(η,α)-互模拟概念的定义之前，需要引入下面这个记号。

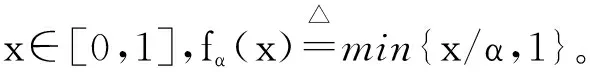
定义1 一个量化的转换系统是一个四元组R=(S,P,→,[·])，其中S是一个状态集合，P是一个有限命题集合，→⊆S×S是一个转换关系，[·]:S→(P→[0,1])是一个赋值函数。

一个量化的转换系统R=(S,P,→,[·])被称为非死锁的，当且仅当对于任意q∈S，{q′∈S:q→q′}是非空集合。一个量化的转换系统R=(S,P,→,[·])被称为有限分岔的，当且仅当对于任意q∈S,{q′∈S:q→q′}是一个有限集合。一个量化的转换系统R=(S,P,→,[·])被称为有限的，当且仅当集合S是有限的。

定义2 令α∈(0,1]并且D⊆[0,1]。我们称集合D是α-封闭的，当且仅当对于任意的x∈D，都有fα(x)∈D。

定义3 令R=(S,P,→,[·])是一个量化的转换系统并且α∈(0,1]。假设D(⊆[0,1])是α-封闭的。称一个关系序列{Rλ⊆S×S:λ∈D}是一个α-折扣互模拟序列,当且仅当对于任意的λ∈D和q，q′∈S,如果(q,q′)∈Rλ，则:

(1λ) 对于任意的r∈P，都有|[q](r)-[q′](r)|≤λ；

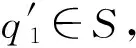
下文将{Rλ⊆S×S:λ∈D}简记为{Rλ}λ∈D。

定义4((η,α)-互模拟) 令R=(S,P,→,[·])是一个量化的转换系统，α∈(0,1]并且η∈[0,1]。一个二元关系R⊆S×S被称为是一个(η,α)-互模拟关系，当且仅当存在一个α-折扣互模拟序列{Rλ}λ∈D,使得η∈D并且Rη=R。定义(η,α)-互模拟～η,α如下：

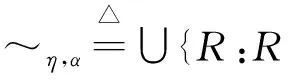
我们称两个状态q和q′是(η,α)-互模拟的,当且仅当q～η,αq′。

定理1 令R=(S,P,→,[·])是一个量化转换系统，α∈(0,1]并且η∈[0,1]。对于任意的q，q′∈S,q～η,αq′，当且仅当q和q′满足下列条件：

(iη) 对于任意的r∈P，|[q](r)-[q′](r)|≤η；

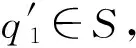
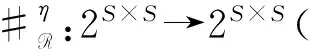
(1)对于任意的r∈P，都有|[q](r)-[q′](r)|≤η；

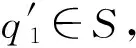
易见函数#η是一个单调函数。即，对于任意R⊆R′，#η(R)⊆#η(R′)成立。

命题1 对于任意量化转换系统R，α∈(0,1]和η∈[0,1]，～η,α=#η(～fα(η),a)。

定义6 函数σ:(0,1]×[0,1]→w-{0}定义如下：

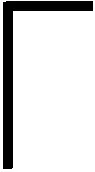
3 (η,α)-互模拟的分层

3.1 (η,α)-互模拟分层：任意框架情形

本小节将在任意量化的转换系统框架下讨论(η,α)-互模拟的分层。为此，定义如下关系序列：

假设κ=ζ+1并且η∈[0,1]。根据定义7、归纳假设和#η的单调性可得:

□

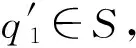
下面这个结果表明定义7可以为(η,α)-互模拟提供一种分层刻画方式。

因此，由定义4可知，只需证明下面这个结论就可完成证明:

{Rλ}λ∈[0,1]是一个α-折扣互模拟序列。

□

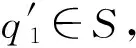
3.2 (η,α)-互模拟分层：有限分岔或非死锁情形

我们已经为任意量化的转换系统框架下的(η,α)-互模拟给出了分层的刻画方式。当量化转换系统是有限分岔或者非死锁时，可以得到更有趣的结果。下面将在此假设下讨论(η,α)-互模拟的分层。首先，与经典互模拟相关结果类似，当量化的转换系统是有限分岔时，(η,α)-互模拟的分层只需考虑ω层即可。

这个定理的证明类似于定理2，有兴趣的读者可以证明之。文献[3,8]分别为δ-近似互模拟和λ-互模拟给出了类似的分层结果。

引理2 令R是一个非死锁的量化转换系统并且α∈(0, 1]，则～1,α=S×S。

证明 因为～1,α⊆S×S显然成立，所以只需证明～1,α⊇S×S。令D={1}并且R1=S×S。显然地，D是α-封闭的。进而，容易验证{Rλ}λ∈D是一个α-折扣互模拟序列。因此，由定义4可知，S×S是一个(1,α)-互模拟关系并且～1,α⊇S×S。

□

定理4 令R是一个非死锁的量化转换系统并且α∈(0, 1)。对于任意的η∈[0,1]，都有:

□

4 折扣与(η,α)-互模拟判定算法

互模拟的判定算法是行为等价理论的一个重要研究内容[9,10]。由于(η,α)-互模拟一般不是等价关系，其判定问题不能归结为最粗划分问题(Coarsest Partition Problem)，所以不能采取传统的互模拟判定方法[11]。本文将基于定理4提出判定算法。

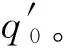
Figure 1 Stratification of (η,α)-bisimilarity (Case of non-block QTS and α<1)

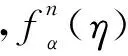
由上述论断可知，对于非死锁的量化转换系统，当α<1时，判断两个状态是否(η,α)-互模拟只需验证这两个状态的σ(α,η)步以内的后继状态是否匹配。因此，如果该量化转换系统同时也满足有限分岔性质，则两个状态是否(η,α)-互模拟是可判定的。特别地，当该量化转换系统是有限的，可以在有限步内计算得到(η,α)-互模拟的所有状态。

针对有限非死锁的量化转换系统，下面给出(η,α)-互模拟判定算法：

算法1 (η,α)-互模拟判定算法

(1)InputR=(S,P,→,[·])、η、α

(2) Computeσ(α,η)

(3) leti=1,R1=S×S

(4) whilei≤σ(α,η) do{

(4) setS1to be the domain of the relationRi

(5) for allq1∈S1do{

(6) add (q1,q1) to relationRi+1;

(7) for allq2∈S1withq1≠q2do

(8) if for anyr∈P, |[q1](r)-[q2](r)|≤η/ασ(α,η)-i+1&Match(Ri,ReachSet(q1),ReachSet(q2)) &Match(Ri,ReachSet(q2),ReachSet(q1)) /*见算法2 */

(9) add (q1,q2) to relationRi+1}

(10)i=i+1}

(11) returnRi-1

在上述算法中涉及两个函数：Match和ReachSet。ReachSet函数用于求得给定状态的后续状态集合，例如ReachSet(q)是状态q所有一步可达状态组成的集合。这个函数根据量化的转换系统直接可得，在此不再赘述。Match函数用于判断集合S1与S2中元素是否保持R关系，具体而言，如果对于S1中任意元素，均存在q2∈S2使得(q1,q2)∈R，则Match函数返回值true，否则返回false。Match函数算法如下：

算法2Match函数

Match(R,S1,S2)

(1)for allq1∈S1do{

(2) try to find an elementq2∈S2so that (q1,q2)∈R

(3) if suchq2does not exist

(4) return false}

(5)return true

根据定理4，可以验证该算法是正确的。此外，容易验证给定量化的转换系统R=(S,P,→,[·])，该算法的时间复杂度为O(|S|4)。

5 (η,α)-互模拟的应用

下面将给出一个简单的例子说明(η,α)-互模拟在实际应用中的作用。给定一个控制系统，其输入电压每100 ms可变化一次。图2a给出了一个规范，要求该控制系统的输入电压满足该规范。即，输入电压最初要求为0，在100 ms时可变化为1或0.5。若变化为1，则其后时间100*n(n>1)ms时刻保持为1或者变化为0.8，一旦变化为0.8，则之后都应保持为0.8。若100 ms时变化为0.5，则其后时间100*n(n>1)ms时刻保持为0.5或者变化为0.8或0.3，一旦变化为0.8或0.3，则之后都应保持为0.8或0.3。

由于物理设备本身存在误差，所以实际实现的系统一般不能严格满足该规范，进而需要允许一定误差存在，设定允许误差η=0.03。此外，由于系统运行初期可能不稳定，因此严格要求输入电压的误差不得超过规定值。随着系统运行时间的增加，系统逐渐稳定和适应环境，对输入电压的误差限定逐渐放宽，即误差限定可以打折扣。为此，设定折扣因子α=0.9。

Figure 2 Specification and its implementation

假设根据上述规范设计实现的一个输入电压变化系统如图2b所示。显然，当采用传统互模拟概念刻画实现与规范间满足关系时，由于图2b所示的实现与图2a所示的规范不具有互模拟关系，因此视为该实现不满足规范。事实上，由于物理设备误差的存在，实现与规范都不能保持互模拟关系。所以，当采用传统互模拟概念时，实现一般都不满足规范。因此，采用传统互模拟概念刻画实现与规范间满足关系是不恰当的。

根据上述关于规范满足条件的描述，如果实现与规范是(η,α)-互模拟的，则可认为该实现满足规范。由第4节提供的算法，容易验证图2b所示的实现与图2a所示的规范是(η,α)-互模拟的。因此，可以认为该实现满足给定规范。

6 结束语

(η,α)-互模拟是一种带折扣的近似互模拟概念。本文为其建立了分层刻画方式，清晰地展示了折扣的思想。这种分层刻画又为(η,α)-互模拟的判定算法提供了理论基石。由于(η,α)-互模拟一般不是等价关系，无法采用传统的最粗划分方法，本文基于(η,α)-互模拟的分层刻画为其提供了一种可用的判定算法。但是，该算法不是线性时间的，今后我们将进一步研究在哪些量化转换系统框架下，可以给出线性时间的(η,α)-互模拟判定算法。

[1] Ying Ming-sheng. π-calculus with noisy channels [J]. Acta Informatica, 2005, 41(9):525-593.

[2] Girard A, Pappas G. Approximate bisimulation:A bridge between computer science and control theory [J]. European Journal of Control, 2011, 17(5):568-578.

[3] Girard A, Pappas G. Approximation metrics for discrete and continuous systems [J]. IEEE Transactions on Automatic Control, 2007, 52(5):782-798.

[4] Ying Ming-sheng. Bisimulation indexes and their applications [J]. Theoretical Computer Science, 2002, 275(1-2):1-68.

[5] Zhang Jin-jin, Zhu Zhao-hui. Characterize branching distance in terms of (η,α)-bisimilarity [J]. Information and Computation, 2008, 206(8):953-965.

[6] Cao Yong-zhi.Reliability of mobile processes with noisy channels [J]. IEEE Transaction on Computers, 2012, 61(9):1217-1230.

[8] Milner R.Communication and concurrency[M]. New York:Prentice Hall, 1989.

[9] Li Zhou-jun,Chen Huo-wang.Bisimulation checking algorithms based on symbolic transition graphs [J]. Computer Engineering & Science, 2002, 24(2):34-41.(in Chinese)

[10] Xu Wen,Fang Hai, Lin Hui-min. Optimization and implementation of a bisimulation checking algorithm for the π-calculus [J]. Journal of Software, 2001, 12(2):159-166. (in Chinese)

[11] Paige R,Tarjan R E, Bonic R. A linear time solution to the single function coarsest partition problem [J]. Theoretical Computer Science, 1985, 40(1):67-84.

附中文参考文献：

[9] 李舟军，陈火旺. 基于符号迁移图的互模拟验证算法 [J]. 计算机工程与科学, 2002, 24(2):34-41.

[10] 许文，方海，林慧民. π-演算互模拟判定算法的优化和实现 [J]. 软件学报, 2001, 12(2):159-166.

ZHANG Jin-jin,born in 1981,PhD,lecturer，his research interests include formal methods, and logics in computer science.

张严(1983-),男，江苏南通人，博士生，研究方向为形式化方法和计算机科学中的逻辑学。E-mail:yanzhang_nuaa@nuaa.edu.cn

ZHANG Yan,born in 1983,PhD candidate,his research interests include formal methods, and logics in computer science.

朱朝晖(1970-),男，江苏南通人，博士，教授，研究方向为形式化方法和计算机科学中的逻辑学。E-mail:zhaohui.nuaa@gmail.com

ZHU Zhao-hui,born in 1970,PhD,professor,his research interests include formal methods, and logics in computer science.

Stratification and checking algorithm of (η,α)-bisimilarity

ZHANG Jin-jin1，ZHANG Yan2,ZHU Zhao-hui2

(1.School of Technology,Nanjing Audit University,Nanjing 211815;2.College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

The stratification of bisimilarity is an important issue in the classical research on bisimilarity. It provides a theoretical basis for some checking algorithms of bisimilarity. We establish the stratification of (η,α)-bisimilarity in this paper.(η,α)-bisimilarity is a notion of approximate bisimilarity with discount factor. It is defined with a discounted setting, which means that the difference occurring in the far away future is not as important as the difference occurring in the near future, which will be revealed in the stratification established in this paper. Moreover, since (η,α)-bisimilarity is not always an equivalence relation, the coarsest partition method used in classical checking algorithms of bisimilarity cannot be adopted to offer a checking algorithm of (η,α)-bisimilarity.Based on the stratification of (η,α)-bisimilarity, we provide a checking algorithm of this bisimilarity.We also offer a simple example to illustrate how to apply (η,α)-bisimilarity and its checking algorithm to capture the satisfaction relation between implementations and specifications.

(η,α)-bisimilarity;stratification;checking algorithm;discount

1007-130X(2015)03-0547-06

2013-11-08;

2014-01-08基金项目：国家自然科学基金资助项目(60973045,11426136);江苏省高校自然科学基金资助项目(13KJB520012)

TP302

A

10.3969/j.issn.1007-130X.2015.03.023

张晋津(1981-),男，山西曲沃人，博士，讲师，研究方向为形式化方法和计算机科学中的逻辑学。E-mail:jinjinzhang@nau.edu.cn

通信地址：211815 江苏省南京市南京审计学院工学院

Address:School of Technology,Nanjing Audit University,Nanjing 211815,Jiangsu,P.R.China