基于FPGA的Edwards曲线标量乘法实现方法*

韩炼冰,段俊红,王 松,房利国,刘 蕴

(中国电子科技集团公司第三十研究所，四川 成都 610041)

基于FPGA的Edwards曲线标量乘法实现方法*

韩炼冰,段俊红,王 松,房利国,刘 蕴

(中国电子科技集团公司第三十研究所，四川 成都 610041)

点加和倍点是标量乘法的基本运算。首先对原始的Edwards曲线计算公式进行了研究,再结合FPGA并行计算的特点，提出了一种适合FPGA快速实现的点加和倍点计算方法；其次给出了并行和串行两种标量乘法算法。最后在ALTERA的EP2AGX260 FPGA中分别对两种标量乘法进行了实现和测试。结果表明，该实现方法能达到较理想的效果。

Edwards曲线；FPGA；标量乘法；点加；倍点

0 引 言

椭圆曲线密码体制(ECC)是1985提出的。同RSA密码体制比，要达到相同安全强度，它可以使用较RSA密码更短的密钥。由于密钥短，所以工程实现的加密速度较快，并节省资源、带宽和存储空间，适于在移动通信、智能卡等系统中运用[1]，并已成为信息安全领域研究的热点。

Edwards[2]曲线是2007年提出的一种新形式的椭圆曲线，该曲线的主要优势是其上的群运算规则较简单，且倍点和点加运算具有相同的公式。文献[3]的进行一步研究表明Edwards群运算的效率及安全性优于Jacobian等其他形式的椭圆曲线[4]。

椭圆曲线标量乘法np是ECC中最耗时的运算，直接影响着ECC算法的运算效率。本文首先介绍Edwards曲线及其运算算法，再根据FPGA并行计算的特性，将原算法进行分解，设计了一种采用两个模乘法器和一个模加法器结构的快速点加实现方法，并将其用在了标量乘法的FPGA编程实现中。

1 Edwards曲线

Edwards给出的椭圆曲线表达形式为：

X2+Y2=C2(1+X2Y2)

(1)

(0,C)为曲线式(1)的零元，该形式下的曲线加法较简单，且加法法则具有完备性。Bernstein和Lange将Edwards曲线进行扩展，表达形式为[5]：

X2+Y2=C2(1+dX2Y2)

(2)

其中c,d∈k,c,d≠0，且cd4≠1,(0,1)为其零元。进一步的研究表明，任何特征值不为2的域上的椭圆曲线均可转换为该域上C=1的曲线，即式(2)简化为:

X2+Y2=1+dX2Y2

(3)

曲线式(3)的零元为(0,1)。令P1=(X1,Y1),P2=(X2,Y2)为曲线式(3)上的两个点，P3=(X3,Y3)为P1,P2两点相加的结果，则有:

(4)

对于倍点运算，即当P1=P2时，公式(4)仍然成立。Edwards曲线点加和倍点计算公式相同的这一特性对FPGA实现来说可以节省不少的资源，尤其是在域的数据很大，如256比特或者更多时。

2 标量乘法的FPGA实现

标量乘法nP的运算最终都会转化成多次点加和倍点运算来完成。通过公式(4)知道，完成一次点加或者倍点需要进行2次求逆运算，8次乘法运算，4次加法运算。通常求逆运算非常耗时，为了尽可能的减少求逆运算，采用标准射影坐标代替原来的仿射坐标，即仿射坐标下的点(x,y)在射影坐标下表示成(X,Y,Z)，两种坐标下点的对应关系为x=X/Z,y=Y/Z,Z≠0。在射影坐标系下，不需要对每次点加或者倍点后的结果求逆，只需要在运算完成后从射影坐标转换到仿射坐标时进行一次求逆运算，因而大大提高了算法实现效率。标量乘法的设计框图如图1所示：

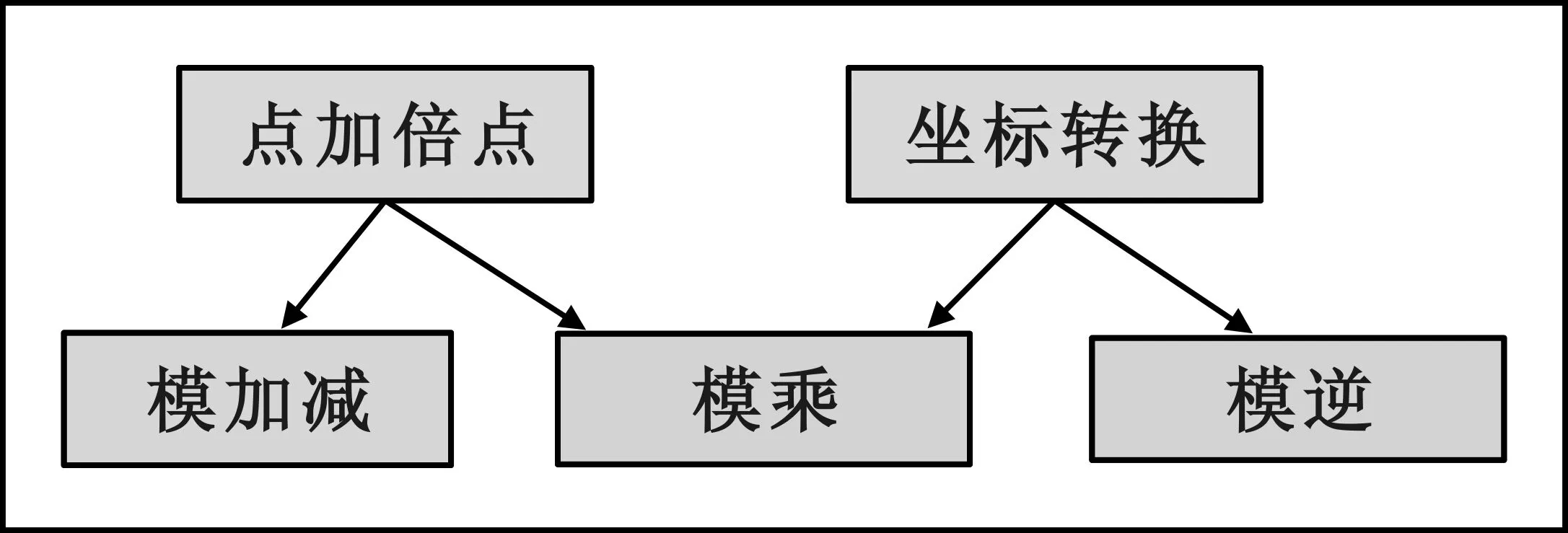
图1 标量乘法设计框图

2.1 点加倍点的FPGA实现

假定P1=(X1,Y1,Z1),P2=(X2,Y2,Z2)为射影坐标的两点，P3=(X3,Y3,Z3)为P1,P2两个点相加的结果，那么有:

FPGA实现时，采用2个模乘法器和1个模加减法器的并行结构，并定义一些寄存器存放中间结果，约7次模乘后即可完成X3,Y3,Z3的计算，实现框图如图2所示。点加的FPGA实现算法如下：

算法1：点加运算

输入：P1=(X1,Y1,Z1),P2=(X2,Y2,Z2)

输出：P3=(X3,Y3,Z3)

(1)t1=X1Y2t2=X2Y1NULL

(2)t3=Z1Z2t2=t1t2t1=t1+t2

(3)t5=X1X2t4=Y2Y1NULL

(4)t6=t3t3t2=dt2t4=t4-t5

(5)t4=t4t3t5=t1t3t1=t6-t2

(6)NULLNULLt3=t6+t2

(7)Y3=t4t3Z3=t1t3NULLt2←t5

(8)NULLX3=t1t2NULL

其中，每个步骤中的三列分别对应于图2中的模乘法器1、模乘法器2和模加减法器。t1,t2,t3,t4,t5,t6为寄存器中间结果，NULL表示当前步骤不做运算。值得注意的是：椭圆曲线运算的数据通常都是一个大数，在某些FPGA上实现时往往出现FPGA的逻辑资源使用不多，但编译却失败的情况。这种情况多因为FPGA内部数据位宽很宽，导致了局部布线资源不足。算法1的步骤7)中t2←t5表示在模乘法器运算完成后将t5的值赋给t2，不属于加法器或者乘法器的运算。这样可以减少模乘法器2的一个输入变量，对FPGA设计起到一定的优化作用。

图2 点加实现框图

2.2 模乘及模加减的FPGA实现

模乘法器采用文献[6]的快速实现方法，并将流水线级数增加了原文的一倍，从而使模乘运算的效率提高了42%。以384比特的数据为例，完成一次模乘运算的时间，从原来的96个时钟节拍减少到改进后的56个时钟节拍。

模加减法器完成两个大数的相加或相减并对结果取模，实现方法为：将大数拆分成多个64 bit段，每段数据串行相加或者相减并进行模运算。以384比特数据为例子，完成一次模加减运算需要7个时钟节拍。

2.3 坐标转换及求逆的实现

标量乘法完成后需要将射影坐标系的点(X,Y,Z)转换仿射坐标的点(x,y)，其中x=X/Z,y=Y/Z。计算x,y时，与点加倍点共用模乘法器1和模乘法器2。

求逆运算采用扩展的欧几里德算法。

2.4 标量乘法的实现

标量乘法中的通常是一个大整数。FPGA实现时将n转换成二进制形式，再逐位计算。计算时有两种方法：一是由低位向高位开始计算，称为并行计算；二是由高位向低位计算，称为串行计算。两种计算算法如下：

算法2：标量乘法并行计算

输出：Q=nP

(1)Q←0

(2)Forifrom0tok-1do

(3)Ifni=1,Q←Q+P

(4)P←2P

(5)endfor

(6)returnQ

算法3：标量乘法串行计算

输出：Q=nP

(1)Q←0

(2)Forifromk-1to0do

(3)Q=2Q

(4)Ifni=1,Q←Q+P

(5)endfor

(6)returnQ

算法2和算法3中的Q+P为点加运算，2P和2Q为倍点计算。从算法2的计算公式可以看出，该算法的优点有：一是在FPGA实现时，点加运算和倍点运算可以并行执行，能大大提高算法效率；二是算法的运算时间不依赖于n的具体比特位值，因此可以抵御SPA(简单能量攻击)等。算法2的缺点是多占用FPGA的硬件资源。算法3的优缺点恰与算法2相反，点加运算需用到倍点的运算结果，使算法只能串行计算，从而降低算法性能。同时，点加是否执行依赖于当前循环的比特位ni是否为1，因此计算时间与具体的n值有关。但算法3的优点是点加倍点共用一个模块，可以大大减少硬件资源。

2.5 实现结果

选用ALTERA公司的EP2AGX45C6FPGA平台对算法2和算法3进行了实现。表1和表2分别给出了并行和串行两种实现方式的性能和资源比较，其中，实现1对应算法2，实现2对应算法3。

表1 性能比较

表2 资源消耗比较

3 结 语

本文将原始的点加公式进行了坐标转换，将转换后的公式进行了分解，给出了适合FPGA并行计算的点加计算公式。最后给出了两个标量乘法计算公式，分别对应于FPGA的资源优先和性能优先两种实现方式，并对两种实现方式的资源和性能做了比较，有很好的实用意义。

标量乘法中的倍点运算是必不可少的，当前有关标量乘法的优化都是减少点加运算的次数(如非相邻表示(NAF)法[7],窗口法[8]等)，但由此会带来额外的资源转换开销或者存储资源开销，对于资源宝贵的FPGA而言不一定适合。目前，针对Edwards曲线FPGA实现的研究较少，如何提高标量乘法的性能且又适合FPGA实现还需更深入的研究。

[1] 金晓刚.素数域上椭圆曲线密码体制的软件实现[J].通信技术，2010,43(09):136-138. JIN Xiao-gang. Software Implementation of Elliptic Curve Cryptosystem over Prime Field[J].Communications Technology，2010,43(09): 136-138.

[2] Edwards H M.A Normal Form for Elliptic Curves[J].Bulletin of the American Mathematical Society, 2007, 44(3): 393-422.

[3] Bernstein D J，Lange T. Faster Addition and Doubling on Elliptic Curves[J].Asiacrypt,2007(10):29-50.

[4] 张宝华,殷新春,张海灵.Edwards曲线安全快速标量乘法运算算法—EDSM[J].通信学报，2008,29(10):76-81. ZHANG Bao-hua, YIN Xin-chun，ZHANG Hai-ling. EDSM: Secure and Efficient Scalar Multiplication Algorithm on Edwards Curves[J].Journal on Communications，2008,29(10):76-81.

[5] 苏贺鹏，张盛兵.基于二进制Edwards曲线的椭圆曲线加密多标量乘法结构设计与实现[J].微电子学与计算机, 2011,28(2):98-102. SU He-peng, ZHANG Shen-bing. Design and Implementation of an Architecture Multi-Scalar Multiplication for ECC based on Binary Edwards Curves[J].Microelectronics & Computer, 2011,28(2):98-102.

[6] 韩炼冰，黄锐，段俊红.基于FPGA的素域模乘快速实现方法[J].信息安全与通信保密,2013(09):76-78. HAN Lian-bing，HUANG Rui，DUAN Jun-hong. Fast Implementation Method of Prime Fields Modular Multiplication based on FPGA[J].Information Security and Communications Privacy,2013(09):76-78.

[7] 龚亮.基于GF(P)椭圆曲线加密的点乘实现方案[J].大众科技，2011(12):4-6. GONG Liang. Implementation of Point Multiplication for ECC over GF(P)[J].Popular Science,2011(12):4-6.

[8] 刘彬彬，聂意新，严烨.椭圆曲线倍点算法的比较研究[J].信息网络安全,2013(06):22-25. LIU Bin-bin, NIE Yi-xin, YAN Ye. Comparisons of Point Multiplication in Elliptic Curve Cryptography[J].Net Info Security,2013(06):22-25.

FPGA-based Implementation of Scalar Multiplication on Edwards Curve

HAN Lian-bing, DUAN Jun-hong, WANG Song, FANG Li-guo, LIU Yun

(No.30 Institute of CETC, Chengdu Sichuan 610041, China)

Point-plus and double-point operation is the basic operation of scalar multiplication. Firstly, the original formula of Edwards curve is studied, and in combination with the characteristics of FPGA parallel computing,a point-plus and double-point computing method suitable for fast implementation of FPGA is proposed,and then both parallel and serial scalar multiplication algorithms are presented, and finally, both two scalar multiplications are implemented and tested on EP2AGX260 FPGA of ALTERA. Results show that this implementation method could achieve a fairly ideal effect.

Edwards curve; FPGA; scalar multiplication; point plus; double point

10.3969/j.issn.1002-0802.2015.10.016

2015-06-01；

2015-09-14 Received date:2015-06-01；Revised date：2015-09-14

TN918.4

A

1002-0802(2015)10-1179-04

韩炼冰(1984—)，男，学士,工程师，主要研究方向为信息安全、通信安全技术;

段俊红(1984—)，男，工程师，主要研究方向为嵌入式系统、通信安全技术;

王 松(1985—),男，学士,工程师，主要研究方向为信息安全、通信安全技术;

房利国(1977—)，男，硕士，高级工程师，主要主要研究方向为信息安全、通信安全技术、计算机应用;

刘 蕴(1981—)，女，硕士，工程师，主要研究方向为信息安全。