基于CPLD的简易串行数字乘法器

茹胜华， 马 亮， 周丽君

（上海无线电设备研究所，上海200090）

0 引言

在现代可编程逻辑电路的设计中，通常采用具有乘法器单元的FPGA 完成高速、复杂的信号处理算法［1］，以较高的成本解决数字信号处理中大量乘法运算。但在对乘法运算和时序逻辑有需求但不高的场合，若采用FPGA 设计乘法器，浪费资源，增加产品成本，且难于技术加密。针对这种情况，本文采用无乘法器资源的CPLD 完成16位无符号数字乘法器的设计，它以串行、移位方式进行数据相乘运算，特别适合串行通讯。该乘法器运算步骤少，算法简单，占资源少，可封装为经典模块，供重复使用。

1 算法推理

无符号数字串行乘法可以从6位二进制乘法展开推导，归纳总结出n位的二进制乘法。

设有两个6位二进制A 和B，分别为

那么，A 与B的乘积X 可以表示

X ＝A×B ＝x11×211+x10×210+x9×29+x8×28+x7×27+x6×26+x5×25+x4×24+x3×23+x2×22+x1×21+x0×20

其中：

c1～c10为乘积X 的第1位数（x1）～第10位数（x10）的进位，从x0～x11的表达式可以总结出第k位数的通式xk。

式中：i+j＝k，i是乘数A 的下标，j是乘数B 的下标，k是乘积X 的下标；0≤i ≤k，0≤j ≤k；0≤i≤n-1，0≤j ≤n-1；0≤k ≤11，即k ≤2n-1，n是乘数和被乘数的位数，式中n＝6；

从6位的乘法的计算公式，可以归纳、总结出两个n位二进制数的乘法。假定：两个n 位二进制数分别为A（an-1an-2……a2a1a0）和B（bn-1bn-2……b2b1b0），那 么，它 们 的 乘 积X（x2n-1x2n-2x2n-3……x2x1x0）可表示为

式（4）为两个n 位无符号串行二进制数乘法的逐位运算规则，xk是乘积X 第k 位数的运算通式。

2 算法设计

依据式（4），可以将两个n 位乘法计算分为n次完成，每次计算均按照xk项进行计算，如图1所示。

图1 串行二进制乘法器算法原理

图1中，被乘数与乘数按照移位时序送入寄存器，每次移位将对“被乘数”、“乘数”和“进位”计算，形成该位“乘积”和“进位”。随着数据的串行进入，逐位求积，当信号结束时，完成乘法运算。在每一次计算完成后，对乘数、被乘数和进位寄存器进行清零，准备下一次的乘法运算。

3 基于CPLD 的乘法器的实现

根据上述算法原理，设计16位乘法器［2］，如图2所示。

图2 16位乘法器电路

图2 中，寄存器B 的Q0～Q15 的输出为QB0～QB15，寄存器A 的Q0～Q15 的输出为QA0～QA15，工作可分为以下几个阶段。

乘法器工作流程如下：

a）乘数装订，按照时序首先给寄存器B装订乘数，从寄存器B的QB0～QB15输出，可以串行装订，也可以并行装订；

b）被乘数寄存器A 清零，即QA0～QA15置“0”，本步骤可与乘数装订同时进行；

c）被乘数输入，寄存器A 按序逐位输入16位串行被乘数；

d）对寄存器A 依次进入的数据，进行逐位计算，并最终形成乘积。

在相同的时钟周期情况下，该乘法器的最快运算周期数为：乘数加载周期数、被乘数位数、乘数位数的总和，即33个时钟周期。

4 仿真及试验验证

根据图2，运用原理图方法完成乘法器设计。为验证上述算法的有效性，采用Lattice公司的ispLEVER 软件进行时序仿真［4］，结果分别如图3、4所示。

图3、4中，各信号意义如下：CLEAN 是进位寄存器清零信号，“1”有效；CLOCK A 是寄存器A（被乘数寄存器）的时钟，上升沿有效；CLOCK B是寄存器B（乘数寄存器）的时钟，上升沿有效；CLOCK C 是进位寄存器的时钟，上升沿有效；CMA 是寄存器A 的串并工作方式控制，“0”为串行状态，“1”为并行方式；CM B 是寄存器B 的串并工作方式控制，“0”为串行状态，“1”为并行方式；DATA A 是寄存器A 的串行输入数据，先低后高；DATA B 是寄存器B 的串行输入数据，先低后高；PDB0～PDB15是寄存器B 的并行输入数据，其中PDB0 为最低位，PDB15 为最高位；DOUT 为乘积输出，先低后高。

图3对第一组数据输入进行仿真，寄存器B的并行端口D0～D15 输入并行数据（PDB）为1000010101110001；在寄存器A 的Data A 端口依次输入串行数据为0001111000011101（送数次序为先低后高）。仿真结果为32 位数据为00001111101100100101101111001101，即为寄存器A、B的乘积，验证了乘法器的有效性。

图3 第一组16×16位数乘法器仿真结果

图4 第二组16×16位数乘法器仿真结果

图4对第二组数据输入进行仿真，寄存器B输 入 0001011100100000，寄 存 器 A 输 入0001111111100000。仿真结果为32 位数据为00000010111000010001110000000000，即为寄存器A、B的乘积，也验证了乘法器的有效性。

仿真结果达到预期效果后，通过CPLD 的硬件平台，完成软件的下载，模块验证结果与仿真完全一致。目前，该16位乘法器作为模块使用，经过级连扩展成64位串行乘法器，在某产品上稳定工作。该乘法器算法的实现，避免了硬件平台向FPGA 升级所造成资源和成本的浪费。

5 使用资源的估算

采用上述方法设计的乘法器所使用的资源与采用的编译软件、CPLD 器件类型、编写代码（原理图、VHDL 等）等因素相关。下面撇开这些干扰因素，对该乘法器使用的资源进行理论推算［3］。

从图1可以看出，该乘法器由与门、全加器和寄存器构成。

5.1 两输入与门数量

两输入的与门使用的总数量应等于被乘数或乘数的位数，即与门数＝n；

5.2 三输入全加器数量

全加器由本位全加器和进位全加器构成，进位全加器又分为十位全加器、千位全加器、万位全加器、…、l位全加器，l应满足2l≥n，r1为满足3r1 ≤n的最大整数。

……

综上所述，n 位乘法电路所用全加器的总数Un为：

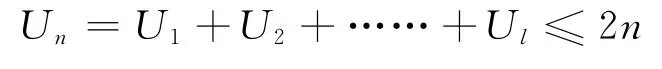
5.3 寄存器数量

寄存器分为进位寄存器、乘数寄存器和被乘数寄存器三类。进位寄存器由2p1≥n 决定，即p1≥log2n。乘数寄存器和被乘数寄存器各一个。

综合上述，乘法器所用总资源如表1所示。

上述计算分析表明，该乘法器占用较少的资源。

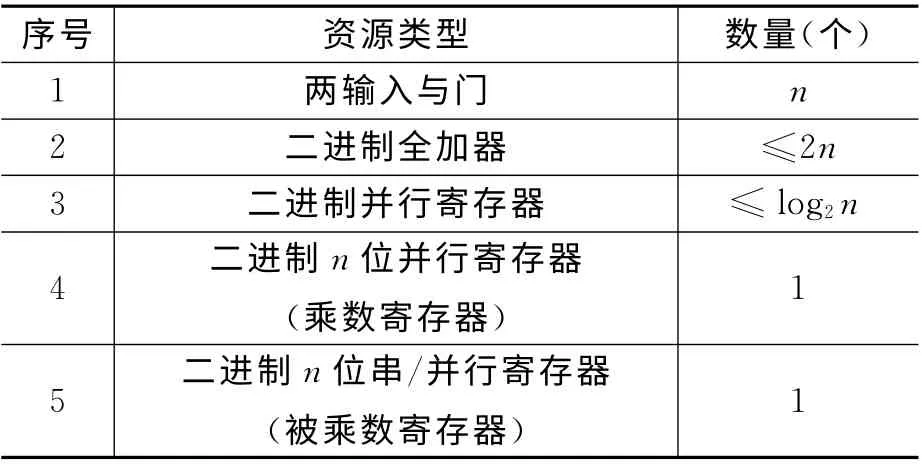
表1 乘法器所用资源汇总

6 结束语

本文针对不含有内置乘法器的CPLD，对串行乘法器的乘法机理进行详细分析后，形成算法设计和原理图设计，并进行时序仿真和试验验证，最终验证了串行无符号整数乘法器设计有效。采用该方法设计的乘法器占用较少的资源，并具有良好的扩展性，能够扩展到任意位数。在含有内置乘法器的FPGA 设计中，该设计方法可以大大扩展乘法器的可用数量，在实时性要求不高的条件下，选择低容量器件，降低成本，减少硬件资源浪费。

上述乘法器通过拓展，可应用于其它实时性要求不高的场合。比如，增加一个串行转并行的模块，就可以实现并行数据的乘法；增加符号位的异或门，可应用于有符号的运算。另外，通过对浮点数进行整数化近似后，分别进行整数相乘和指数相加的运算，可将本乘法器应用于浮点小数的近似运算，以降低成本和资源。

［1］ 王磊磊.基于CZT 的频率细化方法的FPGA 实现［J］.制导与引信，2010，31（1）：29-32.

［2］ 吴静，李树荣，等.一种基于RISC 结构单片机的数字乘法器的设计.微电子学，2004，34（5）：593-594.

［3］ 罗朝杰.数字逻辑设计基础上册［M］.北京：人民邮电出版社，1982，（9）：223-224.

［4］ 高路.基于FPGA 的DSP外部总线接口设计［J］.制导与引信，2011，32（2）：20-23.