空时自适应处理算法性能影响因素分析

张 燕， 马 亮， 陈春芳

（上海无线电设备研究所，上海200090）

0 引言

地面运动目标指示（Ground Moving Target Indication，GMTI）技术已经广泛应用于军事探测领域。空时自适应处理（Space-Time Adaptive Processing，STAP）算法是一种典型的多通道GMTI方法，因其出色的杂波抑制能力而成为慢速运动目标检测的有效方法之一［1-5］。

传统的运动目标检测方法采用单通道方式。单通道方法一般假定运动目标频谱在杂波谱之外，对回波信号进行频域滤波处理，就可以将目标频谱从地杂波谱中分离出来。所以，单通道方法一般检测不到频谱落入地杂波带内的运动目标，即难以检测相对慢速的目标。只有通过增加雷达系统空间维的信息，同时利用空间和时间二维信息才能有效抑制杂波。

地（海）杂波在角度和多普勒两维展宽，反映在空时两维平面上为空时耦合。杂波本身的两维耦合特性决定了传统的一维频域滤波方法往往失效，一般必须在空时两维平面内进行滤波处理。空时自适应处理采用了空间和时间二维联合方式，自适应地滤除杂波和干扰，同时又兼具多通道雷达的灵活性，可以补偿系统误差的影响，因此可以有效改善系统的检测性能［4］。

工程中，杂波协方差矩阵往往不符合理想检测Brennan规则。论文将一些实际因素的影响引入算法中。

论文首先介绍了STAP 算法的基本原理，之后结合仿真实验，详细分析了实际工程因素对算法性能的影响。

1 STAP算法基本原理

STAP处理器是一个空间-时间两维域滤波器，同时处理空间和时间数据，在强噪声和杂波环境中检测目标信号。图1为空间时间二维数据。

图1 空间时间二维数据

空间数据来源于阵列的N 个阵元，时间数据来源于相干处理时间内的M 个脉冲。N 个阵元，M 个脉冲，以及L 个距离门的数据形成了N、M、L 三维数据立方体，包含了所有目标，杂波，干扰和噪声信息。把从每个距离门接收到的数据称为一张快照，连续的距离门数据就累积成为一个三维数据立方体，数据立方体用来查询各个距离门中是否存在目标。而自适应二维波束形成保证每个距离门的信噪比最大。图2 为三维数据立方体。

图2 三维数据立方体

1.1 空时导向矢量

任何时刻的所有天线单元输出都可以用空间导向矢量aN（θ）来表示。

式中：θ为接收方位角；T 为转置符号。与空间导向矢量类似，阵列中任何一个天线单元的所有M个脉冲输出都可以用时间导向矢量表示。时间导向矢量与多普勒频率相关。经计算得到时间导向矢量可表示为

式中：ωd为多普勒频率；与相对速度v有关。空时导向矢量为时间导向矢量bM（ωd）和空时间导向矢量aN（θ）的直积。

式中：⊗为克罗内克积。由式（3）可以看出，空时导向矢量与方位角θ、相对速度v有关。

1.2 杂波协方差矩阵

H1和H0分别表示目标信号存在和不存在两种假设，第j个距离门的数据可以表示为

式中：α为目标处的复散射系数；Xc表示干扰的总和，包括杂波及噪声。在同一个距离环r上，根据不同的方位角杂波环分为一系列杂波片。从不同距离片得到的所有杂波可表示为

式中：第1 部分代表K 个杂波片随机回波的总和，ck代表第k 个杂波片的随机幅度。第2部分n代表噪声矢量。

如果式（5）中随机幅度ck是均值为0，方差为σ2c的独立随机变量，则杂波为广义静止。杂波协方差矩阵可表示为

1.3 两维波束形成

为保证输出信号与杂波噪声功率比（SINR）最大，经计算可得权值w 的最优值，wopt为

式中：μ是一常数。输出功率为

实际工程中，杂波谱由大量杂波片集合而来，所以运动目标一般会淹没在杂波中不能被检测。图3 为基于STAP 算法的信号检测。如图3（a）所示，目标信号实际位于θt＝-25°，ωdt＝0.4，被大量杂波淹没，无法检测出来。图3（b）给出了应用STAP算法的检测结果，杂波抑制后目标凸显出来。

2 实际因素对STAP性能的影响

杂波特征谱是指对杂波协方差矩阵进行特征分解，并将特征值按大小秩序排列。图4为理想杂波特征谱。Brennan规则是指，在理想情况下杂波自由度（大特征值的个数）为N+M-1。杂波自由度越大，杂波越活跃，杂波抑制越困难。杂波自由度是进行杂波抑制所需系统自由度的参考依据。

图5为理想模型下SINR 曲线。曲线凹口越陡，说明最小检测速度（MDV，Minimum Detectable Velocity）越小，慢速运动目标检测效果越好。

图3 基于STAP算法的信号检测

图4 理想杂波特征谱

2.1 有源干扰的影响

在存在有源干扰情况下，干扰协方差矩阵由干扰、杂波和噪声三部分组成，表达式为

图5 理想模型下输出信杂噪比（SINR）曲线

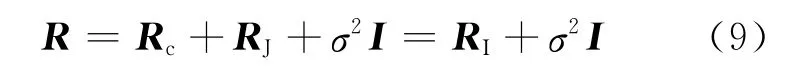
式 中：Rc表 示 杂 波；RJ表 示 有 源 干 扰；σ2I 表 示 白噪声；RI表示有色噪声，包括杂波和有源干扰；NJ表示不相关的有源干扰个数。协方差矩阵RJ的秩可表示为

图6为有源干扰对杂波特征谱的影响，从仿真结果可以看出干扰会使干扰自由度增大，使协方差矩阵的秩增大。假设存在两个不相关干扰，M＝16，则协方差矩阵RJ的秩Rank（RJ）＝2×16＝32。

图6 有源干扰对杂波特征谱的影响

2.2 通道失配的影响

通道失配对杂波协方差矩阵的影响可表示为

式中：T 为失配因子，是半正定Hermitian矩阵。通道失配会改变干扰协方差矩阵的特征值和特征矢量。建立式（12）和式（13）模型来描述通道失配，其中p（δεi）和p（φi）分别表示幅度和相位误差的概率密度函数。通过计算得到失配因子，如式（14）所示，进而得到杂波协方差矩阵。图7为通道失配对特征谱和SINR的影响。

图7 通道失配对特征谱和SINR 的影响

比较三种通道误差存在时的干扰／杂波特征谱和输出SINR 的仿真结果。

由仿真结果可以看出，通道不匹配时，杂波自由度增大，SINR 损失并且不稳定。随着阵元误差量级变大，杂波自由度明显增加。这说明天线通道误差使杂波去相关，引起大量伪杂波，而且误差越大，伪杂波越多。输出SINR 特性也随着阵元误差量级和伪杂的增加而恶化，MDV 变大。

2.3 天线色散的影响

带宽引起的天线色散是通道失配的主要成因之一。协方差加权矩阵T 与θ 有关。

在均匀线阵中，第k 个阵元和第n 个阵元之间的时延可表示为

假设有限带宽为B（Hz），相应的自相关函数r（τ）的表达式为

协方差加权矩阵可表示为

式中：θ 表示主波束指向。图8 为天线色散对干扰特征谱和SINR 的影响。其中，信杂比为30dB，fc＝1GHz，B＝100 MHz。图8显示色散对于杂波自由度的影响非常大。杂波自由度变大，伪杂波增加，MDV 变大。

2.4 杂波起伏的影响

杂波起伏会导致杂波自由度增大。杂波起伏是由 杂 波 内 部 运 动（Internal Clutter Motion，ICM）引起的，在实际中，地面植被或海浪随风运动会引起杂波起伏。Billingsley模型能够很好地描述杂波起伏的特性。

图9为ICM 对特征谱和SINR 的影响，风速为15 mph，信杂比为60 dB，采样频率fr＝1kHz，与风速有关的形状参数b＝5.7。

图9显示信杂比较大时，杂波起伏对特征谱的影响较明显，杂波起伏导致杂波自由度增加，杂波自由度越大，输出SINR 凹口展宽，MDV 越大，整体检测性能越差。

图8 天线色散对特征谱和SINR 的影响

图9 ICM 对特征谱和SINR 的影响

3 结束语

本文介绍了STAP 算法的基本思想，详细分析了有源干扰、通道失配、杂波起伏等实际因素对算法性能的影响。仿真结果说明，当这些工程中常见影响因素存在时，杂波自由度增大，杂波去相关。或者可以认为这些因素引起了大量伪杂波，而且误差越大，伪杂波越多，输出SINR 损耗变大，STAP 算法的整体检测性能随之恶化。

［1］ Melvin，W.L.A STAP Overview［J］.Aerospace and Electronic Systems Magazine，2004，19（1）：19-35.

［2］ Entzminger JN，Jr.，Fowler CA，Kenneally WJ.JointSTARS and GMTI：Past，Present and Future［J］.Aerospace and Electronic Systems，IEEE Transactions on，1999，35（2）：748-761.

［3］ 王永良，彭应宁.空时自适应信号处理［M］.北京：清华大学出版社，2000.

［4］ Guerci JR.Space Time Adaptive Processing for Radar［M］.Boston：Artech House，2003.

［5］ Klemm R.Principles of Space-time Adaptive Processing［M］.London：The Institution of Electrical Engineers，2002.