小题大作话“折叠”

☉江苏省东台市教育局教研室 周玉俊

小题大作话“折叠”

☉江苏省东台市教育局教研室 周玉俊

一、课本题解析

原题在线：新苏科版（七）下第42页复习题第19题.

如图1，把△ABC纸片沿DE折叠，使点A落在四边形BCDE内部点A′的位置，∠A′与∠1+∠2之间存在怎样的数量关系？为什么？

本题在设计思路和解题策略上具有一定的导向性，所以分析好本题的解题思路往往能起到举一反三、触类旁通的作用.下面让我们一起对∠A′与∠1+∠2之间的关系进行探究.

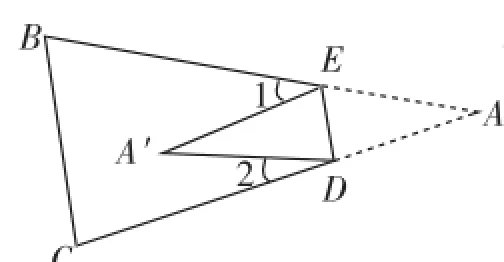
图1

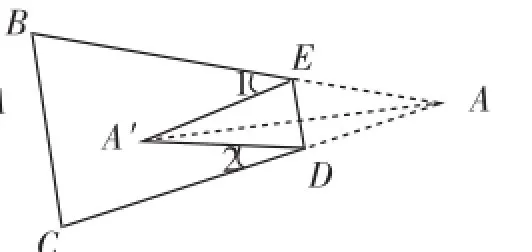
图2

思路1：如图1，由四边形AEA′D可知∠A+∠AEA′+∠A′+∠A′DA=360°.

由平角的定义可知：∠1+∠AEA′+∠2+∠A′DA= 360°.

所以∠1+∠2=∠A+∠A′.

由折叠得：∠A=∠A′，即∠1+∠2=2∠A′.

思路2：如图2，连接AA′，由三角形外角的性质可知：

∠1=∠EAA′+∠EA′A，∠2=∠DAA′+∠DA′A.

所以∠1+∠2=∠EAA′+∠EA′A+∠DAA′+∠DA′A=∠A+∠A′.

即∠1+∠2=2∠A′.

点评：思路1中巧妙地运用了两个平角的和及四边形的内角和均为360°来探寻∠A′与∠1+∠2之间的关系；思路2中主要通过构造三角形，运用其外角的性质进行转化.两种方法思路虽然不同，但都达到了沟通∠A′与∠1+∠2之间关系的目的.

二、演变与探究

除了对∠A′与∠1+∠2之间关系进行探究，能否对折叠的方式进行适当的变化，让探究继续进行下去呢？下面，我们一起来看看这样几种变化.

探究一：改变折叠后点的落点位置，使点落在四边形外部

如图3，若把△ABC纸片沿DE折叠，使点A落在四边形BCDE外部点A′的位置，则∠A′与∠1、∠2之间又有怎样的数量关系呢？

图4

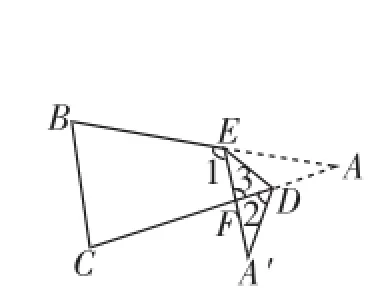
图3

思路分析：运用原题中的思路2，寻找三角形的外角进行转化.

由∠1是△AEF的外角，得∠1=∠A+∠3.

同理，∠3=∠2+∠A′，则∠1=∠A+∠2+∠A′.

由于∠A=∠A′，则∠1-∠2=2∠A′.

如图4，若把△ABC纸片沿DE折叠，使△A′DE覆盖点C，且点A落在四边形BCDE外部，则∠A′与∠1、∠2之间的数量关系是否发生变化？

思路分析：延长AC交EA′于F点，与图3相比，A与C点的相对位置发生了变化，但∠1与∠EFA、∠A的关系，∠EFA与∠2、∠A′的关系始终保持不变，故∠A′与∠1、∠2之间的数量关系没有发生变化，仍然为：∠1-∠2= 2∠A′.

点评：与原题相比，图形的位置发生了改变，∠A′与∠1、∠2之间的数量关系也发生了变化，但用外角来转化的方法并未改变.

探究二：折叠三角形的三个角，使折叠后的三个顶点落在三角形内部同一点处

如图5，同样地，把一个三角形纸片ABC折叠3次，使3个顶点重合于纸片的同一点P.试探究此时∠1+∠2+∠3+∠4+∠5+∠6=______°.

思路分析：由折叠得：∠A=∠EPD、∠B=∠FPG、∠C=∠HPI.由∠A+∠B+C=180°，得∠EPD+∠FPG+∠HPI=180°.

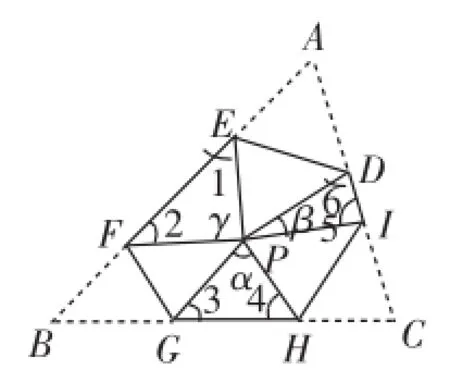
图5

则∠α+∠β+∠γ=360°-180°=180°.

由于△EFP、△GHP、△IDP的内角和均为180°.故∠1+∠2+∠3+∠4+∠5+∠6=3×180°-（∠α+∠β+∠γ）= 360°.

点评：由课本习题中的折叠三角形的一个角，演变为折叠三个角，其变化自然，题目源于课本，却又高于课本，解题时只需抓住折叠前后的不变量及三角形的内角和定理即能解决问题.

探究三：折叠三角形的三个角，使折叠后的三个顶点落在三角形内部，但不在同一点处

图6

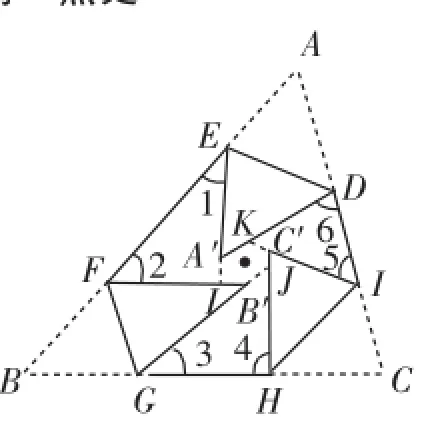
图7

如图6，如果把三角形纸片ABC折叠3次，3个顶点不重合于同一点P，那么在探究二中关于“∠1+∠2+∠3+∠4+∠5+∠6=360°”的结论是否仍然成立呢？

思路1：如图7，延长EA′、GB′、IC′，分别交FB′、HC′、DA′于点I、J、K.六边形A′IB′JC′K的六个外角之和为360°.由折叠得：∠EA′D+∠FB′G+∠HC′I=∠A+∠B+∠C= 180°.

所以∠EIF+∠GJH+∠IKD=180°.

由△EFI、△GHJ、△IDK三个内角的和为540°，得∠1+∠2+∠3+∠4+∠5+∠6=540°-180°=360°.

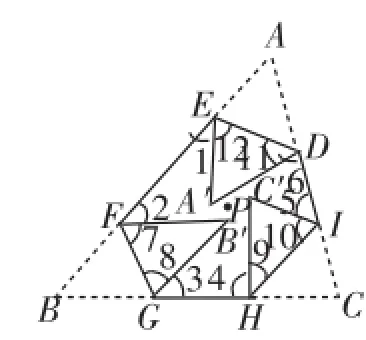
图8

图9

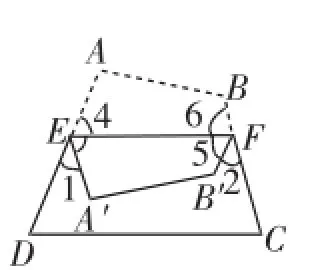
图10

思路2：如图8，在△FGB′、△HIC′、△DEA′中：

∠7+∠8+∠B′+∠9+∠10+∠C′+∠11+∠12+∠A′= 3×180°=540°.

∠7+∠8+∠9+∠10+∠11+∠12=540°-（∠A′+∠B′+∠C′）=540°-180°=360°.

由六边形DEFGHI的内角和为720°，得∠1+∠2+∠3+∠4+∠5+∠6=720°-（∠7+∠8+∠9+∠10+∠11+∠12）.

即：∠1+∠2+∠3+∠4+∠5+∠6=720°-360°=360°.

点评：由折叠后的三个顶点落在三角形内部同一点处到不落在同一点处，体现了从特殊到一般的数学思想方法，在解题思路上离不开六边形的内角和、折叠前的角等于折叠后的角等基本的解题方法.

探究四：由折叠三角形类比折叠四边形

若将三角形纸片改成四边形纸片，如图9，将四边形ABCD纸片沿EF折叠，使点A、B落在四边形EFCD的内部时，∠1+∠2与∠A、∠B之间又有何数量关系呢？

思路分析：如图10，在四边形ABFE和四边形A′B′FE中：

∠A+∠B+∠6+∠4=360°，∠A′+∠B′+∠5+∠3= 360°.

所以2∠A+2∠B=720°-（∠3+∠4+∠5+∠6）①.

由∠1+∠3+∠4=180°，∠2+∠5+∠6=180°，所以∠3+∠4+∠5+∠6=2×180°-（∠1+∠2）②.

把②代入①得：2∠A+2∠B=720°-360°+∠1+∠2.

则∠1+∠2=2∠A+2∠B-360°.

点评：以“折叠产生的不变量”为基础，运用探究一中的解题思路，抓住两个平角及四边形的内角和为360°即可解决问题.

三、思考及感悟

习题教学要注重引导学生进行充分的变式探究.数学家波利亚说过：一个有责任心的教师与其穷于应付烦琐的数学内容和过量的题目，还不如适当地选择某些有意义又不太复杂的题目去帮助学生挖掘题目的各个方面，在指导学生解题的过程中，提高他们的才智和推理能力.通过以上探究，我们的感悟是：在平时教学过程中，我们不能仅仅满足于对课本题的简单掌握，习题教学要学会“小题大作”，把一个简单的数学问题，通过变式使问题逐步加深，变成问题串，让学生在解决问题的过程中学到数学方法、深化数学思维，只有真正让学生领悟解题的思路，掌握解题的方法，才能不断提高分析问题和解决问题的能力，提升他们的数学核心素养，真正达到学以致用的目的.

解题过程中要让学生亲历“数学化”思考的过程.数学课堂必须使学生有机会真正经历“数学化”，这已成为越来越多的教师的共识.因此，教学中应采用多种教与学的方式，让学生在独立思考、探究学习、合作交流中学会学数学，用数学的思想、方法，创造性地解决问题，并在亲历“数学化”过程中获得多种体验.折叠是一种对称变换，其本质上属于轴对称.折叠前后图形的位置发生变化而形状和大小不变.对于折叠较为复杂的问题，可以让学生先实际操作，在此基础上画出折叠前后的图形，这样便于找到图形折叠前后的数量和位置关系，继而从中抽象出基本图形和基本规律，找到解决这类问题的共性的方法.

总之，在数学课堂教学中，遵循学生认知的发展规律，根据教学内容和目标加强变式训练，对巩固基础、培养思维、提高能力有着重要的作用.教学中要特别重视对课本例题和习题的“改装”或引申.当然，课堂教学中的变式题最好以教材为源，以学生为本，体现出“源于课本，高于课本”的特点，并能在日常教学中更多地渗透到学生学习中去.同时，引导学生也尝试“变题”，使他们自己去探索、分析、综合，以全面提高学生的数学素质.Z