寻几何阅读之道,建高效课堂
——从一道几何习题说起
寻几何阅读之道,建高效课堂
——从一道几何习题说起
☉浙江省宁波市兴宁中学徐积国
笔者在教学七年级“几何的初步认识”这一章时,作业上出现了这样一道题:
“如图1,已知O在直线AB上,OE⊥OC,OD是∠COE内一条射线,则图中互余的角共有_______对.”
笔者所教授两个班答题情况统计如下表所示

答案班级6 4 2其他A班(4 8人)1 8人1 6人1 0人4人B班(4 9人)1 6人1 7人9人7人
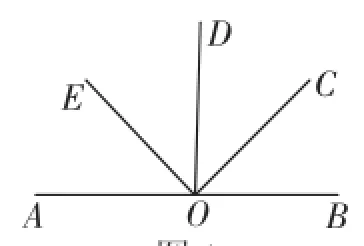
图1
这道题出错普遍,笔者课后做了调查,答案为6的学生的主要错误在于他们认为∠AOE、∠DOE、∠COD、∠BOC都是45°;答案为4的学生的主要错误在于他们认为这样的图再熟悉不过了,认为OE、OC分别是∠AOD、∠DOB的平分线.这引起了笔者的反思.如果学生能认真阅读题目、审清题意,解决这样的问题应该不难.一方面学生本身对阅读缺乏必要的阅读习惯与耐心,另一方面学生缺乏必要的阅读方法与技巧.因此,教师在课堂教学中,应该有意识地渗透重视数学阅读的理念,引导学生学习数学阅读方法与技巧去解决问题,从而提高课堂效率.以下是笔者在几何教学中指导学生数学阅读的策略.
一、阅读之道,有加有减
数学阅读可以借鉴语文课的一些阅读技巧,如“提主干”“缩句”“长句改短句”等,这样可以帮助学生理解,抓住要领.
1.添加文本,结构清晰
数学课本上经常出现一些精简的概念或定理,学生有时觉得理解困难.如果适当地添加某些用词,长句分成短句,形成一个完整的句式,学生往往比较容易理解,阅读思路就变得顺畅.
例1命题“到线段两端点距离相等的点在这条线段的垂直平分线上”转换成“如果有一个点到一条线段两端点的距离相等,那么这个点在这条线段的垂直平分线上”.如果长句分成短句,条件、结论清晰,易于理解.再由已知画出图形(如图2),之后将文字语言中的条件与结论用符号语言表示,就更加清晰了.

图2
2.删减枝叶,理清要点
一些几何问题中包含有问题的背景知识,或为了严谨性文字描述较多,在读题时可以根据情况删除这些内容,以便快速抓住有效信息.
例2勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了两枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在图3所示的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R= 90°,点H在边QR上,点D、E在边PR上,点G、F在边PQ上,那么△PQR的周长等于______.
阅读策略:删除背景知识①,在对照图形得到“共线”的情况下删除②.
①勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了两枚以勾股图为背景的邮票.所谓勾股图,是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在图3所示的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,②点H在边QR上,点D、E在边PR上,点G、F在边PQ上,那么△PQR的周长等于______.
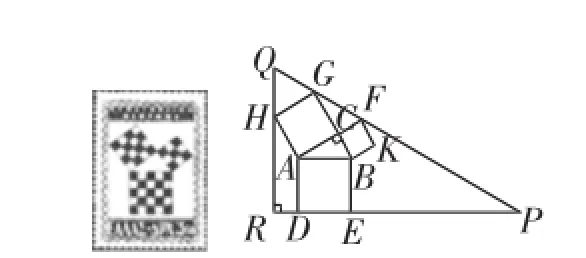
图3
二、解剖图形,清晰明了
图形文本与文字文本、符号文本等丰富了数学文本内容.直观、便于观察、富有想象是图形文本的特点,是视觉语言,所以破译图形文本也是很有必要的“.破译”图形文本,可根据要求从以下几个方面着手.
1.“标示”符号,观察便捷
2.分解图形,化繁为简
数学新课标指出:“能从复杂的图形中抽离简单的基本图形”,往往要先从分析简单图形的性质出发,再综合几个简单图形相应的结论.
例3如图4,BE平分∠ABD,CF平分∠ACD,BE与CF交于G,若∠BDC=140°,∠BGC=110°,则∠A= ________.
不少学生初看此图形,发现各种线错综复杂,求∠A不知从哪里入手.为了辅助学生拨开错综的线条,笔者指导学生按如下方式去阅读.
(1)∠BDC=140°、∠BGC=110°为已知角,请同学们局部观察∠BDC与∠BGC可以放在怎样的图形之中.学生容易想到凹四边形BDCG(如图5),得到结论∠BDC=∠1+∠2+∠BGC,从而得到∠1+∠2=30°.
(2)∠1+∠2=30°和什么条件有联系?学生容易想到角平分线这一条件,从而得到∠ABG+∠ACG=30°与∠ABD+∠ACD=60°.
(3)请同学们思考∠A放在怎样的图形之中.学生自然地想到凹四边形BDCA(如图6)与凹四边形BGCA.以图6为例,∠ABD+∠ACD+∠A=∠BDC,立刻得到∠A= 80°.
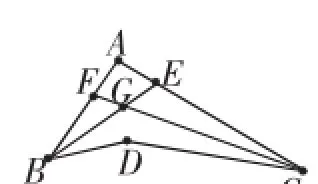
图4
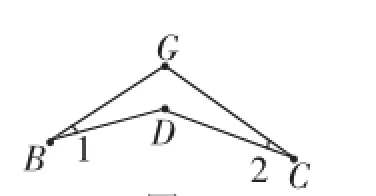
图5
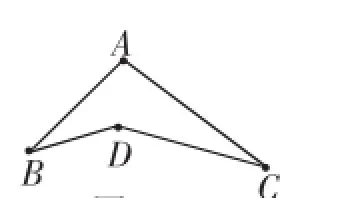
图6
3.“着色”强调,排除干扰
几何图形常见处理方式就是分割、补形、折叠,通过对图形的这些直观处理,一般能辅助解题,使解题过程简捷、明快.在对图形的分割、补形、折叠中提高阅读几何图形的能力.对一些复杂的图形,可以用不同阴影部分突出要研究的部分图形,排除其他图形对视觉的干扰作用.
例4在学习勾股定理之后,出现了这样一道题.如图7,分别以Rt△ABC的三条边为直径作半圆,结论:“两个月牙形的面积之和,等于△ABC的面积,即S1+S2=S3.”你能说明理由吗?

图7

图8
阅读策略:(1)S1、S2这样的图形有相应的面积公式吗?(2)涉及图形面积,我们有时要对图形进行分割或补形,从而形成可利用面积公式表达的图形.对于S1+S2,割形还是补形?补形对学生而言很好理解.(3)如图8,设阴影部分的面积为S,再由勾股定理推出“S1+S2+S=S3+S”也就顺理成章了.
三、翻译数学语言,多视角进行阅读
“数学教学也是数学语言的教学”.几何阅读时若能将三种语言“文字语言、符号语言、图形语言”灵活地互相转化,则意味着看问题多了一个视角,更方便去解决问题.要培养学生一定的几何阅读能力,需引导学生在“文字语言、符号语言、图形语言的转化上”有一定的策略.
1.文字、图形语言反复转化——双向转化,加深理解
文字语言能精确地表达含义,但有时较抽象,而图形语言形象、直观.若两种语言之间互相转化,则既有感性认识又不失理性认识,既可做到形象、直观,又能精确、严谨.
例5判断题:若PA=PB,则点P是线段AB的中点.
这是一道典型题,学生很容易出错.产生这种错误的原因是学生没有真正理解题目的意思,用自己经验中的图形代替了题意中的图形,从而产生了错误.从数学阅读的角度入手,对学生进行有效指导十分必要.
阅读策略:
(1)请同学们按照题意画出图形.很多同学画出了这样的图(如图9)
(2)请同学们精确描述图9.
生:PA=PB.
师:数量关系描述的很准确,几何中还有怎样的关系?
生:位置关系.
师:有补充吗?
生:点P在线段AB上,PA=PB.
师:那你们说这句话“若PA=PB,则P是AB的中点”对不对呢?能画出怎样的图?
生:不对.
很多学生最后能画出如图9与图10所示的两种图.
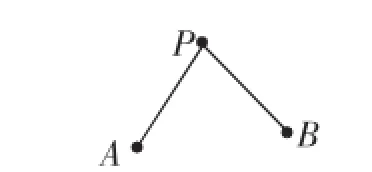
图10
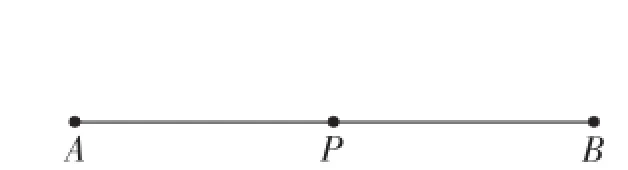
图9
2.文字、符号、图形交互——聚焦条件,形象、直观
一些几何问题条件较多,比较凌乱,将一部分条件有效地翻译成符号语言,尽可能将文字条件与已翻译的符号语言直观地显示在图形中,这样有利于降低难度.
例6如图11,已知O在直线AD上,OE⊥OB,OC是∠BOE内一条射线,OD平分∠FOE,若∠DOE=2∠BOC,∠BOC比∠COE小20°,求:
(1)∠COD的度数;
(2)∠AOF的度数.
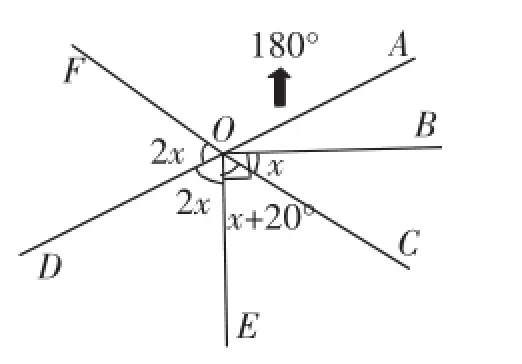
图12
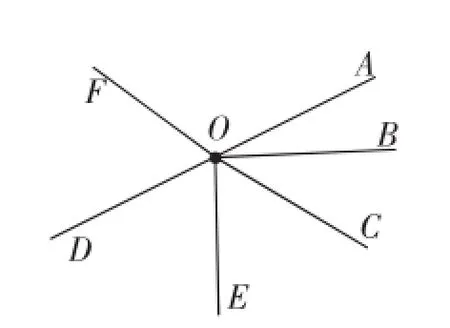
图11
阅读策略:将文字语言描述的条件转化成符号语言与图形语言,使条件较多、有难度的几何问题便于观察.
(1)理清条件(文字语言):如图12,已知O在直线AD上,OE⊥OB,OC是∠BOE内一条射线,OD平分∠FOE,若∠DOE=2∠BOC,∠BOC比∠COE小20°.
(2)将划线部分转化成符号语言与图形语言.
本题中涉及的数量关系较多,用列方程解决问题.不妨设∠BOC=x.
O在直线AD上⇒图12中涂黑直线AD,有180°;
∠BOC比∠COE小20°⇒∠COE=x+20°;
∠DOE=2∠BOC⇒∠DOE=2x;
OD平分∠FOE⇒∠DOF=2x;
OE⊥OB⇒图12中作直角标记.
(3)符号语言与图形语言交互:将表示∠COE、∠DOE、∠DOF的代数式标记在图12中.
(4)由图12中的信息很容易列方程:x+x+20°=90°.
四、整体阅读,事半功倍
“注意分散效应”给我们启示:“多种视觉信息源之间会导致注意力分散,用一个整合的信息源来代替多种信息源”.有些几何图形经常出现,对解决其他问题作用明显,我们称这类图形为基本图形.引导学生将看似分散的、无序的、凌乱的条件作为整体来阅读,用基本图形解决问题事半功倍.
例7如图13,△ABC中,∠ABC的角平分线与△ABC的外角平分线交于点D,作DF∥BC分别交AC、AB于点E、F,找出图中所有的等腰三角形.

图13

图14
在对题目的分析过程中,由条件联想到有关基本图形,构造出相应的基本图形,利用其结论解决问题.(1)在八年级上册等腰三角形教学中,角平分线+平行线一定有等腰三角形就是常见的基本图形,如图14,已知BO为∠ABC的角平分线,且OD∥BC,则△BOD为等腰三角形.(2)由已知条件容易想到模型,得到等腰△DBF与△CDE.
五、破解动态几何问题——动中取静,先分再合
动态几何问题是平面几何中较复杂的一类问题,其运动方式主要有点、线、面的平移、翻折、旋转三大类,经常把数与几何、函数与几何、函数与面积等综合起来.运动变化引起了图形的形状、大小、位置等的变化,在静态状态下,很难分析图形的变化情况.笔者引导学生阅读动态几何的策略如下所示.
(1)用多媒体工具直观演示.
(2)动中取静.
所谓动中取静,指的是在运动的过程中,某一时刻图形是静止的,而这一时刻图形的性质特征与局部一段时间内的关系是不变的.如何取静?抓住特殊图形特征或图形形状的改变等适当画图,使其直观呈现出来,画图时还需注意做到有序性,以免遗漏一些情况.
(3)将每个静的情况逐一击破,最后再综合起来
例8如图15(1),点A、B在直线MN上,AB=11厘米,⊙A、⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)试写出点A、B之间的距离d(厘米)与时间t(秒)之间的函数表达式;
(2)问:点A出发后多少秒两圆相切?
阅读指导:第一步:借助几何画板直观呈现出其运动状态;
第二步:按照上述取静的规则画出草图:图15(2)-图15(9).
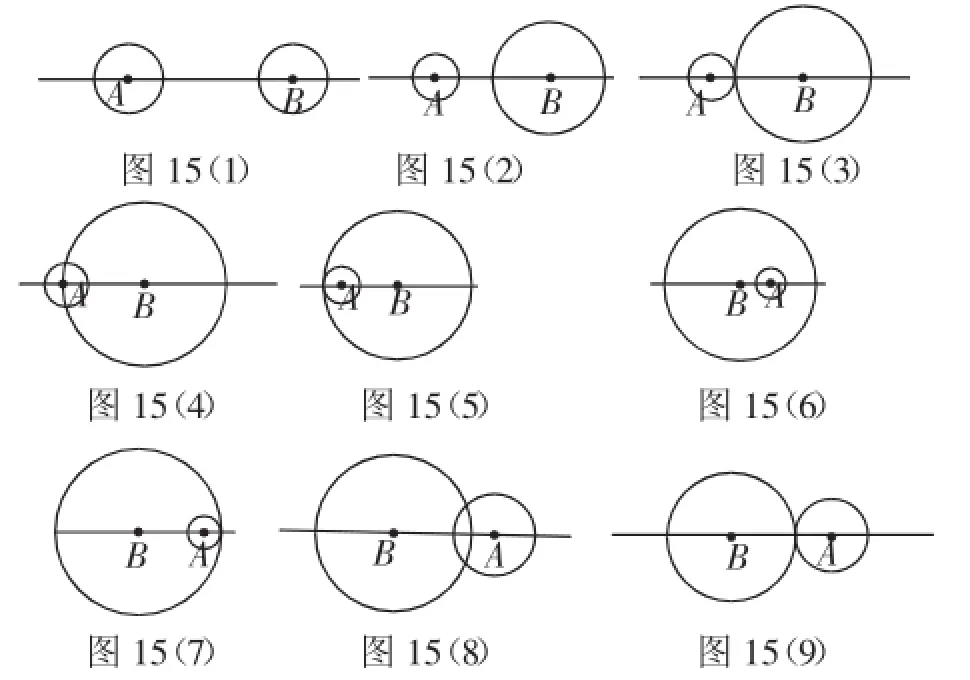
第三步:由画的图得出解答过程.
为了帮助学生更好地阅读动态几何问题,笔者就经常利用几何画板动态演示,渗透阅读策略,让学生观察,发展到最后学生自己动手画.
六、反思
笔者一直在思索如何构建高效课堂,让学生远离“题海战术”,较轻松地、有效率地学习,同时让学生既获得数学知识,又收获一些数学方法.如何达成这样的目标?没有永恒的方法.关键在于老师对细节的完美追求,能够持续地反思改进,善于处理学生学习不理想的细节、老师教学的细节.本文正是基于学生在几何阅读方面能力欠缺这一细节启发下完成的.
几何阅读能力的形成是一项长期的循序渐进的过程,它需要我们平时注意培养数学阅读习惯,需要教师在教学中大胆探索、积极尝试,勤于思考,加强阅读方法指导.几何阅读能力培养应以几何问题为载体,渗透在平时的课堂教学中.通过几何阅读能力培养促使学生形成主动学习、自主探究的习惯,从而提升课堂效率.
1.徐小建.把握4种语言,准确理解题意[J].中国数学教育,2011(7).
2.中华人民共和国教育部.全日制义务教育数学课程标准(实验稿》[M].北京:北京师范大学出版社,2001.
3.范良火,主编.义务教育课程标准实验教科书·数学[M].杭州:浙江教育出版社,2005.
4.赵山龙.做一个“善于举例”的数学教师——来自一线教师的认识、实践与思考[J].中学数学(下),2012(5).Z

