在潜移默化中养成学生发现和提出问题的意识

在潜移默化中养成学生发现和提出问题的意识

☉福建省泉州市鲤城区教师进修学校 曾泽群

创新是一个民族进步的灵魂，是国家兴旺发达的不竭动力.创新型人才必须具有发现和提出问题的能力.基于此，《义务教育数学课程标准》（2011年版）将“提高发现和提出问题的能力”写入课程目标里，与“提高分析和解决问题的能力”并驾齐驱，处于同等地位.因此，我们的教学就不能只停留在分析与解决问题的层面上，而应该着力创设能引领学生发现和提出问题的背景，使他们在观察与思考的基础上，在尝试中实现飞跃.下面笔者从引出探索新知问题的背景切入，谈谈如何创设情景，如何在潜移默化中培养学生的问题意识.具体的思考与做法如下.

一、创设隐含数学问题的生活背景，引领学生发散式提出问题

数学源于生活，又服务于生活.生活中处处有数学，已是不争的事实.为了让学生学会从数学的角度去观察生活中的对象、去思考对象的本质特征，发现并提出、分析和解决与数学有关的问题，在教学中，教师可以根据教学内容，挖掘与之相符且学生熟悉的生活素材，创设隐含数学问题的生活背景，以便学生发现和提出与数学有关的问题.

案例1：矩形的概念.

生活中不乏矩形的实例，鉴于矩形是平行四边形的特例，在“矩形的概念”教学问题的提出中，笔者选择了校园的伸缩门，以它为背景，引领学生发现和提出问题.具体如下：

反思性材料：学习平行四边形以后，当你们背着书包进出校门时，对于校门口的伸缩门（如图1）是熟视无睹？还是浮想联翩？今天，我们的学习就从校门口的伸缩门及它的基本图形（图2）开始.想一想，从它们的伸缩过程中，你能提出哪些与数学有关的问题呢？

图1

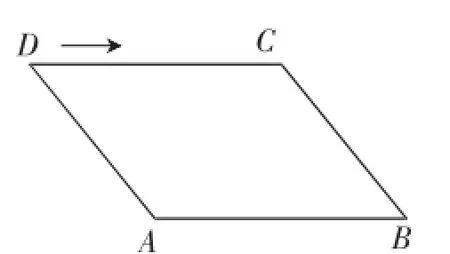
图2

伸缩门，学生既熟悉又陌生的生活背景，熟悉是因为现实生活中随处可见，陌生是由于学生从未将它与数学联系在一起，从伸缩门及其基本图形的伸缩过程中，思考与数学有关的问题.当学生面对这一反思性材料时，他们需要用运动变化的观点去观察事物，并进行发散式思考，进而才有可能提出实质性的数学问题.互动中，既要让学生发表他们的所思所想，也要有教师用思维引领学生参与问题讨论，以便提出与本课教学内容——矩形的概念接轨的问题.

问题1：构成伸缩门的基本图形（图2）的形状是什么？伸缩门之所以能伸缩，它应用了哪种图形的什么性质（或伸缩门的原理）？

问题2：拉动伸缩门的过程中（即推动图2中的点D），它的基本图形（图2）中哪些数学元素发生了变化，哪些不发生变化？

问题3：（教师进而提出条件、结论开放的问题）拉动伸缩门的过程中（即推动图2中的点D），基本图形（图2）也在变化，在这一变化的过程中，是否有我们曾经熟悉的、更为特殊的图形出现？若有，画出它的草图并写出它出现的条件.让学生作进一步的思考，以便经历矩形概念的形成过程.

由于引领“学生发现和提出问题”的背景来自生活，学生对它的感悟与认识因人而异，可谓仁者见仁，智者见智，以致学生所提的问题内容具有发散性，因此，互动中，教师的思维引领与问题参与是非常必要的.唯有如此，学生的思维才能由发散到聚焦，才能对如何提出有研究价值的问题有所感悟.这种学生的尝试与教师的引领示范有机结合的问题提出模式，对养成学生发现和提出问题的意识起着关键的作用.

二、创设隐含数学问题的操作实验，引领学生根据实验现象提出问题

试验可以获得结论，透过现象看本质，往往又能提出有价值的问题.由于许多几何结论都是通过“操作确认并辅以数学说理”来获得的，因此，在几何教学中，教师可针对具体内容，结合学情与教学目标，设计一些操作活动，由学生亲自动手做实验，然后根据实验出现的现象，从中获得一些较为浅显的结论，进而尝试着提出实质性问题.

案例2：三角形三边关系.

根据三角形的定义，对于任意的三条线段，只要动手操作，摆一摆，就能判定它们能否构成三角形，进而就能引出探究三角形三边关系的问题.对此，在“三角形三边关系”教学问题的提出中，笔者设计了一个动手实践与反思的活动，引领学生提出问题.具体如下：

（1）操作活动：请同学们从预先准备的八根小棒（其中三根小棒长度均为4 cm，另五根小棒长度分别为2 cm，3 cm，5 cm，6 cm，7 cm）中任意取出三根摆三角形（至少五次以上），并记录每次所取三根小棒的长度及实验操作的结果.

（2）活动反思：根据实验操作所获取的数据及对应的结果，想一想你能从中得出什么结论并提出相关的探索问题.

让学生动手操作摆三角形，虽是一个浅显的活动，而后的活动反思则具有思维含金量，它不但能活跃学生的思维，而且能激起学生的问题意识.学生通过对操作结果——两种对立现象（①不能构成三角形，如：2 cm，3 cm，5 cm与2 cm，3 cm，6 cm.②能构成三角形，如：4 cm，4 cm，4 cm（等边三角形）；4 cm，4 cm，7 cm（等腰三角形）；4 cm，3 cm，5 cm（直角三角形）；7 cm，6 cm，5 cm（锐角三角形）；7 cm，6 cm，3 cm（钝角三角形））的思考，得出结论：“并不是任意的三条线段都能组成一个三角形.”进而提出新的探索问题：“怎样判断三条线段是否能构成一个三角形？”或另一个等价的问题：“已知两条线段，第三条线段怎样选择，才能构成一个三角形？”体验了根据实验现象，获取结论或提出问题的全过程.并确立其问题解决的途径：“收集实验结果所对应的数据，并加以分析、概括、说理.”

由于引领“学生发现和提出问题”的背景来自学生实验的结果，而实验结果的单一性（非此即彼），为学生自主提出与教学内容接轨的问题创造了有利的条件.鉴于此，由学生唱主角提出问题，教师在互动中帮助学生完善问题是最佳的选择，有助于提升学生发现和提出问题的能力.这种以学生为主体的问题产生方式，对养成学生发现和提出问题的意识起着重要的作用.

三、创设隐含数学问题的直观图形，引领学生凭借直觉思维提出问题

由于图形的直观可视性能给学生提供猜想与探索的直觉思维，而数形结合又是重要的解决问题的方式，鉴于形的性质往往可以利用数式来体现，数式的问题也可借助形来解决，在教学中，教师可选择一些有“形”的教学内容，通过创设隐含数学问题的直观图形，为学生发现与提出问题创造有利的条件.具体如下：

案例3：一次函数的性质.

直角坐标系为形数互化创造了有利的条件.由于一次函数的性质包含图像性质与变量间的关系两部分.为此，在“一次函数的性质”教学问题的提出中，笔者以画一次函数的图像为背景，设计了一个引例，学生对图像作进一步观察后，能大胆地提出问题.具体如下：

（1）引例：按符号的不同对一次函数表达式y=kx+b（k≠0）中的k、b分类，再分别写出其各种类型的具体的一个一次函数，并在同一坐标系中画出它们的图像.（此内容可以安排在课前完成）

（2）反思：观察你所画的每个一次函数图像的变化趋势，你发现了什么数学现象，能从中提出什么探索问题？从形化数的角度，你还能提出什么问题？

学生动手画图，不是纯粹的简单的技能操作，它渗透了分类思想.学生必须以分类思想为指导，才能从中准确地选出每一类的代表，为后续的探究起到以点带面的效果.从画图到对图形的反思，它将发现和提出问题的机会留给学生，促使学生的思维上了一个台阶.

图3

由于引领“学生发现和提出问题”的背景来自直观可视性图形，凭直觉与本能，学生可以提出问题，但对问题表述可能不像问题①那样到位，而“形化数”的提示虽为学生再提出问题②提供了思维的方向，但还是离不开教师的有效引导.这种根据学生的实际反应情况，适当给予帮助的助学方式，有利于提高学生发现与提出问题的能力，对养成学生发现和提出问题的意识起着促进的作用.

四、创设隐含特殊性数学问题的题组，引领学生在比较中提出问题

事物中存在着特殊与一般的关系，从一般中发现特殊，进而寻求其规律，使运算或求解过程简便.这种现象在数学中普遍存在.为了让学生能在普遍性中发现其特殊性，进而获得新知，在教学中通过选择一些特定的例子，由学生在求解后的比较中发现特殊性，进而提出研究的问题.

案例4：平方差公式.

由于平方差公式是多项式乘以多项式法则的特例，因此在“平方差公式”教学问题的提出中，笔者刻意选择了一组能承上启下的整式乘法计算题，让学生在比较运算结果的项数中发现和提出问题.具体如下：

（1）计算：①（a+b）（c+d）；②（x+1）（y+2）；③（x+1）·（x+2）；④（2a-3b）（2a+3b）；⑤（3x+4）（3x-4）；⑥（x+2）·（x-2）.

（2）反思：观察、比较计算结果的项数，你发现了什么？你能从中提出进一步探索的问题吗？

利用“两数和乘以两数差”与“多项式乘以多项式”是特殊与一般的关系，设计了让学生发现和提出问题的背景——一组计算题及其反思.从计算到反思，促使学生从技能操作转到思维的层面，学生通过对计算结果的比较，发现计算结果的项数有所不同，并有规律性，从而提出探索问题：“具有什么形式的多项式乘以多项式，其运算结果只有两项.”进而转入对题目结构的分析，解决问题，获得新知.

由于引领“学生发现和提出问题”的背景是学生熟悉的题目，但是学生对它们之中是否存在简便计算规律的研究意识薄弱，而这种意识恰恰又是创新的表现.因此，采取计算的方式，通过感悟结果的简洁度，提出探究问题，切合学生的当前思维，有效提高了他们发现与提出问题的能力，对养成学生发现和提出问题的意识起着有益的作用.

五、创设隐含数学问题的导语，引领学生在类比中提出问题

类比是数学中常见的推理方式之一，对于其探究方式或基本知识有相似之处的两类内容，我们通常采用类比的方法，从已知的一类（已解决的问题、已获得的知识、已积累的数学活动经验等）出发，提出另一类的探索问题，由此可见，类比也是学生提出探究问题的引路人.

案例5：相似三角形的判定.

相似是全等的推广，两者的学习方式相类似，在“相似三角形的判定”教学问题的提出中，笔者将它与全等三角形的判定进行类比，引导学生猜想提出三角形相似的判定条件，进而论证猜想.具体如下：

导语：上一节我们学习了相似三角形的有关概念，了解了相似三角形与全等三角形的关系是一般与特殊的关系，学会了利用相似三角形的概念来判定两个三角形相似，请同学们回忆三角形全等的判定条件的探索过程，想一想对于两个三角形相似，我们下一步的研究目标是什么？

短短的导语看似简单，但它隐含着类比推理，学生凭借探究三角形全等的判定条件所积累的活动经验，以类比为指导思想，就可以提出进一步研究的问题：判定两个三角形相似是否需要这么强的条件（三角对应相等、三边对应成比例）？怎样削减？随即类比全等三角形的判定方法提出以下猜想：

（1）两角对应相等的两个三角形相似；

（2）两边对应成比例且夹角相等的两个三角形相似；

（3）三边对应成比例的两个三角形相似.

由于引领“学生发现和提出问题”的导语已为学生类比提出探究问题指明了方向，学生完全有能力自主地提出问题，教师的鼓励可增强其信心.这种脱缰式的问题提出方式，对养成学生发现和提出问题的意识起着有力的作用.

纵观以上案例，不难发现养成学生发现和提出问题的意识，并不像想象的那么困难.只要形成这样一种意识——根据教学内容挖掘与之相适合的背景，给学生创设观察的载体，把发现和提出问题的机会留给学生，并在日常的教学中持之以恒，学生经过日积月累，慢慢就会养成一种发现和提出问题的好习惯.如此，提高学生发现和提出问题的能力也就不会成为一句空话，有效地贯彻数学课标的总目标就能得以实现.

1．中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2．曾泽群.如何进行数学问题情境教学［M］.上海：华东师范大学出版社，2009.

3.曾大洋.如何上好一堂数学课［M］.上海：华东师范大学出版社，2009.H