图的无符号Laplace特征多项式的系数

邱玮（福州外语外贸学院　经济学院，福建　福州　350202）

图的无符号Laplace特征多项式的系数

邱玮
（福州外语外贸学院经济学院，福建福州350202）

摘要：我们考虑一般的连通图G的Laplace特征多项式f(G；x)与它的剖分图S(G)的特征多项式h(S(G)；x)之间会有什么关系，发现这两个多项式的系数是否以及何时存在差别，并刻画系数差的表达式．研究过程中，我们发现图G的无符号Laplace特征多项式g(G；x)是一个重要的桥梁．于是我们对其系数也进行研究，得到另一种新的方法证明图的无符号Laplace特征多项式系数的组合解释.

关键词：剖分图；一级半子图；Laplace特征多项式；无符号Laplace特征多项式

1　背景介绍

设G是b个顶点m条边的连通简单图，A（G)，B（G)和D （G)分别是G的邻接矩阵，关联矩阵和度对角矩阵，Q（G)=D （G)-A（G)是G的Laplace矩阵，Q（G)=D（G)+A（G)是G的无符号Laplace矩阵.

用f（G;x)表示图G的Laplace特征多项式，即

定理1.1[1，2]ai（G)=∑P（F)，i=0，1，…，n，这里求和取遍G的所有i条边的子森林F，其中P（F)表示F的每个分支的顶点数的乘积.

用g（G;x)表示图G的无符号Laplace特征多项式，即

给出图的TU-子图的定义：G的每个分支是树或者是非偶单圈图的生成子图称为G的TU-子图.

定理1.2[3]bi（G)=∑Φ（H)，i=0，1，…，n，这里求和取遍G的所有i条边的TU-子图H，其中Φ（H)=4'∏si=0ni，H有c=s+t个分支T1，T2，…，Ts，U1，U2，…，Ut，其中Ti（1≤i≤s)是ni个顶点的树，Uj（1≤j≤t)是非偶单圈图.

定理1.3[4]对任意n个顶点的连通图G，ai（G)≤bi（G)，i=0，1，…，n，等式成立当且仅当G是偶图.

设G1是G的一个子图，分别用r（G1)和s（G1)表示G1的秩和补秩，则有r（G1)=|V（G1)|-c（G1)，s（G1)=|E（G1)|-|V（G1)|+c（G1)，其中c（G1)是G1的连通分支数.

G的子图Λ称为G的一级半子图（elementary subgraph），如果Λ的每一个分支是一条边或者是一个圈.若Λ是G的一级半子图，则s（Λ)等于Λ的圈数.若H是G的TU-子图，则s（H)等于H的非偶单圈图的分支数.

用h（G;x)表示图G的特征多项式，即

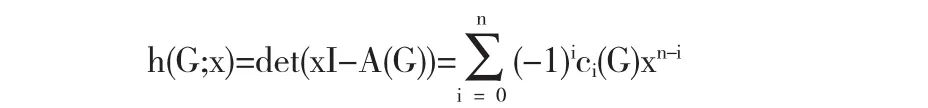
引理1.4[2]ci（G)=∑（-1)r（Λ)2s（Λ)，i=0，1，…，n，这里求和取遍G的所有i个顶点的一级半子图Λ.

图G的剖分图S（G)为在G的每条边e上插入一个新顶点所得到的图.关于偶图G的Laplace特征多项式与它的剖分图S（G)的特征多项式之间的关系，Zhou和Gutman得到了下面的结果：

定理1.5[5]设G是n个顶点m条边的偶图，S（G)是它的剖分图.则h（S（G);x)=xm-nf（G;x2).

2　定理1.2的证明

得S（G)的特征多项式为：

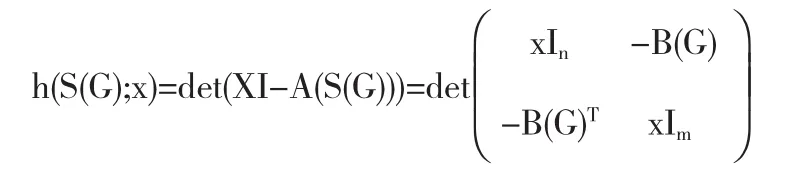
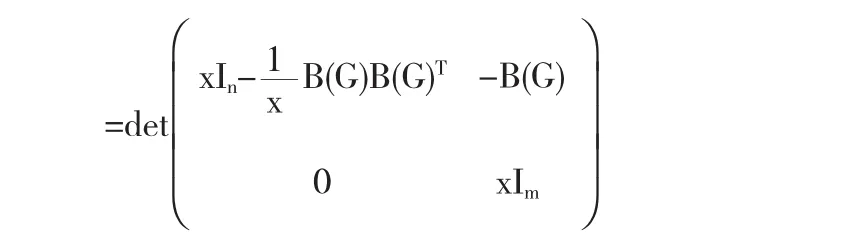
=xm-ndet（x2In-B（G)B（G)T)=xm-ndet（x2In-D（G)-A（G))

=xm-ng（G;x2)

注意到当G是偶图时，det（x2In-D（G)-A（G))=det（x2In-D（G) +A（G))，于是h（S（G);x)=xm-nf（G;x2).

现在设G是一般连通图，研究h（S（G);x)与f（G;x2)系数的关系，实际上就是发现f（G;x)系数ai（G)与g（G;x)系数bi（G)的差别.对于bi（G)，以下用一种新的方法来证明它的组合解释，即定理1.2内容.

我们发现

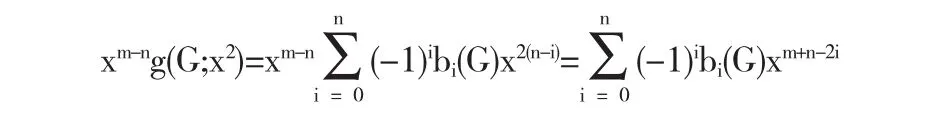
注意到S（G)没有奇圈，于是

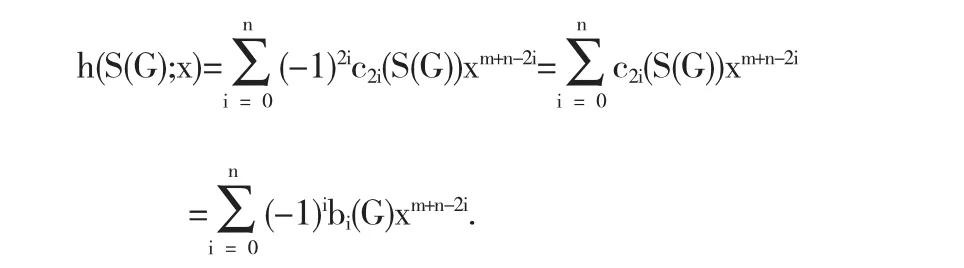
由引理1.4，得到下列引理.

引理2.1（-1)ibi（G)=c2i（S（G))=∑（-1)r（Λ)2s（Λ)，i=0，1，…，n，这里求和取遍S（G)的所有2i个顶点的一级半子图Λ.

为了阐明结论，先引入下面记号.

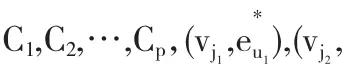
定义G的子图Λ'如下：收缩圈Ci的所有剖分点得到G的一个|V（Ci)|/2个顶点的圈，记为Ci'.设EΛ=E（C1')∪E（C2')∪…∪E（Cp')∪｛euk|k=1，2，…，q｝，则EΛ是G的边集E（G)的子集.定义Λ'是G的由EΛ导出的子图.设T1，T2，…，Ts，H1，H2，…，Ht是Λ'的分支，其中Tj（1≤j≤s)是树而Hj（1≤j≤t)至少包含一个圈.显然，|E（Tj)|≥1且|E（Hj)|≥3.

下面给出的结论是定理1.2证明的重要基础.

结论1 Λ'有i条边.

结论2 Λ是S（Λ')的一级半子图.特别地，Λ恰好含有S（Λ')中的i个v-型顶点和i个e-型顶点.

结论3 Λ'的每个分支或者是树或者是单圈图，即Hj（1≤j≤t)是单圈图.

由结论1和结论2，对于j=1，2，…，t，Λ恰好包含S（Hj)中的|E（Hj)|个v-型顶点和|E（Hj)|个e-型顶点.又因为|E（Hj)| ≤|V（Hj)|，于是|E（Hj)|=|V（Hj)|，即Hj（1≤j≤t)是单圈图.结论3成立.

再由结论3，每个Hj恰好包含一个圈.设Cj是S（Hj)的圈，那么Cj有两个完美匹配，记为M1（Cj)和M2（Cj).于是Cj恰有三组V（Cj)个顶点的一级半子图：M1（Cj)，M2（Cj)和Cj.不难说明S（Hj)-Cj恰有一个完美匹配，记为M（S（Hj)-Cj).这意味着下面结论.

结论4对于1≤j≤t，S（Hj)恰有三组V（S（Hj))个顶点的一级半子图：M1（Cj)∪M（S（Hj)-Cj)，M2（Cj)∪M（S（Hj)-Cj)和Cj∪M （S（Hj)-Cj).

结论5设Λ1是S（Λ')的2i个顶点的一级半子图.则Λ1可表示成M1∪M2∪…∪Ms∪M'1∪M'2∪…∪M't的形式，其中Mj（1≤j≤s)是S（Tj)的|E（Tj)|条边的匹配，而M'j（1≤j≤t)是S（Hj)的V（S（Hj))个顶点的一级半子图.

引理2.2[6]设T是树，则它的剖分图S（T)有|V（T)|个|E （T)|条边的匹配.

由结论5和引理2.2，我们得到

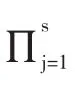
结论7对任意Λk∈Γ（Λ')，Λk'=Λ'.

引理2.3设T1，T2，…，Ts，H1，H2，…，Ht是Λ'的分支，其中Tj（1≤j≤s)是树，Hj（1≤j≤t)是单圈图.假设H1，…，Hx是非偶单圈图而Hx，…，Hx+y（x+y=t)是偶单圈图，则

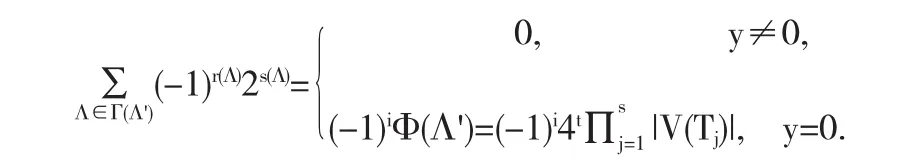
证明设Cj（1≤j≤t)是S（Hj)的圈.那么当1≤j≤x时，|V （Cj)|=2（mod4)，而当x+1≤j≤x+y=t时，|V（Cj)|=0（mod4).注意到Γ（Λ')是S（Λ')的2i个顶点的一级半子图的集合，且它们都能被看成是S（G)的2i个顶点的一级半子图.

记

M'j1=M1（Cj)∪M（S（Hj)-Cj)，M'j2=M2（Cj)∪M（S（Hj)-Cj)，

M'j3=Cj∪M（S（Hj)-Cj).

对于1≤kj≤3，j=1，2，…，t，定义Γk1k2…kt（Λ')是其元素形如M1∪M2∪…∪Ms∪M'1k1∪M'2k2，∪…∪M'tkt的集合，显然有下列结论.

（2）若（k1，k2，…，kt)≠（l1，l2，…，lt)（kj，lj=1，2，3，1≤j≤t)，则Γ

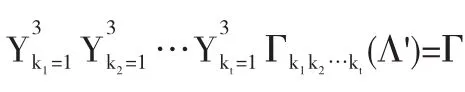
（3）设Λ=M1∪M2∪…∪Ms∪M'1k1∪M'2k2，∪…∪M'tkt∈Γk1k2…kt（Λ').

如果在集合{k1，k2，…，kx}（{kx+1，kx+2，…，kt})中恰有x1（y1）个元素等于3，则Λ的分支数

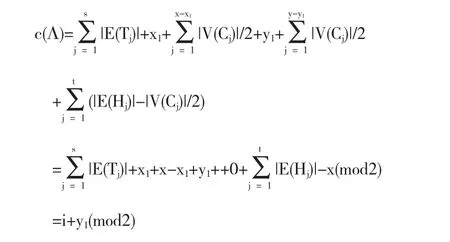
所以（-1)r（Λ)2s（Λ)=（-1)c（Λ)2x1+y1=（-1)i+y12x1+y1.再由（1），（2）和（3）

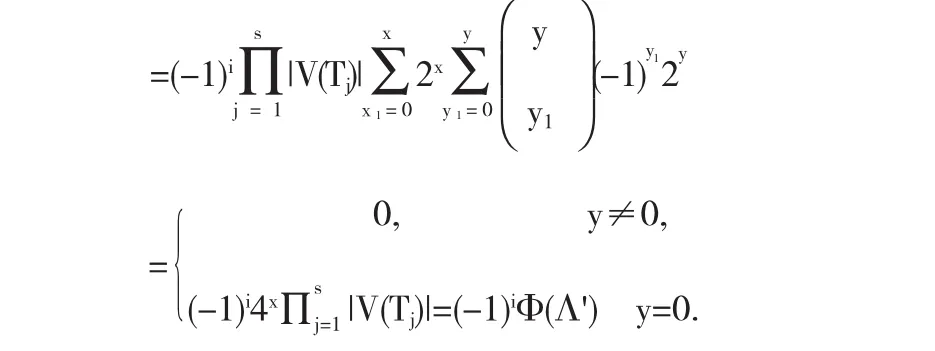
定理1.2的新的证明：设Γ'（G)={Λ'1，Λ'2，…，Λ'ω}是G的i条边的每个分支是树或单圈图的子图的集合.再设Γ（Λ'j) （j=1，2，…，ω)是S（Λj)的2i个顶点的一级半子图的集合，它们都可以看成是S（G)的一级半子图.不难发现Γ（Λ'j)∩Γ（Λ'k)=ø，1≤j≠k≤ω.此外，Γ（Λ'1)∪Γ（Λ'2)∪…∪Γ（Λ'ω)=Γ是S（G)的全体2i个顶点的一级半子图集合.由引理2.1，

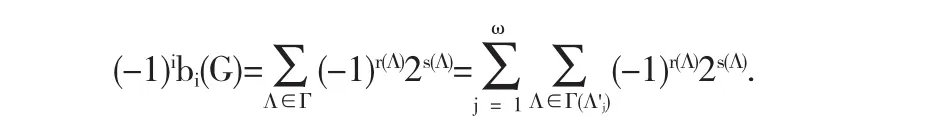
参考文献：

〔1〕A．K．Kel’mans，V．M．Chelnokov．A certain polynomial of a graph and graphs with an extremal number of trees[J]．J．Combin．Theory，Ser．B，1974，16：197－214．Erratum [J]．J．Combin．Theory，Ser．B，1978，24：375．

〔2〕N．L．Biggs．Algebraic Graph Theory [M]．Cambridge：Cambridge University Press，1993．

〔3〕D．Cvetkovi？，P．Rowlinson，S．K．Simi？．Signless Laplacians of finite graphs [J]．Linear Algebra and its Applications，2007，423：155－171．

〔4〕S．Akbari，E．Ghorbani，J．H．Koolen，M．R．Oboudi．A relation between the Laplacians and signless Laplacians eigenvalues of graph[J]．Alg．Combin．，2010，32：459－464．

〔5〕B．Zhou，I．Gutman．A connection between ordinary and Laplacians spectra of bipartite graphs [J]．Linear and Multilinear Algebra，2008，56：305－310．

〔6〕W．G．Yan，Y．-N．Yeh．Connections between Wiener index and matchings[J]．Math．Chem．，2006，39：389－399．

中图分类号：O157.5

文献标识码：A

文章编号：1673-260X（2015）09-0007-03