一种重力测量卫星质心在轨标定改进算法
辛宁 邱乐德 张立华 刘乃金
(1 中国空间技术研究院通信卫星事业部, 北京 100094) (2 航天东方红卫星有限公司, 北京 100094)
一种重力测量卫星质心在轨标定改进算法
辛宁1邱乐德1张立华2刘乃金1
(1 中国空间技术研究院通信卫星事业部, 北京 100094) (2 航天东方红卫星有限公司, 北京 100094)
针对重力测量卫星质心在轨标定算法中存在的陀螺精度不高且易失效的问题,提出了一种应用星敏感器和静电加速度计的质心标定改进算法。在该算法中,将一个明显大于干扰力矩的周期性磁力矩,作用于卫星上;将星敏感器观测量代入预测滤波器中,估计卫星的角速度及角加速度;利用静电加速度计信息设计扩展卡尔曼滤波,从而实现卫星质心的标定。数学仿真结果表明:此算法能够对卫星的角速度及质心位置进行实时估计,卫星质心三轴最佳标定精度均优于0.05 mm,可实现陀螺失效情况下卫星质心较为精确的标定。
重力测量卫星;质心在轨标定;预测滤波;扩展卡尔曼滤波;星敏感器
1 引言
为得到高精度的地球重力场数据,重力测量卫星要利用静电加速度计测量非重力因素对卫星轨道的影响[1]。静电加速度计中检验质量块的质心与卫星质心的位置偏差,将直接影响非重力因素的测量精度。产生上述偏差的主要因素包括:地面卫星质心校准存在的误差;卫星质量的损失,如卫星在轨飞行中燃料的消耗,卫星在空间真空电离环境中长期运行时部分物质的蒸发等;其他因素的影响,如卫星发射段振动[2]。因此,开展卫星质心的在轨标定算法研究,为质心在轨修正任务提供依据,具有重要的意义[3]。
目前,重力测量卫星质心的在轨标定算法,必须利用陀螺来获取卫星的角速度信息,且存在一定的局限性。陀螺的误差漂移特性会使测量精度降低,而且陀螺有可能失效,从而导致质心在轨标定算法无法应用。文献[4]中详细介绍了“重力校正和气候实验”(GRACE)卫星的质心在轨标定算法,该算法除了需要陀螺的角速度数据外,还要精确已知控制输入以及卫星姿态动力学特性,这些参数在质心标定期间往往存在不确定性。文献[5]中提出将陀螺数据代入最小模型误差估计算法中估计卫星角加速度,利用扩展卡尔曼滤波估计卫星质心。最小模型误差估计算法是一种离线估计算法,因此无法对质心位置进行实时估计。为了提高重力测量卫星质心在轨标定算法的可靠性,避免陀螺的不利影响,本文在目前已有研究的基础上,提出了一种应用高精度星敏感器和静电加速度计的质心标定改进算法,在保证质心标定精度的同时,可为重力测量卫星设计提供一种新的解决方案。
本文提出的质心标定改进算法,首先利用高精度星敏感器,结合非线性预测滤波估计卫星的角速度及角加速度;然后通过扩展卡尔曼滤波估计实现卫星质心的在轨标定。该算法中的滤波器不需要卫星的控制输入以及动力学特性信息,能够实时估计卫星质心、角速度及角加速度,具有快速的收敛性能和良好的稳定精度,可实现无陀螺条件下的卫星质心在轨标定。
2 卫星质心在轨标定改进算法
重力测量卫星质心在轨标定改进算法的基本原理如图1所示。根据地球磁场模型及卫星的轨道位置,给卫星施加一定频率的磁力矩,使卫星产生相应的转动;将静电加速度计、星敏感器作为检测传感器,对星敏感器观测矢量进行预测滤波处理,估计出角速度及角加速度;对静电加速度计观测矢量进行扩展卡尔曼滤波处理,分离出具有线性特征的非重力加速度分量,由此来确定卫星质心的位置。
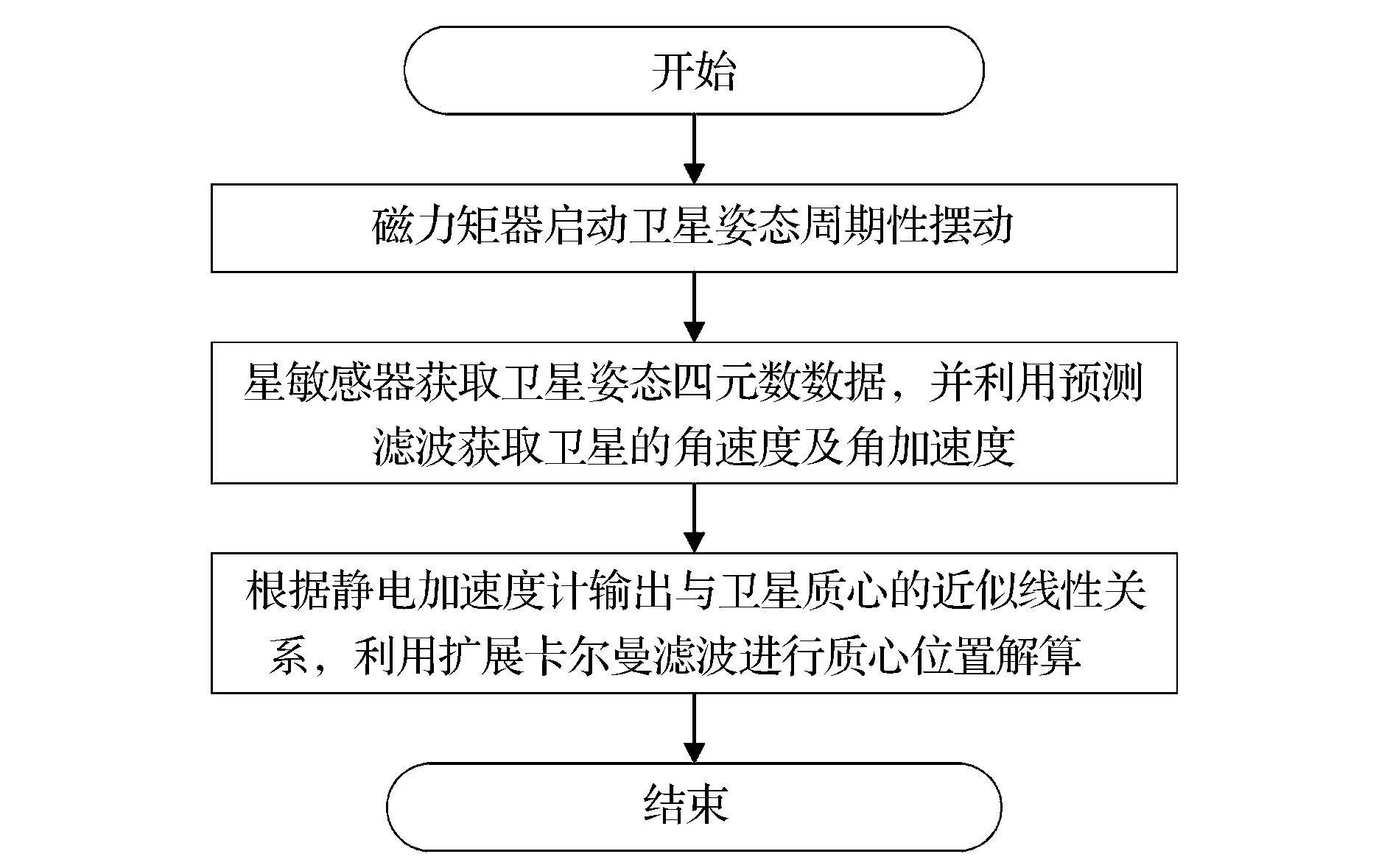
图1 卫星质心在轨标定流程Fig.1 Flow of on-orbit calibration of satellite center of mass
2.1 系统模型
重力测量卫星本体坐标系与静电加速度计坐标系的关系如图2所示,卫星本体坐标系的原点OS1为卫星质心,XS1轴垂直于卫星轨道平面,YS1轴表示卫星飞行方向,ZS1轴表示卫星对地指向。静电加速度计坐标系的原点为检验质量块质心位置OA1,理论上与OS1重合,YA1轴和ZA1轴分别平行于卫星本体坐标系的ZS1轴和XS1轴。
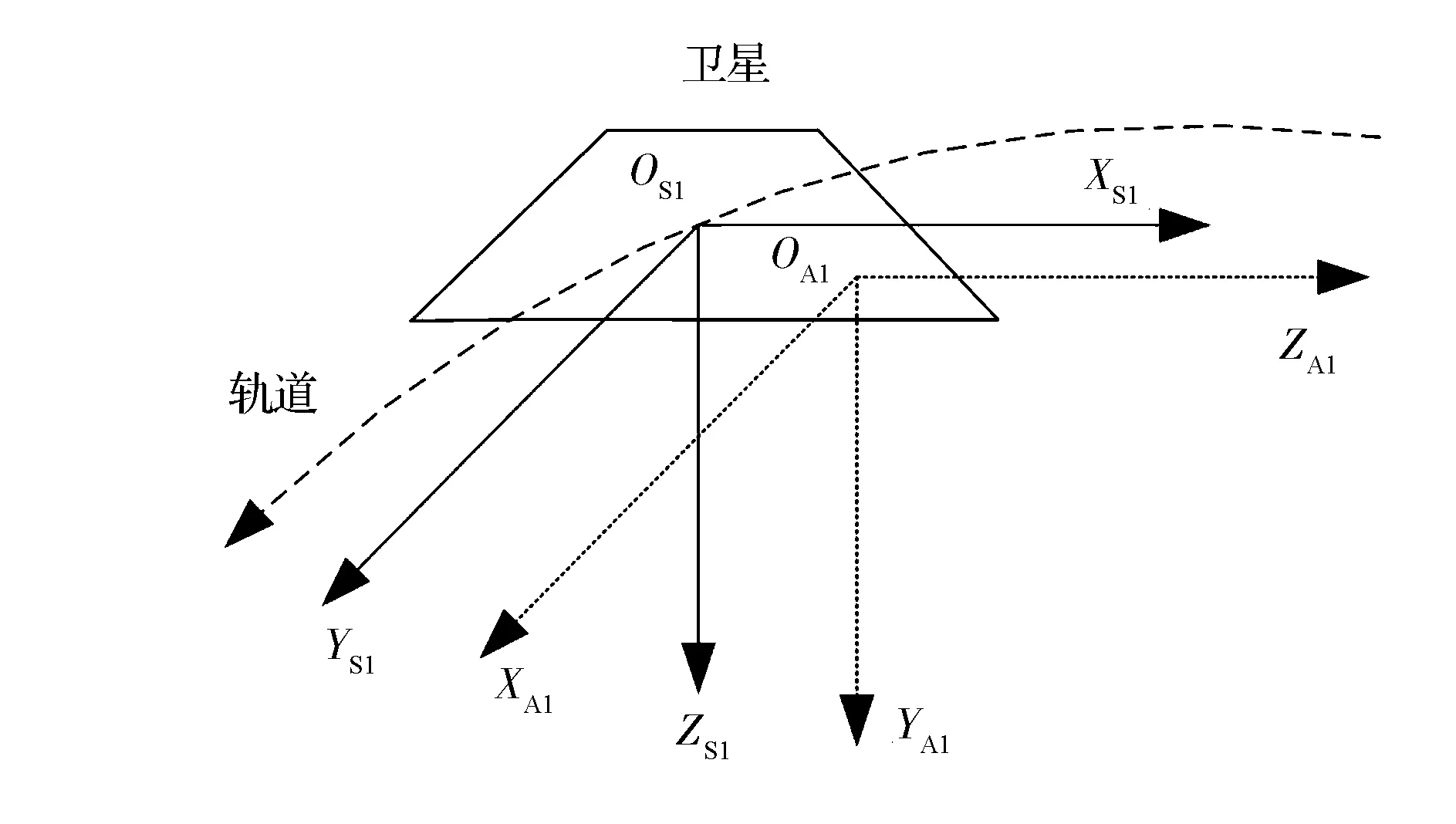
图2 卫星本体坐标系与静电加速度计坐标系Fig.2 Satellite body-fixed coordinate system and electrostatic accelerometer coordinate system
静电加速度计在卫星本体坐标系下输出的非保守力可表示为[6]
Fobs=MAB(s1Fout)+Ab+An
(1)
式中:MAB为静电加速度计坐标系到卫星本体坐标系的转换矩阵;s1为静电加速度计的标度因子;Fout为静电加速度计在静电加速度计坐标系下的实际输出,见式(2);Ab为零偏误差;An为噪声误差。
(2)
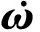
由文献[6]中可知,由重力梯度和非保守力因素引起的加速度分量,在较短的标定时间t内基本保持线性关系,因此质心在轨标定的测量方程为
(3)
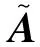
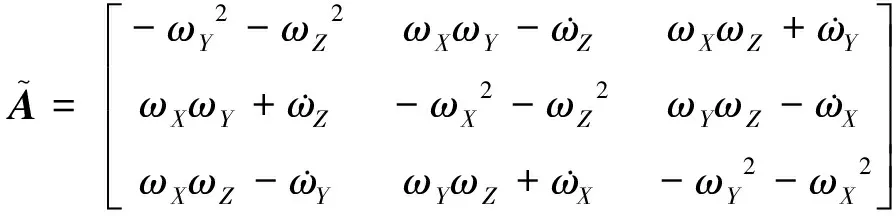
(4)
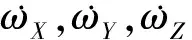
显然,在构建上述测量方程时,必须要利用卫星的角速度和角加速度信息。由于陀螺精度不高,难以准确获取角速度及角加速度信息,这成为重力测量卫星质心在轨标定的一个难点。为此,本文将星敏感器测量的卫星姿态四元数代入到预测滤波中,以精确地获取卫星角速度及角加速度信息;再利用扩展卡尔曼滤波对质心位置进行标定。
2.2 角速度预测滤波估计
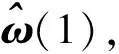
(5)
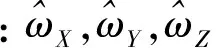
(2)求取正弦基模参数S(i)。
(6)
(3)利用正弦基模参数S(i)和时间序列i的载体姿态四元数q(i+1),可以求得i+1时的转换矩阵Tq,ω(i+1)。
(7)
式中:q0,q1,q2,q3为姿态四元数q的4个分量。
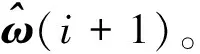
(8)
式中:Nu为由姿态四元数q的标部产生的标部值。
由式(7)和式(8)可得角速度估计值的状态方程为
(9)
式中:d(i)为模型误差;I为单位向量。
使用四元数表示的卫星姿态运动微分方程为
(10)
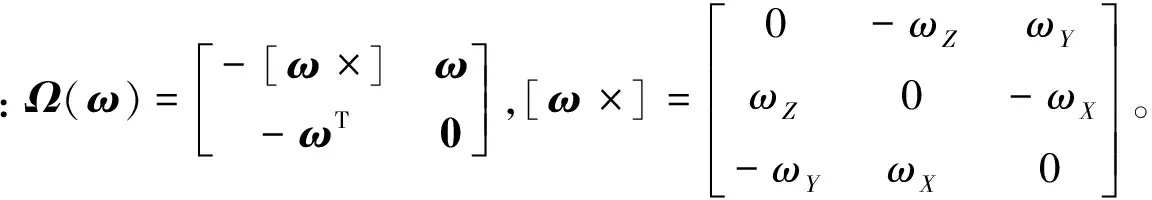
将式(10)表示为离散形式,根据四元数定义可得角速度估计值的观测方程为
q(i)=
q(i-1)+v(i)
(11)
式中:v(i)为零均值高斯白噪声。
预测滤波的物理概念[7]是:设已经获得了i时的状态估计值,采样间隔时间为Δi,在接到i+Δi时的测量信息q(i+1)后,利用模型最小误差逼近可预测[i,i+Δi]范围内的模型误差d1(i),然后将d1(i)的预测值代入系统状态方程和观测输出方程中,将状态估计值传播到i+1时,从而得到较高的估计精度。
为了估计出模型误差,首先将q(i+1)采用泰勒级数法展开,直到模型误差d1(i)出现,有
q(i)+y(i)+Λ(Δi)S(i)d1(i)
(12)
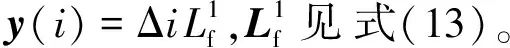
(13)
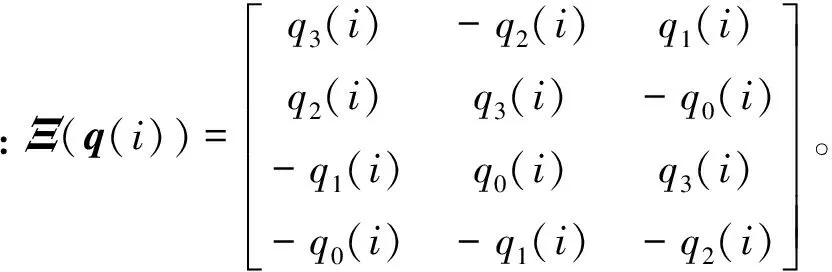
根据预测滤波理论,由式(12)可得
d1(i)=-{[Λ(Δi)S(i)]TR-1[Λ(Δi)S(i)]+W}-1·
[Λ(Δi)S(i)]TR-1[y(i)-q(i+1)+q(i)]
(14)
式中:W为3×3阶加权矩阵;R为量测噪声协方差矩阵。
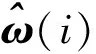
上述过程的实质是先预测下一时刻的模型误差校正量,然后再对状态估计值进行误差修正,从而有效地提高了角速度的估计精度。
2.3 角加速度预测滤波估计
卫星角加速度的表达式为
(15)
式中:Jp为卫星转动惯量;M为卫星力矩。
将式(15)等号右边的状态信息全部定义为模型误差d2(i),由此获得的角加速度的系统状态方程和观测方程为
(16)
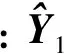
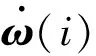
2.4 质心的扩展卡尔曼滤波估计
在卫星角速度及角加速度估计值已知的条件下,质心估计参数X=[lαβ]T,进行估计的系统状态方程及观测方程为
(17)
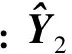
待估状态变量一步预测估计均值为
(18)
式中:k为时间序列标志符;状态转移矩阵Φ(tk)=I9×9。
一步估计均方误差矩阵为
P(tk+1/k)=Φ(tk)P(tk)ΦT(tk)
(19)
反馈增益矩阵为
K(tk+1)=P(tk+1/k)HT(tk+1)·
[H(tk+1)P(tk+1/k)H(tk+1)+Q(tk+1)]-1
(20)
估计均方误差矩阵为
P(tk+1)=[I-K(tk+1)H(tk+1)]P(tk+1/k)
(21)
状态估计值为
X(tk+1)=X(tk+1/k)+K(tk+1)·
(22)
3 仿真实例
3.1 仿真条件
重力测量卫星质心在轨标定改进算法的数学仿真参数,如表1所示。
为了使卫星质心在轨标定改进算法能够得到合适的精度,分别在俯仰、偏航和滚动方向施加周期性的磁偶极矩Mm=30sin(0.2πt)A·m2,为了检验所设计的磁偶极矩信号的持续时间与质心标定精度的关系,将信号的时间间隔分别设定为100s,200s,300s,400s。为了分析得到数据采集的轨道相位与质心标定精度的关系,分别选在赤道附近及南极附近进行卫星质心在轨标定。
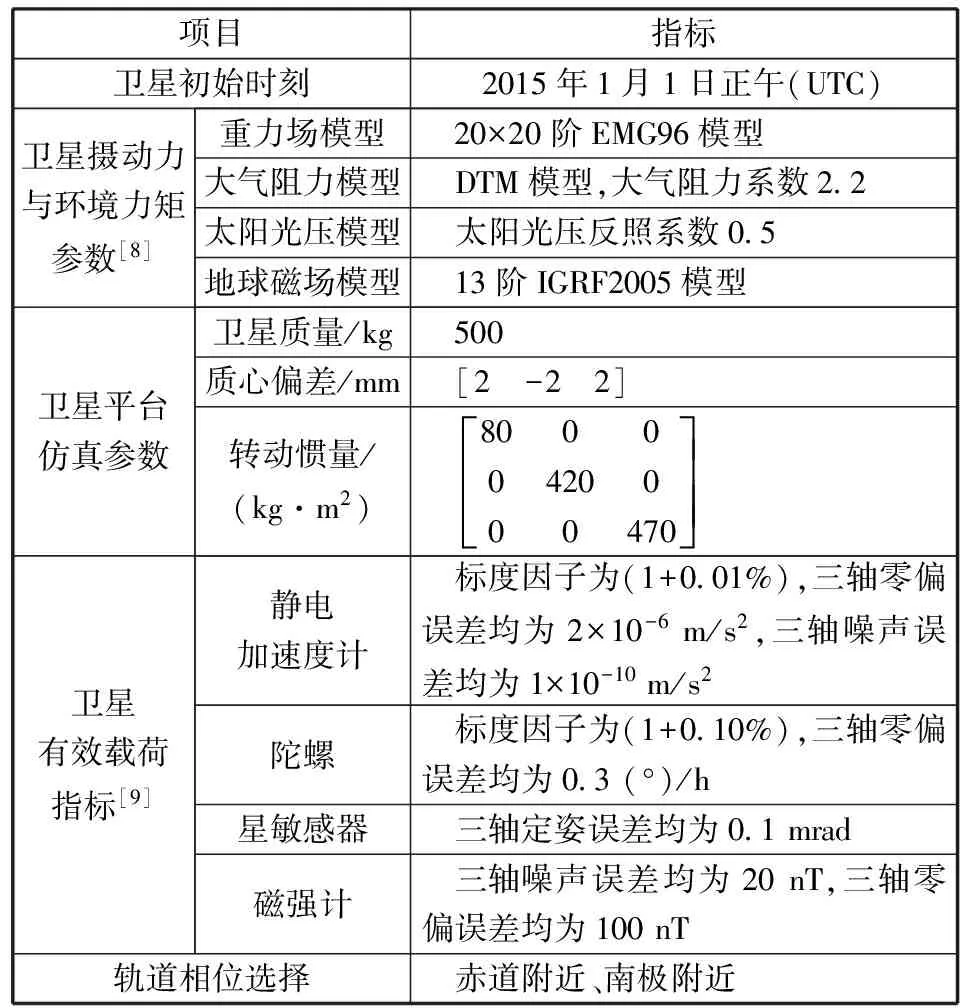
表1 仿真参数
3.2 仿真流程
卫星质心在轨标定改进算法仿真流程见图3。具体步骤为:①当卫星运行到地球赤道上空时,将磁力矩器作为姿态控制元件,分别在俯仰、偏航、滚动方向产生较大的周期性磁偶极矩,获得的磁力矩作用于卫星上,使卫星进行姿态机动,姿态机动完成后恢复正常工作姿态;②将姿态机动过程中星敏感器输出的姿态四元数进行基于预测滤波的四元数-角速度算法解算,获得卫星的角速度;③根据解算的角速度,采用预测滤波解算出卫星的角加速度;④利用静电加速度计数据与卫星质心位置的线性关系,带入卫星的角速度、角加速度,采用扩展卡尔曼滤波进行解算,即可获得卫星质心在卫星本体坐标系下的位置。
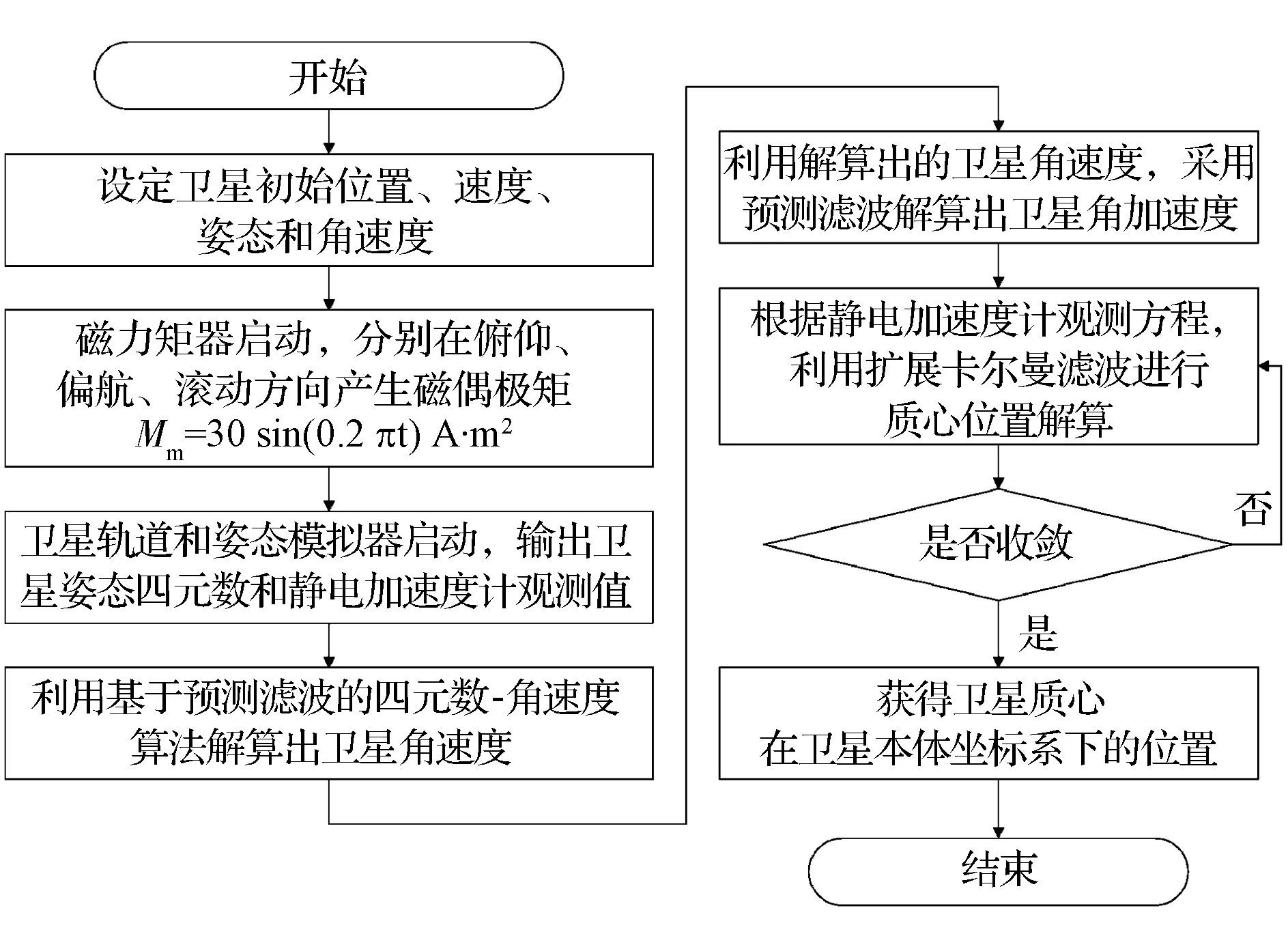
图3 仿真流程Fig.3 Simulation flow
3.3 数值仿真结果
在赤道上空进行姿态机动,在卫星滚动(X轴)、俯仰(Y轴)和偏航(Z轴)方向上的磁偶极矩如图4所示。磁偶极矩是幅度为30 A·m2、频率为0.1 Hz的正弦波,机动总时间为300 s,间隔为100 s。图5为卫星的磁力矩,三轴的磁力矩最大幅值分别为0.4 mN·m,0.75 mN·m,0.75 mN·m,形式仍为正弦波,频率仍为0.1 Hz。采用基于预测滤波的四元数-角速度算法,得到的卫星角速度估计值如图6所示,可以看出,基于预测滤波的四元数-角速度算法具有很好的鲁棒性。三轴角速度估计误差的平均值低于3×10-8rad/s,标准差低于5×10-7rad/s,具有很好的估计精度,作为参考角速度完全符合要求。卫星角加速度估计值如图7所示。改进算法将全部状态信息定义为模型误差,仅利用量测信息便能精确地估计出卫星质心标定期间的角加速度。静电加速度计的输出结果如图8所示,X轴方向的线性加速度近似效果相对较差,主要原因是X轴方向为卫星的飞行方向,大气阻力在此方向上的量级远远大于其他两个方向。
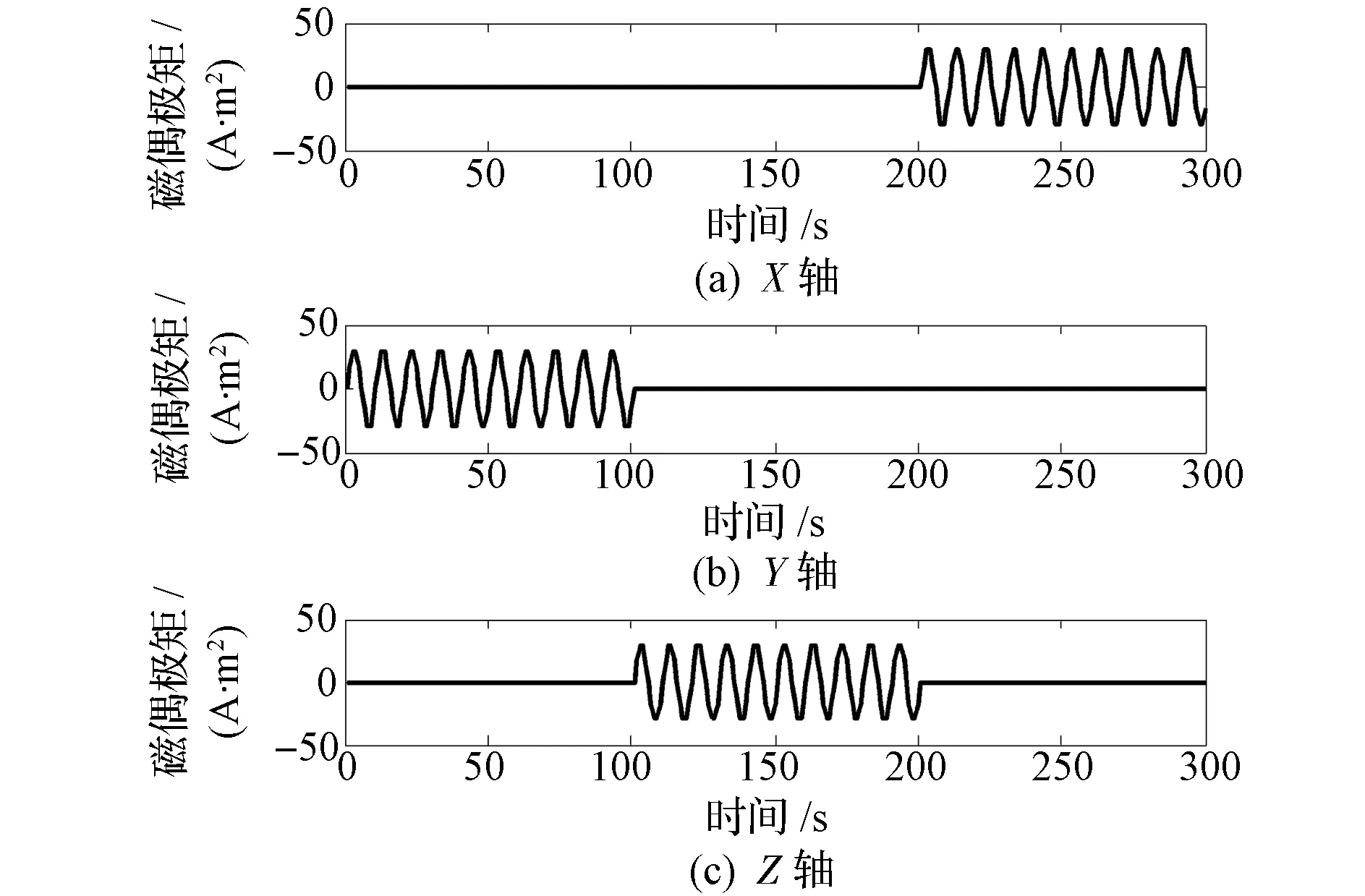
图4 赤道上空时卫星的磁偶极矩Fig.4 Satellite magnetic dipole moment over equator
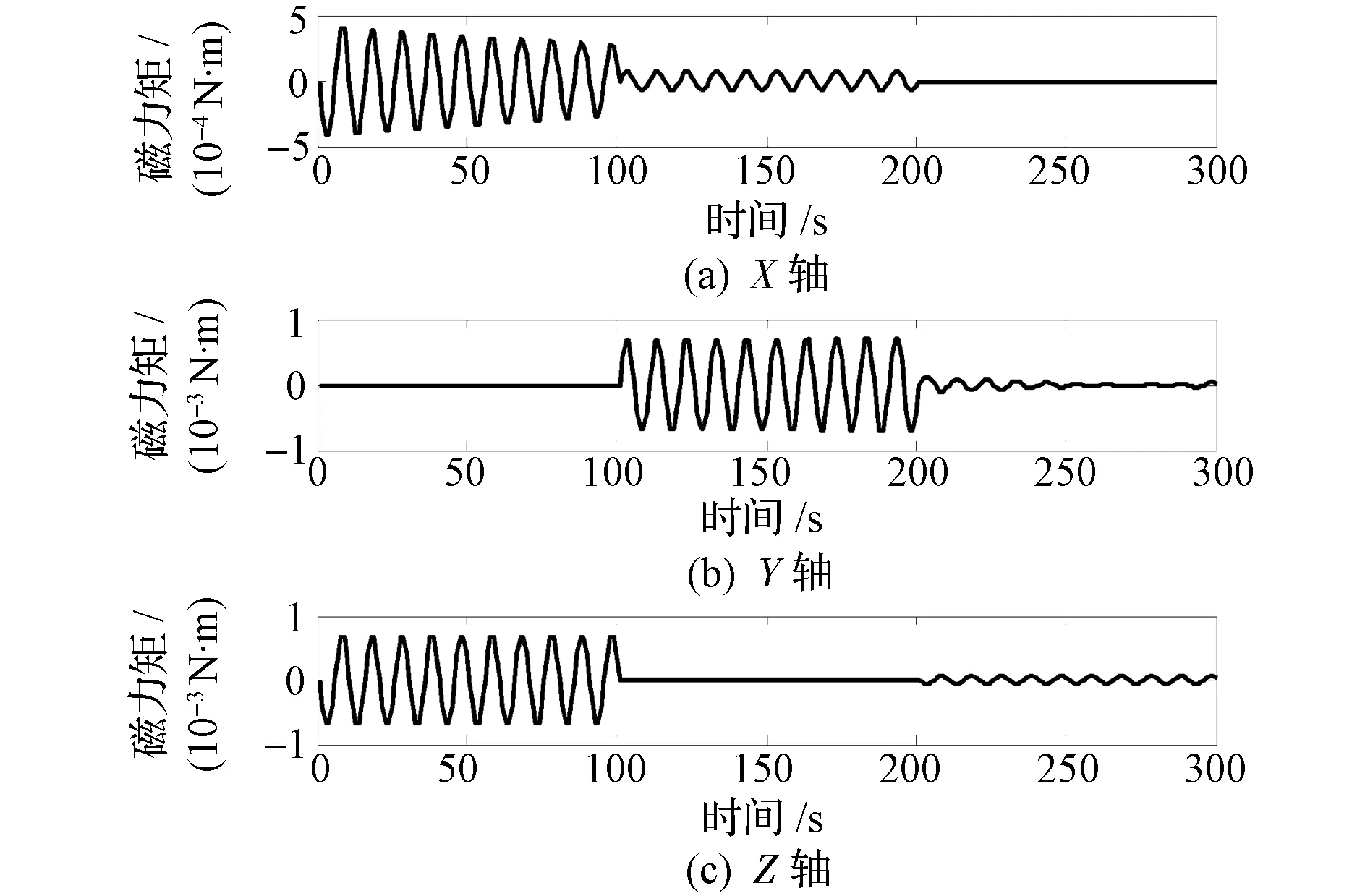
图5 赤道上空时卫星的磁力矩Fig.5 Satellite magnetic torque over equator
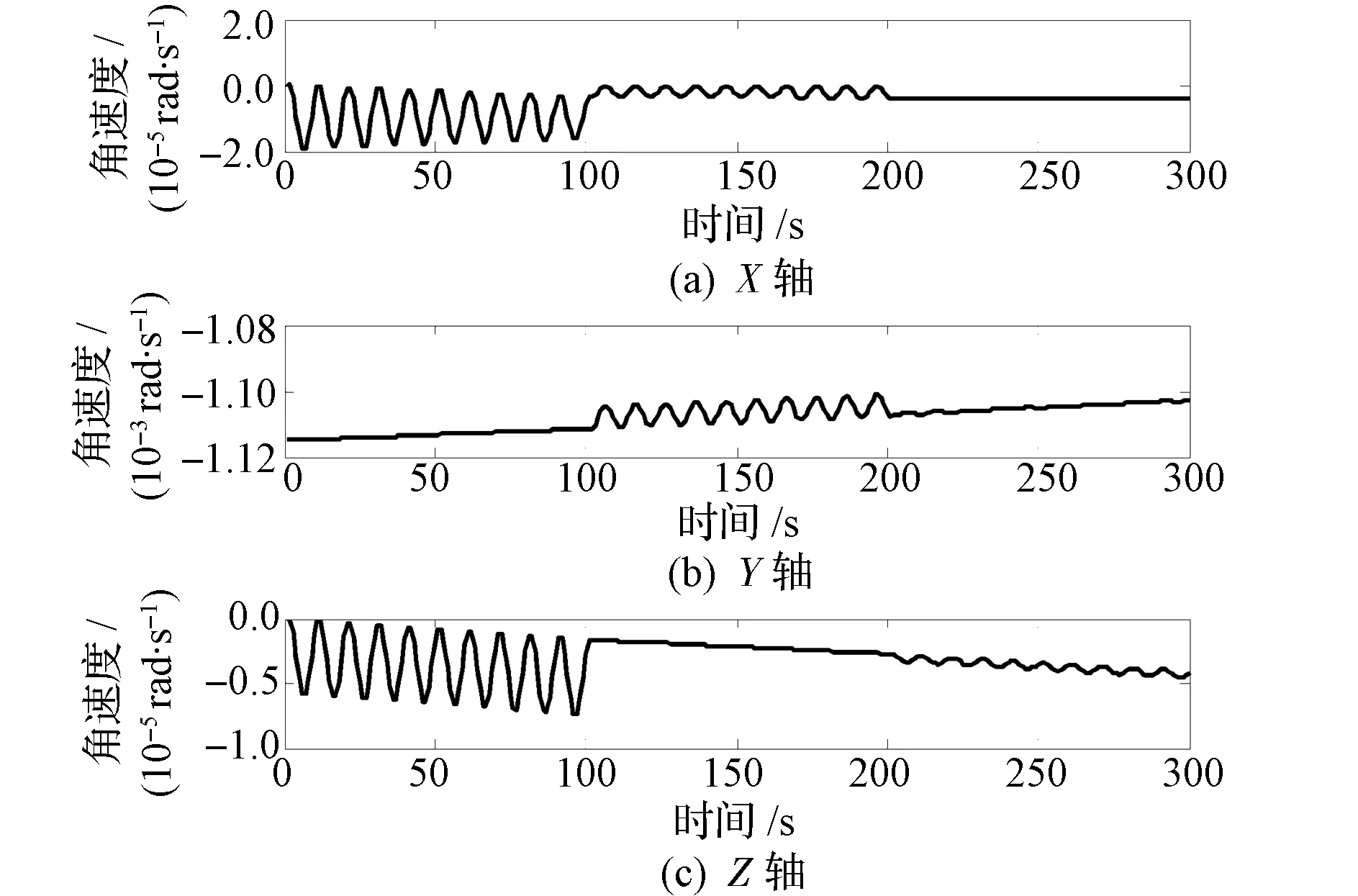
图6 赤道上空时卫星的角速度估计值Fig.6 Estimation of angular rate over equator
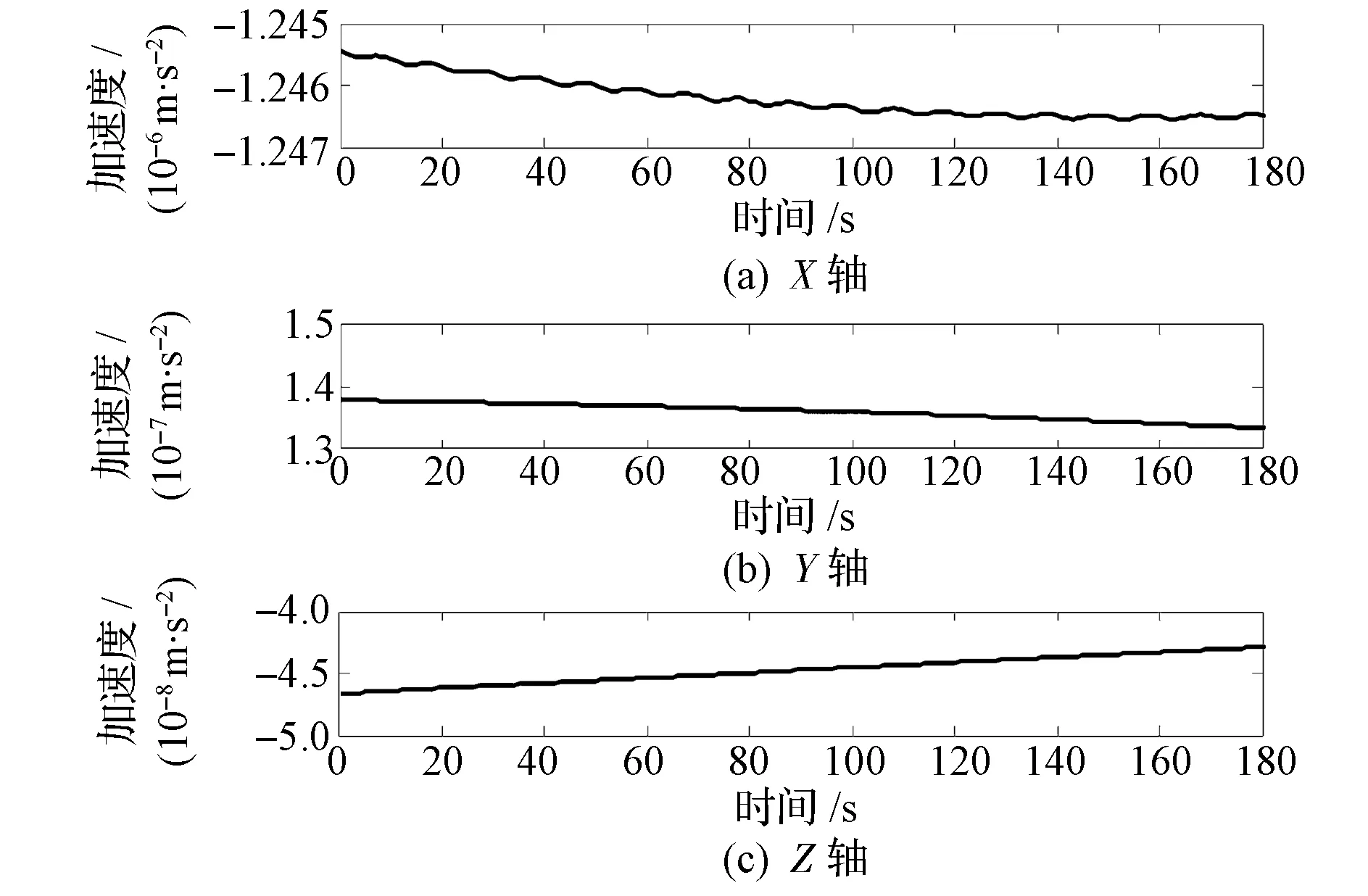
图8 赤道上空时静电加速度计的输出Fig.8 Electrostatic accelerometer output over equator
卫星质心在轨标定精度如表2所示,根据美国GRACE卫星的指标,质心三轴标定精度须在0.05 mm以内[8]。
由表2可以看出,X轴、Y轴和Z轴的最佳标定精度分别为0.022 mm,0.005 mm,0.008 mm。因此,本文提出的质心标定改进算法满足标定精度需求。在相同条件下,在赤道上空进行姿态机动,质心标定结果要略优于在南极上空机动的结果。其主要原因是:赤道上空激励起的三轴角加速度较为均匀,这样利于质心标定精度的提高;而南极上空激励的三轴角加速度幅值差异较大。通过不同的激励时长看,300~900 s的总机动时间是可以接受的,如果激励时间再长,质心测量精度反而降低。这是因为:标定中假设的非重力加速度项在质心标定期间保持线性关系,而随着标定时间的延长,这种假设的误差越来越大,反而不利于质心标定精度的提高。
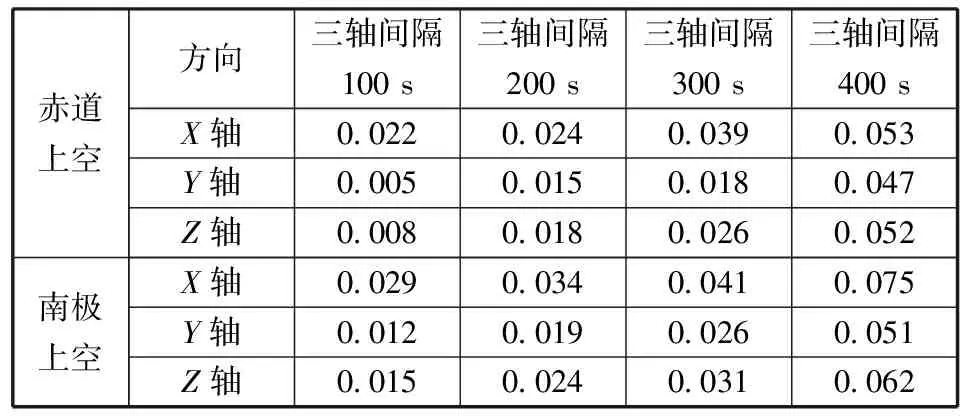
表2 卫星质心在轨标定精度
4 结束语
重力测量卫星质心在轨标定的核心问题是,在缺乏直接敏感元件的情况下,如何高精度地确定卫星角速度及角加速度信息。针对这一问题,本文提出了一种预测滤波与扩展卡尔曼滤波相结合的质心在轨标定改进算法。该算法通过设计估计角速度及角加速度的预测滤波与质心的扩展卡尔曼滤波,实现卫星质心的标定,模型结构比较简单,且利用非线性预测滤波建模非常方便。仿真结果表明:在不使用陀螺或者陀螺失效的情况下,卫星质心在轨标定仍具有较高的精度,因而改进算法为重力测量卫星质心在轨标定提供了一种新的解决思路。
References)
[1]周泽兵,白彦峥,祝竺,等. 卫星重力测量中加速度计在轨参数校准方法研究[J].中国空间科学技术,2009,29(6):74-80
Zhou Zebing,Bai Yanzheng,Zhu Zhu,et al. In-orbit cali-bration methods of accelerometer parameters on satellite-borne gravimetry [J]. Chinese Space Science and Technology,2009,29(6):74-80 (in Chinese)
[2]佘世刚,王锴,周毅,等. 高精度星间微波测距技术[J].宇航学报,2006,27(3):403-406
She Shigang, Wang Kai,Zhou Yi,et al. The technology of high accuracy inter-satellite microwave ranging [J]. Journal of Astronautics, 2006,27(3):403-406 (in Chinese)
[3]陈光锋,唐富荣,薛大同.重力卫星在轨质心修正原理[J].宇航学报,2005,26(5):567-570
Chen Guangfeng,Tang Furong,Xue Datong. The trim principle of center of mass of gravity satellite during orbit flight [J]. Journal of Astronautics,2005,26(5):567-570 (in Chinese)
[4]Wang F, Tapley B D. Precise determination of accelero-meter proof mass [C]//Proceedings of AAS/AIAA Space Flight Mechanics Meeting. Washington D.C.:AIAA,2002:739-752
[5]王本利,廖鹤,韩毅. 基于MME/EKF算法的卫星质心在轨标定[J].宇航学报,2010,31(9): 2150-2156
Wang Benli, Liao He, Han Yi. On-orbit calibration of satellite center of mass based on MME/EKF algorithm [J]. Journal of Astronautics,2010,31(9):2150-2156 (in Chinese)
[6]Tangyin S, Williams T. Mass property estimation using coasting maneuvers [J]. Journal of Guidance, Control and Dynamic, 1997,20(4):625-632
[7]Crassidis J L. Predictive filtering for attitude estimation without rate sensors [J]. Journal of Guidance, Control and Dynamic, 1997,20(3):522-527
[8]Kim J R. Simulation study of a low-low satellite-to-satellite tracking mission [D].Austin: University of Texas at Austin, 2000
[9]Furun Wang. Study on center of mass calibration and K-band ranging system calibration of the GRACE mission [D]. Austin: University of Texas at Austin, 2003
(编辑:夏光)
An Improved Algorithm for On-orbit Calibration of Gravity Measurement Satellite Center of Mass
XIN Ning1QIU Lede1ZHANG Lihua2LIU Naijin1
(1 Institute of Telecommunication Satellite, China Academy of Space Technology, Beijing 100094, China) (2 DFH Satellite Co. Ltd., Beijing 100094, China)
In view of low precision and vulnerability of gyros, an improved algorithm for on-orbit calibration of gravity measurement satellite center of mass based on star sensor and electrostatic accelerometer is proposed.A periodic magnetic torque which is larger than other external torques is applied on satellite.The observation of star sensor is used to estimate angular rate and acceleration based on predictive filter.The extended Kalman filter is used to estimate the center of mass of satellite by using electrostatic accelerometer data.The numerical simulation results indicate that the angular acceleration and center of mass can be real-time estimated synchronously, and the calibration accuracy of three axes is better than 0.05mm, which can demonstrate the effectiveness of the proposed algorithm even without gyros.
gravity measurement satellite; on-orbit calibration of center of mass; predictive filter; extended Kalman filter; star sensor
2014-11-14;
2015-01-28
国家自然科学基金(91438205)
辛宁,男,博士,研究方向为卫星系统总体设计。Email:xinning7@sina.com。
P228
A
10.3969/j.issn.1673-8748.2015.04.008

