星载微波辐射计的线性与非线性反演算法比较

王兆徽 刘宇昕，2 宋清涛,2 吴彬锋

(1 国家卫星海洋应用中心, 北京 100081) (2 国家海洋局空间海洋遥感与应用研究重点实验室, 北京 100081)



星载微波辐射计的线性与非线性反演算法比较

王兆徽1刘宇昕1，2宋清涛1,2吴彬锋1

(1 国家卫星海洋应用中心, 北京 100081) (2 国家海洋局空间海洋遥感与应用研究重点实验室, 北京 100081)

针对星载微波辐射计反演海洋大气参数的过程，分析了反演通道的选择，比较了线性与非线性反演算法的区别。非线性反演算法逐步舍去低分辨率的低频通道，能够直接有效地提高反演产品的空间分辨率。对几种反演算法的分析和实验表明，非线性反演算法中的基于Nelder-Mead的最优化反演算法相对于线性反演算法，其精度较高，具有一定的开发价值和应用潜力。

星载微波辐射计； 反演算法； Nelder-Mead算法

1 引言

星载微波辐射计是测量地表或大气通过热辐射辐射出的电磁波的仪器，其应用始于1962年美国发射的水手2号(Mariner-2)卫星进行金星飞行探测。从1972年开始，微波辐射计应用于海洋方面的研究。美国1972年发射的雨云5号(Nimbus-5)卫星和1975年发射的雨云6号(Nimbus-6)卫星搭载了单通道电磁扫描微波辐射计(Electrically Scanning Microwave Radiometer，ESMR)，验证了被动微波遥感反演海洋大气参数的潜力。1978年发射的雨云7号(Nimbus-7)卫星搭载了采用扇形机械扫描方式的扫描多通道微波辐射计(Scanning Multichannel Microwave Radiometer，SMMR)。1987年之后国防气象卫星计划(Defense Meteorological Satellite Program，DMSP)搭载了专用遥感器微波成像仪(Special Sensor Microwave/Image，SSM/I)。SSM/I改进了SMMR的许多仪器硬件问题，并为后续的“热带降雨测量任务”(Tropical Rainfall Measuring Mission，TRMM)卫星搭载的热带微波成像仪(Tropical Microwave Imager,TMI)和先进微波扫描辐射计(Advanced Microwave Scanning Radiometer,AMSR)的设计提供了基础。AMSR[1]是日本宇宙航空研究开发机构(JAXA)和美国航空航天局(NASA)联合设计发射的星载微波扫描辐射计。包括搭载于地球观测-水(EOS-Aqua)卫星的AMSR-E，搭载于日本先进地球观测卫星-2(ADEOS-II)的AMSR，以及搭载于全球环境变化观测-W1(GCOM-W1)卫星的AMSR-2。

中国的“风云”系列卫星和“海洋”系列卫星均搭载了微波辐射计。2000年6月25日发射的风云二号(FY-2B)是静止轨道气象卫星，搭载了3通道的微波辐射计。风云二号的后续卫星和风云三号都[2]增设了微波辐射计的通道数目。中国于2011年8月发射了首颗海洋动力环境卫星——海洋二号(HY-2A)卫星，首次实现集主被动传感器于一身，其中扫描微波辐射计是该星的4个微波载荷之一，采用圆锥扫描方式[3]，主要用于测量全球海洋表面温度、海面风速、海洋上空水汽和降雨等参数。

微波辐射计反演算法的研究为微波辐射计的应用提供了技术支持。使用微波辐射计的观测数据和可靠的反演算法能够获得海面温度、海面风速、大气中的水汽含量，云液态水含量等特定信息，这些信息对全球水循环以及气候变化等问题的研究提供了帮助。除此之外，对反演算法的深入研究还能够为仪器的设计(例如观测频率、观测天线位置等)提供合理的需求分析。在轨运行的微波辐射计系统中，AMSR系列由于其连续稳定的工作状态和相对广泛的应用基础，是目前研究最深入的星载微波辐射计。因此，基于AMSR-E开展的反演算法研究对于我国海洋动力环境卫星的发展具有一定的参考价值。

本文参考AMSR-E的仪器参数和说明文件(Algorithm Theoretical Basis Document，ATBD)，对比了几种线性反演算法和非线性反演算法。实验结果表明，星载微波辐射计的非线性反演算法虽然计算效率低于线性反演算法，但其物理意义明确且准确度更高，具有应用的价值。

2 反演算法概述

目前国际最常用的星载微波辐射计反演算法由“遥感系统”(Remote Sensing System，RSS)开发完成，Wentz参考Goodberlet，Swift和Wilkerson等人为SSM/I开发的GSW算法[4]，为AMSR开发了多元线性回归[5](Multiple Linear Regression，MLR)算法(该算法结构简单、计算快速)。RSS在2007年公布了与之类似的新的回归模型[6]，并增加了插值技术的使用，由于新模型中的二次项可以视为单独的一次项进行回归分析，因此这种新模型可以视为升级版多元线性回归模型。除了线性模型的反演方法，国内外的学者还研究了星载微波辐射计的非线性反演算法[7-8]。中国国家卫星海洋应用中心(National Satellite Ocean Application Services，NSOAS)的空间海洋遥感与应用研究重点实验室(Key Laboratory of Space Ocean Remote Sensing and Application，LORA)开发了基于Nelder-Mead的最优化反演算法[9]。

反演算法的理论基础是辐射传输模型(Radiative Transfer Model，RTM)。辐射传输模型建立了海面温度(Ts，单位K)，海面风速(W，单位m/s)，大气垂直积分水汽含量(V，单位mm，以下简称水汽含量)，大气垂直积分液水含量(L，单位mm，以下简称液水含量)等海洋大气参数与遥感卫星接收到的辐射亮温之间的关系，是反演计算的理论依据。基本关系可以表达为

TB=TBU+τ[ETs+TBΩ]

(1)

式中：TB为星载传感器接收到的总的辐射亮温，TBU为上行有效温度，τ为大气透过率，E为海面发射率，TBΩ为大气辐射的海面散射。此外，RTM还包括了观测频率、入射角等可以作为常数计算的仪器参数。辐射传输模型应用于不同微波辐射计的反演工作还需要考虑仪器参数的差别。两种典型的星载微波辐射计的主要参数如表1所示。

表1 在轨运行的微波辐射计相关参数的比较

3 线性模型反演海洋大气参数

3.1 多元线性回归反演海洋大气参数

多元线性回归算法可以表述为如下形式：

(2)

式中:Pj为反演所求的不同的海洋大气参数，R、I为线性方程。下标i为辐射计的通道(1=6.9V，2=6.9H，…)，下标j为反演的海洋大气参数(1=TS，2=W，3=V，4=L)，c为反演系数。反演系数可以采用模拟计算获得，也可以采用实际观测的微波辐射计亮温和现场观测的海洋大气参数配对所得的数据获得。

由于两个低频波段(6.9 GHz，10.7 GHz)与三个高频波段(18.7 GHz,23.8 GHz，36.5 GHz)对空气的吸收不同，因此回归方程采用如下形式：

I(TB)=TB,v=6.9,10.7 GHz

I(TB)=-ln(290-TB),

v=18.7,23.8,36.5 GHz

(3)

R(X)=X

(4)

在反演计算之前，需要对观测的辐射亮温进行关于入射角、海面风方向和海面盐度的修正。入射角和海面盐度可以简单地使用线性模型进行修正，而海面风方向在多元线性回归模型中只能采用180°的模糊修正。

3.2 升级版多元线性回归反演海洋大气参数

升级版多元线性回归算法的第一步是获得反演初步结果。反演系数的获取与多元线性回归算法类似：

(5)

ti=TBi-150,v=6.9,10.7,18.7,36.5 GHz

ti=-ln(290-TBi),v=23.8 GHz

(6)

第二步，RSS以海面温度和海面风速为例进行双线性插值：

(7)

理论上对于4个待求的反演结果，可以推广为希尔伯特空间的“四线性插值”，但这样的方法具有极大的计算规模，并不一定具有实际应用价值。式(7)的下标k表示3～34℃，下标l表示0～37m/s，以上插值范围按照实际需求做等分处理，一个方便的方法是将插值节点间隔取为1。据此，式(5)反演的初步结果将位于由等分间隔的海面温度和海面风速构造的插值格网。最终的反演结果可以写为这样的插值形式：

(8)

式中：权重系数w的计算与式(5)反演的初步结果距插值节点的距离相关。

考虑到海面盐度、入射角和海面风向的影响，最终反演的回归系数需要进行修正。盐度校正可以简单地使用线性模型进行修正，与多元线性回归模型相同。入射角和海面风向的校正采用双线性插值方法直接修正反演系数。入射角插值节点选为55°±1°，间隔0.5°；海面风向插值节点选为0°～180°，间隔20°。这种方法需要逐一计算每个反演时的温度和风速的插值节点处(38×38=1444个节点)的不同入射角和海面风向构成的另外一个维度上的插值节点(5×10=50个节点)，共需要计算72 200(1444×50)组反演系数。

这种升级的反演算法，其实质是使用局部的线性关系描述整体空间内的函数关系。式(7)和式(8)联立，可以看出对局部反演结果的插值同样等同于对反演系数进行插值。这与反演系数关于入射角和海面风向的校正的本质是一致的。值得一提的是，当这种方法在插值间隔上趋于无穷小(格网无穷密)，维度拓展到包含所有RTM的参量(一般情况，包括海面温度、海面风速、水汽含量、液水含量、海面盐度、入射角、海面风向等)的希尔伯特空间时，就与LORA开发的最优化方法反演海洋大气参数的算法核心相一致了。

4 非线性方法反演海洋大气参数

辐射计观测的辐射亮温可以表达为海面温度(Ts)、海面风速(W)、水汽含量(V)和液水含量(L)的函数：

TBi=fi(Ts,W,V,L)+ei

(9)

ei=eobsi+emi

(10)

式中：ei为观测亮温和RTM模拟亮温之间的误差，该误差的来源包括仪器产生的观测误差eobsi和模型误差emi。模型误差emi包括RTM与真实环境的误差ertmi和反演模型与RTM之间的误差erei。

4.1 牛顿法反演海洋大气参数

牛顿法是最常用的求解方程及方程组的方法。

牛顿方法中，式(9)被写为多元一阶泰勒展开的形式：

(11)

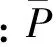
在不考虑观测亮温和RTM模拟亮温之间的误差(AMSR-E的ATBD所述，按照最小二乘法，这一项忽略与否并不关键)以及忽略高阶无穷小量时，式(11)可以写成如下形式：

AΔP+ΔT=0

(12)

式中：A为雅克比矩阵，有

(13)

(14)

已知x*是Ax=b的最小二乘解的充要条件为[10]，x*是ATAx=ATb的解。因此式(12)的最小二乘解为

ΔP=-(ATA)-1ATΔT

(15)

即

Pj=Pj(0)-(A(0)TA(0))-1A(0)TΔT(0)

(16)

因此有

Pj(k+1)=Pj(k)-(A(k)TA(k))-1A(k)TΔT(k)

(17)

式(17)就是牛顿法反演的迭代公式。迭代计算中，计算量最大的步骤在于雅克比矩阵的计算。这主要是由于fi的偏导数不方便获得解析式，只能使用数值微分来计算。这是十分不易进行的，因为无法准确地在一定的计算精度下找到合适的差商步长[11]：步长过大结果必然不准确；步长过小会导致切线和割线无法分别，造成计算错误。一个有用的方法是变步长差商。但由于计算量的原因，这显然不实用。除了这种情况，雅克比矩阵和(14)这两者都导致需要大量的计算fi。

4.2 最优化方法反演海洋大气参数

已知在式(9)中，TBi表示辐射计的第i个通道观测亮温，fi表示第i个通道的RTM。n个通道的亮温数据就可以构建一个n元非线性超定方程组。于是，得到一个关于观测亮温和均方误差(Mean Square Error，MSE)E的表达式：

TBi=fi(Ts,W,V,L)+ei

(18)

(19)

式中：ki是权重系数，表示各个观测通道的贡献程度。绝大多数情况，令ki为1或0是比较方便且合适的。

显然，当E取得最小值时，对应的(Ts，W，V，L)为这个非线性超定方程组的最优解。固定步长牛顿法是解决这类问题的一种常用的、基础的方法：

对于最优化问题minf(X)，k次迭代后得到Xk。将X=Xk在f(X)处二阶泰勒展开，有

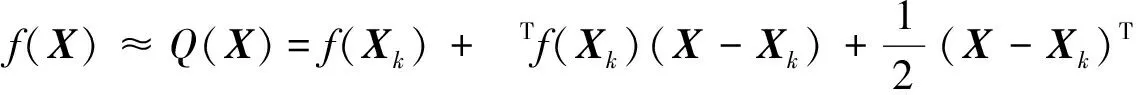
(20)

令

Q(X)=f(Xk)+2f(Xk)(X-Xk)=0

(21)

解(21)可得

Xk+1=Xk-[2f(Xk)]-1f(Xk)

(22)

然而，这种方法有显而易见的缺陷。首先，由RTM和观测亮温构成的方程组的黑塞矩阵的局部正定在数学上是不容易严格证明的，通常只能够从物理意义上说明它的正定性。其次，与式(13)类似，式(19)的二阶偏微分方便的计算方法仍然是使用数值微分技术，这种技术的缺点就是计算量大且依赖于差商计算中两点距离趋于无穷小的程度。

需要提出的是：式(19)中ki的设置是十分必要的。最优化方法与牛顿法，即传统的最小二乘法，最大的区别，就是最优化方法区分了观测误差的贡献程度。显然，最小二乘法可以认为是ki=1的最优化方法的解法。另一个实际的例子是，当某一通道的数据被认为是错误时，式(13)的雅克比矩阵显然会因此降低规模。与之对应，最优化方法中这一通道的k=0。因此，如果各个通道观测数据的测量误差分布不同以及对反演某一参数的贡献不同时，采用合理的方法推算ki的值将会是一件很有意义的工作。

基于以上分析，LORA的研究团队提出了使用Nelder-Mead(NM)算法的最优化方法反演大气海洋参数的方法，力求解决上述各种方法在反演时的缺陷。NM算法的最优化反演能够方便地求得式(19)中的最小值。NM算法[12-13]是一种直接搜索方法，借用了几何学中单纯形的概念。单纯形是一种N维空间中具有N+1个顶点的特殊多面体。常见的单纯形有1维空间中的直线，2维空间中三角形，3维空间中的四面体等。NM算法通过使用反射(reflection)，扩展(expansion)，收缩(contraction)和紧缩(shrink)四种运算技巧，不断调整N维空间的单纯形顶点使之逼近最优解。

5 仿真实验

基于AMSR的ATBD提供的参数化的RTM，建立了仿真数据库。通过这些仿真数据，使用参数化的RTM计算出模拟亮温。仿真数据库包含400 000组仿真数据，每组数据包含的物理量及分布范围如下：海面风向(0°～180°)，观测角(54.7°～55.3°)，海面盐度(32‰～37‰)，海面温度(0～30 ℃)，海面风速(0～20 m/s)，水汽含量(0～75 mm)，液水含量(0～0.3 mm)。数据分布采用平均分布的分布形式。

相对于多元线性回归反演每个参数使用全部10个通道的数据，基于NM算法的最优化方法反演不同的海洋大气参数时使用了不同的通道组合[14-15]。这样的处理方法在提高反演结果分辨率的同时，还能有效地减少计算量、提高计算效率。表2记录了反演不同参数的反演通道组合。

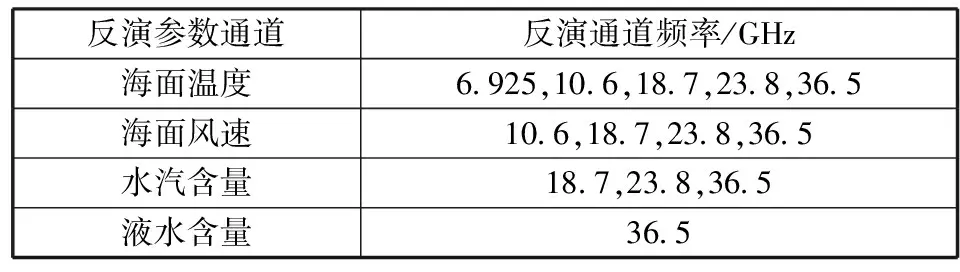
表2 非线性反演的通道选择

5.1 线性方法和非线性方法的反演结果比较

使用400 000组仿真数据、2000×243组真实数据和3种反演算法进行了实验，分析了多种反演算法的反演精确度及计算效率。表3是采用NM算法、多元线性回归算法、升级版多元线性回归算法分别对仿真数据进行反演实验的结果。可见，升级版的多元线性回归算法的反演精度优于多元线性回归算法，NM算法的反演精度优于升级版的多元线性回归算法。这几种反演算法的反演结果与目标数据之间的偏差(Bias)都很小，在1×10-4的数量级左右。NM方法反演的2010年5月1日升轨数据的海面温度结果如图1所示，反演结果的分布合理。和线性回归模型相比，非线性反演没有引入新的误差，因此,这种高精度的反演方法除了能提高反演产品的质量，还能够为在轨仪器定标提供准确的数据。

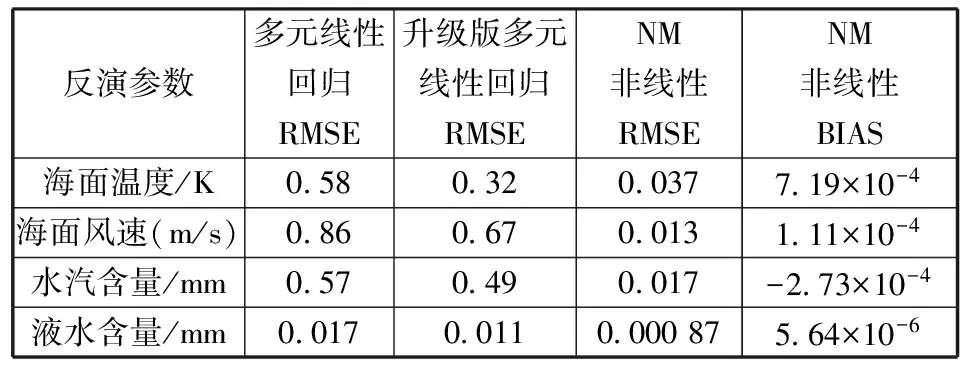
表3 3种反演算法的反演结果与仿真数据的比较

图1 NM算法反演AMSR-E升轨数据反演海面温度Fig.1 AMSR-E ascending SST by Nelder-Mead algorithm

5.2 线性方法和非线性方法的计算效率比较

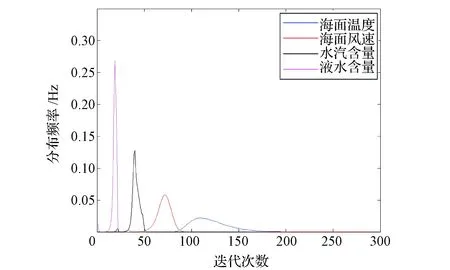
图2 NM的最优化算法反演的反演效率Fig.2 Retrieval time of the non-linear Nelder-Mead algorithm

多元线性回归由于采用简单的线性计算方式，在业务化应用中具有计算效率高的优点。与之相比，非线性迭代方法由于算法本身的复杂性，其计算效率远远低于多元线性回归。统计了使用基于NM算法的最优化反演400 000组数据时每一步的迭代次数以及反演AMSR-E的半轨2000×243组真实数据的反演耗时。对于4个不同的海洋大气参数，反演的迭代次数按照海面温度、海面风速、水汽含量和液水含量的顺序递减。使用单台HP-820Z图形工作站，基于NM的最优化方法反演2000×243组真实数据[16](见图2)的耗时约为90 min；多元线性回归反演这组数据的计算时间远小于非线性方法，约为0.5 min。因此，基于NM算法的最优化方法应用于业务化工作需要解决计算耗时的问题。

6 结束语

从线性算法和非线性算法两方面对反演方法进行了归纳讨论，具体包括：多元线性回归算法与升级版的多元线性回归算法；牛顿迭代算法与最优化算法。实验表明，LORA开发的基于NM的最优化反演算法与传统的星载微波辐射计的线性反演算法相比，物理意义明确、精度高1个数量级。在解决了计算耗时问题之后，该方法具有一定的研究价值和应用潜力。未来，随着星载微波辐射计系统的完善与发展，我们计划将计算快速的线性反演算法和具有明确物理意义的非线性反演算法相结合。预计新的联合反演方法能够为我国海洋系列卫星产品的综合应用提供更好的技术保障，同时为在轨定标等工作提供可靠的数据支持。

References)

[1]Kawanishi T, Sezai T, Ito Y, et al. The advanced microwave scanning radiometer for the earth observing system (AMSR-E), NASDA’s contribution to the EOS for global energy and water cycle studies[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41 (2)：184-194

[2]张升伟, 李靖, 姜景山, 等.风云3号卫星微波湿度计的系统设计与研制[J]. 遥感学报, 2008, 12 (2): 199-207

Zhang Shengwei, Li Jing, Jiang Jingshan,et al. Design and development of microwave humidity sounder for FY-3 meteorological satellite[J]. Journal of Remote Sensing, 2008, 12(2):199-207 (in Chinese)

[3]蒋兴伟,林明森,宋清涛. 海洋二号卫星主被动微波遥感探测技术研究[J]. 中国工程科学, 2013, 15 (7):4-11

Jiang Xingwei, Lin Mingsen, Song Qingtao. Active and passive microwave remote sensing technology of the HY-2A ocean satellite mission[J]. Engineering Sciences, 2013, 15 (7): 4-11 (in Chinese)

[4]Goodberlet M A,Swif C T,Wilkerson J. Ocean surface wind speed measurements of the Special Sensor Microwave/Imager (SSM/I)[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28 (5): 823-828

[5]Wentz F, Meissner T. Algorithm theoretical basis document:AMSR ocean algorithm,Version 2 [R]. Santa Rosa:Remote Sensing System,2000

[6]Wentz F J, Meissner T. Supplement 1 algorithm theoretical basis document for AMSR-E ocean algorithms[R]. Santa Rosa:Remote Sensing System, 2007

[7]王振占. 用19.35 GHz星载微波辐射计(SSM/I)亮温反演海面风速[J]. 海洋技术, 2003, 22(2): 1-6

Wang Zhennzhan. A model for inversing sea surface wind speeds by using SSM/I 19.35 GHz vertical and horizontal brightness temperatures[J]. Ocean Technology, 2003, 22(2): 1-6 (in Chinese)

[8]王振占. 海面风场全极化微波辐射测量[D]. 北京. 中国科学院空间科学与应用研究中心, 2005

Wang Zhenzhan,Sea surface wind vector measured by polarimetric microwave radiometer[D]. Beijing:National Space Science Center,CAS, 2005 (in Chinese)

[9]王兆徽, 宋清涛, 蒋兴伟, 等. 星载微波辐射计的非线性反演算法[J]. 高技术通讯, 2015(5)

Wang Zhaohui, Song Qingtao, Jiang Xingwei, et al. Non-linear retrieval algorithm for passive satellite microwave radiometer[J]. Chinese High Technology Letters, 2015(5) (in Chinese)

[10]Lawson C L, Hanson R J. Solving least squares problems[M]. Philadelphia: SIAM: 1974

[11]Mathews J H, Fink K D. Numerical methods using MATLAB[M]. Upper Saddle River: Prentice Hall, 1999

[12]Nelder J A, Mead R. A simplex method for function minimization[J]. Computer Journal, 1965, 7(4): 308-313

[13]Powell M J. On search directions for minimization algorithms[J]. Mathematical Programming, 1973, 4(1): 193-201

[14]Gentemann C L, Meissner T,Wentz F J. Accuracy of satellite sea surface temperatures at 7 and 11 GHz[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1009-1018

[15]Martin S, An introduction to ocean remote sensing[M]. Cambridge: Cambridge University Press: 2004

[16]National Snow & Ice Data Center. NSIDC. AMSR-E L2A data[ED/OL]. [2014-11-01]. Ftp://n5eil01u.ecs.nsidc.org/AMSA/AE_L2A.003

(编辑：张小琳)

Comparison of Linear and Nonlinear Retrieval Algorithm for Spaceborne Microwave Radiometer

WANG Zhaohui1LIU Yuxin1,2SONG Qingtao1,2WU Binfeng1

(1 National Satellite Ocean Application Service, Beijing 100081, China) (2 Key Laboratory of Space Ocean Remote Sensing and Application, SOA, Beijing 100081, China)

The paper analyzes the channel choice of ocean retrieval algorithm and compares the differences between linear and nonlinear retrieval algorithm by spaceborne microwave radiometer data process. To discard the low-frequency channel in nonlinear retrieval algorithm gradually is a direct and effective way to improve the spatial resolution of retrieval products. Several analyses and experiments for retrieval algorithm indicate that compared with the linear retrieval algorithm, the optimization algorithms based on Nelder-Mead method has higher accuracy, application and development potential.

spaceborne microwave radiometer; retrieval algorithm; Nelder-Mead algorithm

2015-06-09；

2015-07-15

国家自然科学基金(41276019)；海洋公益性行业科研专项(201305032)；中法海洋卫星预先研究项目

王兆徽，男，硕士，研究方向为微波海洋遥感。Email:wzh@mail.nsoas.org.cn。

V443

A

10.3969/j.issn.1673-8748.2015.04.021