IMU的加速度计误差参数辨识方法研究
王 力,习先强
(中国民航大学电子信息与自动化学院,天津 300300)
作为惯性导航系统的高端用户,民用航空也是惯性测量单元(IMU,inertial measurement unit)的重要服务对象。IMU 固连在飞机上,直接测量飞机的加速度与角速度,通过航位推算,实时得到飞机与地球之间的相对速度、经度、纬度及高程等飞机航行所需要的信息。民航对安全性要求很高,不同飞行阶段、不同飞行操作对IMU 的精度完好性和稳定性的要求不同。因此,提高民航飞机惯性导航系统的精度非常重要。加速度计作为IMU 中测量运载体加速度的惯性器件,凭借其体积小、重量轻、价格低、寿命长和易批量生产等优点,广泛应用于航空航天、陆地及海上等军事领域,是现代国防系统的核心技术产品[1]。随着军民融合发展战略的实施,加速度计已扩展到各个领域,如民用领域中的移动机器人、自动驾驶等及工程领域中的石油管道测量、海上浮标状态监测、结构组件变形测量等,加速度计在这些系统中发挥着至关重要的作用[2-4]。
加速度计精度的高低直接影响到其应用范围,作为IMU 的核心器件之一,加速度计的性能和输出数据的有效性、准确性直接影响到IMU 的测量精度。提高加速度计精度的主要措施有两种:一是改进加速度计的结构工艺和加工工艺,探索新型加速度计;二是对加速度计和系统进行测试和建模,通过误差补偿来提高器件的实际使用精度和系统精度[5-7],这种方法在实际工程应用中最有意义。
IMU 中的3 个加速度计正交安装,分别测量三维坐标轴下的加速度信息,但由于结构的不正交误差及人为的安装误差等因素,加速度计的输出量包含多种误差,与实际值不相符,因此需要研究加速度计的输入输出关系,建立加速度计的输出误差模型,对误差参数进行辨识。传统的加速度计误差参数辨识方法有重力场静态翻滚法、六位置法等[8-10]。针对实验室的要求,在传统六位置法的基础上,运用了24 位置法对加速度计进行误差参数辨识。基于此设计了24 位置法的标定过程,并建立了加速度计组件的误差参数模型,通过三轴转台进行位置试验辨识出误差参数。结果表明,此方法能够辨识出误差参数,建立的误差参数模型准确。
1 加速度计组件误差模型建立
1.1 输入输出模型
根据加速度计自身的精度或使用场合,可得到简化的输入输出数学模型为

其中:Aint为输出加速度值(g);E 为加速度计的输出(脉冲);K1为标度因数;K0为偏值;ai为沿输入基准轴的加速度分量。
1.2 不对准角
实际工程应用中,加速度计组件轴系与载体系存在安装误差,使加速度计的安装坐标系与载体系非正交。加速度计组件系与载体系由3 组6 个不对准角μxz,μxy,μyz,μyx,μzy,μzx描述,如图1所示。
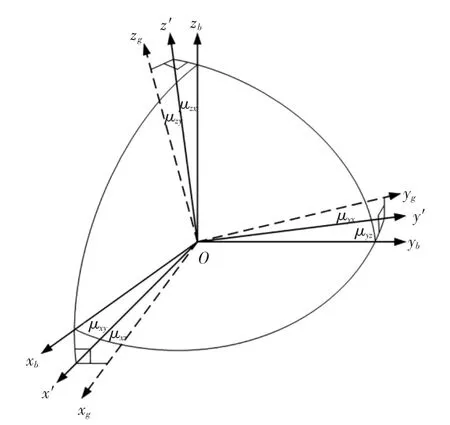
图1 加速度计不对准角Fig.1 Accelerometer misalignment angle
其中:Oxgygzg为加速度计测量组件系;Oxbybzb为载体系,Ox′为Oxg在Ozbxb上的投影,Ox′与Oxg的夹角为μxz,Ox′与Oxb的夹角为μxy;Oy′为Oyg在Oxbyb上的投影,Oy′与Oyg的夹角为μyx,Oy′与Oyb的夹角为μyz;Oz′为Ozg在Oybzb上的投影,Oz′与Ozg的夹角为μzy,Oz′与Ozb的夹角为μzx。
1.3 输出误差模型
由加速度计的输入输出数学模型可知,IMU 中3个加速度计的输出中包含零偏误差和安装误差。加速度计的零偏误差指输入比力为0 时加速度计的输出值,因此,根据式(1)可建立加速度计组件的误差模型为
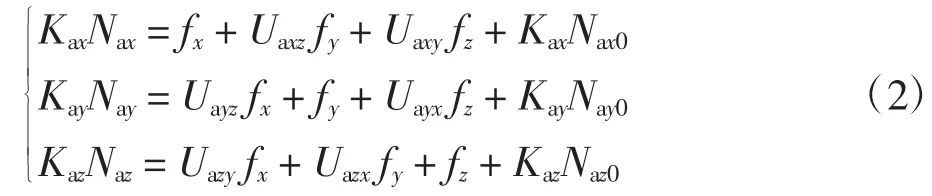
其中:Kax、Kay、Kaz分别为加速度计测量组件3 个轴上加速度计的标度因数(m·s-1/脉冲);Nax、Nay、Naz分别为加速度计测量组件3 个轴上加速度计的数字输出(脉冲/s);fx、fy、fz分别为载体系3 个轴的输入比力(m/s2);Uaxz、Uaxy、Uayz、Uayx、Uazy、Uazx分别为加速度计测量组件与载体系间的不对准角(′);Nax0、Nay0、Naz0分别为3 个轴上加速度计的零位偏置(脉冲/s)。
2 24 位置法的误差参数辨识
要辨识出模型参数,即要辨识出加速度计的标度因数、不对准角和零位偏置。实验室条件下,一般利用三轴转台进行位置试验标定出加速度计的误差参数(位置试验采用的三轴转台是经过严格标校过的,可以认为其误差非常小,可忽略不计)。试验过程中IMU固联在转台上,将转台视为载体,即转台系与载体系重合,载体系基于“东北天”坐标系。标定即为将加速度计的测量值补偿投影到以转台3 个轴系确定的正交坐标系上,如图2所示。
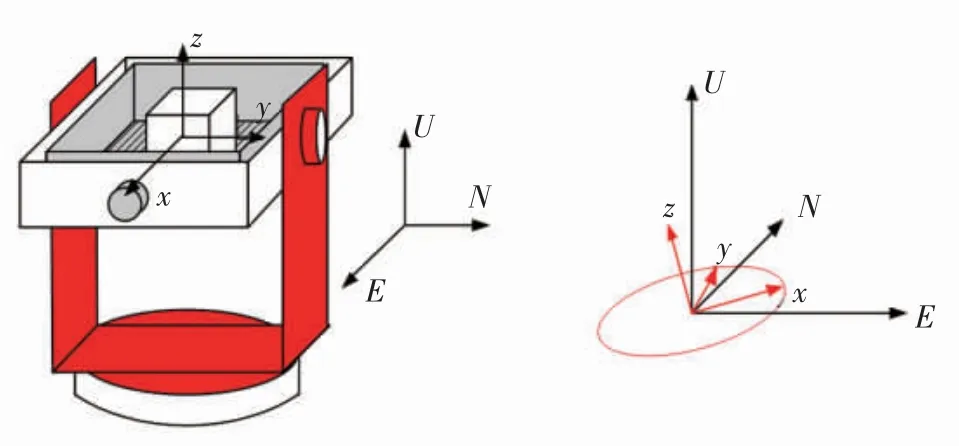
图2 加速度计的安装方式Fig.2 Accelerometer installation
图2中,载体系的正方向分别为:东向E、北向N、天向U。对于IMU 中的加速度计组件,安装方式为:X加速度计指向东向,Y 加速度计指向北向,Z 加速度计指向天向即垂向。
2.1 原理
依据加速度计坐标轴的指向不同,常规的六位置法可分为3 组,每组进行2 次测试,在静基座条件下,可标定出误差参数。然而常规的六位置算法对设备要求高,可能会存在测量误差过大而导致标定不准确的结果。所以在此基础上,设计了24 位置标定算法,对加速度计的输出误差模型系数进行辨识。24 位置法的原理如表1所示。

表1 24 位置法原理Tab.1 Principle of 24-position method
表1中:“Z 朝天”表示Z 加速度计此时的的测量方向是“东北天坐标系下”向上,输出为正方向,理论上能测量到的加速度值为g;“Z 朝地”表示Z 加速度计此时的测量方向是“东北天坐标系下”向下,输出为反方向,理论上能测量到的加速度值为-g;。24 位置法中,分别能标定出IMU 中的3 个加速度计的误差参数,当Z 加速度计朝天时,三轴转台的外框位置分别在0°、90°、180°、270°位置处静止一段时间,当Z 加速度计朝地时,三轴转台的外框位置同样静止在这4 个位置一段时间。由Z 加速度计正反试验的输出值能标定得到Z 加速度计的某些误差参数,同理对X 和Y 加速度计也可以标定得到相关的误差参数。
2.2 误差参数
加速度计的零位偏置可表示如下

其中:Naxij(t)、Nayij(t)、Nazij(t)为加速度计X、Y、Z 在上述24 位置的数字信号输出。
由X 加速度计的误差参数公式可得到
其中:Naxi为X 加速度计在上述第i 个位置的数字信号输出均值,Kax、Uaxz、Uaxy、Nax0为待求的X 加速度计的标度因数、不对准角和零位偏置。
将X 加速度计的辨识模型表示为

其中
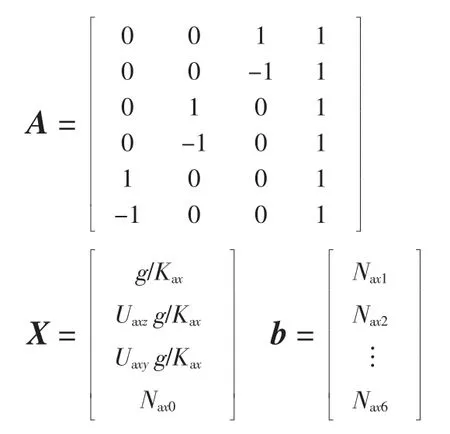
其中,A 为列满秩的,方程的最小二乘解为

根据位置试验数据即可辨识X 加速度计的误差参数,同理可得Y、Z 加速度计的误差参数。
3 实验设计和结果
3.1 实验方案
按24 位置法调整三轴转台24 次,在每个给定位置上静止一段时间,使加速度计敏感当地垂线重力加速度,记录加速度计的输出1 s 脉冲和数据。标定的方案如表2所示,静止时长为3 min,位置试验时长约为75 min。转台每转动一个位置后,载体系的x、y、z 轴指向也随之变化,可看出初始位置x、y、z 方向为东北天。
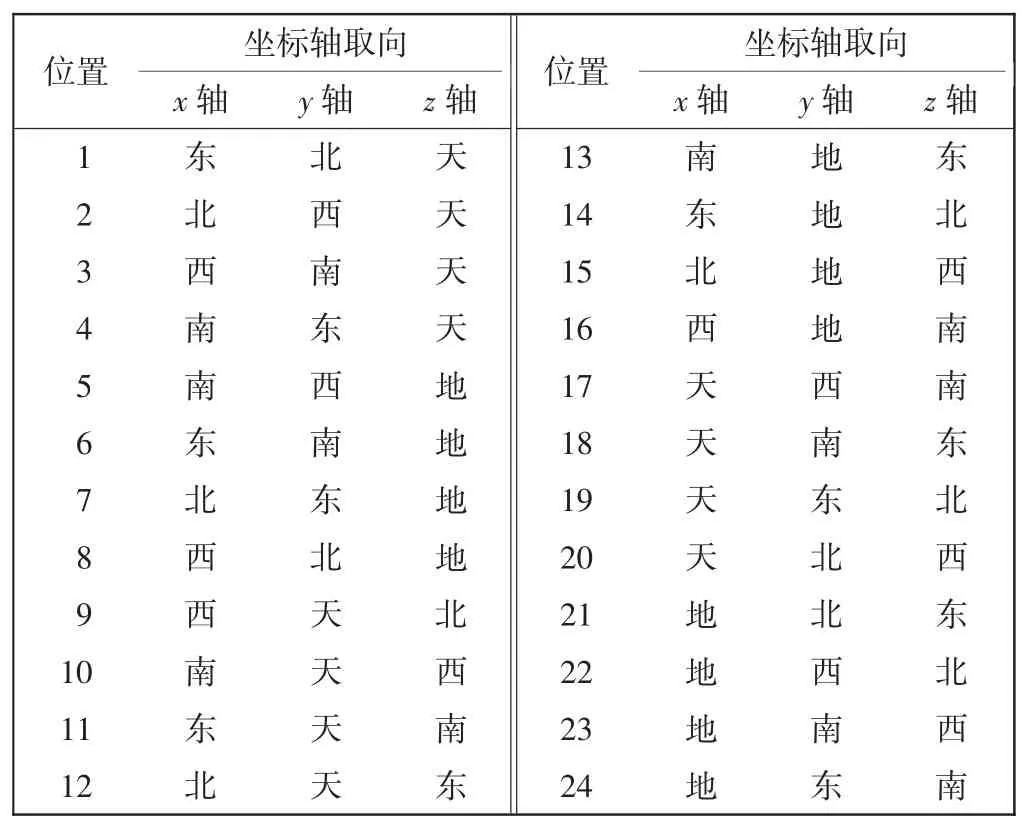
表2 24 位置法标定方案Tab.2 Calibration scheme of 24-position method
3.2 实验步骤
加速度计24 位置法的标定过程如下:
1)将装有3 个加速度计的IMU 安装于转台台面的中心,z 轴垂直于转台台面,x 轴和y 轴平行于转台台面;
2)接通IMU 的电源,预热一段时间,待加速度计输出稳定后设置转台按照表2的方案进行实验,转台设定24 个位置;
3)在每个位置静止3 min,采集3 个加速度计的输出信号,求得每个位置的平均值作为3 个加速度计在该位置的输出值;
4)计算3 个加速度计的误差参数。
3.3 实验结果分析
试验结束后,采集3 个加速度计试验过程中的数据,按照前文给定的公式对加速度计的标度因数、不对准角和零位偏置进行计算分析,得到的结果如表3所示。
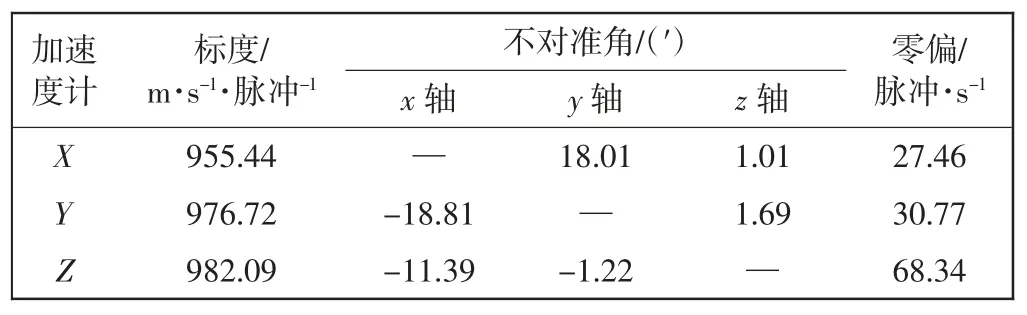
表3 加速度计误差参数辨识结果Tab.3 Error parameter identification result of accelerometer
由表3可得,3 个加速度计的输出信号为脉冲数,经过计算得到的加速度计标度因数、不对准角、零偏各不相同。由辨识得到的误差参数可求出3 个加速度计的输出误差模型分别如下
1)X 加速度计
955.44 Nax=fx+18.01fy+1.01fz+26 243.18
2)Y 加速度计
976.72 Nay=-18.81fx+fy+1.69fz+30 053.67
3)Z 加速度计
982.09 Naz=-11.39fx-1.22fy+fz+67 117.16
加速度计组件的实际输出值为地球重力加速度的分量,根据加速度计组件输出误差方程,在每个位置处计算合加速度值,与当地的重力加速度进行对比,如图3所示。
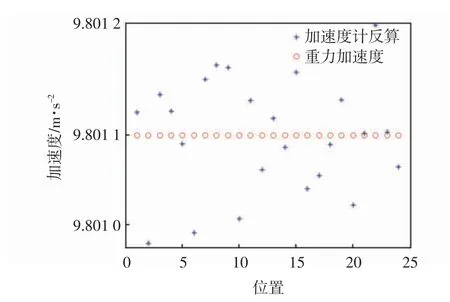
图3 加速度计误差模型估计Fig.3 Estimation given by accelerometer error model
图3中明显可看出,利用加速度计误差方程反算得到的加速度值接近于重力加速度,第22 个位置处的误差最大,且最大的误差为10-6g,该加速度计的精度为2×10-6g,误差在精度范围内。因此可得出,24 位置法辨识得到的加速度计误差参数精度较高,建立的误差方程准确。
4 结语
24 位置法能够辨识出加速度计的标度因数、不对准角、零位偏置等相关误差参数。这种方法原理简单、易于实现、准确有效,实验结果表明其能满足民航飞机导航系统的要求。建立的加速度计误差方程能准确反映加速度计的输出情况,为惯导系统的误差补偿提供依据,对提高民航飞机惯性导航系统的精度具有重要的意义。

