无人机级联中继通信航迹规划方法

刘海涛，方晓钰，顾新宇，李冬霞

（中国民航大学天津市智能信号与图像处理重点实验室，天津 300300）

与固定中继通信相比，无人机（UAV，unmanned aerial vehicle）中继通信凭借其通信覆盖范围大、位置灵活可控、通信系统构建快与维护成本低等优势，已在军用与民用领域得到了广泛的应用[1-2]。然而，由于中继UAV 的高速移动、续航能力受限、飞行姿态变化，UAV 中继通信系统产生了一系列新问题，如航迹规划环境多变复杂，系统通信性能如何提高等，因此针对UAV 中继通信系统存在的问题，展开技术上的关键研究具有重大意义。

目前，国内外围绕UAV 中继通信系统中航迹规划的相关研究如下：针对点对点中继通信的UAV 航迹优化问题，文献[1]提出一种基于空时分组编码的UAV 中继通信传输方法；为提高UAV 级联中继通信系统传输的可靠性和有效性，文献[2]在高斯白噪声信道环境下基于人工势场法提出UAV 航迹规划方法，研究表明基于人工势场法的优化方案能明显改善UAV 中继通信系统的通信质量，但在系统建模过程中没有考虑信道小尺度衰落对UAV 航迹规划的影响；文献[3]基于系统信道容量最大化准则给出中继通信的UAV 飞行控制方法，结果表明所提方案可有效提高传输信道容量，但没有考虑移动地面节点对UAV航迹的影响。

针对地面节点运动和信道衰落情况下的点对点UAV 级联中继通信系统中的航迹规划问题，基于遍历容量最大化准则提出了两种UAV 航迹规划方法：级联UAV 航迹联合优化方法与分步优化方法，并利用FM-EM（finite mixture-expectation maximum）算法推导给出了UAV 级联中继通信系统的中断概率计算表达式，最后利用计算机仿真对所提航迹优化方法进行验证。仿真结果表明所提优化方案能显著改善UAV 级联中继通信系统的可靠性。

1 UAV 级联中继通信系统

1.1 系统模型

UAV 级联中继通信系统模型如图1所示。系统由移动用户节点（MU，mobile user）、两架固定翼无人机（分别记为UAV-1 和UAV-2）及固定基站（BS，base station）4 部分组成。

图1 无人机级联中继通信系统模型Fig.1 UAV cascaded relay communication system model

假设MU 与BS 之间通信距离较远，不存在直达通信链路，因此必须通过两架UAV 级联中继通信才可实现MU 与BS 的通信。此外，为了简化系统，假设MU、UAV 及BS 节点均配置单根天线，UAV 采用放大转发方式进行中继通信。假设两架UAV 的距离较远，不考虑碰撞问题。

1.2 信号模型

由于UAV 采用放大转发方式实现中继通信，MU—BS 的通信需要3 个时隙。t 时刻，第1 个时隙MU 发送信号至UAV-1，则UAV-1 接收信号[4]表示为

其中：PM为MU 的发射功率；为MU 与UAV-1 之间的信道衰落系数；s 为MU 的发射信号，且满足E（|s|2）=1；为t 时刻UAV-1 接收天线在第1 个时隙接收到的复高斯白噪声，服从均值为0，方差为σ2M的复高斯分布（0，σ2M）。在第2 个时隙，UAV-1 接收来自MU的信号，将其乘以一个增益因子并以一定的功率将接收信号转发至UAV-2，则第2 个时隙UAV-2 接收信号表示为

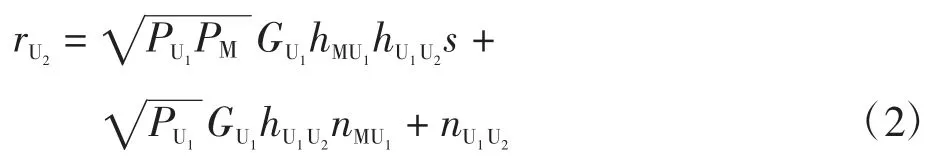
UAV-2 接收到UAV-1 发送信号后，同样将接收到的信号乘以一个增益因子，即

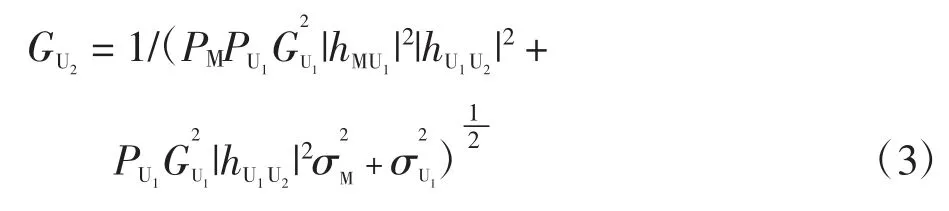
然后，UAV-2 以一定的功率将信号转发至BS。在第3个时隙，BS 接收信号表示为

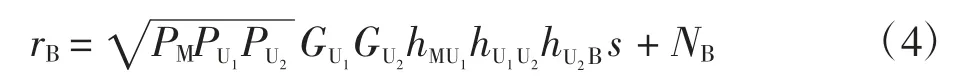
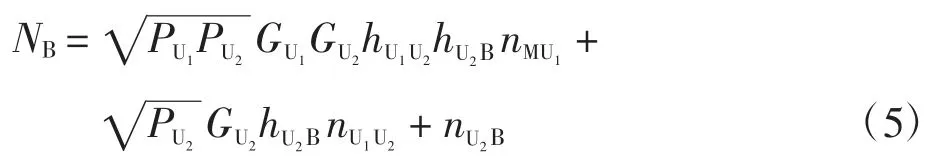
1.3 UAV-2 与BS 接收机输出信号的瞬时SNR

假设MU—UAV-1，UAV-1—UAV-2，UAV-2—BS 的信道衰落系数hX为包含路径损耗的瑞利信道，具体建模为

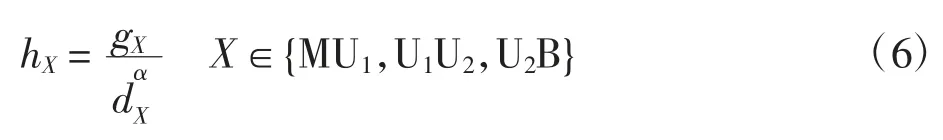
其中，gX为小尺度衰落系数，服从（0，1）；α 为信道的路径损耗因子；dX为各节点之间的距离。根据式（2）、式（4）和式（6），可计算得到UAV-2 与BS 接收机输出信号的瞬时信噪比（SNR）分别为

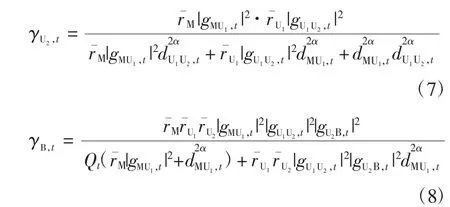
2 级联UAV 最佳航迹规划方法

在UAV 级联中继通信系统中，MU 与UAV-i（i=1，2）的位置在不断变化，为了获得最佳的通信系统性能，需根据MU 的运动实时优化UAV-1 与UAV-2 的航迹。考虑到无线通信系统的遍历容量是衡量系统性能的一项重要技术指标，因此，基于遍历容量最大化准则给出级联UAV 航迹联合优化方法与分步优化方法。

2.1 联合优化方法

在t 时刻UAV 级联中继通信系统的遍历容量表示为

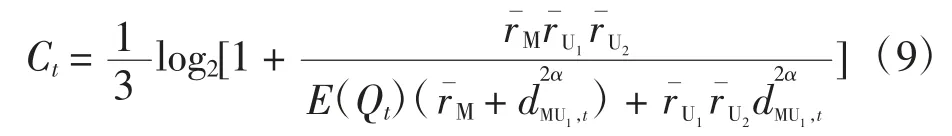
为计算各节点间的距离，首先建立三维直角坐标系，假设t 时刻MU、UAV-i（i=1，2）及BS 的位置向量分别为=[xByB0]T，使用其可计算得到和

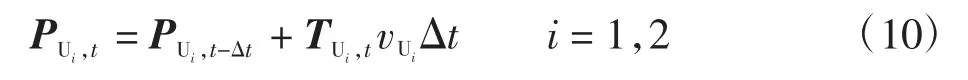
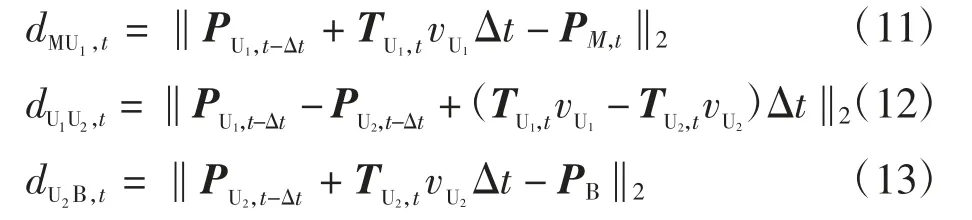
其中：‖·‖2表示2-范数。由式（11）～式（13）可知，t 时刻系统的遍历容量仅取决于UAV-i 的航向角。

为了使t 时刻UAV 级联中继通信系统性能最优，基于遍历容量最大化准则优化UAV-i 的航向角。假设UAV-i 的最大转弯角δmax相同，则上述优化问题表示为

考虑到log2（·）为单调递增函数，且影响BS 节点信噪比大小的因素都集中在式（9）的分母，因此，式（14）中的优化问题进一步表示为

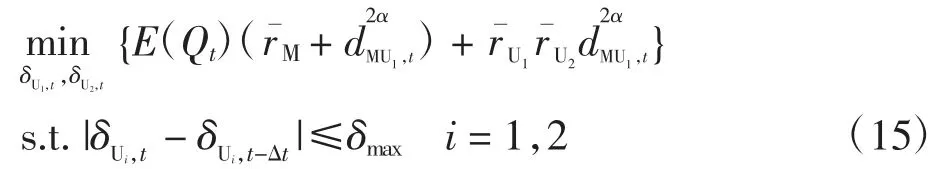
式（15）中的优化问题是二维边界约束的非线性优化问题，可转化为无约束优化问题求解。首先令

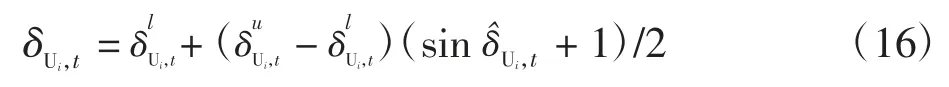
将式（16）代入式（15），则优化问题转化为

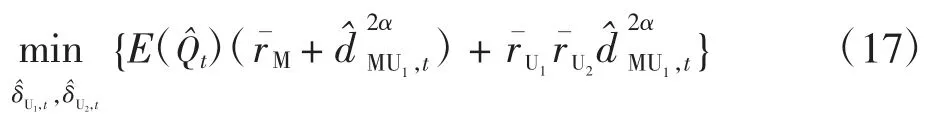
该问题可通过Nelder-Mead 单纯形算法[6]解决。最后将求解得到的代入式（16）可计算得到UAV-i 在t 时刻的最佳飞行航向角。

2.2 分步优化方法

2.2.1 UAV-1 航迹规划方法

在该系统中，当MU 节点处于运动时，为保证系统链路性能最优化，UAV-1 节点需要快速跟踪MU 节点的位置变化，而UAV-2 节点则跟踪UAV-1 节点的变化。相对于UAV-1 位置的变化，UAV-2 位置改变较缓慢，进一步考虑到单个位置更新周期内，UAV-2 节点位置改变不大，因此，在优化t 时刻级联UAV 航向角时，可首先假设UAV-2 节点位置无变化，此时针对MU—UAV-1—UAV-2 链路优化UAV-1 的航向角，随后以优化得到的t 时刻UAV-1 的最佳航向角为基础，针对MU—UAV-1—UAV-2—BS 链路优化t 时刻UAV-2 的航向角。以上处理方法将级联UAV 的联合航向角优化转换为级联UAV 的分步航向角优化。

根据式（7），t 时刻MU—UAV-1—UAV-2 通信链路的遍历容量近似表示为

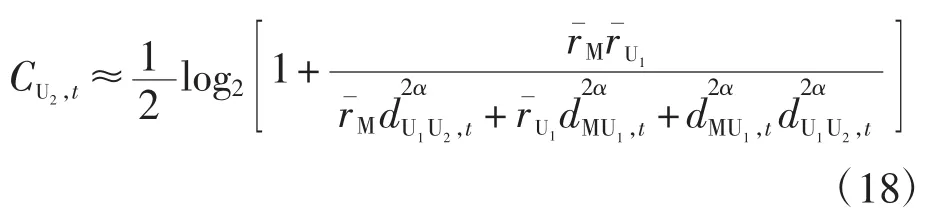
假设UAV-1 在t-△t 时刻通过卡尔曼滤波估计得到t 时刻MU 的位置为，则可重新表示为

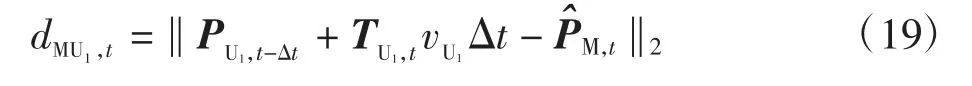
考虑到在一个位置更新周期内，UAV-2 移动距离相对较小，因此，由t 时刻UAV-1 的位置向量与t-△t 时刻UAV-2 的位置向量确定，即表示为

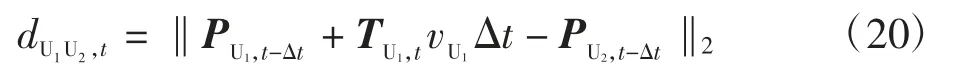
根据式（19）和式（20），可得到以下结论：在t-△t时刻UAV-1 的位置给定后，t 时刻MU—UAV-1的距离及UAV-1—UAV-2 的距离仅决定于t 时刻UAV-1 的航向角，则t 时刻MU—UAV-1—UAV-2 通信链路遍历容量仅取决于t 时刻UAV-1 的航向角。因此，为使t 时刻该链路遍历容量最大，基于MU—UAV-1—UAV-2 链路遍历容量最大化准则来优化UAV-1 的航向角，以上优化准则表述为

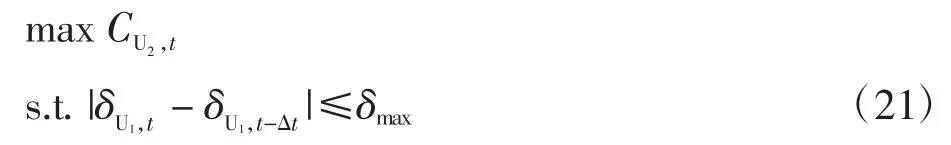
考虑到log2（·）为单调递增函数，式（21）的优化问题转化为

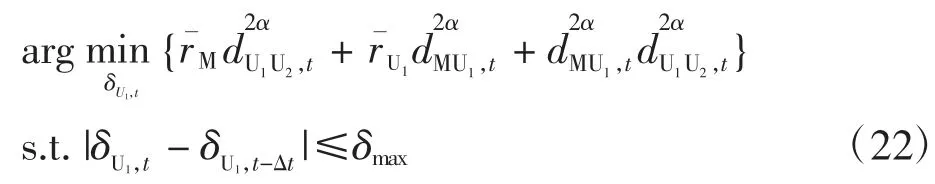
式（22）优化问题为一维线性约束的非线性优化问题，该优化问题可通过一维线性搜索方法解决。

2.2.2 UAV-2 航迹规划方法

当UAV-1 在t 时刻的最佳航向角被确定后，系统的遍历容量仅受UAV-2 航向角的影响。为了使系统遍历容量最大，基于MU—UAV-1—UAV-2—BS 链路遍历容量最大化准则来优化UAV-2 的航向角。因此，式（15）的优化问题可等效为

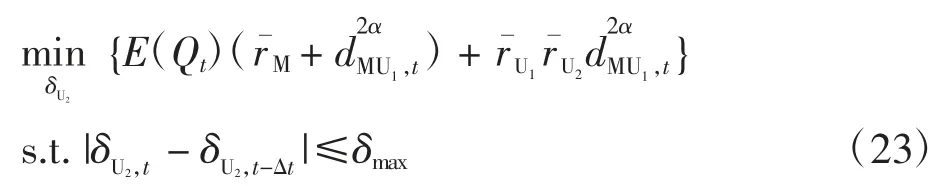
由式（24）可看出，在t-△t 时刻UAV-2 的位置确定的情况下，仅决定于UAV-2 的航向角，因此式（23）的优化问题进一步转化为

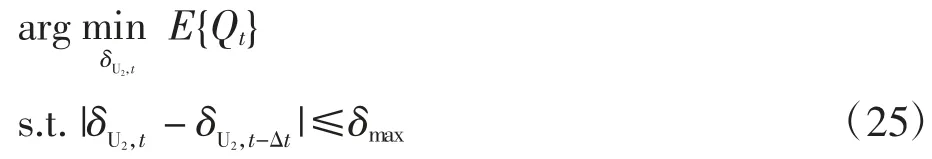
式（25）的优化问题可通过一维线性搜索法解决。

3 系统中断概率

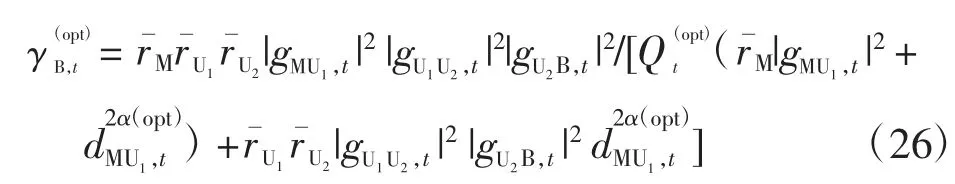
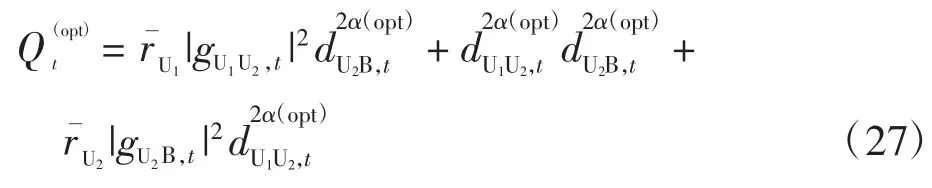
中断概率是衡量无线通信系统链路传输质量的一项重要质量指标，定义为通信系统的输出信噪比低于某一门限值γth的概率，即

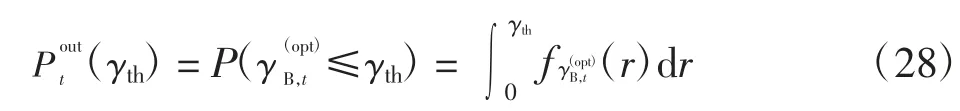
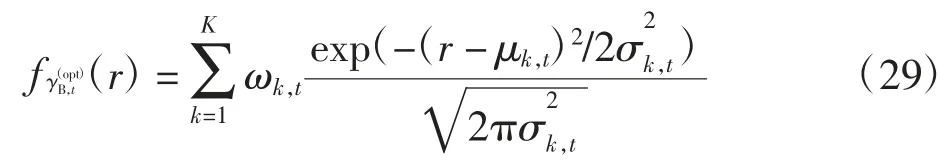
其中：K 为FM 模型中混合项的个数；参数μk，t，分别为t 时刻第k 个混合项的均值与方差；ωk，t＞0 为t时刻第k 个混合项的加权系数，且满足利用EM 算法估计式（28）中的未知参数可参考文献[7]。将式（29）代入式（28），可计算得到

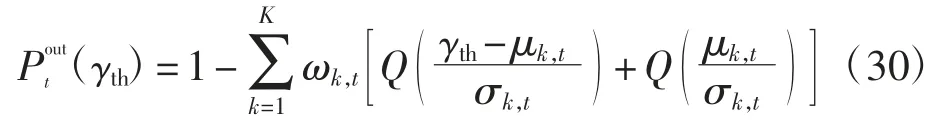
其中：Q（x）为高斯函数（Q 函数是标准正态分布的右尾函数），满足

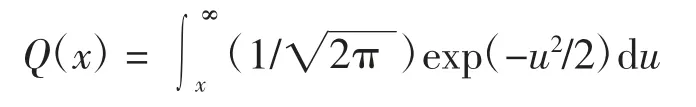
4 数值仿真

4.1 参数设置

通过计算机仿真验证所提出级联UAV 航迹规划方法的有效性与正确性。系统由MU，UAV-1，UAV-2和BS 节点组成，其具体参数设置如下：MU、UAV-1、UAV-2 与BS 的初始位置坐标分别为（500，1 000，0），（500，250，350），（4 500，4 750，350），（4 500，4 000，0）；路径损耗因子α = 1；UAV-i（i=1，2）与MU 的位置更新周期△t=1 s，系统仿真时间为T=300 s；=Pi/σ2i（i = M，U1，U2）设置为75 dB；中断门限γth= 4 dB；利用一阶自回归模型仿真MU 的运动轨迹，MU 的移动速度vM=20 m/s；另外假设MU 在t = 110 s 时改变方向，转向时的速度满足=-1.885 6；UAV-i（i=1，2）的飞行高度设置为350 m，飞行速度为40 m/s。

4.2 结果与分析

最大转弯角δmax为10°时，UAV 采用联合优化方法与分步优化方法得到的最佳航迹，如图2所示。可看出：①采用联合优化方法与采用分步优化方法得到的UAV-i（i=1，2）的最佳航迹几乎重合；②靠近MU的UAV-1 的飞行范围较UAV-2 的飞行范围大，是由于UAV-1 跟随MU 的路径变化飞行，而UAV-2 跟随UAV-1 的航迹变化飞行。

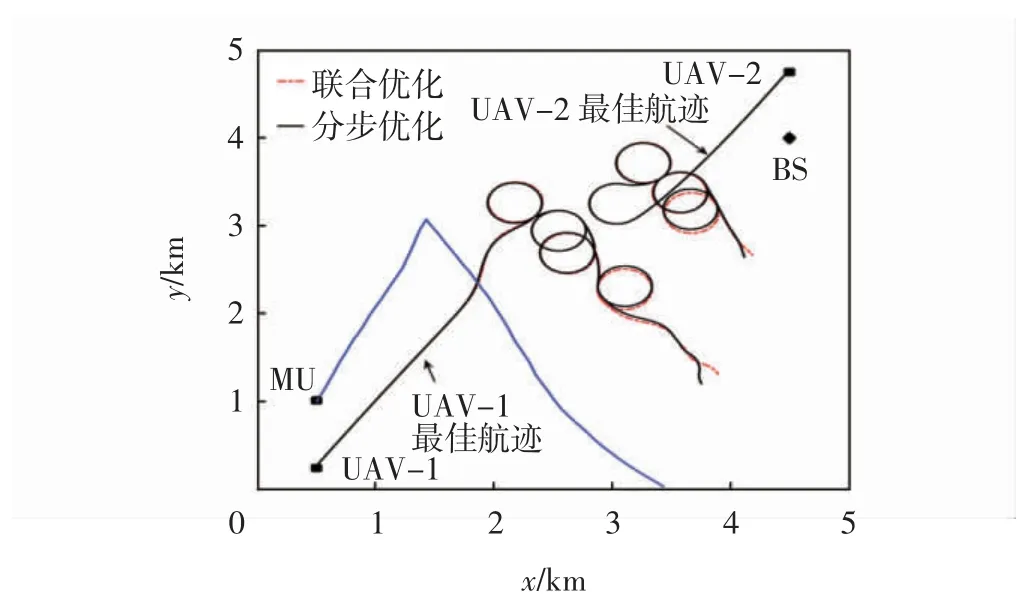
图2 UAV-i（i=1，2）最佳航迹随MU 运动变化的曲线Fig.2 Optimal trajectories of UAV-i（i=1，2）changing with MU mobility

最大转弯角σmax为10°时，系统中断概率随时间变化的曲线，如图3所示。可看出：采用分步优化与联合优化得到的系统中断概率曲线基本重合，表明所提的分步优化方法合理有效。

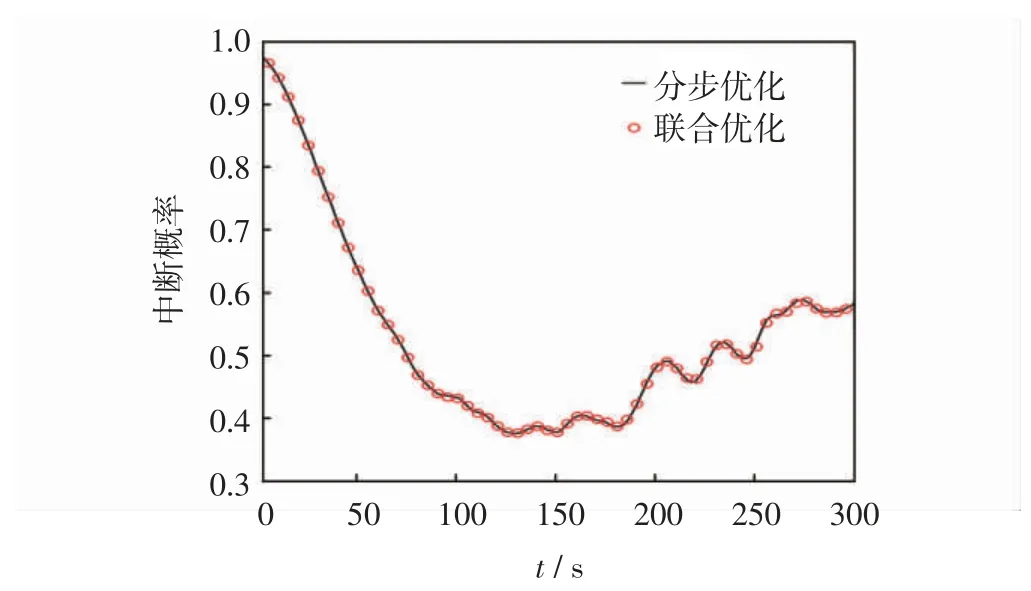
图3 系统中断概率随时间变化曲线Fig.3 Outage probability vs.time

最大转弯角σmax为5°和15°时，UAV 采用分步优化方法得到的最佳航迹随MU 运动变化的曲线，如图4所示。可看出UAV 绕圆飞行的半径随着最大转弯角的增大逐渐减小，由于随着最大转弯角的增大，角加速度也随之增大，因此通过减小飞行半径以维持切向加速度的大小。

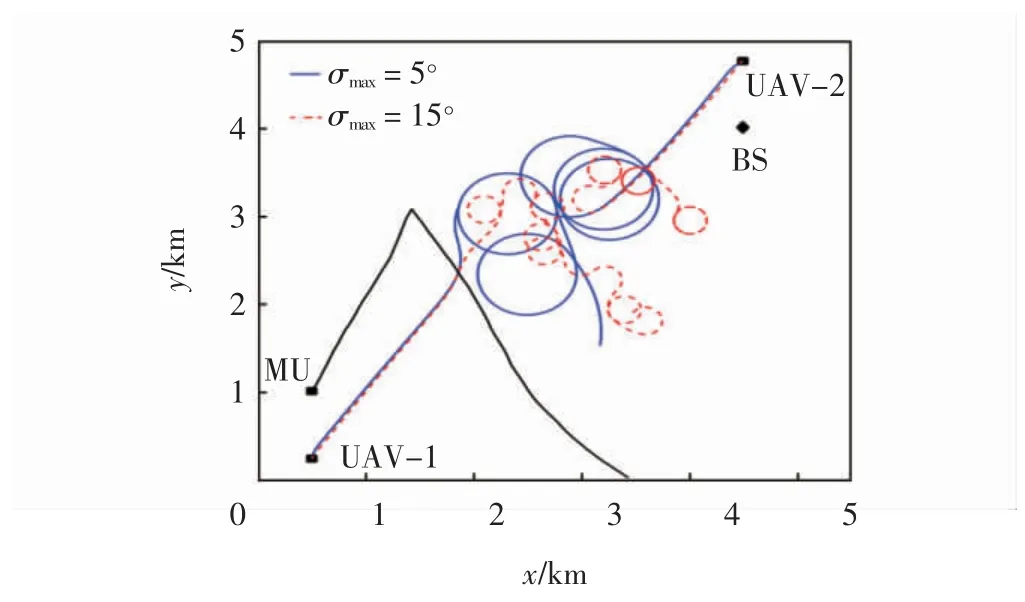
图4 最大转弯角对UAV-i（i=1，2）最优航迹的影响Fig.4 Impact of maximum turning angle on optimal trajectories of UAV-i（i=1，2）

最大转弯角σmax为5°和15°时，中继通信系统中断概率随时间变化曲线，如图5所示。可看出增大UAV的最大转弯角能提高UAV 级联中继通信系统性能。

图5 最大转弯角对系统中断概率的影响Fig.5 Impact of maximum turning angle on outage probability

图6对比两种设计方案下的UAV 最佳飞行轨迹，可看出：所提优化方案下的UAV 通过协同合作将信息传输至基站节点，从而提高系统链路传输的可靠性。

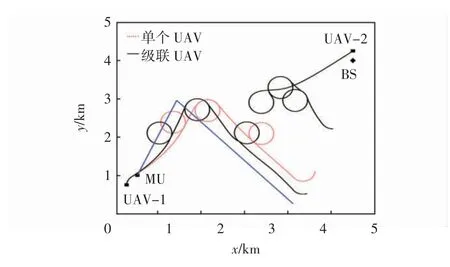
图6 不同方案下的UAV 最优航迹Fig.6 Optimal trajectories of UAV with different plans

两种设计方案下的中断概率曲线如图7所示。可看出：级联UAV 中继通信系统的中断概率均低于单个UAV 中继通信系统的中断概率，说明级联可明显改善通信系统的可靠性。

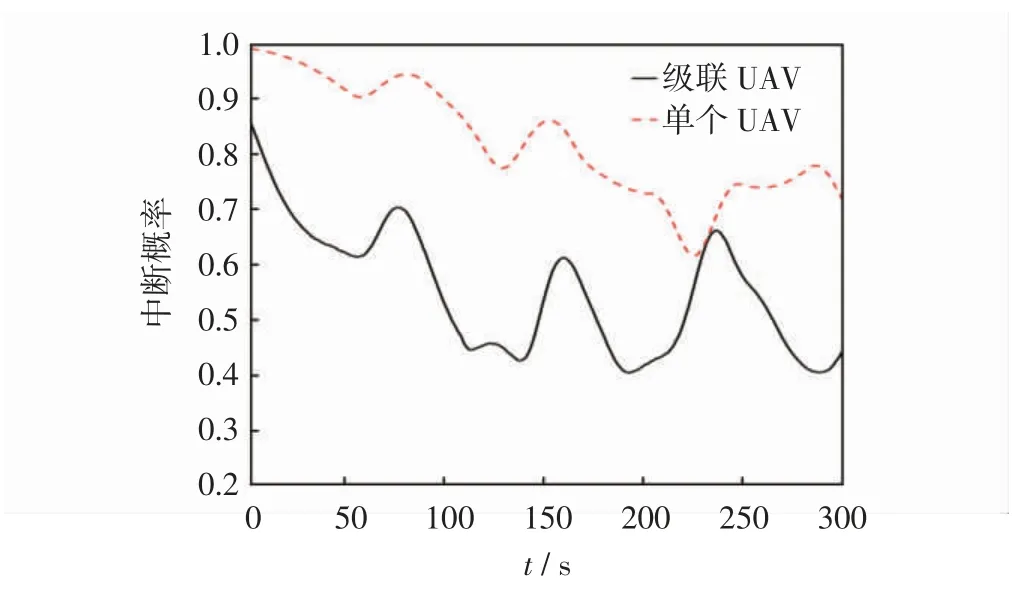
图7 不同方案下的系统中断概率Fig.7 Outage probability of UAV system with different plans

5 结语

针对UAV 级联中继通信系统飞行航迹的优化问题，给出了级联UAV 航迹联合优化方法与分步优化方法。研究结论如下：①级联UAV 航迹的联合优化方法与分步优化方法性能一致；②当移动接入节点运动时，为保证UAV 级联中继通信系统性能最优，与移动接入节点距离较近的UAV 将快速跟踪接入节点位置改变，而与固定基站距离较近UAV 位置改变较缓慢；③最大转弯角有利于提升UAV 级联中继通信系统的中断性能。