基于LS-DYNA的三维翼伞参数化建模仿真研究

许望晶 滕海山

（北京空间机电研究所，北京 100094）

0 引言

翼伞是根据飞机翼型产生升力的原理制作的一种降落伞，具备优良的滑翔性能、良好的稳定性和操纵性，可用于人员空降、航天器回收、无人机着陆、武器装备精确空投等多种应用领域，是回收着陆专业很有发展前途的一种型式[1]。

翼伞气动性能的研究一直是翼伞研究的热点和难点。美国从20 世纪60 年代开始对翼伞进行了大量风洞试验研究[2]，并于 80 年代做了大量空投试验，进一步推动了翼伞技术的发展。随着计算机技术和计算流体力学的飞速发展，对翼伞进行数值仿真研究越来越深入。Mittal等对带前缘切口的二维翼型剖面进行了数值模拟，得到了不同雷诺数下的升阻特性[3-4]；Mohammadi和Johari用Fluent软件分析了Clark Y二维翼型的气动特性，考虑了前缘切口，但未考虑柔性，并给出了内外流场特点[5-6]；C. Ibos等利用SINPA（numerical simulation of parachutes）软件采用非结构化网格的方法对三维翼伞的工作过程进行了数值模拟[7]，得到了绕伞衣工作时的速度、压力分布情况；李扬对二维翼伞剖面进行了模拟[8]，研究了翼伞非定常气动特性和表面涡脱落的周期性变化，所采用的计算模型未考虑前缘切口和翼伞的柔性；李健针对二维翼型剖面研究了切口角度和高度对翼型剖面气动特性的影响[9]，模型未考虑翼型的变形及翼型的内压；韩雅慧研究了有切口无气室、有气室无小孔和有气室有小孔3种翼伞表面光滑情况下以及翼伞表面不光滑处理后的气动力特性及绕流流场[10]，但是未考虑翼伞的柔性。朱旭等计算了翼伞平面形状对翼伞气动性能的影响，详细分析了翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响[11-12]，翼伞模型均未考虑翼伞的柔性变形。

由于翼伞柔性结构大变形的高度非线性和周围空气流场的高度复杂性，目前国内尚无系统的气动力数据库可供参考，同时国内对翼伞气动力的研究还非常少，而且大部分局限在二维翼型剖面，三维数值仿真的成果也不多，且基本上把翼伞伞衣当成刚性处理，更没有形成翼伞参数化设计流程。虽然LS-DYNA在降落伞的流固耦合仿真中应用较多，但由于翼伞结构以及受力情况的复杂性，在国内外公开的文献中很难找到使用LS-DYNA对翼伞进行气动性能仿真的相关研究。本文尝试建立翼伞参数化建模流程，使用LS-DYNA对翼伞进行流固耦合仿真获得其气动性能参数，并与试验数据进行对比。

本文结合翼伞的设计流程[13]，基于APDL（ANSYS Parametric Design Language）语言对翼伞进行参数化几何建模，生成带前缘切口的翼伞三维几何模型，并自动划分网格生成有限元模型，再利用LS-DYNA求解器进行流固耦合求解，并在仿真求解中考虑了伞衣柔性，因而获得更准确的翼伞气动性能参数。同时为了使整个仿真过程尽量简洁、便捷，基于MATLAB的GUI（Graphic User Interface）模块开发了集成平台的图形用户界面，从而提高了仿真的品质和工作效率。

1 翼伞稳态仿真

冲压式翼伞的典型工作过程包括充气、稳定滑翔和机动降落三个步骤[14]，其中绝大部分的工作时间处于稳定滑翔阶段，因此翼伞在这个阶段的气动力特性是翼伞总体设计的重点，若能通过仿真获得该阶段翼伞的气动力参数，将为翼伞总体设计提供重要依据。因此针对这一阶段进行翼伞仿真流程的初步构建，在此基础上利用该流程对数值算法的关键参数进行调整和优化，形成具有较强稳定性和可靠度的翼伞仿真流程，获得翼伞的气动性能参数，为翼伞总体设计提供了借鉴和依据。

将通用仿真流程[15]应用在翼伞仿真进行优化后，得翼伞仿真流程如图1所示。

图1 翼伞仿真流程Fig.1 Parafoil simulation flow chart

1.1 模型假设与初、边值条件

翼伞稳降速度在周围大气参数不发生变化的条件下是定值，因此可利用低速风洞模拟翼伞在这种状态下的运动过程，进而可设置合适的仿真参数来对相应风洞试验进行仿真模拟，在稳态仿真中，参照风洞试验的常见装配方式直接将伞绳端点固定在流场中。

对于翼伞结构建模，本文采用简化合并的思路，将翼伞上下翼面及翼肋这一类面积较大的织物结构抽象定义为伞衣结构，材料属性简化为双向异性的复合材料薄膜结构，保留伞衣加强带，伞绳简化为上下支伞绳和上下支操作绳，其材料属性都简化为单向受拉的索结构。

翼伞稳态阶段的速度远低于声速，因此整个流场仿真的速度区间为低速段，可采用不可压缩流场进行模拟。流场设计为长方体，流体入口面和出口面分别设置为压强入口和压强出口，都具有恒定的状态参数值，同时在出口面添加无反射约束，用于模拟远场状态。稳态仿真是对风洞试验的模拟，考虑到仿真试验具备消除壁面对流体剪切作用的功能，能使仿真结果与翼伞置于无限大流场的情形更为接近，因此将流场的壁面设置为滑移、无反射条件。流场域初速度统一设置为入口处约束速度值的流场初始条件设置方法，即保持流体入口面一直有一个恒速的来流。

1.2 几何建模

1.2.1 参数化几何建模设计模块

对翼伞进行几何建模首先需要确定翼伞的翼型，本模型翼伞的翼型采用Clark-Y型[16]。为了方便对翼伞模型进行修改，本文基于APDL语言对翼伞进行参数化几何建模。

（1）翼伞的基本参数

翼伞基本参数有：翼伞名义面积S，展弦比A，绳展比r，窄气室的个数Nn和宽气室的个数Nw，上翼面窄、宽气室的宽度Wn和Ww，翼伞安装角φ。翼伞模型的弦向和展向示意如图2～3所示，图中R为伞绳特征长度，ai、bi、ci、di、ei、fi、gi、hi、ki、li为翼伞几何建模中的关键点。通过这些关键点连成线，再形成面，即可建立起翼伞的几何模型，根据这些关键点、线、面的几何关系进行有规律的编号，便可形成参数化建模。

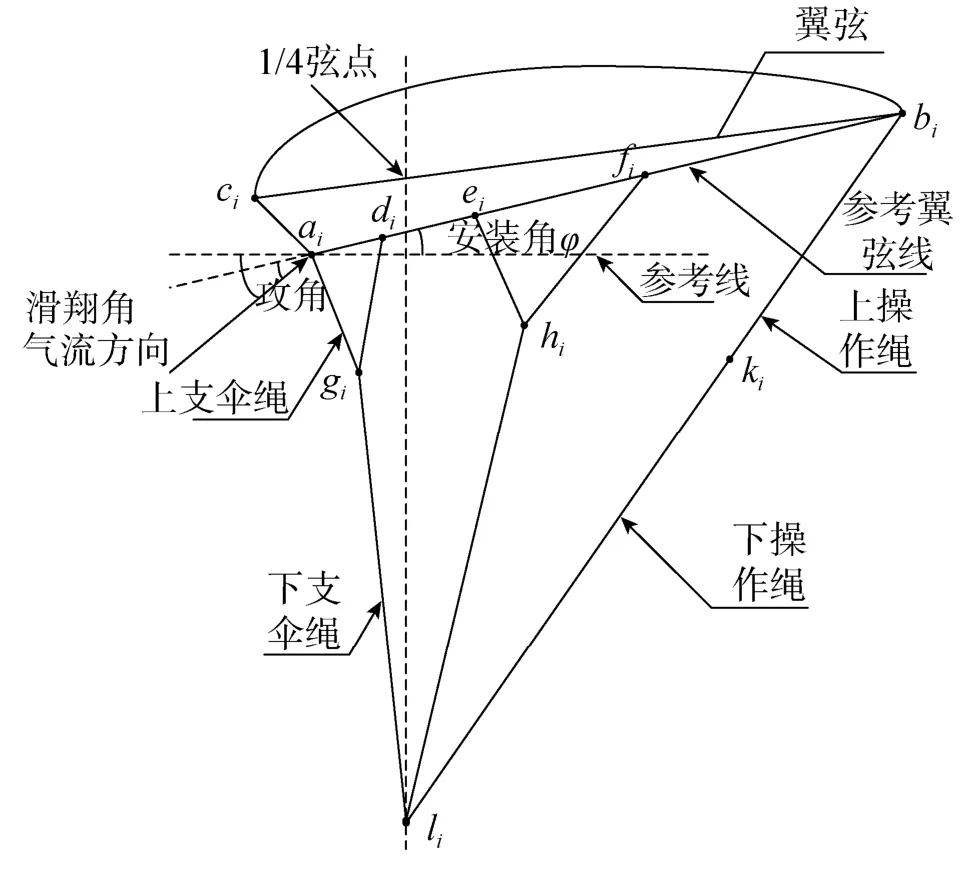
图2 翼伞弦向示意Fig.2 The parafoil chordwise diagram

图3 翼伞展向示意Fig.3 The parafoil spanwise diagram

翼伞最边上翼肋与中间对称翼肋的夹角θ为：

式中 R1为伞绳交汇点与上翼面的垂直距离。

相邻窄气室间的夹角ε为：

相邻半宽气室间的夹角γ为：

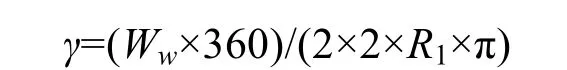
通过上面的参数以及几何关系可算出图中翼伞翼肋上各点的坐标值。

（2）伞衣加强带参数

伞衣加强带参数包括：上翼面加强带的个数、下翼面加强带的个数、上翼面加强带距上翼面前缘点的距离占整个上翼面线的比例、下翼面加强带距下翼面前缘点的距离占整个上翼面线的比例（不包括翼伞上下翼面前后缘的加强带）。

（3）伞绳及操纵绳相关参数

伞绳及操纵绳相关参数包括：上下支伞绳交汇点距下翼面的距离、上下支操作绳交汇点距下翼面的距离、上支操纵绳的个数、相连接气室的编号以及相连接的最大气室编号。

基于以上的设计模块，明确了翼型以及相关的翼伞参数，便可以通过APDL命令流采用自底向上的建模方法编写翼伞参数化几何建模程序，即从关键点开始依次建立模型的点、线、面和体。整个过程的关键和难点在于规划好各结构占用的系统资源，即模型中点、线、面和体的编号以及编号与翼伞参数之间的关系，以实现对这些结构的高效调用[17]。

本参数化翼伞模型是基于Clark-Y翼型进行建模的，翼肋开孔，小型翼伞气室宽度相等，而大型翼伞为防止两端气室塌陷，一般两端为窄气室，中间为宽气室，对大小型翼伞的这点区别在编程中进行了考虑。参数化翼伞模型窄气室个数与两倍宽气室个数的和不超过100，伞绳沿弦向的排数不超过5排。在建模过程中要注意模型点、线、面编号的分配，编号要有规律，以便于程序的调用和修改，编号与翼伞参数之间的关系一定要准确，不然无法进行参数化建模，不同组编号的最大空间要留足，以免出现编号混乱导致调用编号出错使参数化建模失败。

基于以上参数化设计，通过修改输入参数可以很快地得到大型翼伞、中型翼伞和小型翼伞和相应流场的有限元模型。

1.3 网格划分

网格划分的工作包括：设定材料类型、单位类型和单元形参；指定几何结构划分参考密度；生成固体域和流体域网格。设定好网格划分参数，计算网格便能通过程序自动生成。此外需要注意的是任意拉格朗日–欧拉（arbitrary lagrangian eulerian，ALE）耦合方式要求流场网格尺寸需与伞衣网格尺寸相匹配，两者不能有太大区别。将建立好的网格输出为关键字（Keyword，K）文件格式，然后就可进行下阶段关键字处理的工作。

1.4 关键字处理

Pre-Post是一款专门用于关键字处理的软件，同时兼具较强的前、后处理功能，图形操作界面也较为友好，因此选为此次翼伞仿真关键字处理软件。

由于此前在划分网格的过程中，只能定义翼伞仿真所需关键字的部分信息，因此需要对网格划分后形成的关键字进行相应的处理，如对伞衣材料的修改、接触控制的修改以及流固耦合方式的选择等，这样便能形成完整正确的关键字，进行翼伞的仿真求解。

1.5 仿真求解

LS-DYNA能够模拟真实世界的各种复杂几何非线性（大位移、大应变）问题，使用ALE方法进行流固耦合求解，采用流固耦合算法模拟问题时，往往要对拉格朗日（Lagrange）算法中的固体结构进行约束，将固体结构的相关参数传递给流体单元，以实现力学参量的传递。固体结构的主要约束方法是罚函数耦合约束。对于罚函数约束而言，其原理[18]是耦合系数追踪Lagrange节点（固体结构，即从物质）和欧拉（Euler）流体物质（主物质）位置间的相对位移s，如图4所示。检查每一个从节点对主物质表面的贯穿，如果从节点不出现贯穿，就不进行任何操作；如果发生从节点对主物质表面的贯穿，界面力F就会分布到Euler流体的节点上，界面力的大小与发生贯穿数量呈正比，即

式中 Ki为基于主从节点质量模型特征的刚度系数。

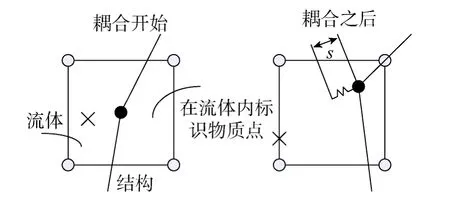
图4 罚函数耦合算法Fig.4 Penalty function coupled method

关键字文件调整后即可提交求解器进行求解，选用的求解器为LS-DYNA971版本。设置好求解所需的内存空间与调用线程数之后，对翼伞仿真模型的计算就可开始运行，最后的工作就是对求解结果进行处理，对翼伞稳态外形以及升阻力进行分析。

2 翼伞参数化设计、仿真平台

集成平台的图形用户界面基于MATLAB的GUI模块开发，包括“翼伞几何模型”、“建立有限元模型”、“关键字处理”以及“仿真求解”四个部分，每个部分只有在前置部分处理完成之后才能够被用户选取，可达到引导用户正确按照流程顺序进行设计、仿真的目的，并且都是在后台自动调用 LS-DYNA或者Pre-Post，从而避免了手动在不同程序之间的切换，使操作简洁，不易出错。

翼伞的仿真平台首先是基于以实际做试验的翼伞为仿真模型进行仿真计算，将仿真结果与试验数据进行对比，不断对数值算法的关键参数进行调整和优化，如图5所示。翼伞的几何模型尽量与实际翼伞，相符上下翼面加强带的位置应与翼伞伞衣网格划分数相匹配，否则由于加强带网格节点与伞衣网格节点没耦合上而导致加强带被吹飞；网格越小，网格单元越多，计算时间越长，为了兼顾仿真计算时间和计算精度，流场网格大小在计算机计算性能好的前提下尽量小，从而使仿真结果更加准确；关键字参数一定要齐全，边界条件、流固耦合参数、接触设置等要准确，与实际情况相符，否则很容易导致计算出错。在仿真流程优化后的基础上，通过修改翼伞的几何参数以形成不同工况下的翼伞模型并进行仿真（图 6所示），就能获得较准确的仿真结果。

3 三维翼伞参数化建模仿真实例

通过建立的翼伞参数化设计、仿真平台，在界面上修改输入参数就可以很快地建立翼伞的有限元模型，并利用LS-DYNA求解器进行仿真求解。本章以某中型翼伞为例，验证翼伞仿真流程的可行性和可靠性。

某中型翼伞，翼伞面积80m2,展长14.422m，弦长5.547m，17个气室，其中两端各2个窄气室，中间13个宽气室，该翼伞理论升阻比3.7，试验升阻比为3.1[19],理论最大升阻比时的稳态攻角为8°。考虑翼伞的柔性，不考虑翼伞的透气性，从以下三个角度对仿真结果进行分析。

翼伞伞衣的稳态外形图，从图7～9的对比可以发现，稳态时翼伞张开比较饱满，有鼓包，和实际试验时翼伞外形相差不大，总体来说比较符合实际情况。

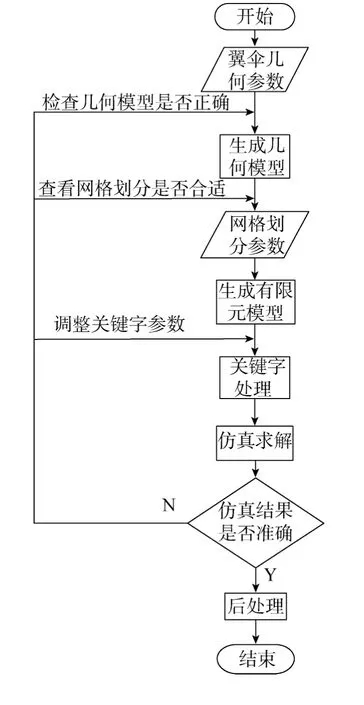
图5 翼伞仿真优化流程Fig.5 Parafoil simulation optimization flow chart

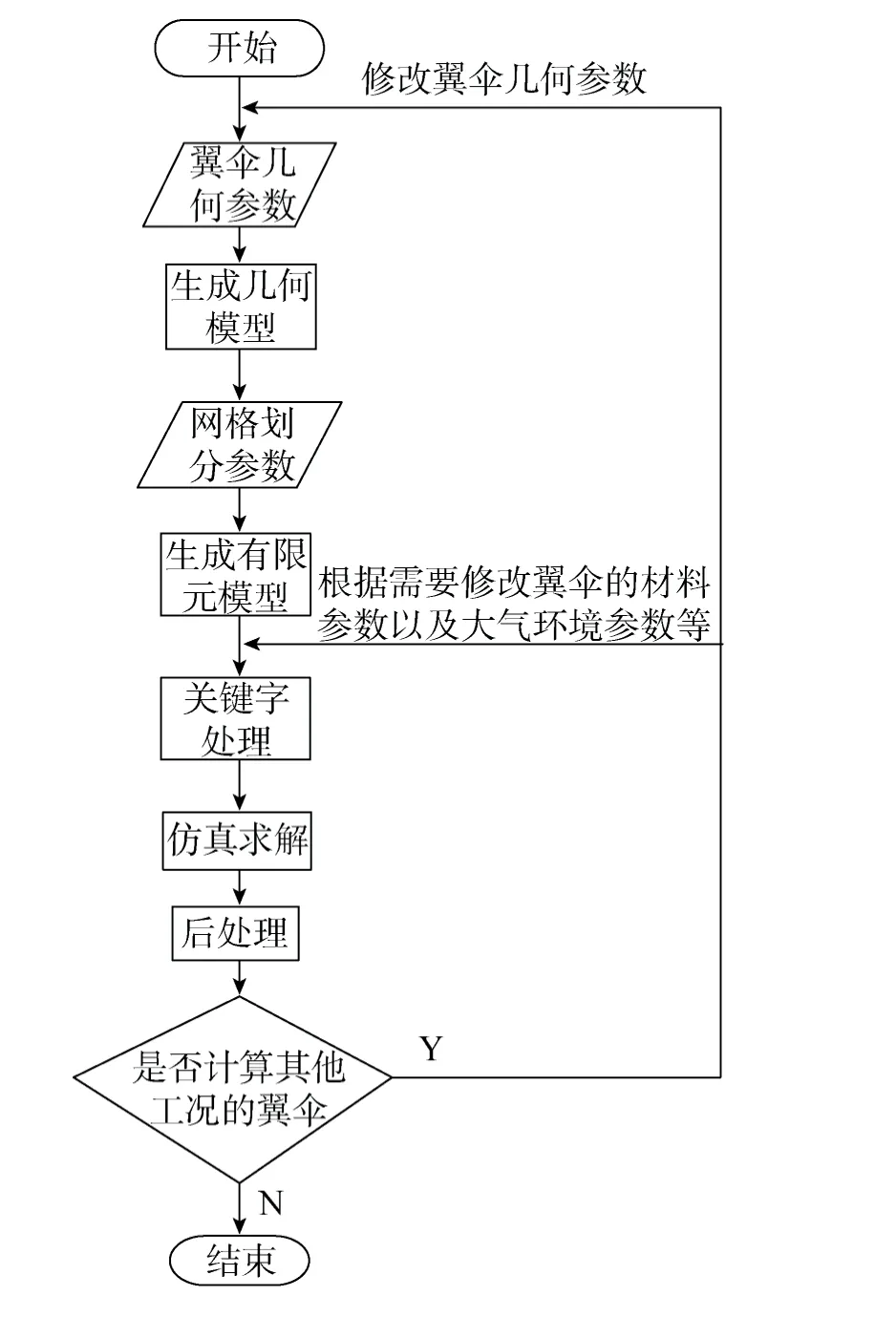
图6 不同工况翼伞仿真流程Fig.6 Parafoil simulation flow chart in different conditions

图7 翼伞初始外形Fig.7 The canopy initial shape

图8 翼伞稳态外形Fig.8 The canopy steady shape

图9 翼伞试验外形Fig.9 The canopy actual steady shape

翼伞攻角随时间变化如图10所示，翼伞从2.8s左右开始进入稳态，取其稳态段攻角的平均值，得翼伞稳态攻角为9.974 2°。

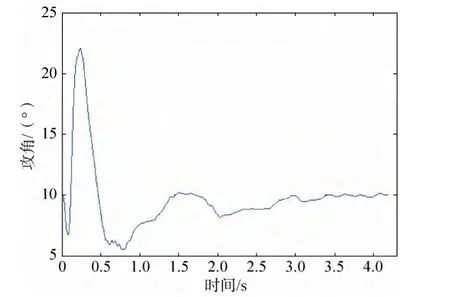
图10 翼伞攻角变化Fig.10 The angle of attack of parafoil variations

翼伞升阻力及其升阻比曲线如图11～12所示，翼伞从2.8s左右开始进入稳态，升力和阻力开始趋于稳定，取其稳态段的平均值得翼伞升力为13 654N，阻力为4 097.9N，升阻比为3.332 2。由于伞绳的直径很小，划分单元后特征尺寸也相应的小，如果要进行流固耦合计算，要求流体网格也相应的要小，大大增加了方程求解的运算复杂度和求解时间，同时伞绳单元与流场单元的耦合算法比较复杂；大多数商业流固耦合软件都不提供相关技术支持，故在翼伞的流固耦合仿真中没有考虑伞绳及回收物与流体的耦合；因此伞绳及回收物的阻力需要通过理论计算进行修正。根据《降落伞理论及应用》[20]中介绍的计算方法，以翼面积为参考面积的伞绳阻力系数CD1为：

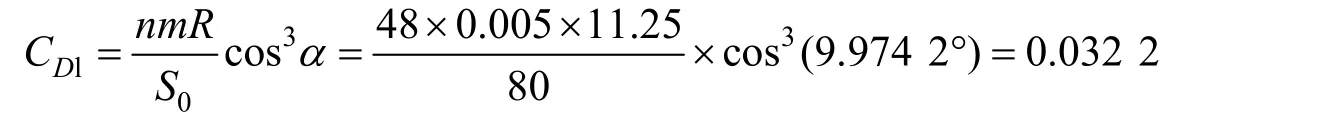
式中 n为伞绳数，上、下支伞绳按一支计算，伞绳36根，控制绳12根，共48根；m为伞绳的直径，取0.005m；R为伞绳特征长度，取11.25m；S0为翼伞名义面积，取80m2；α为翼伞的稳态攻角。

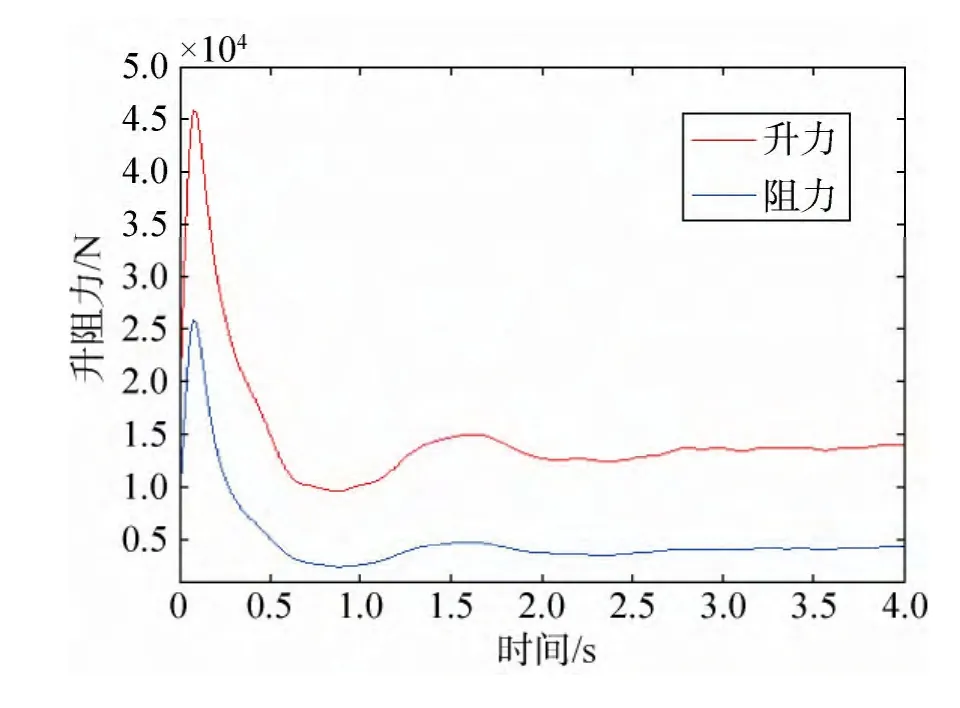
图11 翼伞仿真升阻力曲线Fig.11 The lift and drag curve of parafoil simulation

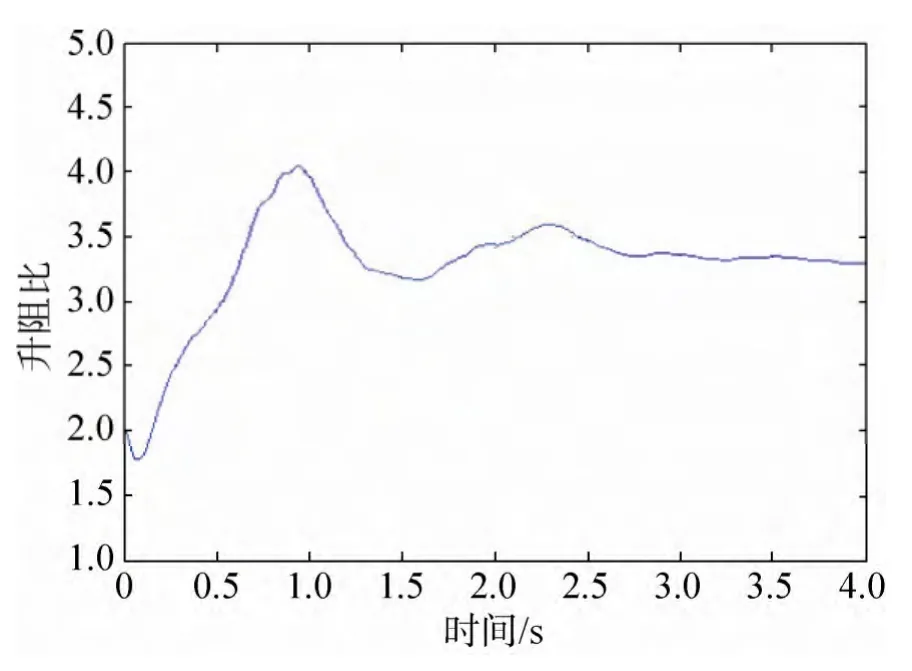
图12 翼伞仿真升阻比曲线Fig.12 The lift-drag ratio curve of parafoil simulation

以翼面积为参考面积的回收物阻力系数定义为CDs，回收物模型阻力面积按照0.6m2估算，因此CDs取为0.007 5。

所以经过修正之后的翼伞系统阻力D为

式中 ρ为大气密度，取1.18kg/m3；V为风速，取22m/s。故修正之后的翼伞升阻比为2.73，与试验翼伞升阻比的误差为11.87%。

总体来说，利用LS-DYNA仿真翼伞的稳态过程，所得翼伞气动数据符合实际情况，但也存在一些问题，如升力误差还较大，这可能与翼伞的模型简化、不考虑翼伞的透气性、模型网格划分细密以及关键字参数设置有关，在后续工作中需要相应改进和完善；其次LS-DYNA在流固耦合计算中没有考虑湍流的影响，这在一定程度上也影响了升力和阻力的值。

4 结束语

本文结合翼伞的设计流程和仿真流程构建了翼伞参数化三维几何建模和仿真于一体的设计仿真平台，并将仿真结果与试验数据进行了比较，经过验证，仿真方法切实可行，这极大地提高了相关问题研究的工作质量和效率，也为后续的研究工作和回收着陆一体化仿真试验平台的建立打下了基础。相对于翼伞的二维仿真以及把伞衣当成刚性的三维仿真研究，本文不仅是对翼伞三维模型进行仿真，而且在仿真求解时考虑了翼伞的柔性，仿真过程更符合翼伞试验的实际情况，所得翼伞稳态外形、稳态攻角以及升阻比与试验数据相符合，精度有很大提高，并形成了翼伞参数化三维几何建模和仿真于一体的设计仿真平台，大大提高了翼伞仿真效率，为三维翼伞的气动性能仿真研究提供了一定的借鉴和参考。后续工作可以通过调整网格划分细密和关键字参数设置进一步提高仿真的精度，并在平台的基础上改变翼伞的安装角和绳展比进行仿真研究，找出安装角或绳展比对翼伞气动性能的影响规律。

（

）

[1] 王希季. 航天器进入与返回技术（上）[M]. 北京: 中国宇航出版社, 1991. WANG Xiji. The Technology of Spacecraft Entry and Return （a） [M]. Beijing: China Astronautics Press, 1991.

[2] Nicolaides J D, Tragarz M A. Parafoil Flight Performance[R]. Air Force, 1971.

[3] Mittal S, Saxena P, Singh A. Computation of Two-dimensional Flows Past Ram-air Parachutes[J]. International Journal for Numerical Methods in Fluids, 2001, 35: 643-667.

[4] Balaji R, Mittal S, Rai A K. Effect of Leading Edge Cut on the Aerodynamics of Ram-air Parachutes[J]. International Journal for Numerical Methods in Fluids, 2005, 47: 1-17.

[5] Mohammadi M A, Johari H. Computation of Flow over a High-performance Parafoil [C]. 20th AIAA Aerodynamic Deceleration Systems Technology Conference and Seminar. Washington: AIAA. 2009: 1-9.

[6] Mohammadi M A, Johari H. Computation of Flow over a High-performance Parafoil Canopy[J]. Journal of Aircraft, 2010, 47（4）: 1338-1345.

[7] Ibos C, Lacroix C. Fluid-structure Simulation of a 3D Ram Air Parachute with SINPA Software[R]. AIAA-1999-1713, 1999.

[8] 李扬. 冲压式翼伞后缘下拉特性的数值研究[D]. 长沙: 国防科技大学, 2004. LI Yang. Numerical Simulation of Ram-air Parachute with Flap Deflection[D]. Changsha: National University of Defense Technology, 2004. （in Chinese）

[9] 李健. 前缘切口对冲压式翼伞的气动力影响[J]. 航天返回与遥感, 2005, 26（1）: 36-41. LI Jian. The Aerodynamic Influence of the Cutter of the Front Edge of Parafoil[J]. Spacecraft Recovery and Remote Sensing, 2005, 26（1）: 36-41. （in Chinese）

[10] HAN Yanhui. Aerodynamics Simulation of a Large Multi-cells Parafoil[C]. 20th AIAA Aerodynamic Deceleration Systems Technology Conference and Seminar. Washington: AIAA. 2009: 1338-1345.

[11] 朱旭, 曹义华. 翼伞平面形状对翼伞气动性能的影响[J]. 航空学报, 2011, 32（11）: 1998-2007. ZHU Xu, CAO Yihua. Numerical Simulation of Planform Geometry Effect on Parafoil Aerodynamic Performance[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32（11）: 1998-2007. （in Chinese）

[12] 朱旭, 曹义华. 翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响[J]. 航空学报, 2012, 33（7）: 1189-1200. ZHU Xu, CAO Yihua. Effects of Arc-anhedral Angle, Airfoil and Leading Edge Cut on Parafoil Aerodynamic Performance[J] . Acta Aeronautica et Astronautica Sinica, 2012, 33（7）: 1189-1200. （in Chinese）

[13] 林仙友. 高翼载冲压式翼伞的设计技术[J]. 航天返回与遥感, 1993, 14（3）: 16-23. LIN Xianyou. The Design of High Wing Loading Ram-parafoil [J]. Spacecraft Recovery & Remote Sensing, 1993, 14（3）: 16-23. （in Chinese）

[14] 韩雅慧. 空投系统仿真关键问题研究[D]. 北京: 北京航空航天大学, 2013. HAN Yahui. The key Problems Research of Airdrop Simulation[D]. Beijing: Beijing University of Aeronautics & Astronautics, 2013. （in Chinese）

[15] 贾贺, 荣伟, 陈国良. 基于LS-DYNA软件的降落伞充气过程仿真研究[J]. 航天器环境工程, 2010, 27（3）: 367-373. JIA He, RONG Wei, CHEN Guoliang. A Simulation Research of Parachute Inflation Process Based on LS-DYNA [J]. Spacecraft Environment Engineering, 2010, 27（3）: 367-373. （in Chinese）

[16] 吴卓. 冲压式翼伞翼型剖面气动特性数值模拟[C]. 第二十三届全国空间探测学术交流会. 厦门: 2010. WU Zhuo. Numerical Simulation of Parafoil Airfoil Profile Aerodynamic Characteristic[C]. The 23rd National Academic Conference of Space Exploration. Xiamen: 2010. （in Chinese）

[17] 甘和麟. 环帆伞阻力特性及其尺寸效应的研究[D]. 北京: 中国空间技术研究院, 2014. GAN Helin. Analysis of Ringsail Drag Characteristics and Scale Effects [D]. Beijing: China Academy of Space Technology, 2014. （in Chinese）

[18] John O H. Theoretical Manual [M]. USA: Livermore Software Technology Corporation （LSTC）, 1998.

[19] 吴卓. 一种冲压式翼伞数值仿真与优化[C]. 第二届进入、减速与着陆（EDL）技术全国学术会议. 南京, 2014. WU Zhuo. The Numerical Simulation and Optimization of the Parafoil[C]. The 2rd National Academic Conference of EDL. Nanjing, 2014. （in Chinese）

[20] 王利荣. 降落伞理论及应用[M]. 北京: 宇航出版社, 1997. WANG Lirong, Parachute Theory and Application[M]. Beijing: China Astronautic Press, 1997. （in Chinese）