空间红外遥感相机制冷机微振动对MTF影响分析

王跃 王博 刘世平 李世其 熊琦

（1 北京空间机电研究所，北京 100094）

（2 华中科技大学机械学院，武汉 430074）

0 引言

空间遥感相机光学系统中的光学元件在微振动载荷的作用下会产生刚体位移和表面变形，光学元件刚体位移会导致光学系统产生慧差、像散和离焦，表面变形将影响光学系统的波前差。光轴偏转会导致像移引起成像模糊，这些都会影响相机的成像品质[1]。

空间红外遥感相机内部主要扰动源是为红外焦面探测器提供低温保障的制冷机。对于工作在红外波段的遥感相机，红外焦面需要在低温环境下工作，以降低焦面探测器的热噪声，提高灵敏度。目前国内外通常采用低温制冷机冷却红外焦平面，以保证其在低温范围内正常工作。制冷机工作时由于活塞等运动部件动量不平衡、高压气体压力波动等产生干扰力，影响光学系统的分辨率和指向精度等。

理想的镜面是光滑的，而有限元方法得到的是离散的数据，将离散数据拟合成光滑连续曲面需要采用合适的拟合方法。Zernike多项式作为曲面拟合的常用方法，以其特有的优点使其成为结构分析和光学分析之间的桥梁[2]。

相机在正常工作条件下，受到来自相机内部以及卫星平台活动部件微振动载荷的扰动。由于主镜、次镜尺寸较大，结构刚性相对较小，产生的刚体位移和面形变化会对相机的成像品质起主要影响，而分色片及透镜口径小、刚度高，稳定性好，微振动对镜片的刚体位移和面形影响很小。本文主要以主、次镜为对象来分析微振动对成像品质的影响。

1 相机有限元模型建立

空间遥感相机在轨工作时，影响光学元件精度的因素主要有以下方面：1）光学元件在加工过程中产生的面形误差和镜头装调误差；2）光学元件在振动源的扰动下发生偏移产生刚体位移；3）光学元件在振动源的扰动下发生面形的变化。本文只分析振动源扰动引起的光学元件刚体位移和面形变化。根据制冷机微振动测试分析结果，制冷机在工作时产生频率约为0～500Hz的扰动力（图1是制冷机测点测试信号在X轴方向的扰动力频谱，项目测试要求采样频率不低于2 000Hz），幅值范围0～1.5N。

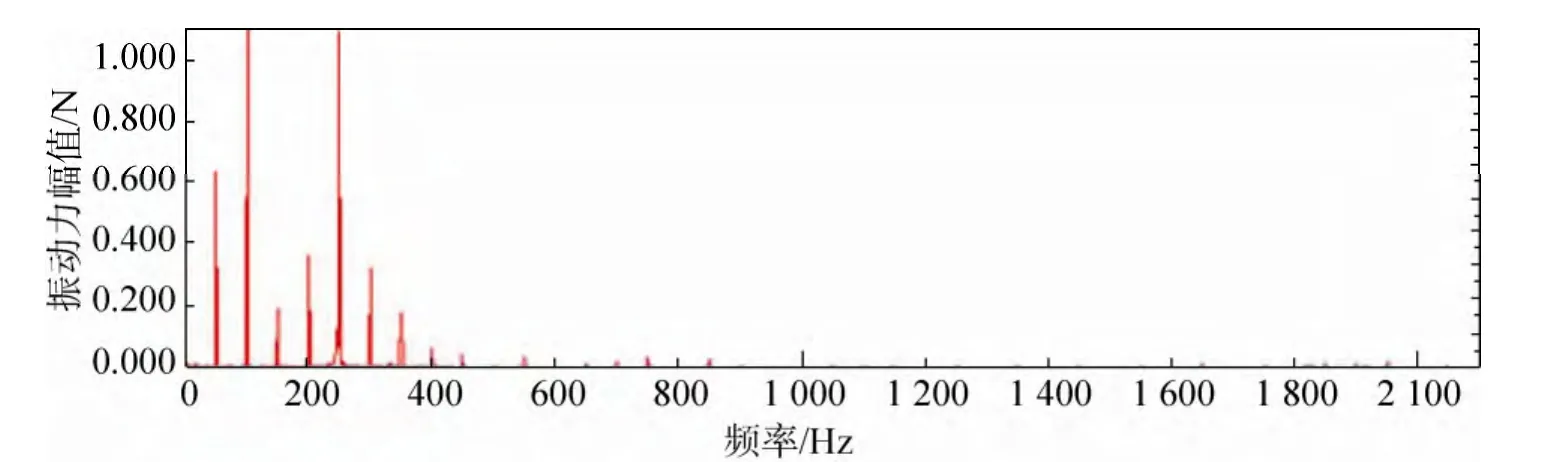
图1 制冷机测试扰动力频谱Fig.1 Disturbance force’s frequency spectrogram of cryocooler test

由制冷机扰动力频谱分析可知，扰动力是以 50Hz为基频的一系列谐波信号，可以用式（1）来描述[3]

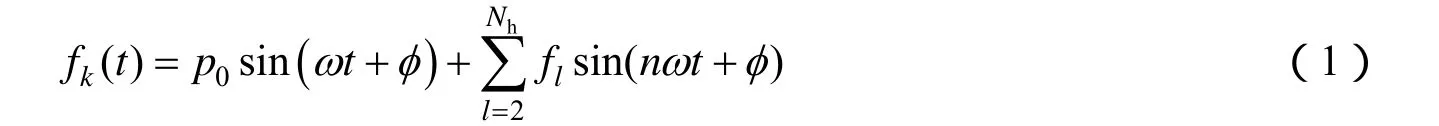
式中 fk为制冷机测试信号；P0为制冷机工作频率幅值；ω为制冷机驱动频率；t为时间；fl表示第 l阶谐波幅值；Nh为扰动谐波数；φ为相位角。

借助有限元方法，将连续的振动系统划分成n个自由度系统，空间遥感相机的动力学模型可以表示为

式中 m为n阶对称质量矩阵，c为n阶对称阻尼矩阵，k为n阶对称刚度矩阵；n×1维列向量⋅x⋅（t），x⋅（t），x（t）分别代表系统的广义加速度、速度和位移；F（t）为表示系统激励的n×1维列向量。通过测得的系统激励对式（2）进行求解，得出光学镜片节点的位移矩阵并进行面形分析计算。

某空间遥感相机光学系统构型如图2所示，光线由主镜、次镜反射，经由分色片、透镜组到达成像焦面。运用 hypermesh软件建立有限元模型，加载制冷机振源载荷，获得相机主次镜的整体变形如图 3所示，可以看出主镜次镜除了产生刚性位移偏离了理想安装位置（包括平移和倾斜），面形也发生变化，光轴也发生了偏转。选取主镜响应最大时间点的节点坐标作为曲面拟合与分析的有限元数据，表1为主镜节点坐标和变形量。

图2 某空间遥感相机光学系统构型Fig.2 A space remote sensing camera’s optical system configuration

图3 相机主次镜的整体变形云图Fig.3 Overall deformation of primary and second mirror in camera

表1 主镜有限元节点坐标及变形Tab.1 Primary mirror’s finite element node coordinates and displacements mm

2 镜面拟合与分析

要将有限元方法计算得到的离散数据拟合成光滑连续曲面需要采用合适的拟合方法。主次镜的整体变形对应的是波前像差的变化，主要包含平移、倾斜、离焦、像散等，其中平移和倾斜是刚性位移，离焦、像散等主要是面形的变化。可以通过Zernike多项式拟合的方式分离刚性位移和面形变化[4]。

有限元计算输出文件包括节点变形前坐标（x,y,z）和变形量（Δ x ,Δ y ,Δ z ），见表 1。将有限元计算文件数据带入n项Zernike多项式可得线性方程组（3），

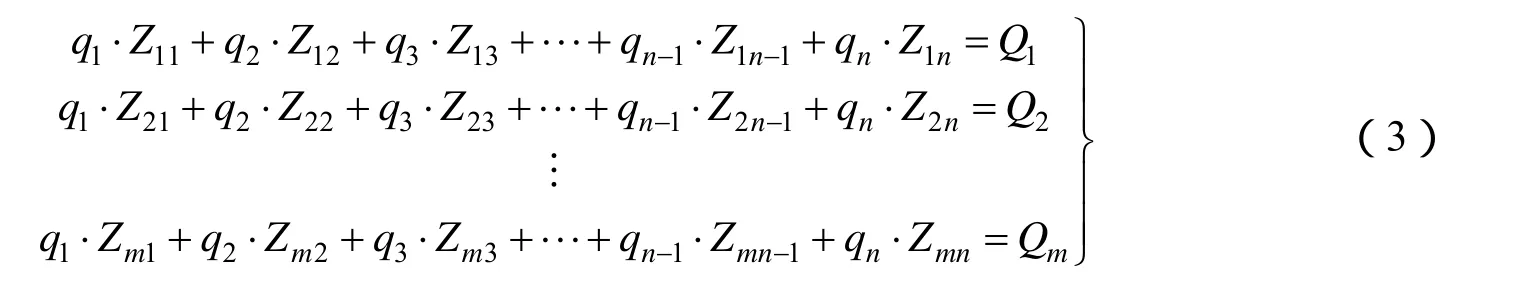
写成矩阵形式：

式中 Z=（Zij）为m×n矩阵，其中i为节点数，Zj（xi,yi）为Zernike多项式的第j项；表示经多项式拟合后的结果数据；为n项Zernike多项式系数。

选取Zernike多项式的前37项作为一组基拟合波面，将镜面变形后的节点数据代入拟合公式（3），镜面有限元划分节点数远远大于未知数的数目，得到的线性方程为矛盾方程，矛盾方程不存在通常意义下的解，一般通过最小二乘法来获得的最小二乘解。通过MATLAB计算获得Zernike多项式前37项系数，如表2所示。

表2 主镜次镜Zernike多项式拟合系数Tab.2 Zernike polynomials fitting coefficient of primary and second mirror

Zernike多项式的前三项分别对应着刚性位移、X轴倾斜及Y轴倾斜。由表2中的Zernike系数可以看出前三项系数要远远大于后面的系数，表明扰动力对主次镜的刚性位移影响较大，对镜面面形影响较小。

通过Zernike拟合得到变形后的主镜面形，如图4所示，变形量约为为100nm。图5是去除刚性位移后的主镜面形变化，变形量约为3nm。显而易见，微振动导致的主镜刚性位移是影响波前像差的主要因素。

拟合得到变形后的次镜面形如图6所示，变形量约为10nm。图7是去除刚性位移后的次镜面形变化，变形量约为1.0×10–2nm。由此可知，微振动导致的次镜面形变化可以忽略。

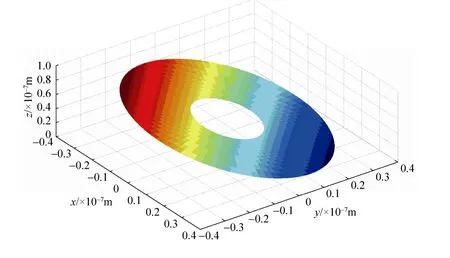
图4 变形后的主镜面形Fig.4 Primary mirror surface after deformation

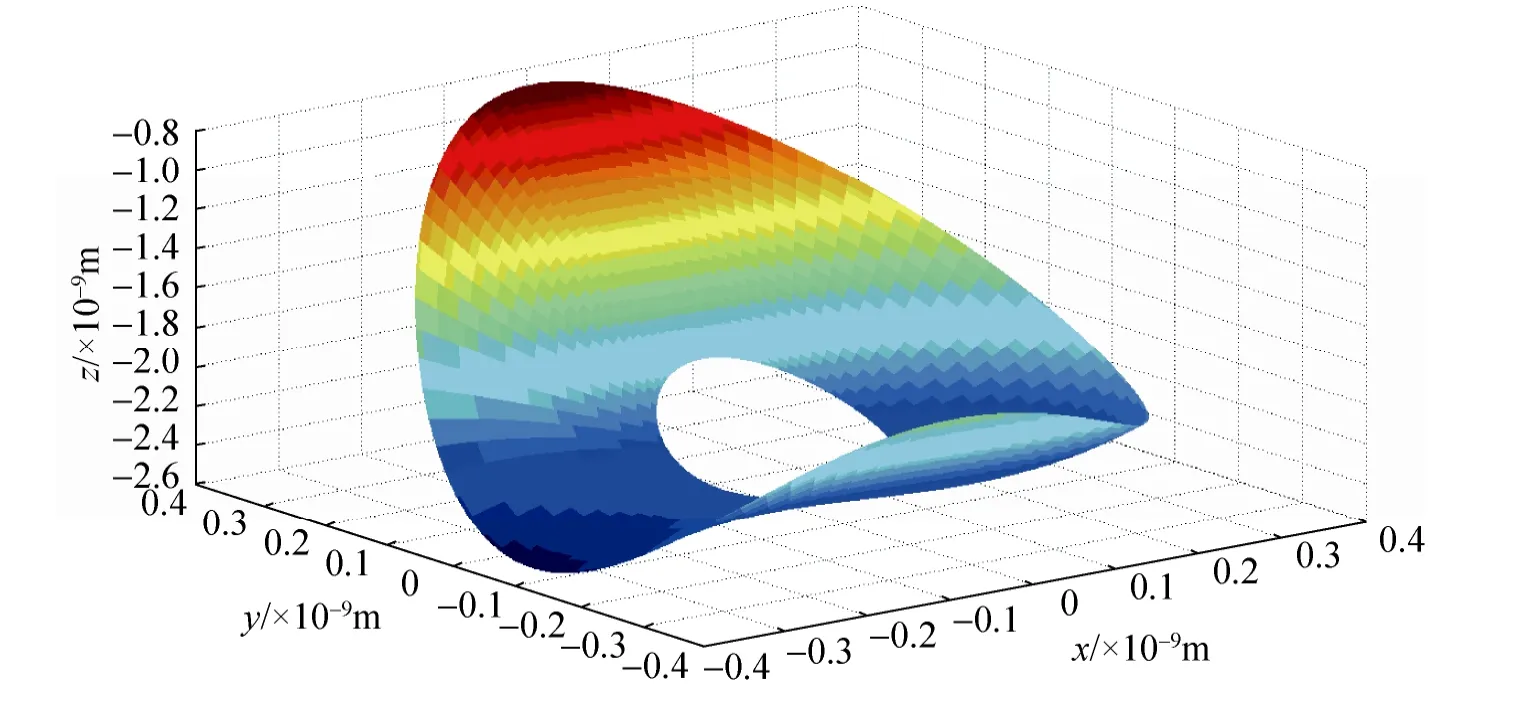
图5 去除刚性位移后主镜面形Fig.5 Primary mirror surface without rigid-body motion

图6 变形后的次镜面形Fig.6 Second mirror surface after deformation

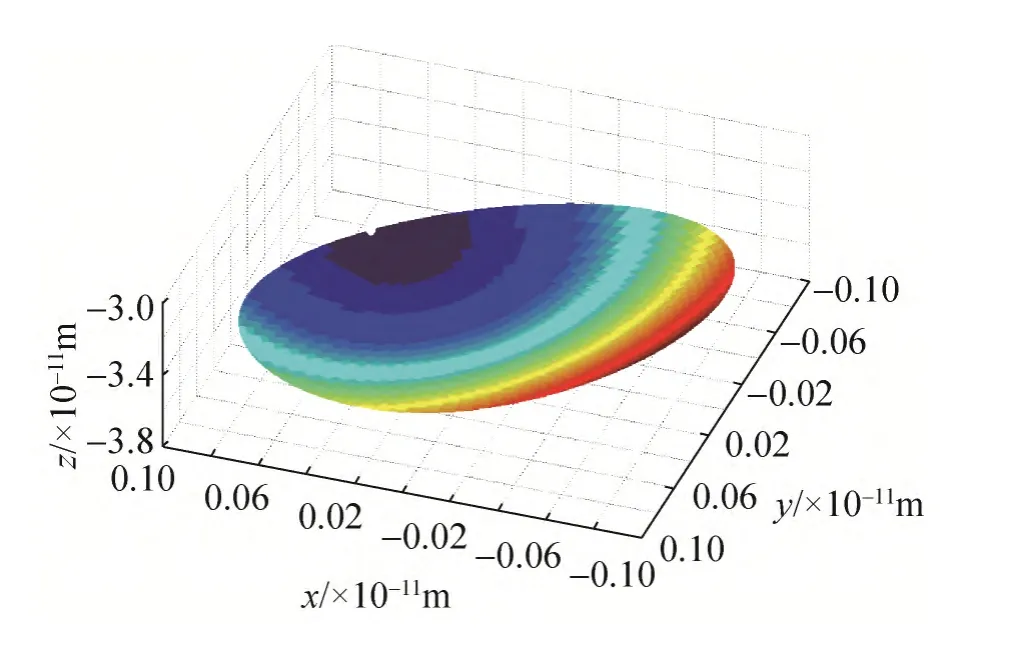
图7 去除刚性位移后次镜面形Fig.7 Second mirror surface without rigid-body motion

光学元件面形误差通常采用镜面表面最大峰谷（PV）值和镜面表面形貌的均方根误差（RMS）值来表示。PV值计算公式为

RMS体现了波面的变化缓慢，计算公式为

式中 di为节点i到拟合波面的法向距离；为节点到拟合波面的平均法向距离；N为波面拟合计算节点数目。

主次镜PV和RMS计算结果见表3。主次镜的面形变化很小，微振动扰动对主次镜的影响主要体现在刚性位移。

通过主次镜面形的分析可知，对于空间遥感相机在轨振动，光学元件的刚性位移远远大于面形的变化。主镜、次镜的固有频率分别在1 200、3 000Hz以上，对于频率范围0～500Hz的扰动力激励，主次镜自身的变形量（即镜面变形）很小。因此，刚性位移的变化是需要着重考虑的因素。

表3 主次镜PV和RMSTab.3 Primary and second mirror’s PV and RMS nm

3 振动对相机调制传递函数的影响

调制传递函数（MTF）能反映成像系统对目标不同空间频率的传递特性[5]，是常用的光学系统成像品质评价工具[6]。光学元件偏离理想安装位置会影响相机光学传函的变化，将空间相机光学元件在制冷机微振动作用下的曲面拟合结果代入Zemax软件计算MTF的结果，如图8及表4所示（图8中T表示切向，S表示弧矢方向）。由表4的数据可以看出，光学元件偏离理想安装位置对MTF的影响非常小，对应归一化空间频率56线对/mm处MTF下降了0.001 5%。

图8 偏离理想安装位置前后的MTF曲线Fig.8 MTF curve of ideal position and changed position

表4 偏离理想安装位置前后的MTF值Tab.4 MTF value of ideal position and changed position

微振动造成相机光学元件发生刚性位移，光学元件的刚性位移会导致相机光轴发生偏角变化[7]。相机光轴绕X轴的偏角变化如图9所示，由于制冷机的工作频率为50Hz，相机为受迫振荡，可以看出光轴的振荡频率也为50Hz。

光轴空间偏角随时间的变化曲线如图10所示，偏角最大值为0.0371″。按式（7）计算由相机光轴变化引起的像移量，相机归一化空间频率对应的MTF计算由式（8）给出[8-10]。

式中 α为主光轴偏角；f为相机焦距；δ为像移量；fs为归一化空间频率。

图9 相机光轴绕X轴的偏角变化Fig.9 Camera optical axial angle rotating about X-axis

图10 光轴偏角随时间的变化Fig.10 Optical axial angle vs time

将α=0.037 1″，fs=56线对/mm，代入式（7）、（8）中，计算得到MTF下降量为0.41%。因此可知，光轴的偏角变化对相机的成像影响大于偏离安装位置对相机成像品质的影响。由于光轴偏角是随时间变化的，对 MTF的影响也是随时间变化的，当微振动载荷引起的偏角对相机MTF影响最大时，MTF下降量不超过0.41%，在工程可接受的范围内。

相机扰动力是以50Hz为基频的一系列谐波信号，单独提取出每个频率的幅值代入有限元模型计算，获得不同频率下的光轴偏角，如图11所示。由于相机的一阶固有基频为45 Hz，和制冷机基频接近，频率为50Hz的谐波信号对光轴的偏角影响最大，随着频率的提高，对光轴影响逐渐变小，频率大于250 Hz的谐波信号主要对应相机的某些局部模态，对相机的光轴偏角影响极小，由此引起的MTF下降量可忽略不计。

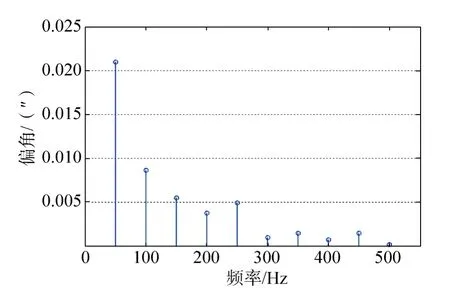
图11 不同频率激励下的光轴偏角Fig.11 Optic axial angle of different frequency

4 结束语

本文主要从相机微振动源分析入手，通过有限元方法对光学元件曲面拟合，面形、光轴分析，最后结合光学成像分析了空间红外遥感相机微振动对成像品质的影响。通过对微振动载荷激励下的镜面拟合分析可知，微振动对相机光学元件自身面形的影响很小，主要表现为光学元件刚性位移和光轴偏转。光学元件之间偏离理想位置的刚性位移造成MTF下降了0.001 5%，影响极其有限。相机微振动激励源主要为制冷机，其工作频率为50Hz，此频率下的的谐波信号对相机光轴偏角影响最大，引起的MTF下降量也最大，为 0.41%，经分析，MTF下降量在工程可接受的范围内。

（

）

[1] 丁延卫, 尤政, 卢锷. 航天光学遥感器光机结构尺寸稳定性变化对成像质量的影响[J]. 光学与光电技术, 2004, 2（3）: 1-4. DING Yanwei, YOU Zheng, LU E. Influences of Dimension Instability of Space Optical Remote Sensor Opto-structural System on Imaging Quality[J]. Optics & Optoelectronic Technology, 2004, 2（3）: 1-4. （in Chinese）

[2] 单宝忠, 王淑岩, 牛憨笨, 等. Zernike 多项式拟合方法及应用[J]. 光学精密工程, 2002, 10（3）: 348-322. SHAN Baozhong, WANG Shuyan, NIU Hanben, et al. Zernike Polynomial Fitting Method and Its Application[J]. Optics and Precision Engineering, 2002, 10（3）: 348-322. （in Chinese）

[3] De Weck O L, Miller D W. Integrated Modeling and Dynamics Simulation for the Next Gener-ation Space Telescope[D]. Massachusetts: Massachusetts Institute of Technology, 1999: 54-55.

[4] 杨佳文, 黄巧林, 韩友民. Zernike多项式在拟合光学表面面形中的应用及仿真[J]. 航天返回与遥感, 2010, 31（5）: 49-55. YANG Jiawen, HUANG Qiaolin, HAN Youmin. Application and Simulation in Fitting Optical Surface with Zernike Polynomial[J]. Spacecraft Recovery & Remote Sensing, 2010, 31（5）: 49-55. （in Chinese）

[5] 刘洋. 空间相机成像质量自动评价方法研究[D]. 长春: 中国科学院长春光学精密机械与物理研究所, 2011. LIU Yang. Research on Automatic Evaluation Method of Space Camera Image Quality[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Science, China, 2011. （in Chinese）

[6] 王红娟. 微振动对空间相机像质影响研究[D]. 西安: 中国科学院西安光学精密机械研究所, 2013. WANG Hongjuan. Research on Space Camera Image Degradation Included by Micro-vibration[D]. Xi’an: Xi’an Institute of Optics & Precision Mechanics, Chinese Academy of Sciences, 2013. （in Chinese）

[7] 刘涌, 胡永力. 动量轮微振动扰振频谱对三反同轴相机的影响[J]. 航天返回与遥感, 2014, 35（5）: 31-37. LIU Yong, HU Yongli. Effect of Momentum Wheel Jitter Spectrum on Three-mirror-anastigmatic Imaging[J]. Spacecraft Recovery & Remote Sensing, 2014, 35（5）: 31-37. （in Chinese）

[8] 徐鹏, 黄长宁, 王涌天, 等. 卫星振动对成像质量影响的仿真分析[J]. 宇航学报, 2003, 24（3）: 259-263. XU Peng, HUANG Changning, WANG Yongtian, et al. Modulation Transfer Function in Push-broom Camera Limits Resulting from Mechanical Vibration[J]. Journal of Astronautics, 2003, 24（3）: 259-263. （in Chinese）

[9] 赵鹏. 振动对航空相机成像质量影响的分析[J]. 激光与红外, 2001, 31（4）: 240-242. ZHAO Peng. The Vibration Analysis of Optical Instrument in Flying Platform[J]. Laser & Infrared, 2001, 31（4）: 240-242. （in Chinese）

[10] 张博文, 王小勇, 胡永力. 微振动对高分辨率空间相机成像影响的集成分析[J]. 航天返回与遥感, 2012, 33（2）: 60-66. ZHANG Bowen, WANG Xiaoyong, HU Yongli. Integrated Analysis on Effect of Micro-vibration on High Resolution Space Camera Image[J]. Spacecraft Recovery & Remote Sensing, 2012, 33（2）: 60-66. （in Chinese）