大型翼伞的三维气动性能分析

陆伟伟 张红英 连亮

（南京航空航天大学航空宇航学院，南京 210016）

0 引言

冲压式翼形伞（后统称翼伞）是近代发展起来的一种新型降落伞。与圆形降落伞利用空气阻力减慢物体在空气中的下降速度不同，它是一种由前缘切口进入空气，在气室内形成滞止压力以保持其伞衣形状的新型降落伞[1]。同时，翼伞可以通过伞绳的操纵来实现转弯动作，这种可控性和其自身的滑翔性能使得翼伞广泛应用于多个领域。

具有较高落点精度的可操控、适用于大质量回收物的大型翼伞是航天回收将来发展的重要方向。20世纪 60年代，美国就开始对翼伞进行了大量风洞试验研究[2]，80年代又做了大量空投试验，进一步推动了翼伞技术的发展。典型的美国X-38翼伞返回系统[3-4]，其最大的翼伞面积为700m2，回收物质量为11t。相对比国内，由于成本原因，对翼伞的风洞和空投试验开展的较少[5-6]。

进入21世纪以来，由于计算机软硬件技术的迅猛发展，数值模拟在时间和经济成本上有着越来越大的优势，国内外纷纷展开了对翼伞的数值模拟。文献[7-8]对二维带前缘切口的翼伞进行了数值模拟，得到了不同雷诺数下的升阻特性；文献[9]对带气室和不带气室的三维翼伞模型进行了初步的对比研究；文献[10]模拟了二维冲压翼伞的非定常气动特性，模拟了上表面涡脱落的周期性变化；文献[11]计算了前缘切口角度和切口高度对二维翼伞气动特性的影响；文献[12-14]计算了翼伞平面形状对翼伞气动性能的影响，详细分析了翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响以及气室对翼伞气动特性和结构变形的影响，同时得出翼伞三维流场的特点以及基于弱耦合方法得到的翼伞气动变形。文献[15]研究了翼伞的气动特性和飞行力学特性，计算得到了翼伞充气后的外形。

本文以某大型航天器部件的可控安全回收系统为研究背景，采用有限体积法求解K-epsilon二方程湍流模型下的 Navier-Stokes（N-S）方程，对该回收系统中的大型翼伞进行三维数值模拟，研究了滑翔阶段翼伞的升阻特性，同时对翼伞单侧后缘下拉情况下的气动性能进行初步分析，并比较了单侧后缘下拉与不下拉翼伞的升阻特性和力矩变化，为针对重型回收物可控回收设计的大型翼伞研究提供一定的参考。

1 计算方法和模型

完整的翼伞数值仿真难度很大，涉及到空气动力学、纺织材料结构力学、流固耦合等诸多复杂的问题。作为该型回收系统数值仿真中气动运算的一部分，本文偏重于翼伞的气动性能，因此可将其简化为空气动力学问题，其控制方程为N-S方程，通过求解该方程从而得到翼伞的气动参数。

1.1 控制方程

空气绕翼伞的流动满足N-S方程

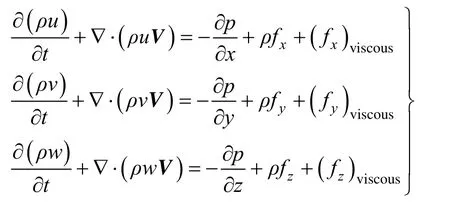
式中 ρ为大气密度；t为时间；V为速度；p为压强；x，y，z分别为笛卡尔坐标系下的三个方向；u， v，w为速度在x，y，z方向的分量；fx，fy，fz为彻体力在x，y，z方向的分量；为粘性力在x，y，z方向的分量。

1.2 仿真模型

冲压式翼伞是由伞衣、伞绳、操纵绳、稳定面、收口装置、吊带等组成。伞衣是由不透气的涂层织物制成的上、下翼面，中间联以具有翼型的肋片，伞衣前缘开有切口便于空气进入形成气室。肋片上开有通气孔，便于各气室间空气流通，保证伞衣迅速充气和各气室压力均匀。翼伞结构示意图如图1所示。图中，b为展长；b'为气室宽度；c为弦长；Ф为安装角；ε为切口角度；e为切口长度；Lsh为伞绳特征长度。

图1 翼伞结构示意Fig.1 The structure diagram of a parafoil

本文选用基于 Clark-Y翼型的改进翼伞，取其经流固耦合仿真方法得到的充满外形（即伞衣有鼓包的情况）作为研究对象。图2给出了该型翼伞的几何模型，单侧后缘下拉翼伞的三维模型如图3所示。该型翼伞充满外形的几何参数如下：展长b=39.3m；弦长c=13.76m；切口角度ε=43°；切口长度e=1.548m；单侧下拉翼伞的下拉处后缘点与未下拉时后缘点的距离约为1m。

图2 翼伞的充满外形Fig.2 The bulge appearance of the parafoil

图3 单侧后缘下拉翼伞Fig.3 The unilateral flap deflection parafoil

由于真实翼伞外形及气动特性的复杂性，本文主要针对充满翼伞的气动特性，因此对翼伞模型作以下假设：

1）翼伞模型为刚性模型；

2）不考虑伞衣厚度的影响，近似认为伞衣材料不透气；

3）忽略伞绳对气动力的影响。

整个回收系统的回收方式为：引导伞+减速伞+大型翼伞。通过计算，稳定减速伞采用面积为790m2的圆形伞。在8 000m高空时，可将整个系统减速到35m/s左右，以此作为翼伞的计算输入条件。模拟迎角α=8°，–4°，0°，4°，8°，12°，14°，16°，18°，20°，22°，24°，26°，28°，32°。

在上述条件下，翼伞的气动性能受伞绳的影响不大，主要受翼型、切口等的影响；由于本次仿真针对的是稳定滑翔阶段的气动特性，伞衣基本不会再有变形，因此可以进行刚性假设，在此假设下，伞衣透气性的影响只能抛弃。但真实翼伞材料的透气量会对其升阻特性产生影响，这是由于透气量的增加会使其内腔泄压影响翼伞的刚性，同时其透过表面的气流会破坏边界层，促使分离。

1.3 网格建立

计算域为长200m、宽150m、高100m的长方体，基本满足无限远场的流场边界条件，流场内采用非结构网格进行填充。单元数约为2.5×106。翼伞模型网格如图4所示，为了准确捕捉流场信息，对距模型C处（见图5）的网格进行了加密，并在近壁区进行网格重构和细化以保证边界层计算条件。

图4 翼伞中间剖面网格Fig.4 Sectional grid of parafoil

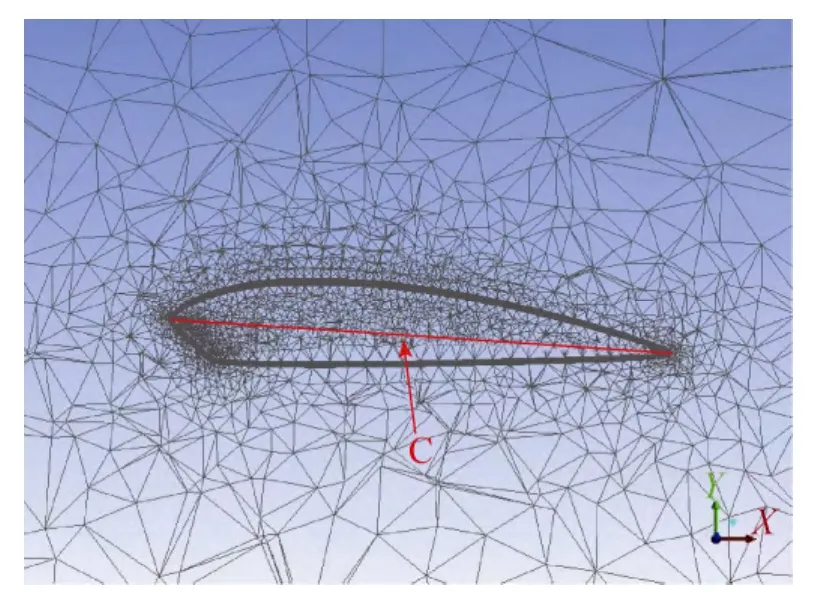
图5 近壁区剖面网格Fig.5 Sectional grid of the area near wall

2 充满状态下（伞衣鼓包）的翼伞气动性能

目前翼伞的气动试验数据大多是通过以下两种方式获得：一是刚性骨架的半柔性模型在风洞中吹风试验获得；一是通过专用支架强制改变全柔性翼伞的迎角，在风洞中吹风试验获得。因为本文主要是针对该回收系统的翼伞稳定滑翔阶段进行气动性能分析，并没有进行相应的风洞试验，所以只能对其整体曲线的趋势作出定性分析。

2.1 升阻特性

通过流场计算软件Fluent仿真得到的充满状态时，翼伞升阻力系数曲线，如图6所示，升阻比曲线如图7所示。

由图 6~7可知，充满状态的翼伞的升力系数随α的增大而增加，在α=18°处达到一个峰值，但在α=22°和α=26°左右有轻微波动，最后随α增大开始逐渐降低；翼伞的阻力系数在负迎角时，阻力系数随α增大而缓慢降低，而在正迎角时随α增大而增加；翼伞升阻比开始时随α增大而增加，在α=8°时达到最大值后，随α增大而逐渐降低。由于此次仿真缺少试验数据，这里只能与文献[1]里的试验数据作定性的对比分析。对比发现，本文仿真得出的翼伞阻力系数和升阻比曲线趋势与文献[1]中基本相符，而升力系数的趋势与文献[1]有一些差异，这种误差经分析可能是以下原因造成的：数值计算误差；本文采用的翼伞翼型与文献[1]中不同，且文献[1]中试验采用的翼伞为柔性模型，而在流场计算软件中只能假设其为刚体。

图6 翼伞升阻力系数曲线图Fig.6 The lift and drag coefficients graph of the parafoil

图7 翼伞升阻比曲线Fig.7 The lift-drag ratio graph of the parafoil

2.2 流场分布

为研究伞衣内的流场分布，取其升力最大的α=18°作为研究对象，图8给出了翼伞前缘切口速度矢量图。从图中可以看出，翼伞气室内流速很低，翼伞内部空气近乎滞止，形成高压区，同时伞衣前缘上表面与下表面产生小范围回流，这是由于来流受到前缘切口处压力梯度的影响。

图8 翼伞前缘切口速度矢量Fig.8 Velocity vector at the parafoil leading edge notch

图9给出了翼伞模型在α=0°，8°，16°时的中部剖面流场分布，可看出前缘切口附近压力梯度大且驻点压力分布较广，并沿切口呈清晰直线，气室内流速很低，压力基本均匀。对比图9中模型在α=0°，8°，16°时的流场图，可知当α较小时，前缘切口下表面压力梯度较大并随着α的增大而逐渐消失，这是由于α较小时腔内气流外翻，前缘分离，压强较低。随着α增大，前缘分离减弱，前缘压强增加，气流不再外翻，而直接流向下游。当α较大时，伞衣上表面前缘逐渐形成低压区，后缘产生分离并随α增加而逐渐加剧，产生脱体漩涡。

图9 不同α下，翼伞中部剖面的流场分布Fig.9 The flow distribution of the parafoil intermediate section with different α

3 单侧后缘下拉翼伞气动性能

翼伞后缘下拉过程类似于飞机机翼的副翼偏转，但它与副翼不同的地方在于当转弯和雀降过程中控制翼伞后缘下偏时，翼伞的后部将明显下折，而前部变形很小，表现出明显的柔性效应。同时，翼伞后缘下拉后，其升力和阻力都有所增加，同时产生转弯所需的力矩。翼伞转弯主要是通过操纵绳拉下一边后缘或关闭外翼一侧几个进气口使翼伞的单边外翼折倒来实现。本研究的回收系统设计中采用拉动操纵绳使一边后缘下偏来实现翼伞的转弯操纵，对比了单侧后缘下拉翼伞和普通翼伞的升阻特性，同时研究了其操纵性能。

3.1 单侧后缘下拉翼伞和普通翼伞的升阻特性比较

图10给出了单侧后缘下拉翼伞和普通翼伞的升力和阻力系数的比较曲线图，可以看出单侧后缘下拉使受力面积增加的同时提高了翼伞的升力和阻力系数。

图10 单侧后缘下拉翼伞和普通翼伞的升力和阻力系数的比较Fig.10 Comparison of lift and drag coefficient between unilateral flap deflection parafoil and ordinary parafoil

图11给出了单侧后缘下拉翼伞和普通翼伞的升阻比曲线，可以发现，单侧后缘下拉翼伞在α<0°时，升阻比比普通翼伞大，但α>0°时，升阻比比普通翼伞小，同时最大升阻比也比普通翼伞小，随着α的增加，在α=16°以后，二者的升阻比基本相同。

图11 单侧后缘下拉翼伞和普通翼伞的升阻比比较Fig.11 Comparison of lift-drag ratio between unilateral flap deflection parafoil and ordinary parafoil

3.2 单侧后缘下拉翼伞和普通翼伞力矩系数的比较

图12给出了普通翼伞力矩系数，可以看出在普通翼伞情况下，在α=14°前翼伞基本只有z方向力矩，即俯仰力矩；但α=14°后出现了小量的x方向力矩。由翼伞静稳定条件知，时，系统稳定，此处Cm为力矩系数。故在α<14°时，翼伞是基本稳定的。而在单侧后缘下拉情况下，下拉一侧的升力增加，对翼伞两侧形成升力差，并在横向平面内产生一定的滚转力矩；同时阻力的增加则在水平面内造成一个航向的偏转角速度。图13为单侧下拉翼伞力矩系数，图中可看出x方向力矩的增加使其滚转，同时翼伞y方向力矩的变化使其转弯，即翼伞的航向控制。一般来说，由于翼伞系统绕x和y的两种转动惯量相差较大，且回收物质量对滚转起阻碍作用，因此偏航比滚转更为明显。

图12 普通翼伞力矩系数Fig.12 The moment coefficient of the ordinary paraf

图13 单侧下拉翼伞力矩系数Fig.13 The moment coefficient of the unilateral

3.3 单侧后缘下拉翼伞和普通翼伞压力云图的比较

图14和15展示了α=14°时，普通翼伞和下拉翼伞的上下表面压力分布，从前缘到后缘，普通翼伞上表面压力逐渐增加，且前缘两侧压力较大而中间部位压力较小，后缘两侧压力较小，向中间部位压力先增大后减小。对比发现，普通翼伞对称平面两侧压力分布基本对称，下拉翼伞上表面表面压力分布与普通翼伞基本相似，但下表面处右侧下拉位置压力明显大于普通翼伞该位置的压力，可见单侧后缘下拉翼伞下拉处升力有所增加，从而翼伞两侧形成升力差，产生滚转力矩，进一步论证了上述力矩系数的比较结果。

图14 普通翼伞压力云图Fig.14 The pressure contour of the ordinary parafoil

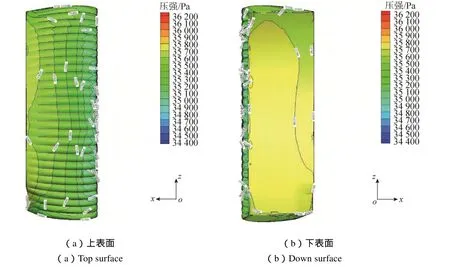
图15 下拉翼伞压力云图Fig.15 The pressure contour of the unilateral flap deflection parafoil

4 结束语

本文通过对考虑伞衣鼓包下翼伞模型的三维数值模拟，分析了翼伞在不同迎角α下的升阻特性和流场分布，比较了单侧后缘下拉翼伞和不下拉翼伞的气动性能，得出以下结论：

1）当α为负或较小的正值时，前缘切口下缘有较明显的压力梯度，并随着α的增大而逐渐消失，随着α的增大，伞衣上表面前缘逐渐形成低压区，后缘产生分离并随α增加而逐渐加剧。

2）翼伞的升力系数随α的增大而增加，在α=18°处达到一个峰值，但在α=22°和α=26°左右有轻微波动，最后随α增大开始逐渐降低。翼伞的阻力系数在负迎角时，阻力系数随α增大而缓慢降低，而在正迎角时随α增大而增加。翼伞升阻比开始时随α增大而增加，在α=8°时达到最大值后，随α增大而逐渐降低。

3）单侧后缘下拉翼伞相比普通翼伞升力与阻力系数均有所增加，但其最大升阻比却有所减小。

4）单侧后缘下拉后，升力增量使翼在横向平面内有一种侧滚的趋势，而阻力增量则在水平面内产生一个航向的力矩，因为翼伞系统绕x和y的两种转动惯量相差较大，且回收物质量对滚转起阻碍作用，因此偏航比滚转更为明显，从而实现了其航向控制。

随着回收物质量的增加和可控定点回收的要求，普通的圆形降落伞已经不能满足需求，只能选择有较高落点精度的可操控大型翼伞。本文为国内大型翼伞的研究工作提供了一定的参考。

References)

[1] 王利荣. 降落伞理论及应用[M]. 北京: 宇航出版社, 1997: 528-550. WANG Lirong. Parachute Theory and Application[M]. Beijing: China Astronautic Press, 1997: 528-550. (in Chinese)

[2] Nicolaides J D. Parafoil Wind Tunnel Tests[R]. AD731564, 1971.

[3] Thomas W B. Design, Development & Flight Testing of the NASA X-38 7, 500 FT2 Parafoil Recovery System [C]. AIAA 2003-2107, 2003.

[4] Madsen C M, Cerimele C J. Flight Perfromance, Aerodynamics, and Simulation Development for the X-38 Parafoil Test Program [C]. AIAA 2003-2108, 2003.

[5] 赵祖虎. 大型冲压翼伞空投试验[J]. 航天返回与遥感, 1995, 18(1): 4-12. ZHAO Zuhu. Air-drops Tests of a Large Parafoil[J]. Spacecraft Recovery & Remote Sensing,1995, 18(1): 4-12. (in Chinese)

[6] 贺卫亮. 利用风洞试验研究冲压翼伞的升阻特性[J]. 航空学报, 1999, 20(增), 75-77. HE Weiliang. Study on Lift-drag Characteristic of Ram Air Parafoil in Wind Tunnel[J]. Acta Aeronautica et Astronautica Sinica, 1999, 20(Suppl), 75-77. (in Chinese)

[7] Mittal S, Saxena P, Singh A. Computation of Two-dimensional Flows Past Ram-air Parachutes[J]. International Journal for Numerical Methods in Fluids, 2001, 35(6): 643-667.

[8] Balaji R, Mittal S, Rai A K. Effect of Leading Edge Cut on the Aerodynamics of Ram-air Parachutes[J]. International Journal for Numerical Methods in Fluids, 2005, 47(1): 1-17.

[9] Han Y H, Yang C X, Wang Y W, et al. Aerodynamics simulation of a large multi-cells parafoil[R]. AIAA-2009-2978, 2009.

[10] 李扬. 冲压式翼伞后缘下拉特性的数值研究[D]. 长沙: 国防科技大学, 2004. LI Yang. Numerical Simulation of Ram-air Parachute with Flap Deflection[D]. Changsha: National University of Defense Technology, 2004. (in Chinese)

[11] 李健. 前缘切口对冲压式翼伞的气动力影响[J]. 航天返回与遥感, 2005, 26(1): 36-41. LI Jian. The Aerodynamic Influence of the Cutter of the Front Edge of Parafoil[J]. Spacecraft Recovery & Remote Sensing, 2005, 26(1): 36-41. (in Chinese)

[12] 朱旭, 曹义华. 翼伞平面形状对翼伞气动性能的影响[J]. 航空学报, 2011, 32(11): 1998-2007. ZHU Xu, CAO Yihua. Numerical Simulation of Planform Geometry Effect on Parafoil Aerodynamic Performance[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(11): 1998-2007. (in Chinese)

[13] 朱旭, 曹义华. 翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响[J]. 航空学报, 2012, 33(7): 1189-1200. ZHU Xu, CAO Yihua. Effects of Arc-anhedral Angle, Airfoil and Leading Edge Cut on Parafoil Aerodynamic Performance[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1189-1200. (in Chinese)

[14] 张春, 曹义华. 基于弱耦合的翼伞气动变形数值模拟[J]. 北京航空航天大学学报, 2013, 39(5): 605-609. ZHANG Chun, CAO Yihua. Numerical Simulation of Parafoil Aerodynamics and Structural Deformation Based on Loose Coupled Method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(5): 605-609. (in Chinese)

[15] Altmann I H. Numerical Simulation of Parafoil Aerodynamics and Dynamic Behavior[C]. AIAA-2009-2947, 2009.