铁耗对感应电机矢量控制的影响及其优化控制

陈永超，高相铭，林成栋

(1.安阳师范学院物理与电气工程学院，河南安阳 455000;2.上海电机学院电气学院，上海 200240）

1 引言

随着电机驱动控制技术的发展，感应电机的矢量控制和直接转矩控制技术得到了广泛、深入的研究［1－2］，使感应电机的动态、稳态控制性能得到了大幅度的提高，甚至可以与直流电机的控制性能相媲美。就目前的研究而言，感应电机的控制策略大都建立在其传统的动态等效数学模型基础上，通常忽略感应电机铁耗和电机参数的变化［3－4］，造成理论上可获得高控制性能的控制策略在实际应用过程中无法获得令人满意的结果。随着参数辨识技术的不断发展，电机定、转子各项参数都可以得到准确实时辨识，有效的解决了电机参数变化对电机控制性能的影响［5］。这使得铁耗成为目前影响感应电机控制性能的最主要因素，特别在感应电机高速轻载运行时，采用忽略铁耗的电机模型对电机控制性能会造成较大的影响。文献［6－7］分析了感应电机矢量控制中，不考虑铁耗的矢量控制使得感应电机转子磁链幅值和转子磁场定向角的估算存在一定的偏差，导致磁链与转矩耦合，恶化了感应电机的矢量控制性能。为了得到更精确的控制，本文建立了在同步旋转d－q坐标系下考虑铁耗的感应电机动态等效数学模型，基于该模型分析了铁耗对感应电机控制性能的影响并推导得到了矢量控制的优化控制算法。通过基于RT－Lab半实物平台下的实验，验证了所提出优化算法的有效性。

2 考虑铁耗的感应电机数学模型

感应电机的铁耗可以分为定子铁耗和转子铁耗，是同步旋转磁场分别切割定、转子使定、转子铁芯中磁通交变从而产生的磁滞损耗和涡流损耗之和［8］。其中磁滞损耗与磁场交变频率成正比，涡流损耗与磁场交变频率的平方成正比。当电机正常高速运行时，定子铁芯中磁场交变频率远高于转子铁芯中磁场交变频率，因此定子铁芯中的涡流损耗是铁耗的主要成因。

感应电机的铁耗由主磁通密度决定，即与激磁电流有关，而与感应电机的负荷大小基本无关，因此可在决定激磁电流的电动势两端并联一个电阻Rm用于等效感应电机的铁耗［9］，并可根据坐标变换得到同步旋转d－q坐标系下考虑铁耗的感应电机等效电路，如图1所示。

图中Rs、ls分别为定子电阻、定子漏感;Rr、lr分别为转子电阻、转子漏感;φrd、φrq分别为两相旋转坐标系下d、q轴转子磁链;Lm为激磁电感;w1为同步速度;wr为转子转速;Rm为等效铁耗电阻;usd、usq分别为 d、q 轴定子电压;isd、isq分别为 d、q轴定子电流;ird、irq分别为d、q轴转子电流;ifed、ifeq分别为d、q轴流过等效铁耗电阻的电流;imd、imq分别为d、q轴的激磁电流。

图1对应的电压方程为:

式中np为磁极对数，Lr为转子自感。

3 铁耗对感应电机矢量控制的影响

感应电机的矢量控制是基于转子磁场定向的控制，其关键是获得准确的转子磁链位置，将定子电流解耦为转矩分量和激磁分量，从而获得较高的控制性能［10］。

感应电机在负载运行时，定子磁动势F1可分成两部分:产生气隙主磁场Bm的激磁磁动势Fm和抵消转子磁动势的负载分量 －F2，如图2所示。对应地，定子绕组电流I1也可分成激磁电流Im和转子负载电流－I2两部分。当计及铁芯损耗时，Bm在空间滞后于Fm以铁耗角 αFe［11］。如果不考虑铁耗，则图2中不存在铁耗角，激磁电流和气隙主磁通的矢量在同一方向，激磁电流中不存在有功分量。

当考虑铁耗时，在感应电机动态等效电路中增加了铁耗等效电阻Rm，其中流过的电流ife是铁耗等效电阻从定子电流中分得的。这说明考虑铁耗后，感应电机的定子电流将有所增加，必须从电源侧吸取更多的有功功率来弥补铁芯中的损耗。

传统的感应电机矢量控制器都是在忽略铁耗的前提下设计的，而用不带铁耗补偿的矢量控制器控制感应电机时，即使在电机参数辨识准确的情况下，实际的转子磁链也会受铁耗的影响，与矢量控制器计算出的转子磁链存在偏差，使得转子磁场定向不准确。当磁场定向角存在偏差时，会使得d、q轴各分量相互耦合，无法完全解耦。

传统矢量控制中磁场定向的偏差如图3所示，假设电机中实际的转子磁场所在位置d轴，而采用忽略铁耗的等效电路对转子磁场的定向会有所误差，转子磁场估算位置在d’轴，偏差角度为θ。只要电机在正常运行就必然存在铁耗，所以传统磁场定向必然存在角度偏差。在一定负载下，随着速度的上升铁芯中磁通交变频率增大，必然带来铁耗的增加，所以会导致偏差角度增大。当电机速度一定时，随着负载的增加，铁耗在有功功率中所占比重逐渐减小，磁场定向角度偏差就越小，磁场定向越精确。

由于转子磁场定向的误差一定存在，这会对d、q轴电流都有影响，所以无法分解得到最优的isd和isq。在闭环控制系统中，这将导致反馈的励磁电流和转矩电流分量与实际值不一致，从而对电机的动静态性能产生一定影响。

根据式(7）可知，考虑铁耗时的感应电机的实际输出转矩要小于不考虑铁耗时的转矩计算值。所以在传统的矢量控制中，由于铁耗的存在会消耗一部分电磁转矩，从而使感应电机实际获得的电磁转矩比计算值偏小，这种铁耗的阻尼作用使得传统矢量控制的控制性能变差，降低了电机动态响应性能。

4 矢量控制的铁耗补偿优化

从式(13）中可以看出，与传统的矢量控制不同，磁链分量与转矩分量同时受到了转子电流ird、irq的影响，激磁与转矩分量不再解耦。传统的矢量控制方法忽略了铁耗等效电阻在这方面的影响，磁场定向与输出转矩的控制都是不准确的。当Rm趋向无穷大的时候，即忽略铁耗的影响，由(13）可得:

可以看出，式(14）与传统矢量控制完全一致。但是当铁耗较大，即铁耗等效电阻较小的时候，忽略Rm便会产生较大的定向误差。

为了简化控制算法，去掉式(12）中的微分项，就能够在稳态条件下实现精确磁场定位控制，得到简化的控制方案如下:

考虑铁耗的矢量控制可参考传统的磁链开环转差频率矢量控制系统。其基本控制思路是保持转子的激磁电流分量不变，通过改变转矩电流分量来改变转差频率，从而改变感应电动机的电磁转矩［12］。

为了避免传统矢量控制中由于忽略铁耗而造成转子磁场定向存在偏差，可利用式(15）对传统的磁链开环转差频率型矢量控制系统进行优化。考虑铁耗的矢量控制系统框图如图4所示。与传统的转差频率矢量控制相比，只是在电流指令值计算环节增加了考虑铁耗后的优化控制部分。因此从控制方案实现的角度考虑，并不需要做太多修改就可实现考虑铁耗的矢量控制。由式(15）可以看出，同步转速越高，进行优化控制需要补偿的电流分量也越大。因此，铁耗补偿在电机高速轻载时运行时应该具有更明显的优化效果。该优化控制方案能够实现稳态下考虑铁耗的精确转子磁场定向，从而提高系统控制性能。

另外，在转速磁通双闭环的控制系统中，在对转子磁通进行观测时，为了更加准且的体现磁通的动态相应过程，不同于传统矢量控制中转子磁通幅值直接由isd获得的方法，可以利用相电流采样并进行park变换获得isd和isq后，通过反解式(15）计算出imd，从而进一步计算得到ψr。

4 实验验证

为验证考虑铁耗矢量控制优化算法的有效性，对其进行实验研究。实验采用以RT－Lab为核心的半实物仿真平台，仿真中除考虑铁耗的矢量控制算法通过RT－Lab仿真器实现外，电机、逆变器、采样电路等均通过实物实现。异步电动机参数如表1所示。

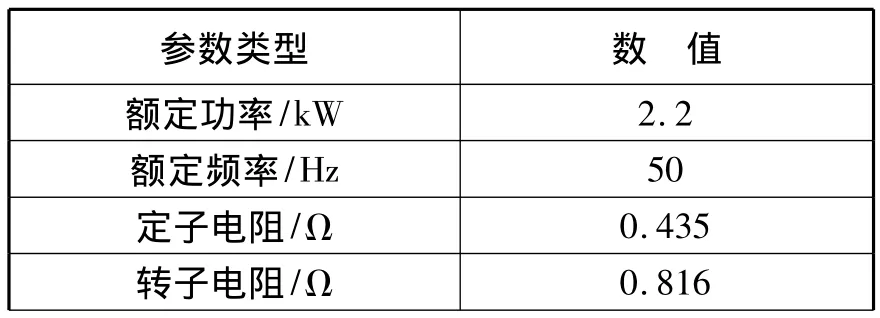
表1 感应电动机参数Tab.1 Parameters of IM

参数类型 数 值定子自感/H 0.071转子自感/H 0.071激磁电感/H 0.069额定等效铁耗电阻/Ω 7极对数2转动惯量/(kg·m2）0.19

通过在上位机中利用Matlab/Simulink和RT－Lab软件，完成建模、在线调参及信号监控等工作。另外用一台Opal RT公司专为半实物仿真应用而设计的基于PC的实时仿真器作为目标机。目标机内部配置有四核处理器，运行QNX实时操作系统。由目标机完成模型的分布式实时计算、定子电流和相电压的采样、生成逆变器所需的PWM信号等工作。PWM信号利用Rt－Events工具箱中的RTE－PWM模块产生，然后由数字板卡OP5252输出。

通过速度阶跃响应实验来检测补偿效果，电机在空载条件下起动，转速指令值为1400r/min。在0.4s时，给定速度指令阶跃到1000r/min。应用铁耗优化控制前后，电机转速响应的波形如图5所示。从图中可以看出，经过铁耗补偿之后，速度响应性能有所改善，说明铁耗优化补偿有助于矢量控制性能提高。

实验中给定转子磁链值为0.7，电机稳态工作时A相定子电流如图6所示。定子电流采样后经park变换，由式(15）解出imd，然后由式(9）计算获得转子磁链波形如图7所示。从图中可以看出转子磁链在指令值附近上下较小范围内波动，证明考虑铁耗的矢量控制优化补偿算法能够准确跟踪转子磁链指令值，反映出其对磁场有较好的定向能力。

5 结论

本文建立了考虑铁耗的异步电动机等效动态数学模型，分析了传统矢量控制中异步电动机铁耗带来的影响。为了避免由铁耗导致转子磁场定向不准确和电磁转矩降低从而使电机的控制性能下降，本文根据考虑铁耗的电机等效动态数学模型，推导得到了考虑铁耗的优化补偿算法，该算法简单，便于工程实现。实验结果表明进行铁耗优化补偿后，电机的动态、稳态响应性能有所改善，验证了所提算法的有效性。

［1］崔纳新，张承慧.变频调速异步电动机效率优化控制的研究进展［J］.电工技术学报，2004，19(5）:36 －42.

［2］聂子玲，马伟明，李卫超.矢量控制感应电动机H∞磁通观测器研究［J］.电工技术学报，2006，21(8）:31－35.

［3］赵争鸣，袁立强，孟朔 等.通用变频器矢量控制与直接转矩控制特性比较［J］.电工技术学报，2004，19(4）:81－84.

［4］张云，孙力，吴凤江 等.考虑铁耗的异步电动机模型及对矢量控制的影响［J］.电机与控制学报，2007，11(4）:359－363.

［5］张虎，李正熙，童朝南.基于递推最小二乘算法的感应电动机参数离线辨识［J］.中国电机工程学报，2011，31(18）:79 －86.

［6］张云，孙力，吴凤江 等.考虑铁耗的感应电机模型及对矢量控制的影响［J］.电机与控制学报，2007，11(4）:359－363.

［7］Choi J W，Chung D W，Sul S K.Implementation of field oriented induction machine considering iron loss［C］.11th Annual Applied Power Electronics Conference and Exposition，1996:375 －379.

［8］罗应立，赵海森，姚丙雷 等.交流电机铁耗的工程计算方法分析［J］.电机与控制应用，2010，(11）.

［9］李洁，钟彦儒.考虑铁损的感应电动机仿真模型研究［J］.系统仿真学报，2005，17(10）:330－337.

［10］李永东.交流电机数字控制系统［M］.北京:机械工业出版社，2002.88 －96.

［11］汤蕴璆，罗应力，梁艳萍.电机学［M］.北京:机械工业出版社，2009.162－168.

［12］阮毅，陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社，2012.188－189.