“平行四边形的面积”教学实录与评析
朱俊龙 梁万美
教学内容:人教版数学五年级上册第六单元第一课时。
教学过程:
一、情境导入,快速切题
师:请同学们观察我手中的两张白纸,你发现了什么?
生1:形状不相同,一张是长方形,另一张是平行四边形。
生2:上面都画有小方格。
师:同学们观察得很仔细,谁能猜猜这两张白纸哪一张要大一点呢?
生1:长方形这张白纸要大一点。(多数同意)
生2:平行四边形这张白纸要大一点。(少数同意)
师:用什么方法来证明你们的猜想呢?
生:计算出两张白纸的面积。
师:同学们真聪明!下面,我们就来学习平行四边形面积的计算方法。(板书课题:平行四边形的面积)
评析:教师利用两张简单的白纸迅速把学生引入学习的主题,做到了精讲,突出了教师主导、学生主体的地位。
二、继续学习,探讨方法。
师:谁知道长方形的面积是多少呢?(提示:白纸上的每个小方格的面积是1平方厘米。)
生1:数小方格,长方形上面有18个小方格,它的面积是18平方厘米。
生2:用6乘3等18,它的面积就是18平方厘米。
生3:用公式,长方形的面积等于长乘宽。
(此时教师顺势请这位学生板书长方形的面积计算公式。长方形的面积=长×宽)
师:同学们真棒,这么快就算出了长方形的面积,并且找到这么多的计算方法。谁数出了平行四边形上面的小方格,它的面积是多少呢?(没人回答)
师:同学们有困难吗?(提示:不满1格的都按半格计算。)
生:平行四边形的面积数得18平方厘米。
师:同学们,今后我们要计算平行四边形的面积,用数方格的方法方便吗?
生:不方便。
师:是呀!下面我们就继续学习用其他的方法来计算平行四边形的面积。老师用这把剪刀把这个平行四边形进行整容,谁来说说如何整容呢?
生1:沿着方格虚线条把平行四边形的左边的直角三角形剪掉,拼在右边,把它拼成长方形。
生2:沿着方格虚线条把左边剪下的直角梯形和右边的直角梯形拼在一起,也能得到一个长方形。
师:我就先按照第一位同学的想法剪剪,看这个平行四边形被整容后会变成什么?
师:老师剪好了,谁上来拼一拼?
(生1上台拼出了一个长方形。)
师:我又按照第二位同学们的想法剪剪,看这个平行四边形被整容后会变成什么?
师:老师剪好了,谁再上来拼一拼?
(生2也拼出了一个长方形。)
(教师边示范边简述平行四边形转化成长方形的过程。)
师:现在能计算出平行四边形的面积了吗?
(生很快说出平行四边形的面积是18平方厘米。)
师:谁说说这种整容方法叫什么?(师提示:割这边补上那边。)
生:割补法。
师:回答得真棒!以后如果要计算平行四边形的面积都采用这样的割补法,方便吗?
生:不方便。
师:谁能根据这种割补出来的图形总结出平行四边形面积的计算方法呢?
生:根据长方形的面积计算方法来算,平行四边形的面积=长×宽。
师:那么长和宽怎样知道呢?(提示:同学们请注意了,平行四边形割补后的小方格,从横向看一层有几个方格?从纵向看(竖直)有几层小方格?)
生1:横着有6个小方格,竖着有3个小方格。
生2:把横向的6个小方格看成长,把纵向的3个小方格看成宽。
师:拼成长方形的“长”和“宽”,在平行四边形里分别叫什么名称呢?
生1:长方形的“长”就是平行四边形的“底”。
生2:长方形的“宽”就是平行四边形的“高”。
师:同学们真聪明!谁来再次总结一下平行四边形的面积计算方法?
生:平行四边形的面积=底×高。(师板书)
长方形的面积=长×宽
↓ ↓ ↓
平行四边的面积=底×高
评析:教师通过直观实物教具,进行实践操作,引导学生进行实际拼补,在实践中探究,在探究中学习。使学生根据长方形面积的计算方法来探讨平行四边形面积的计算方法,在实践和探究中让学生自主生成新知识,教学方法灵活。在教学中,教师遵循由浅入深,由简到繁,由具体到抽象的认知规律,合理运用知识的迁移,总结出平行四边形的面积计算公式,使学生很快找到了解决问题的办法,让学生在学习中找到了快乐,尝到了成功的喜悦。
三、学习课例,深入理解
(师课件出示教材第87页情境图)
为了创建文明城市,美化我们的生活环境,某社区准备修建两个大花坛。这两个花坛分别是什么形状的?(一个长方形,一个平行四边形。)
师:同学们猜猜,你觉得哪一个花坛大一些?
生:要想比较哪个花坛大,需要计算它们的面积。
师:用展示台出示长方形的方格图和平行四边形的方格图。问:如果每个小方格代表1平方厘米,这个长方形的面积是多少?平行四边形的面积是多少?
生1:通过数方格和用公式计算,长方形面积是24平方厘米。
生2:通过数方格和用公式计算,平行四边形的面积也是24平方厘米。
师:同学们怎样找到长和宽,底和高呢?
生1:长方形中,长有几个小方格就是几厘米,宽有几个小方格就是几厘米。
生2:平行四边形中,底边有几个小方格,那么底就是几厘米,高有几个小方格,高就是几厘米。
师:谁能用字母把这两种图形的面积公式写出来?
生1:(长方形的面积)s=(长)a×(宽)b。
生2:(平行四边形的面积)s=(底)a×(高)h。
师:请同学们继续看方格图,填第87页下方的表,填完后再认真观察,发现了什么?讨论一下,总结出规律。
生:我发现长方形的长和宽与平行四边形的底和高分别相同,它们的面积也就相同。
师小结:是呀!如果长方形的长和宽分别等于平行四边形的底和高,则它们的面积相等。
评析:教师利用先前学到的新知识来解决课例中的问题,有利于强化学生对新知识的巩固,并逐步加深对知识的应用,在观察、训练和思考中寻找隐藏的规律,做到了研究教材、利用教材和挖掘教材。把握了教学重点,突破了教学难点,渗透了数学来源于生活并服务于生活的思想。
四、练习提高,巩固新知
1.一块平行四边形的麦地底长350米,高是80米,它的面积是多少平方米?
师:同学们各自解答,集体订正。
师:如果把问题改为:“每公顷地可收小麦7000千克,这块地共可收小麦多少千克?”必须要知道哪些条件?
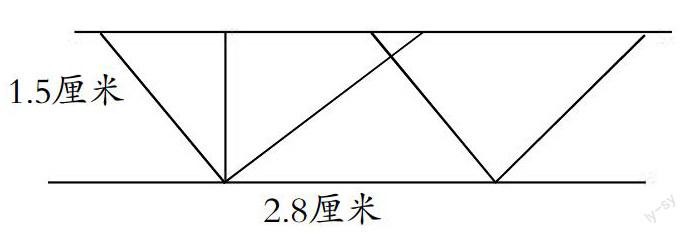
2、练习十九第6题:
师:你能找出图中的两个平行四边形吗?他们的面积相等吗?为什么?你可以得出什么结论呢?(等底等高的平行四边形的面积相等。)
评析:教师通过一题多变引导学生习得知识,从不同的角度去解决实际问题,达到了横向学习,纵深发展的效果。使学生学到的知识更系统化、具体化,运用自如。在老师的启发下,在探究、交流中获得知识,增强了学生的成就感,培养了学生的学习兴趣。

