杏仁牛奶巧克力的品质变化动力学模型及货架期预测
文 / 朱扬玲(通标标准技术服务(上海)有限公司 上海201506)
杏仁牛奶巧克力的品质变化动力学模型及货架期预测
文 / 朱扬玲(通标标准技术服务(上海)有限公司 上海201506)
为研究杏仁牛奶巧克力的货架期预测方法,设定了15℃、25℃、20℃3各不同储藏温度,并对感官、水分、菌落总数、酸价进行了检测。本研究采用Arrheniu 方程对品质变化速率常数和温度T进行线性拟合,得到的活化能Ea为16.94KJ/mol,预测获得的货架期(20℃)为589天,按照安全系数0.8计算,保质期为15个月。实验证明,Arrhenius一级动力学模型能较好地描述15~30℃储藏条件下的杏仁牛奶巧克力的品质变化,预测方程的拟合程度较高,决定系数R2为0.9942,预测结果参考价值较大。
1、引言
货架期(shelf life),又称货架寿命,或保质期等。食品货架期一般受内部因素(包括微生物数量、酶促反应和生化反应等)、外部因素(包括温度、相对湿度、pH值、压力、辐射等)及包装材料等影响[1]。一般情况下,食品保质期是根据食品品质变得难以接受的天数,乘以0.7-0.8的安全系数来计算的。由于现代食品工业的发展,许多预包装食品的货架期可以超过1年。因此,对食品行业来说,在一个较短的时间内确定产品的货架寿命是很有必要的。
随着交叉学科的相互渗透,各种动力学模型在食品货架期预测中应用越来越广泛,包括阿伦尼乌斯(Arrhenius)方程[2]、威布尔危险值分析方法(Weibull Hazard Analysis, WHA)[3,4]、WLF(Williams-Landel-Ferry)方程[5]、Z值模型法[6,7]等。其中,动力学模型结合Arrhenius方程是最经典,也是应用最广泛的一种货架期预测方法。2003年,Suh等[8]通过建立0级反应动力学模型,研究了温度对桑葚汁褪色的影响,并通过统计分析确定了4个不同pH值的样品,在80℃-100℃间的活化能。谢晶等[9]采用Arrhenius方程对品质变化速率常数k和温度T进行非线性拟合,得到还原型抗坏血酸、叶绿素、L*(亮度)和ΔE活化能Ea分别为68.130、57.024、46.685 和42.581 kJ/mol。最终得到以时间、温度和品质指标值为变量的上海青货架期预测方程,拟定不同的品质终点值能得到对应的货架期。本文利用Arrhenius方程,以酸价为主要质量指标对杏仁牛奶巧克力的货架期进行预测,为动力学模型在食品货架期预测中的应用提供科学依据。
2 、材料和方法
2.1 材料、试剂
本实验采用新鲜生产的杏仁牛奶巧克力,包装后立即放置在不同温度条件下进行储藏。氯仿、冰醋酸、碘化钾等为分析纯试剂;淀粉指示剂。
2.2 仪器
LHS-250HC-I恒温恒湿箱、CNFDC-40生化培养箱、CNFDM-53电热恒温鼓风干燥箱、CNFDM-246紫外可见分光光度计等。
2.3 实验设计
2.3.1 储藏条件
本实验设置了3个储藏温度,分别为15℃、25℃、30℃。
2.3.2 质量指标
脂肪的氧化酸败是导致本样品变质的主要因素,本实验以酸价≥2.0mg/g作为货架期终点。同时对产品中的感官、菌落总数、水分含量、酸价进行检测,作为判断货架期终点的辅助指标。
2.3.3 测试间隔时间与储藏时间
测试间隔时间为25天,储藏125天。
3、结果与分析
3.1 储藏时间内质量指标的变化
对储藏在15℃、25℃、30℃下的样品,每25天检测一次。表1是储藏时间内辅助质量指标的变化,图1是储藏时间内主要质量指标酸价随时间的变化。从表1可以看出,在储藏期间内,感官、菌落总数、水分含量等质量指标比较稳定,变化较小。微生物生长和水分流失的速度较慢,不会影响产品的品质。而从图1可以看出,酸价在储藏期间内呈明显上升的趋势,15℃、25℃、30℃温度下,酸价从初始值0.88mg/g,分别上升到了1.08mg/g、1.15mg/g和1.19mg/g,变化较大,证明了油脂氧化酸败是样品变质的主要因素。
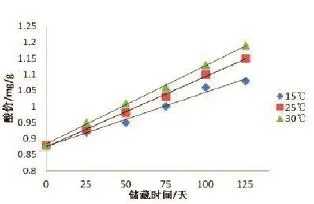
图1 不同储藏温度下酸价随时间的变化
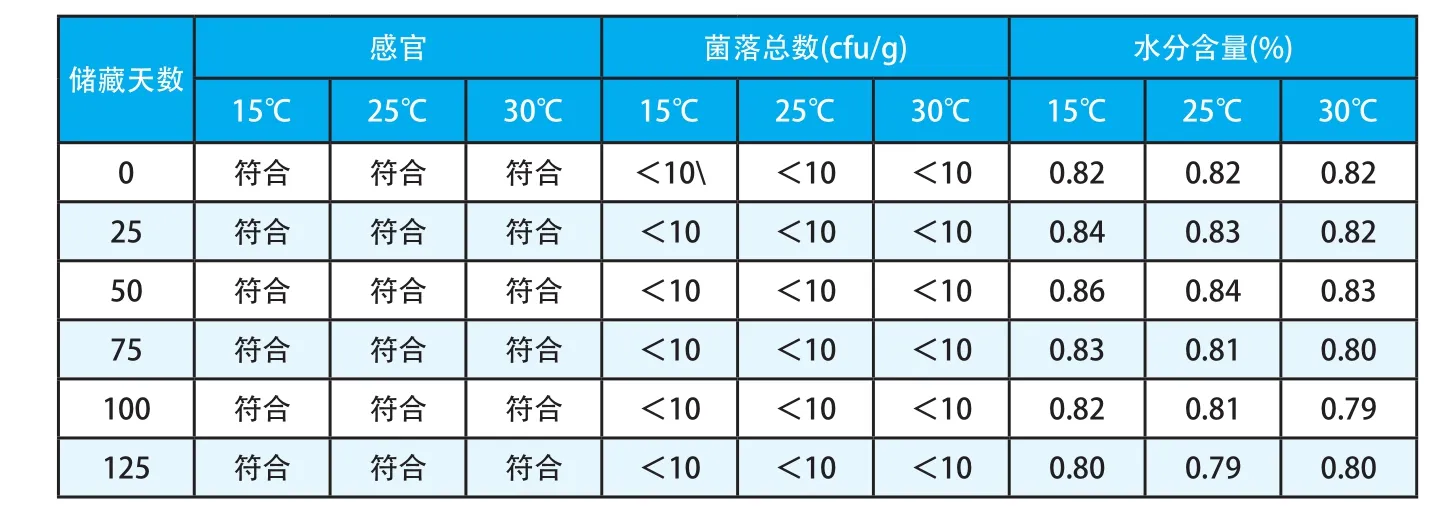
表1 不同储藏温度下辅助质量指标的变化
3.2 动力学分析及货架期预测
在大多数情况下,温度是影响食品货架期的主要因素,而且是唯一不受食品包装类型影响的因素[10]。Arrhenius方程是物理化学中研究温度与反应速度常数关系的,反映了温度与食品腐败变质速率的关系[11]。Arrhenius动力学方程如表2所示。

表2 不同反应级数的动力学方程
式中:A0为指前因子,也叫频率因子,也相当于活化能为零时的反应速率;Ea为活化能,品质因子变坏或形成需要克服的能耗;T为绝对温度,K;R为气体常数1.9872cal/ (mol・K)或8.3144 J/(mol・K)。其中,A0和Ea都是与反应系统物质本性有关的经验常数。
由某种化学反应或微生物生长引起的品质变化,用该品质变化表示的货架寿命大多属于零级(如冷冻食品的整体品质、美拉德反应)或一级(如维生素损失,氧化引起的褪色,微生物生长与失活)[11,12]。对于零级模式,在线性坐标上可得一条直线;对于一级模式,采用半对数坐标系可得一条直线;对于二级模式,1/A对时间作图可得一条直线。根据少数几个测定值和线性拟合的方法就可求得上述级数,并可求出k值(斜率),然后通过外推求出货架寿命终端时的品质值,也可计算出品质达到一特定值时的贮藏时间,当然也可以计算出任一贮藏时间时的品质值[13]。
3.2.1 动力学分析对图1中数据进行线性回归分析,得到不同温度下的变质速率常数及决定系数,如表3所示。一级动力学回归的决定系数R2均>0.98,说明线性拟合较好,不同温度下的酸价变化,符合一级动力学模型。
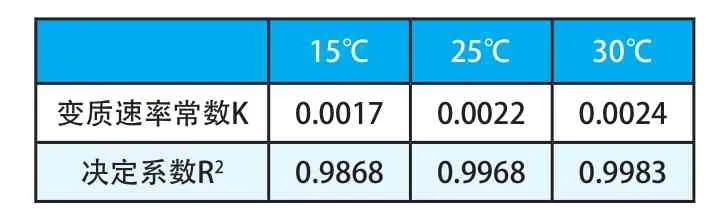
表3 一级反应动力学回归速率常数K和决定系数R2
3.2.2 货架期预测
获得表3中不同温度下的变质速率常数K后,通过对lnK和1/T进行线性拟合,得到一条斜率为-Ea/R,常数项为lnA0的直线,即杏仁牛奶巧克力变质速率与温度的关系:

从方程中可知,直线的斜率-Ea/R为-2037.7,lnA0为0.7033,从而可计算出活化能Ea为16.94KJ/mol,如表4所示。通过这个方程,利用用外推法即可获得正常储藏温度(18℃)下的货架期,为589天。
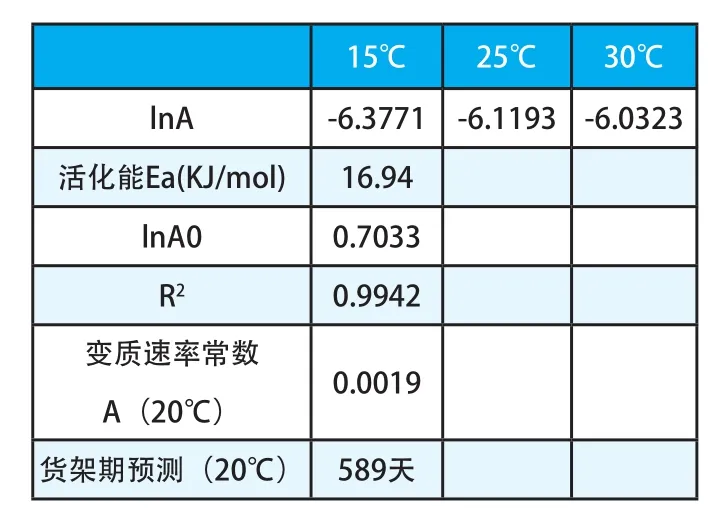
表4 20℃条件下的货架期预测
4、结论
结果表明,Arrhenius一级动力学方程能较好地描述15~30℃储藏条件下的杏仁牛奶巧克力的品质变化,结合动力学分析方程可以预测杏仁牛奶巧克力的货架期。最终得到以储藏温度和储藏时间为变量的货架期预测方程,决定系数R2为0.9942,拟合程度较高。通过这个方程,计算出正常储藏温度(18℃)下的货架期为589天,按照安全系数0.8计算,其保质期为15个月。
综上所述,经典的Arrhenius动力学模型在杏仁巧克力的货架期预测中得到了较好的应用,大大缩短了保质期研究的周期,并为今后在其他食品货架期研究中的应用提供科学依据。
5 、讨论
随着食品货架期研究的深入,Arrhenius模型在食品货架期预测中的应用也越来越广泛。Arrhenius动力学,为食品货架期加速试验(ASLT)的设计提供了理论基础,使研究者们可以在较高的储藏条件下采集数据,然后用外推法求得较低温度下的货架期,大大缩短了测试周期[14,15]。但Arrhenius模型也有其局限性。
5.1 温度范围的局限性
Arrhenius方程虽然反映了食品的腐败变质速率与温度的关系,但只在一定温度范围内适用[16]。在本研究中,由于巧克力的熔点为35℃,因此,为了确保巧克力在加速试验(破坏试验)中保持正常的外观形态,最高温度设为30℃,导致测试周期较长。但是在其他食品的应用中,可将加速条件的温度设置的高一些,但仍需确保在外观上与正常状态一致。最重要的是,加速试验的保藏温度,不能改变食品的主要变质因素。如脱水马铃薯,在温度超过30~32℃时,主要变质因素是非酶促褐变,而在温度低于30~32℃时,主要变质因素为脂类氧化。因此,两个温度范围内的动力学方程也不同。
5.2 储藏温度及储藏时间的确定
研究表明,在做加速实验(破坏试验)时,食品的腐败变质程度达到50%~70%,预测的准确度才比较高[17]。在加速温度较低时,储藏周期也会比较长。由于巧克力的融化温度在35℃左右,因此加速试验的最高储藏温度设置为30℃。本实验中,酸价的临界值为2.0mg/g,超过临界值的产品判定为不可食用。因此,货架期试验的终点,酸价必须大于1.0mg/g。
5.3 置信区间
应用回归分析方法来计算Arrhenius方程的参数值时,可用统计分析的方法来确定置信度达到95%的Arrhenius参数值。但是只有3个温度下的变质速率常数k,其置信范围往往很宽,因此,要获得置信度范围足够窄的Ea和K,则必须多设计几组温度条件[18]。
[1] 曹悦,陆利霞,熊晓辉.食品货架期预测新技术进展[J]。食品研究与开发,2009,30(5):165-168
[2] Mossel B, Bhandari B, D’ Arcy B, et al, Use of an Arrhenius Model to predict rheological behavior in some Australian honeys [J], Leben smittel-Wissenschaft and technologie, 2003, 36(1):49-65
[3] Cardelli C, Labuza T.P. Application of weibull hazard analysis to the determination of the shelf life of masted and ground coffe [J], Lebensm Wissu Techno, 2001, 34(3):273-278
[4] E. Al-Kadamany, I. Toufeili, M.Khattar etc. Determination of Shelf Life of Concentrated Yogurt (Labneh) Produced by In-Bag Straaining of Set Yogurt using Hazard Analysis [J]. J. Dairy Sci, 2002(85):1023-1030
[5] Hagiwara T, Hartel R W. Effect of sweetener, stabilizer, and storage temperature on ice recrystallization in ice cream [J]. Journal of Dairy Science, 1996, 79:735-744
[6] Fujikawa. H, Itoh, T. Thermal inactivation analysis of Mesophiles using the Arrhenius model and Z-value models [J]. J.Food. Prot, 1998, 61(7):910-912
[7] Jonsson V, Sngag B.G. Testing models for temperature dependence of the inactivation rate of bacillus spors [J]. J. Food. Sci, 1997, 42(5):1251-1252
[8] Suh HJ, Noh DO, Kang CS et al. Thermal kinetics of color degradation of mulberry fruit extract [J]. Nahrung, 2003,47:132-135
[9] 谢晶,张利平等.上海青蔬菜的品质变化动力学模型及货架期预测[J].农业工程学报,2013,29(15):271-278.
[10] Mimi Sherlock, Theodore P. Labuza, Consumer Perception of Consumer Time-Temperature indicators for Use on Refrigerated Dairy Foods [J]. Journal of Dairy Science, 1992, 75(11):3167-3176
[11] Maria G., Corradini, Micha Peleg. Shelf life estimation from accelerate storage data [J]. Trends in Foof Science and Technology, 2007(18):37-47
[12] Martinus A.J.S van Boekel. Kinetic Modeling of Food Quality: A Critical Review [J]. Comprehensive reviews in food science and food safety, 2008(7):144-158
[13] Martins R C, Lopes I C, Silva C L M . Accelerated life testing of frozen green beans (Phaseolus vulgaris, L.) quality loss kinetics: colour and starch[J]. Journal of Food Engineering , 2005,67 (3): 339-346.
[14] An J S, Zhang M, Lu Q R, et al, Effect of a prestorage treatment with 6-benzylaminopurine and modified atmosphere packaging storage on the respiration and quality of green asparagus spears. Journal of Food Engineering[J].2006, 77(4):951-957
[15] Michael E N A, David S. Robinson. Food shelf lifestability: chemical, biochemical, and microbiological changes[M]. Boca Raton: CRC Press.2001:38-41

[16] Oliveira F A R, Sousa-Gallagher M J, Mahajan P V, et al. Development of shelflife kinetic model for modified atmosphere packaging of fresh sliced mushrooms[J]. Journal of Food Engineering, 2012,111 (2): 466-473.
[17] 高大元,何碧,何松伟等.Arrhenius方法的局限性讨论[J].含能材料,2006,12(2):132-135
[18] 任亚妮,车振明等.应用ASLT法预测软面包的货架期[J].食品研究与开发,2011,32(2):156-158
Quality kinetic model and shelf life prediction of
almond milk chocolate
Zhu Yangling
(SGS-CSTC Standards Technical Services Co. Ltd, Shanghai201506, China)
Summary: With the widely utilization of quality kinetic model in the field of shelf life prediction, the Arrhenius model was conducted through a series experiments and validation. The parameters such as sensory evaluation, moisture content, total plant count and acid value were determined in this experiment, then a kinetic analysis of those quality indexes was studied. The result showed that the quality determined change was adequately described by first-order reaction kinetics. The liear fitting of reacton rate K and temperature T based on Arrhenius law was also studied, from which active energy Ea was 16.94 KJ/ mol, and the shelf life predicted was 589 days (R2>0.99). This conclution is expected to offer a theoretical basis for shelf life prediction of food.

