一种新的混合矢量磁滞模型磁滞算子定义方法

李丹丹 刘福贵 李永建 赵志刚 杨庆新,

（1.河北工业大学河北省电磁场与电器可靠性省部共建重点实验室 天津 300130 2.天津工业大学天津市电工电能新技术重点实验室 天津 300387）

1 引言

对铁心材料磁特性进行精确建模是提高电机工作性能和运行效率并降低能耗的重要途径，也是国际电工领域的前沿和热点问题，但由于问题本身的复杂性，这一领域一直处于发展阶段。到目前为止，各国学者已经提出了多种模型用来模拟材料的磁滞现象，主要提出了两类磁滞模型，一类是纯数学模型（例如Preisach 模型[1]和Hodgdon 模型[2]），另一类是物理模型（例如Stoner-Wohlfarth（S-W）模型[3]和Jiles-Atherton（J-A）模型[4]）。由于电磁装置运行中磁心特性多呈矢量磁特性，而经典基础模型大都是标量模型，不能精确模拟磁材料在工程应用中的磁特性，为此学者们使用各种方法把经典标量模型扩展到矢量范畴，如Mayergoyz 模型[5]和Coupled Hysterons 模型[6]等。经典S-W 模型适用于椭球形、单畴、单轴磁性粒子矢量磁特性模拟，在这些限定条件下可描述多种磁特性。Mayergoyz 模型用各个方向上磁化强度的连续分量的矢量和计算总磁化强度，该模型比S-W 模型更具普遍性，但不能精确模拟旋转外加场下的磁特性。Coupled Hysterons 模型对于具有椭球形粒子的磁材料能准确描述其饱和特性和损耗特性，但在建模时需要根据磁化过程进行旋转和定位修正。

近十几年结合两种或多种经典模型的混合磁滞模型逐渐成为磁滞模型的发展趋势。从20 世纪90 年代开始，学者们就试图用标量Preisach 模型与矢量S-W 模型相结合的方法对材料磁特性进行模拟[7,8]。2006 年Della Torre 等人提出了一般矢量磁滞模型（后被称为DPC 模型）[9,10]，后续又提出了Preisach-Stoner- Wohlfarth（PSW）模型[11]，混合磁滞模型的发展步入系统化阶段。PSW 模型使用外加磁场与粒子间的相互影响场的矢量和定义了一个网络场，利用网络场确定磁化方向和磁化强度幅值[12-15]；而DPC 模型的磁化方向和磁化强度幅值是分别由S-W 模型和Preisach 模型确定的[16-20]。这两种模型都是通过结合Preisach 模型和S-W 模型进行建模的，统称为混合矢量磁滞模型（Hybrid Vector Hysteresis Model，HVHM），拓宽了经典模型的适用范围，结合了二者的优点，更精确的模拟磁材料矢量磁滞特性。

HVHM 的建模基础是定义矢量磁滞算子，模型将磁滞算子定义为H 面内的一个由封闭的临界面包围的区域，每个磁滞算子有一个特定的临界面。不同的材料具有临界面的形状不同，二维情况下，各向异性材料的临界面为椭圆形（PSW 模型），长轴为难磁化轴，短轴为易轴；各向同性材料的临界面为圆形（RVM 模型[13]）。每个磁滞算子正则化处理后的磁化强度具有单位幅值，当对其施加外场时，磁化强度大小不变，方向随外场变化发生转动。

根据HVHM 的建模思想，从能量角度出发，利用S-W 建模原理分析了磁性粒子处于磁化稳定状态的条件，借助于磁性粒子产生的矢量场的等势线方程，分别给出了各向异性和各向同性材料磁滞算子的临界线方程，将混合矢量磁滞模型中的磁滞算子定义为由等势线包围的封闭区域，具有单位磁化强度，磁化方向可以随外场方向变化发生转动。假定外场在磁滞算子临界线内部时对磁化方向没有影响，当外场在临界面内部时，磁化方向与磁滞算子原磁化方向相同，直到外场穿出临界面，磁化方向发生巴克豪森跃变，转到由外场决定的磁化方向上，总磁化强度等于所有磁滞算子磁化强度的矢量和。

2 磁性粒子及等势线

考虑由单畴单轴各向异性的磁性材料组成的椭球形磁性粒子，假定粒子沿各向异性轴磁化到饱和状态，可以用磁化强度M 来描述其磁化状态，也可以用单位矢量m=M/MS描述。粒子所具有的特性由单轴各向异性能和外场能-μ0M·Ha控制，定义各向异性轴为易轴（x 轴为易轴），零外场时，磁化强度与易轴同向，施加外场后，磁化强度由易轴方向向外场方向转动。磁化强度、外场和易轴的关系如图1 所示。

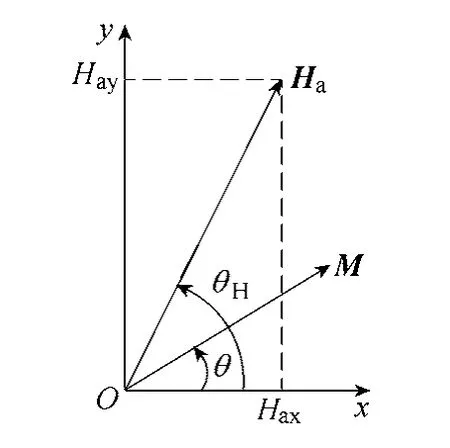
图1 外场Ha、磁化强度M 与易轴间的关系 Fig.1 The relations between applied field Ha ,magnetization vector M and easy axis

磁性粒子的总自由能等于单轴各向异性能加外场能[3]，表达式如式（1）所示。

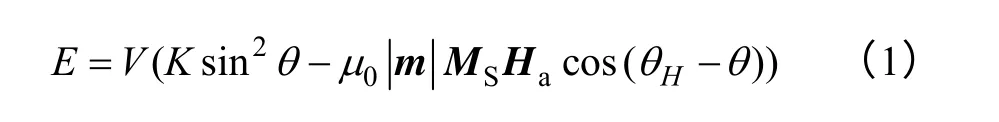
式中，V 为磁性粒子的体积；K 为粒子各向异性常数；θ 和θH分别为磁化强度M、外场Ha与易轴间的夹角。该方程具有一个状态变量θ，两个控制变量θH和Ha。

为了方便计算，给出简化方程

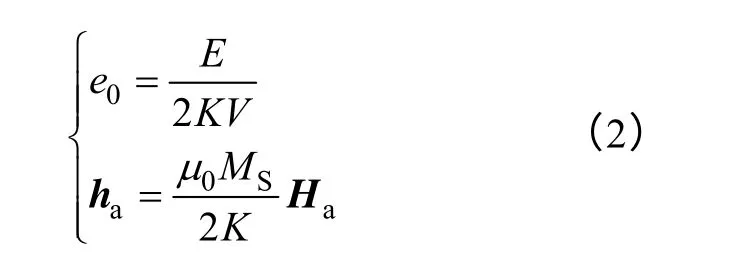
式中，e0为简化后的总能量。

使用式（2）对式（1）进行简化处理，并用ha沿坐标轴的两个分量hx和hy表示外加磁场，式（1）可以改写为式（3）。

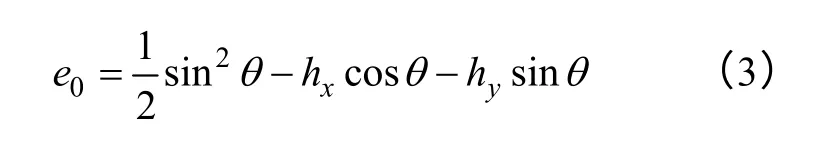
磁化稳定状态发生在自由能取最小值的时候，即能量方程满足能量取最小值条件，计算式（3）的一阶导数并强加条件∂e0/∂θ =0 得能量方程取最小值的条件如式（4）所示。

结合式（3）和式（4），分别用hx和hy表示外场代入能量方程，由de0=0 得单个磁性粒子产生的矢量场的等势线方程为

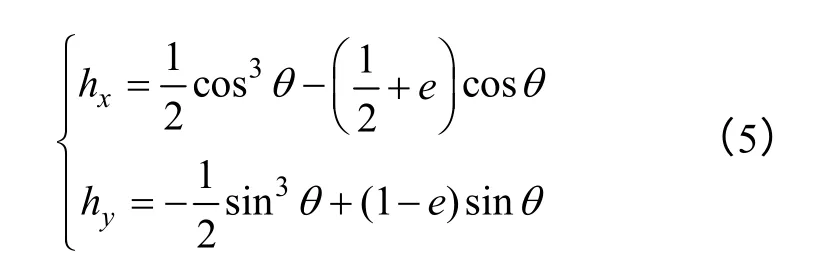
式中，e 为等势线上的能量的固定值。

由于沿等势线的能量变化量恒等于零，当外场沿等势线变化 dha时相对应粒子自由能的变化量deeq= -μ0m·dha= 0，所以当外场沿等势线变化时，粒子的磁化方向垂直于等势线。磁力线是外场平面内所有参考点上磁化强度的切线，因此磁力线垂直于等势面。

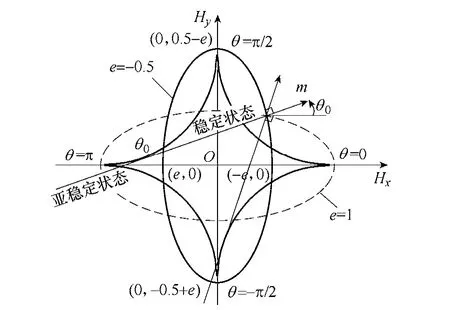
图2 S-W 模型星形判定法则示意图（椭圆型曲线为 等势线，其中实曲线e = -0.5，虚曲线e = 1） Fig.2 The diagram for asteroid rule of the S-W model (The elliptical curve is the equipotential curves,the solid curve:e = -0.5,the dotted curve:e = 1)

图2 中的星形线是粒子能量方程取最大值或最小值的临界曲线，S-W 模型星形判定法则表明[3]，H 面内某点的磁化方向为星形线的切线方向，然后根据该点与星形线的位置关系确定磁化稳定状态下的磁化方向。由星形判定法则和磁力线垂直于等势面（如图2 所示）可得，e＞1 时等势线上的点都处于亚稳定状态；-0.5＜e＜1 时与横轴相交的等势线上的点都处于稳定状态，与纵轴相交的等势线上的点都处于亚稳定状态；e＜-0.5 时等势线上的点都处于稳定状态。

3 磁滞算子定义

在HVHM 中磁滞算子的定义是非常重要的，对各向异性材料，每条主轴的磁特性均不同，只有一条主轴为易轴。本文选用处于平衡状态的等势线方程，即式（5）中的参数e 取值范围为e＜-0.5，作为磁滞算子临界面方程，每个磁滞算子都是由一个特定的等势线包围的区域，具有单位磁化强度，临界面上每一点上的磁化方向沿该点的外法线方向。根据混合矢量磁滞模型建模原理，假定当外场进入临界面时，磁化方向被固定在穿入点时的磁化方向上，直到外场穿出临界面时，磁化方向发生巴克豪森跃变，突变到临界面的法线方向上。

图3 给出了不同θH下的磁滞算子在两个坐标轴上的磁滞回线Mx-Hx和My-Hy。外场取不同方向时，算子磁化强度在坐标轴上的两个分量的开关阈值不同；外场与短轴夹角越小，磁滞损耗越小，越容易磁化；外场与长轴夹角越小，磁滞损耗越大，越难被磁化，即短轴为磁滞算子的易磁化轴，长轴为难磁化轴。选用等势线方程作为各向异性材料的磁滞算子临界面方程。

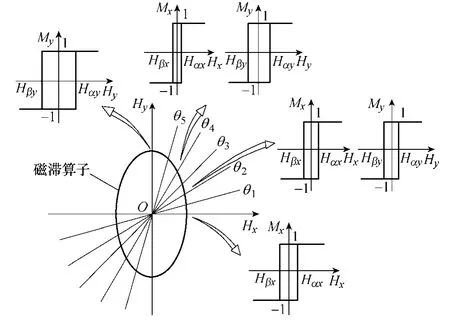
图3 不同θH 下磁滞算子在x-和y-轴方向上的磁滞回线 Fig.3 Hysteresis loops of x- and y-component of magnetization for alternate magnetizations with different θH

对于各向同性材料，不存在各向异性能，粒子性能由外场能控制，表示为

粒子产生的等势线方程为

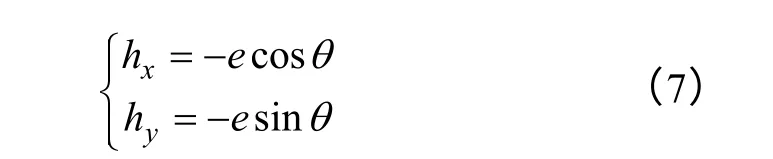
等势线是半径为-e 的圆形，用等势线方程定义各向同性材料磁滞算子临界面方程，磁滞算子是由一个个半径不等的圆形包围的圆形区域，当外场沿等势线变化时，粒子的磁化方向垂直于临界面，临界面是圆形的，磁化方向沿从圆心指向参考点的径向方向，和RVM 模型相同[13]。

4 磁化过程分析

4.1 交变磁化

对磁滞算子施加交变磁化场，计算其磁化过程，这里只给出了各向异性材料磁滞算子的磁化过程。如图4 所示，当外加磁场沿图中所给磁化路径A-B-A变化时，磁滞算子被交变磁化，磁化强度沿坐标轴的两个分量与外场两个分量之间的关系曲线如图5所示。可以看到，当外场穿入临界面后，磁化强度方向保持不变，直到外场穿出临界面，磁化强度方向发生突变，转到穿出点的法线方向上。单个磁性粒子的饱和磁化矢量m 的绝对值为1。

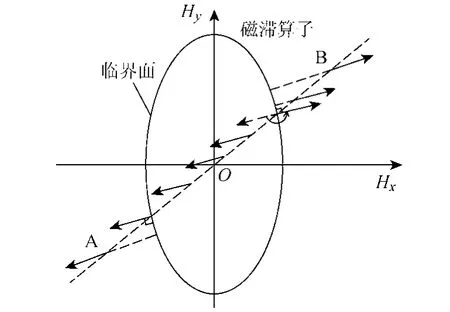
图4 单个磁滞算子及交变磁化路径A-B-A Fig.4 A hysteron with a magnetic path A-B-A

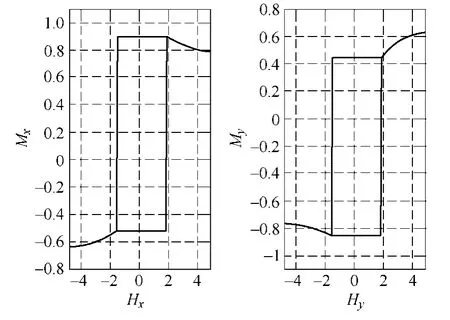
图5 外场沿A-B-A 变化时磁滞算子的磁化回线 Fig.5 The corresponding Hysteresis loop

为了使模型更具一般性，考虑多个相互影响磁滞算子，如图6 所示，给出了三个考虑了相互影响场影响的磁滞算子和两个不同方向的交变磁化路径。考虑粒子间相互影响场时，粒子所面临的总磁场等于外场与影响场的矢量和，可以表示为

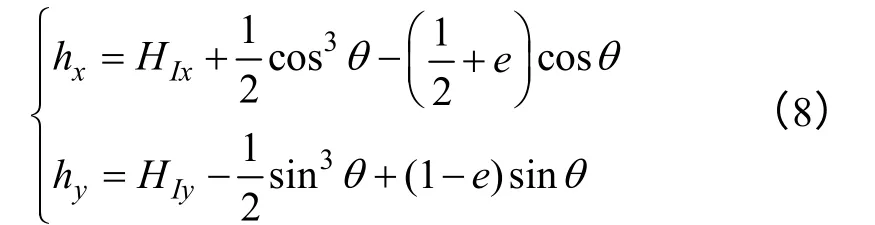
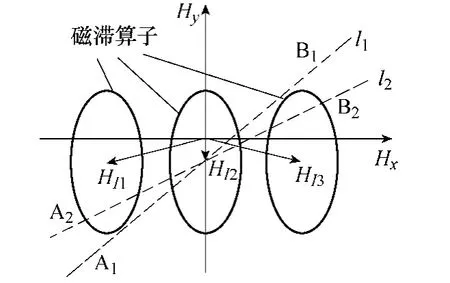
图6 三个磁滞算子及两个不同的交变磁化路径 Fig.6 Three hysterons with two different magnetic paths

为了方便计算，将磁滞算子中心从原点做一个矢量位移，移到（HIx,HIy）处，这样临界面方程和不考虑影响场的相同，只是中心位置发生了变动，如图6 所示。总磁化强度沿坐标轴的分量分别等于所有磁滞算子的磁化强度沿坐标轴分量的矢量和。当外加磁场沿图 6 所示的磁化路径 A1-B1-A1与A2-B2-A2变化时，磁化强度分量与外场分量之间的关系曲线如图7 与图8 所示。由图7、图8 可以看到，外场与磁滞算子相交时发生巴克豪森跃变，产生磁滞损耗。

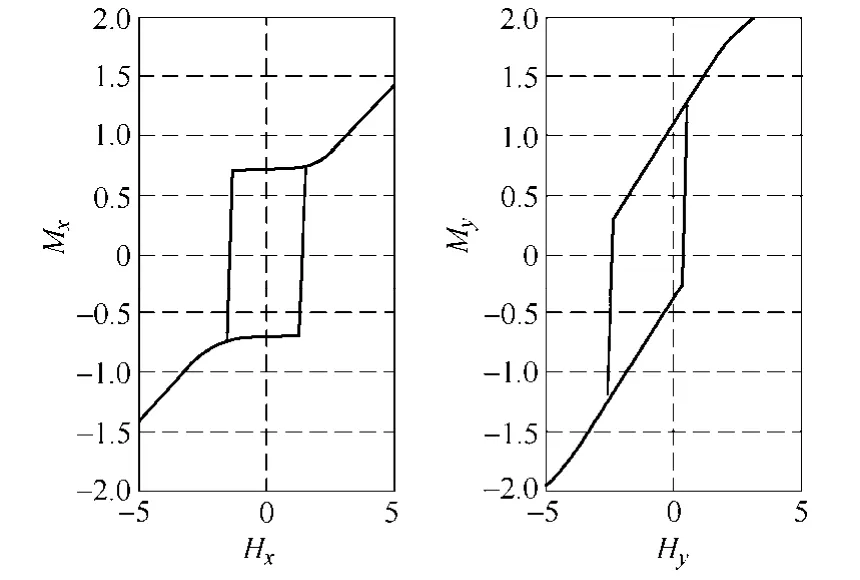
图7 沿A1-B1-A1 的磁化回线 Fig.7 The magnetic loops correspond to path A1-B1-A1

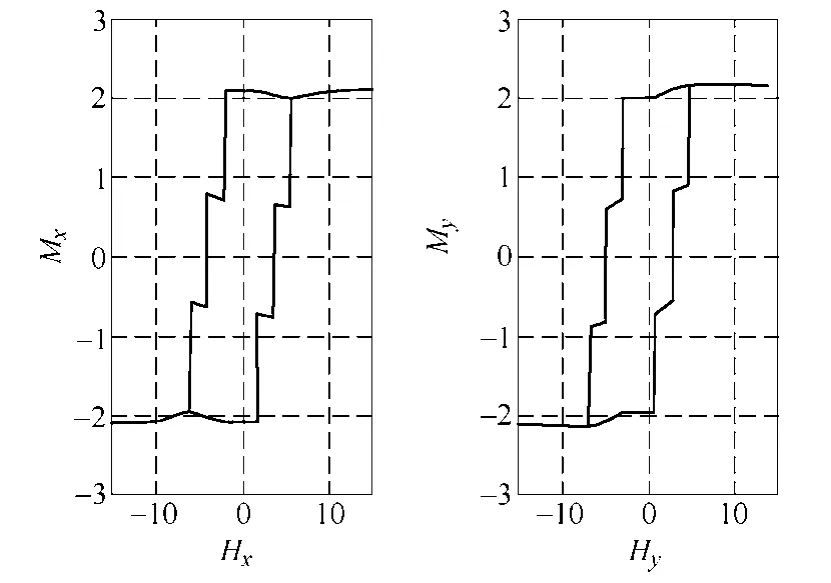
图8 沿A2-B2-A2 的磁化回线 Fig.8 The magnetic loops correspond to path A2-B2-A2

4.2 旋转磁化

在旋转激磁条件下，可分析各向异性材料磁滞算子的旋转磁化特性。如图9 所示，当外场分别沿逆时针方向变化的圆形磁化路径C、D、E 对磁滞算子进行旋转磁化时，磁化强度分量与外场分量之间的关系曲线如图10 所示。由图10 所示的磁化曲线可以看到，当磁化路径与磁滞算子相交时，会产生磁滞。图9 中磁化路径C、D 都与磁滞算子有相交部分，与之相对应的磁化曲线具有明显的磁滞现象，即只要磁化路径穿出磁滞算子临界面，就会发生巴克豪森跃变，产生磁滞损耗；而对于图9 所给出的三个磁滞算子来说，沿磁化路径E 变化的外场足够大，磁化方向与外场方向相同，计算所得的磁化回线与所施加外场的回线形状相同，没有磁滞损耗。

图9 三个分别从C、D、E 开始的 逆时针变化圆形磁化路径 Fig.9 Three different counterclockwise circulars applied magnetic field paths:starting from C、D、E

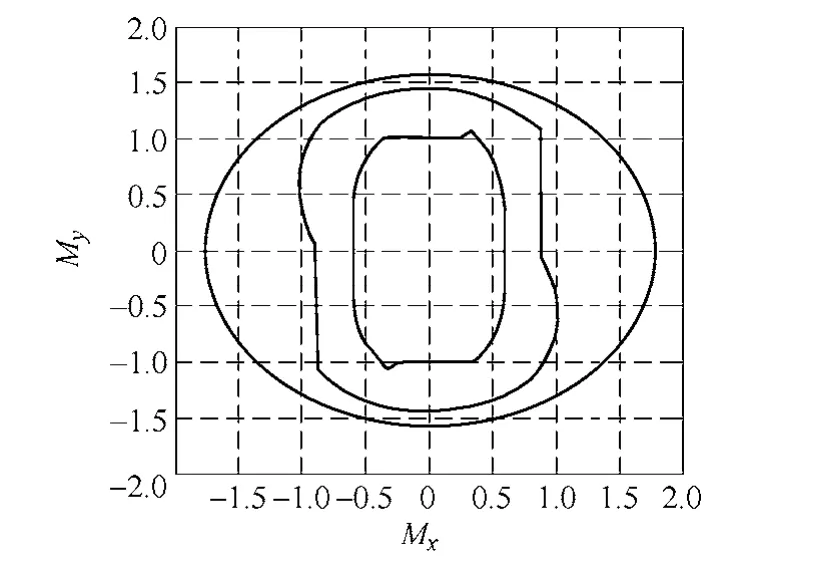
图10 对应的磁化回线 Fig.10 The corresponding hysteresis loops

5 磁滞算子特性分析

5.1 损耗特性

由磁滞算子临界面方程可得，当θ = 0°或180°时，磁滞算子的临界面与x 轴上的交点为hx= -e 和hx= e；当θ = 90°或-90°时，磁滞算子的临界面与y 轴的交点为hy=0.5-e 和hy=-(0.5-e)，如图2 所示。磁滞算子的临界面的x 轴截距与y 轴截距之间的关系可以表示为

则磁滞算子的临界面的轴长比为

随外场增大，A 逐渐趋向于1，磁滞算子的临界面近似为圆形，说明当外场足够大时，各向异性材料的磁化特性和各向同性材料相近，磁化方向近似与外场方向相同。

在旋转外场下，当外加磁场足够大时，磁滞算子完全包含在激磁场中，临界面与外场没有相交部分，磁化方向与外场方向相同，不产生磁滞损耗，模型具有损耗特性。

5.2 热力学第二定律

混合矢量磁滞模型中磁滞算子的能量变化要满足热力学第二定律：任意一个与磁滞算子临界面相交的封闭路径必定存在能量损耗[19]。也就是说，磁滞算子沿任意一个穿过临界面的封闭磁化路径的能量变化必须小于等于零。如图11 给出了一个磁滞算子和一条任意封闭的磁化路径γ，P1、P2分别为γ与临界面的两个交点，P1为穿入点，P2为穿出点。磁滞算子的临界面是一条等势线，且当外场穿入临界面时不发生能量损耗，因此磁滞算子外部的任意一条连接穿入点P1和穿出点P2的磁化路径γ-out 的能量变化为Eγ-out=0。而当外场在磁滞算子内部时，外场对强化强度没有影响，磁化方向被固定在穿入点P1处的磁化方向上，不产生能量变化，直到外场 穿出临界面时，磁化方向在穿出点P2处发生巴克豪森跃变，产生能量损耗，因此，沿临界面内部任意一条从P1点到P2点的磁化路径γ-in 的能量变化为Eγ-in＜0。封闭磁化路径γ 的能量变化为Eγ= Eγ-out+ Eγ-in＜0，磁滞算子的能量变化满足热力学第二定律。

图11 二维矢量磁滞算子满足热力学第二定律 Fig.11 The congruence of the 2D hysteron with the second principle of the thermodynamics

5.3 擦除特性

模型的磁化过程与磁化路径及其在临界面上的穿入穿出点有关，具有磁化历史擦除特性。如图12所示，沿从原点到P1点的磁化路径α 对磁滞算子磁化，P1点的磁化强度取决于路径α 穿入临界面的穿入点；沿从P1点到P2点的磁化路径β1继续对磁滞算子进行磁化，由于P1点、P2点及路径β1都是在磁滞算子内部，所以P2点的磁化强度依旧依赖于路径α；沿从P2点到P3点的磁化路径β1继续对磁滞算子进行磁化，路径β2与临界面有穿出点，P3的磁化强度不再取决于路径α，而是取决于路径β2的穿出点，路径α 产生的磁化效果已被路径β2擦除。

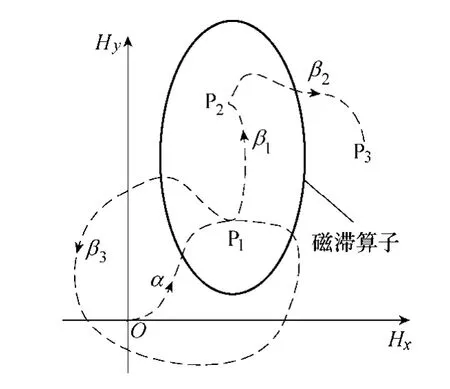
图12 二维矢量磁滞算子擦除特性 Fig.12 The deletion property of the 2D hysteron

若沿路径α 对磁滞算子磁化之后，再沿穿过P1点的封闭路径β3继续对磁滞算子磁化，P1点的磁化强度只取决于路径β3的穿入点，与路径α 无关，路径α 产生的磁化效果已经被新的路径β3擦除。

单个磁滞算子具有擦除特性，但不具备 Man- delung 定则[21]中的返回点记忆特性，只有同时考虑多个磁滞算子的磁化过程时，模型才符合描述磁滞特性的Mandelung 定则。

6 总结

从能量角度出发，提出了HVHM 模型中二维矢量磁滞算子一种定义方法，分别给出了各向异性和各向同性材料磁滞算子的临界面方程，结合S-W 模型星形判定法则，确定了外场在磁滞算子临界面外部时磁化方向沿临界面法线方向，外场在临界面内部时磁化方向被固定在穿入点处的磁化方向上。

计算分析了在交变磁化场和旋转磁化场中磁滞算子的磁化过程，当外场与磁滞算子相交时，产生磁滞损耗，当外场值足够大时，磁化方向与外场同向，没有磁滞损耗。对磁滞算子的特性分析表明，磁滞算子满足热力学第二定律，具有损耗和擦除特性，满足描述磁滞特性的Mandelung 定则。该定义方法有助于精确模拟磁化过程、提高矢量磁滞模型的有效性和可靠性，为提高变压器、电机等电工装置运行效率并降低能耗奠定了理论基础。

[1] Preisach F.Über die magnetische nachwirkung[J].Zeitschrift Für Physik,1935,94(5-6):277-302.

[2] Coleman B D,Hodgdon M L.A constitutive relation for rate-independent hysteresis in ferro-magnetically soft materials[J].International Journal of Engineering Science,1986,24(6):897-919.

[3] Stoner E C,Wohlfarth E P.A mechanism of magnetic hysteresis in heterogeneous alloys[J].IEEE Transactions on Magnetics,1991,27(4):3475-3518.

[4] Jiles D C,Atherton D L.Theory of ferromagnetic hysteresis[J].Journal of Magnetism and Magnetic Materials,1986,61(1):48-60.

[5] Mayergoyz I D.Mathematical models of hysteresis [M].New York:Springer Verlag,1991.

[6] Della Torre E.Magnetic hysteresis[M].New York:IEEE Press,1999.

[7] Michelakis C,Litsardakis G,Samaras D.A contribu- tion to 2D vector preisach modelling[J].Journal of Magnetism and Magnetic Materials,1996,157:347- 348.

[8] Koh C S,Hahn S,Park G S.Vector hysteresis modeling by combining stoner-wohlfarth and preisach models [J].IEEE Transactions on Magnetics,2000,36(4):1254-1257.

[9] Della Torre E,Pinzaglia E,Cardelli E.Vector modeling- part I:Generalized hysteresis model[J].Physica B:Condensed Matter,2006,372(1):111-114.

[10] Della Torre E,Pinzaglia E,Cardelli E.Vector modeling- part II:ellipsoidal vector hysteresis model,numerical application to a 2D case[J].Physica B:Condensed Matter,2006,372(1):115-119.

[11] Della Torre E,Cardelli E.A preisach-stoner-wohlfarth vector model[J].IEEE Transactions on Magnetics,2006,42(10):3126-3128.

[12] Kahler G R,Della Torre E,Cardelli E.Implementation of the preisach-stoner-wohlfarth classical vector model [J].IEEE Transactions on Magnetics,2010,46(1):21-28.

[13] Cardelli E,Della Torre E,Pinzaglia E.Magnetic energy and radial vector model of hysteresis[J].Journal of Applied Physics,2006,99(8):08D703-08D703-3.

[14] Della Torre E,Cardelli E,Bennett L H.Identifying hysteresis losses in magnetic media[J].IEEE Transac- tions on Magnetics,2010,46(11):3844-3847.

[15] Della Torre E,Bennett L H,Jin Y.An effect of particle size on the behavior of ferromagnetic materials [J].Journal of Magnetism and Magnetic Materials,2012,324(14):2189-2192.

[16] Cardelli E,Della Torre E,Faba A.Properties of a class of vector hysteron models[J].Journal of Applied Physics,2008,103(7):07D927-07D927-3.

[17] Cardelli E,Della Torre E,Faba A.Analysis of a unit magnetic particle via the DPC model[J].IEEE Transac- tions on Magnetics,2009,45(11):5192-5195.

[18] Cardelli E,Della Torre E,Faba A.Numerical imple- mentation of the DPC model[J].IEEE Transactions on Magnetics,2009,45(3):1186-1189.

[19] Cardelli E.A general hysteresis operator for the mode- ling of vector fields[J].IEEE Transactions on Magnetics,2011,47(8):2056-2067.

[20] Cardelli E,Della Torre E,Faba A.A general vector hysteresis operator:Extension to the 3-D case[J].IEEE Transactions on Magnetics,2010,46(12):3990-4000.

[21] Mandelung E.On the magnetization by fast current and an operation principle of the magneto-detectors of rut herford-marconi[J].Ann Phys,1905,17:861-890.