新型感应式电能传输系统高效拾取机构的仿真设计

马林森 李砚玲 麦瑞坤 何正友 黄立敏

（西南交通大学电气工程学院电力信息研究室 四川省 成都市 610031）

1 引言

传统用电设备的电能都是以直接的电气连接实现能量传输，这种直接的电气连接方式存在电线裸露、漏电等安全隐患，使得这种供电方式难以适应多变的环境，例如湿度、温度等因素的剧烈变化。因此，环境适应性好、安全可靠、灵活安全的非接触供电方式日益受到人们的青睐。非接触供电技术包括感应式、微波式、共振式等多种实现方式，本文着重分析感应式电能传输（Inductive Power Transfer，IPT）系统，考虑到拾取机构在IPT 系统中担负着将电源侧的电能无线传递给负载侧的重任，直接影响着系统的能量输出，是IPT 系统稳定运行的关键，因此有必要对拾取机构进行深入的分析[5,6]。

本文首先建立IPT 系统拾取机构的电路及磁路模型，依据传输电压和传输功率等机构设计指标，分析比较不同拾取机构的优劣，结合软件有限元仿真的方法提出一种新型的高效拾取机构模型。

2 拾取机构电路模型分析

图1 所示的U 型松耦合变压器模型是一种简单的IPT 系统拾取机构模型，考虑到常用的电力变压器模型是紧耦合的，其漏感很小，一般可忽略不计，原边电压和次边电压满足匝比关系。但是在IPT 系统中，其拾取机构通过松耦合的方式实现能量传输，空气气隙的存在使得其耦合性能差，次边感应电压与原边电压间不存在匝数比关系，同时由于松耦合变压器中的励磁电感和励磁电流都无法直接测得，因此采用如图2 所示的互感模型，相对于传统变压器模型而言更适用于IPT 系统拾取机构的建模。

图1 U 型松耦合变压器模型Fig.1 U type loosely coupled transformer model

图2 互感电路模型Fig.2 Mutual inductance model

根据磁感应关系可以得到拾取机构原边和次边电压的关系，其表达式如下:

Φ1、Φ2表示原边电感产生的磁场，ΦM1、ΦM2分别表示原边与次边的共磁链，i1、i2分别表示原边和次边的电流强度。

采用相量描述的形式，可将次边开路感应电压表示为:

其中Vp表示等效高频交变电源，是原边侧高频磁场产生的部分；Lp、Ls表示能量发射线圈的等效电感，Cp、Cs表示等效电感的补偿电容；Rp、Rs表示导轨线圈和拾取机构的内阻；M为导轨线圈Lp与拾取线圈电感Ls之间的互感；Ip为原边导轨电流有效值；R 表示次边的等效阻抗；Zr表示次边电路映射到原边的等效阻抗。

根据自感、互感与电压之间的关系可以得到图3 中原边绕组电感Lp和次边绕组电感Ls两端电压的有效值[4]分别为:

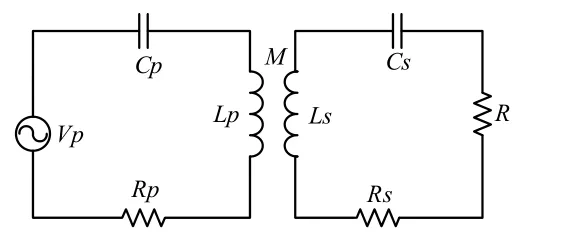
图3 IPT 系统拾取机构等效电路模型Fig.3 Equivalent circuit model of pick-up in IPT system

根据KVL 定律及式（4）与式（5）可以得到图4 中原边和次边的回路方程:

图4 IPT 系统原边和次边的等效电路Fig.4 The equivalent circuit between the primary side and the secondary side

则有效输出功率[3]为:

次边在原边的映射阻抗Zr

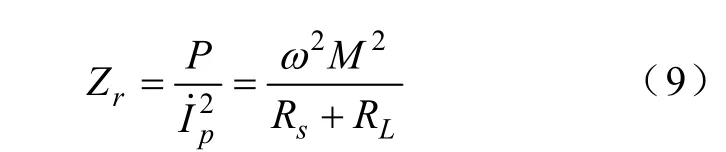
在恒流模式下，通过调节Ip控制系统能量传输，根据式（9），可以得到原边电压有效值:

由式（11）和式（12）可以得到最终的IPT 系统拾取机构传输功率表达式:

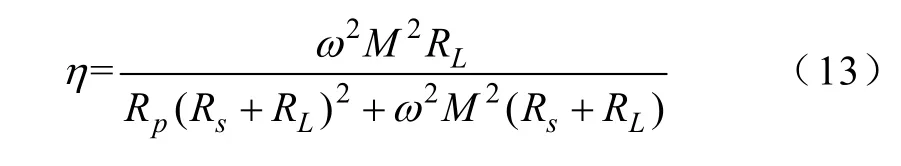
根据式（13）对IPT 系统的传输效率分析，可得以下结论:

1）在负载一定的情况下，即Rp为定值，系统效率与ω2M2成正相关；对于工作频率f 确定的IPT系统而言，系统传输效率随着拾取机构互感M 的增大而增大；

2）在IPT 系统拾取机构一定的情况下，由于Rp为定值，且工作频率f 确定，因此IPT 系统传输效率随着负载的等效电阻增大而减小；

3）在IPT 系统拾取装置和负载一定的情况下，由于Rp为定值，那么传输效率与ω2M2成正相关；对于能量拾取机构来说，原次边的互感M 唯一确定，由ω=2πf 可以得到IPT 系统传输效率随着传能系统的工作频率f 的增大而增大。

4）原、次边电阻的增大会降低系统的传输效率，因此，要增大整个传输系统的能量传输效率要确保原边和次边谐振频率一致，使得原边和次边的内阻最小。

根据上述对IPT 系统分析，对于不同负载而言能量传输效率均有不同，且不同负载都存在一个最大效率传输参数；因此在针对不同的负载需要设计不同的拾取机构参数，以满足传输效率最优。当负载一定的情况下，IPT 系统传输效率随着系统互感M 的增大而增大，且次边的开路电压与互感M 成正比，因此可将次边的开路电压作为衡量拾取机构优劣的性能指标。

3 拾取机构磁路模型分析

将图1 松耦合变压器模型等效为图5 所示松耦合变压器等效磁路，以分析松耦合变压器的磁路特性，其中，原边、次边磁动势为Fp、Fs，原边、次边铁芯磁阻为Rcp、Rcs，气隙磁阻为Rσ1、Rσ2，原边、次边漏磁阻为Rpσ、Rsσ。

图5 松耦合变压器的等效磁路Fig.5 Equivalent magnetic circuit of the loosely coupled transformer

根据等效磁路[1]可知，电路中漏磁、空气磁阻直接影响了电路的互感特性，进而影响磁通量使得次边感应电压变化；由此降低空气磁阻和磁芯磁阻可以增加磁通量，达到增大感应电压的目的；一般来说，通过减小磁路距离和增大空气截面积的方式可以减小空气磁阻，磁芯可以选择磁导率大的磁性材料可以达到减小磁芯磁阻。

铁芯磁阻可表征为:

式（14）中μ0表示空气磁导率，μr表示铁芯的相对磁导率，S 表示铁芯的横截面积，l 表示铁心等效磁芯长度。

对于空气磁阻可表示为:

S 表示有效的空气的横截面积，l 表示空气气隙长度。

由式（14）和式（15）可以看出对于电磁机构的磁芯结构来说增大磁导率、增大铁芯的横截面积、增大磁芯的相对磁导率都可以降低磁芯的磁阻。一般铁氧体的相对磁导率是几百，若铁氧体的磁导率足够大那么磁芯的磁阻可忽略不计，环路的磁阻只有空气磁阻；减小磁芯的宽度和增大磁芯的横截面积均可以有效减少磁芯磁阻。对于E 型磁芯，当磁芯的长度固定，两条支路的磁芯宽度逐渐增大会使得磁柱间的距离逐渐减小，若磁芯的中心磁柱与侧磁柱间的空气气隙减小会使得漏磁阻减小，这样就增加了漏磁通，在一定程度上使得原边和次边互感降低，因此在设计磁路机构的过程中要兼顾漏磁通、原边和次边之间的互感大小，统筹分配两者间的大小关系，因此给定拾取机构的宽度设计合理的磁芯的横截面积是十分重要的。

4 拾取机构仿真设计

4.1 传统拾取机构分析

针对一套工作频率设定为20kHz 的面向电动车动态取电的IPT 系统作为仿真设计的对象，以系统中实际的拾取机构参数作为仿真参数模型。

首先分析传统的E 型和U 型磁路机构模型[2]。其磁芯跨双轨的模型如图6 和图7 示，设定原边双轨的电流值I=10A，轨道间距设定为50mm，磁芯材料为普通的铁氧体材料，相对磁导率为500。对于E 型磁芯机构，次级线圈导线绕在中柱上，设定绕7 匝；对于U 型磁芯机构，次级线圈导线绕在中间横梁上，设定两边各绕3.5 匝。

图6 E 型磁芯结构图Fig.6 E type magnetic core structure

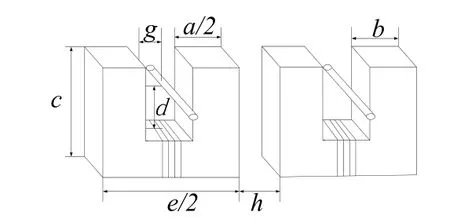
图7 U 型磁芯结构图Fig.7 U type magnetic core structure

在Ansoft Maxwell 3D 仿真软件中建立仿真模型，其数据参数如下:a=40mm，b=20mm，c=63mm，e=132mm，f=40mm，h=0mm。模型以垂直距离 d和侧移距离g 作为模型的两个参考变量对比原次边的互感值。

忽略原边和次边的内阻影响，通过 Ansoft Maxwell 3D 得到不同模型机构的磁芯的在不同工况下的互感值代入到如图8 所示的理想IPT 等效电路图中，分析IPT 系统的次边开路感应电压的变化情况。

图8 仿真原理电路Fig.8 The principle diagram of the simulation circuit

根据图9 和图10 所示的仿真结果对比分析E型和U 型磁芯的次边拾取电压得到几点结论:

图9 次边开路电压随侧移距离变化曲线Fig.9 Open-circuit voltage of the secondary side as the lateral distance changes

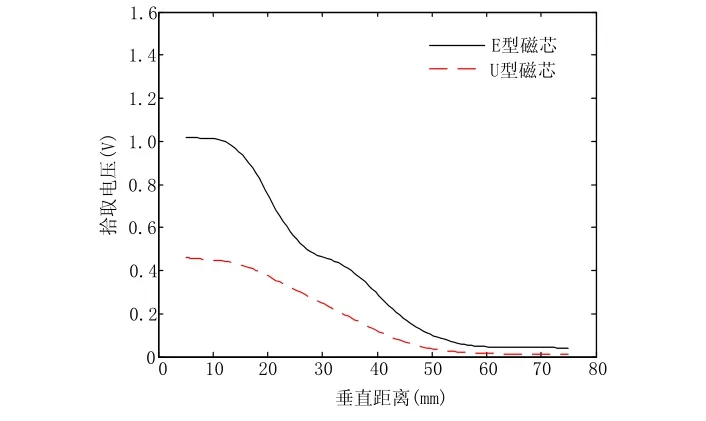
图10 次边开路电压随垂直距离变化曲线Fig.10 Open-circuit voltage of the secondary side as the vertical distance changes

1）当次边拾取机构有小微量侧移时，拾取电压变化都比较小；随着距离的增大，次边感应电压越来越小。

2）相同的垂直电气距离E 型和U 型磁芯拾取机构，E 型拾取机构的感应电压要大于相同条件的U 型磁芯；

3）相同的侧移电气距离E 型和U 型磁芯拾取机构，U 型拾取机构的感应电压较U 型磁芯平稳。

4.2 新型拾取机构分析

综合考虑了E 型磁芯和U 型磁芯的物理特性，结合E 型磁芯的次边拾取电压大，U 型磁芯的次边拾取电压稳定的优点，将绕组的缠绕位置放在E 型中间磁柱，使次边的感应电压可以得到最大值，同时采取两侧磁柱向内外延伸的方式，以减小侧移时的空气磁阻，来降低侧移距离对拾取机构拾取电压的影响，新型磁芯结构如图11 所示。

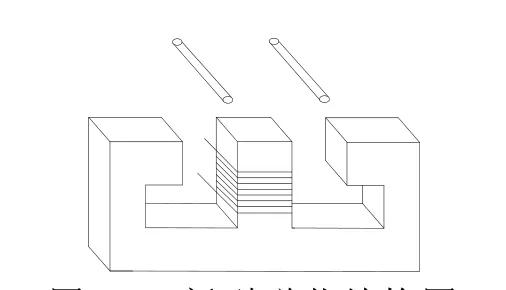
图11 新型磁芯结构图Fig.11 New type magnetic core structure

针对新型磁路机构仿真分析后，与传统的E 型和U 型磁芯结构进行比较，可得到如图12 和图13所示次边开路感应电压曲线。

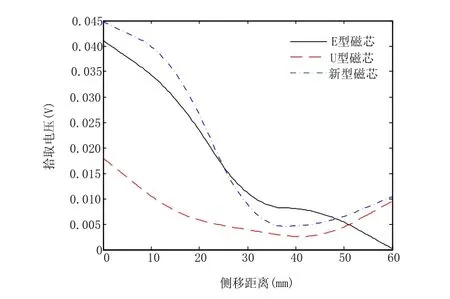
图12 次边开路电压随侧移距离变化曲线Fig.12 Open-circuit voltage of the secondary side as the lateral distance changes

图13 次边开路电压随垂直距离变化曲线Fig.13 Open-circuit voltage of the secondary side as the vertical distance changes

由图12 和图13 可以得出:与传统U 型和E 型磁芯相比，新型拾取机构在垂直距离相同的情况下，次边的感应电压远大于传统磁芯机构；而在在侧移距离比较小时，新型磁路机构的稳定性较传统磁路机构好，随着距离的增大新型磁机构也会有较大的电压压降，但随着距离的增大拾取电压会稳定在一个值上，与传统磁路机构相比稳定性更高，即可以侧移距离对感应电压的影响。

5 结论

本文重点对IPT 系统的拾取机构进行分析，通过分析影响拾取机构感应电压的主要因素，为IPT系统拾取机构的设计和优化提供了思路。在理论分析和仿真分析的基础上，改进了现有的磁芯结构，并对提出的新型磁芯结构进行仿真分析，验证了新型次新结构在传输高效和稳定性方面的优势。

[1]Shin J,Shin S,Kim Y,et al.Design and Implementation of Shaped Magnetic Resonance Based Wireless Power Transfer System for Roadway-Powered Moving Electric Vehicles[J].2013.

[2]张宗明.非接触电能传输系统电磁机构研究[D].重庆大学,2007.Zhang Zongming.Study on electric-magnetic structure of the contactless power transfer system[D].Chongqing University.2007.

[3]夏晨阳,李建功,左兰,等.高能效导轨式 ICPT系统分布式磁路机构研究[J].四川大学学报：工程科学版,2012,44(005)：155-160.Xia Chenyang,Li Jiangong,Zuo Lan,et al.Research on distributed magnetic circuit for rail-type ICPT system[J].Journal of Sichuan University：Engineering Science Edition,2012,44(005)：155-160.

[4]何秀,颜国正,马官营.互感系数的影响因素及其对无线能量传输系统效率的影响[J].测控技术,2007(11)：57-60.He Xiu,Yan Guozheng,Ma Guanying.Mutual inductance’s affecting factors and its affection to the energy transmission efficiency of wireless energy transmission system[J].Measurement and Control Technology,2007(11)：57-60.

[5]黄学良,谭林林,陈中,等.无线电能传输技术研究与应用综述[J].电工技术学报,2013,28(10)：1-11.Huang Xueliang,Tan Linlin,Chen Zhong,et al.Review and Research Progress on Wireless Power Transfer Technology[J].Transctions of China Electrotechnical Society,2013,28(10)：1-11.

[6]戴卫力,费峻涛,肖建康,等.无线电能传输技术综述及应用前景[J].电气技术,2010(07)：1-6.Dai Weili,Fei Juntao,Xiao Jiankang,et al.An overview and application prospect of wireless power transmission technology[J].Electrical Engineering.2010(07)：1-6.