永磁同步电动机矢量控制研究

李星星，邓福军

(大连交通大学 电气信息学院，辽宁 大连 116028)*

0 引言

永磁同步电动机(PMSM)具有结构简单、运行可靠、体积小、质量轻、效率高等优点，广泛的应用与航空航天、国防、工农业生产和日常生活的各个领域［1］.先进自动控制理论与PMSM结合组成的电机控制系统广泛的应用于高精度、快速响应的场合.本文针对凸极式永磁电动机的Ld≠Lq的特性，研究了矢量控制下的最大转矩电流比控制，即在相同电流下可输出最大转矩的控制方法.文献［2］通过求解高次方程组推导出电磁转矩与d、q轴电流线性关系，通过线性控制实现最大转矩电流比控制，高次方程组求解过程复杂并且占用大量的运算空间.文献［3］通过反馈思想来求解高次方程组，实际运用中用查表实现控制，同样运算过程复杂.为便于工程实践，本文给出改进的工程求解方法，采用改进的曲线拟合方法求解误差最小的电磁转矩与d、q轴电流关系的关系式.文中对id=0控制、最大转矩电流比控制及其近似算法进行比较，仿真结果表明:该方法可有效提高系统的动态性能，具有很好的工程应用性.

1 PMSM数学模型

PMSM在d-q坐标系下的数学模型为:

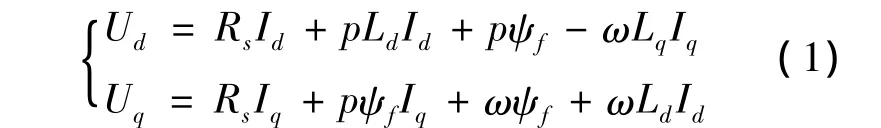
转矩方程为:

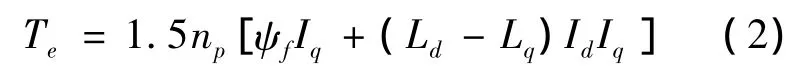
式中:Ud，Uq分别为 d，q轴电压;Id，Iq分别为 d，q轴电流;Ld，Lq分别为d，q轴电感;Rs为定子电阻;ψf为永磁体磁链;ω为转子电角速度;Te为电磁转矩;np为电机极对数;p为微分算子.

由式(2)可以看出，PMSM的输出转矩只取决于d轴电流分量和q轴电流分量，改变Id，Iq的数值可以实现对转矩的控制.电磁转矩前一部分称为永磁转矩，后一部分称为磁阻转矩.电机一般采用id=0的控制方法，但是这种方法忽略了磁阻转矩的作用，使剩余转矩与电流成线性关系，此时电磁转矩方程变为

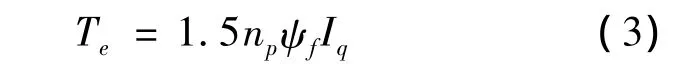
对于隐极式PMSM而言，Ld和Lq相等，电磁转矩只与Iq有关，常采用此策略进行控制.但对于凸极式PMSM，为充分利用磁阻转矩，常采用最大转矩电流比控制［4-7］.

2 最大转矩电流比控制

id=0控制方法对于凸极式永磁电动机而言，在电机输出相同的转矩下，电机的定子电流并不是最小的，因此，采用最大转矩电流比控制方法，使得电机在输出相同情况下电流最小，从而损耗最小.

设永磁同步电动机运转时其定子的三相电流为

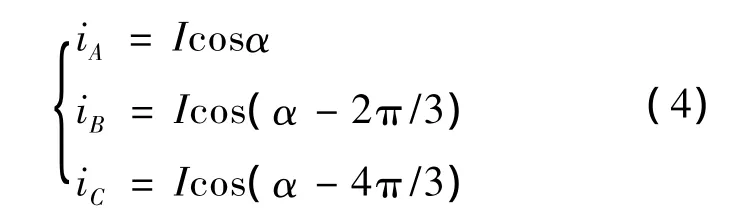
式中，iA、iB、iC分别为电机 A、B、C 相定子电流;I为电机定子电流幅值;α为定子电流矢量与A轴的夹角.

将式(4)进行坐标转换，得到电机d-q轴电流如下

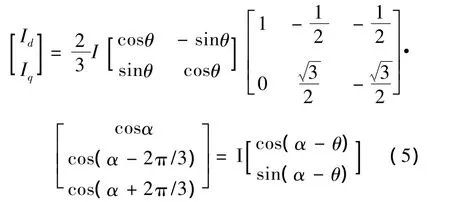
进而有

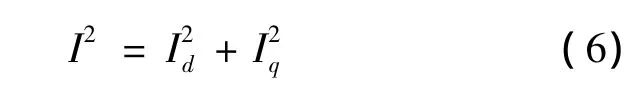
可以看出，最大转矩电流比可转化为如下极值问题

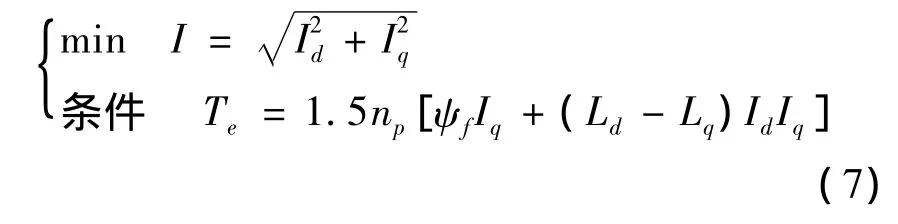
做辅助函数

式中，λ为拉格朗日乘子.

将式(8)分别对Id、Iq和λ求偏导数并令其为零，有

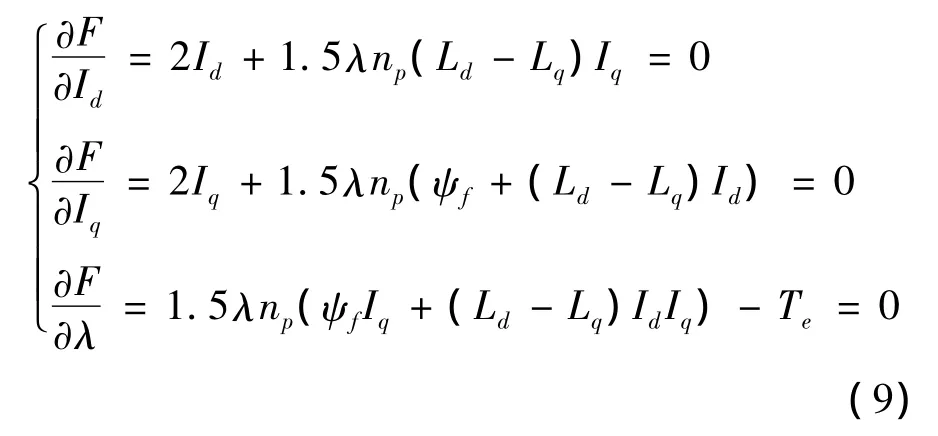
由式(9)可得出:

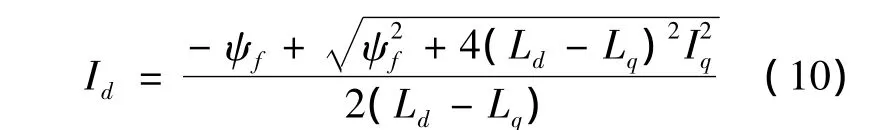
将Id、Iq和Te表示为标幺值，可以得到交、直电流分量与电磁转矩的关系为

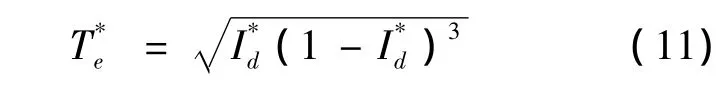
式(10)、(11)为永磁电动机运行时电磁转矩与d、q轴电流的表达式.

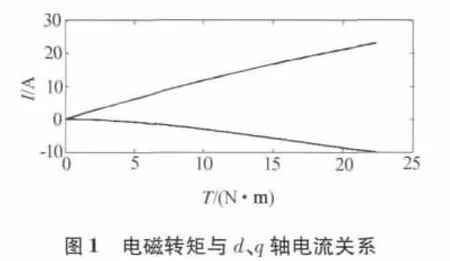
根据最大转矩电流控制的运算，图1给出了凸极式永磁电动机电磁转矩与d、q轴电流的关系曲线，图2给出电磁转矩与定子电流比值的关系曲线.

3 最大转矩电流比的改进工程近似方法

在实际应用中，需要知道d、q轴电流与电磁转矩的关系式，这样给定参考转矩后，就可以求出MTPA运行时的参考电流，但是要反解出电流与电磁转矩的表达式非常困难.在工程运用中，通常是离线计算出最大转矩电流比不同的电磁转矩对应的电流值，采用查表的方法实现MTPA控制，不过要占用大量存储单元.文献［1］讨论了d、q轴电流与电磁转矩的近似线性关系，但是误差较大;文献［8-9］讨论了运用曲线拟合的方法求解精确的表达式，分别采用3次拟合和5次拟合多项式;文献［10］讨论了参数在线估算进行最大转矩电流比控制.

运用式(10)、(11)直接画出电磁转矩与d、q轴电流的函数曲线，接下来运用Matlab曲线拟合进行选取数据，选取不同次数的多项式进行曲线拟合.文献［8-9］都是对d、q轴电流和电磁转矩进行3次或5次拟合，针对不同的电机参数，曲线拟合的次数不同直接决定了控制方式的精度和误差.本文针对特定的电机参数，由于d、q轴电感参数不一样，因此针对交、直轴电流与电磁转矩的表达式分别进行不同次数的拟合，最后分析计算拟合多项式误差，考虑到拟合次数多直接影响控制器计算能力，设定最小误差值，只要拟合多项式在允许误差值，就采用较小的次数进行拟合.

本文中PMSM 参数设置为Rs=2.875 Ω，Ld=6.5 mH，Lq=10.5 mH，np=3，根据不同次数曲线拟合方法和误差分析，得出适合d、q轴的拟合多项式，具体的表达式为

图3表示适合d、q轴的曲线拟合的关系曲线.

图3 电流Id、Iq与转矩拟合曲线关系

4 仿真结果及分析

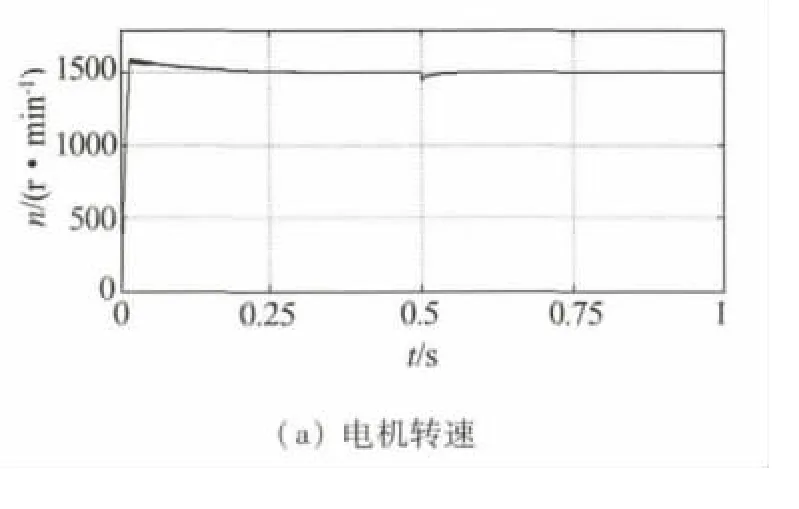
针对上述方法，利用MATLAB/Simulink进行MTPA控制的仿真研究，建立如图4所示的PMSM仿真模型［11-12］，并且与id=0控制仿真相比较.初始速度设为0，转速给定为1 500 r/min.仿真时间为1 s，在0.5 s给定负载6 N·m.

图4 MTPA控制矢量控制原理框图

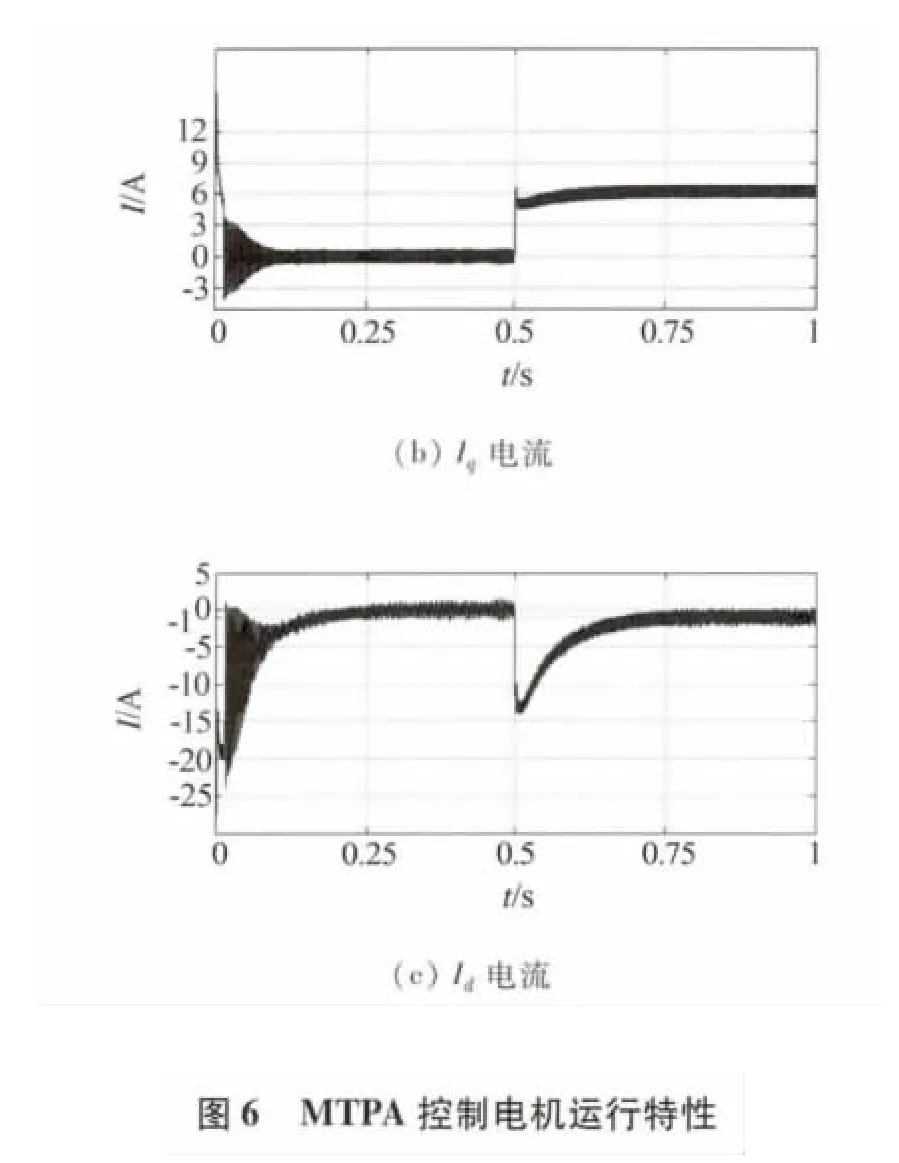
图5给出了采用id=0控制方式的电机运行特性，图6给出采用MTPA控制的电机运行特性.图5(a)和图6(a)为两种控制方案下起动的转速波形，可以看出两者的区别不大，只是采用MTPA控制方式的转速响应快速性比较好.由图5(b)、(c)和图6(b)、(c)可以看出，id=0控制随着负载转矩的增大Id一直不变，无法利用电磁转矩中的磁阻转矩，但是在最大转矩电流比控制下，Id随着负载转矩的增大而反向增大，所以可以有效地利用磁阻转矩，对于相同的负载转矩，id=0控制方式中Iq=8A，而在MTPA控制方式中，电机Iq=6A、Id=-1A，定子电流比前者电流要小，达到应用最小的电流达到转矩的目的，减少了电机损耗.

5 结论

本文对凸极式PMSM矢量控制的MTPA进行研究，讨论总结出适合工程实际的近似方法.MTPA控制相对于id=0控制可以有效的减小电机定子电流，减少损耗，但是算法相对复杂.本文提出的改进曲线拟合方法，把d、q轴电流表达式的误差减小到最小，提高运算精度同时减少运算复杂程度，实现最快最精确的MTPA永磁电动机控制.

［1］唐任远.现代永磁电机理论与设计［M］.北京:机械工业出版社，2012:3-9.

［2］李长红，陈明俊，吴小役.PMSM调速系统中最大转矩电流比控制方法的研究［J］.中国电机工程学报，2005，21:169-172.

［3］徐佳园.永磁同步电机最大转矩电流比控制［D］.北京:北京交通大学，2010:28-35.

［4］连琨，刘艳萍，高美卿.永磁同步电动机矢量控制［J］.电机与控制应用，2010，37(12):52-55.

［5］KWANG-WOON LEE，SANG BIN LEE.MTPA operating point tracking control scheme for vector controlled PMSM drives［A］.Power Electronics Electrical Drives Automation and Motion(SPEEDAM)，2010:24-28.

［6］裘君，赵光宙，齐冬莲.基于反馈耗散方法的永磁同步电机最大转矩/电流控制［J］.煤炭学报，2009，34(9):1285-1290.

［7］吉智，何凤有.凸极永磁同步电机电流控制方法研究［J］.电气传动，2011，41(7):2-7.

［8］郎宝华，刘卫国，贺虎成，等.基于最大转矩电流比动态磁链给定的直接转矩控制［J］.电气传动，2008，38(1):24-26.

［9］黄鹏，苗长云，黄雷，等.参数在线估算的永磁同步电机最大转矩电流比控制［J］.煤炭学报，2011，36(1):172-176.

［10］田以涛，王英.基于最大转矩电流比的永磁同步电动机矢量控制［J］.电机与控制应用，2013，40(5):25-28.

［11］基于MATLAB的永磁同步电机矢量控制系统［J］.上海电力学院学报，2013，29(3):213-217.

［12］袁喻华，王莉.永磁同步电机矢量控制MATLAB仿真研究［J］.变频器世界，2011(4):68-72.