微车FR型传动系扭振中的驱动轴优化

康 强，何森东，李洪亮，吴昱东

(1.上汽通用五菱股份有限公司，广西 柳州 545007，2中国汽车技术研究中心，天津 300300;3.西南交通大学 振动噪声研究所，四川 成都 610031)*

0 引言

随着人民生活水平提高以及汽车工业的发展，汽车NVH问题研究已经成为当前的热点，其中，动力传动系统扭振是造成汽车NVH问题的重要因素之一［1-2］.针对此类问题的治理措施有很多种，按照治理目标可以分为对振动源的治理、对振动传递路径的治理以及对噪声及振动接收对象的保护.驱动轴为动力传动系扭振传递路径的主要部件之一，对其进行合理的匹配优化，可有效调整传动系的扭振固有特性，避免共振的产生.

本文针对某FR微车由动力传动系扭振引致的低速车内噪声与振动问题，建立了该车动力传动系的扭振当量计算模型［3-4］，通过扭振当量模型分析了驱动轴的结构及刚度对传动系扭振固有特性的影响，实现驱动轴的匹配设计，并最终从计算分析及测试分析对驱动轴的优化后效果进行了验证.

1 问题描述

某FR微车，由于动力传动系在发动机低转速时(转速在1 000～1 500 r/m之间)扭振剧烈，引起车内较大的噪声与振动(车内振动与噪声测试结果如图1所示)，严重影响车辆的乘坐舒适性.

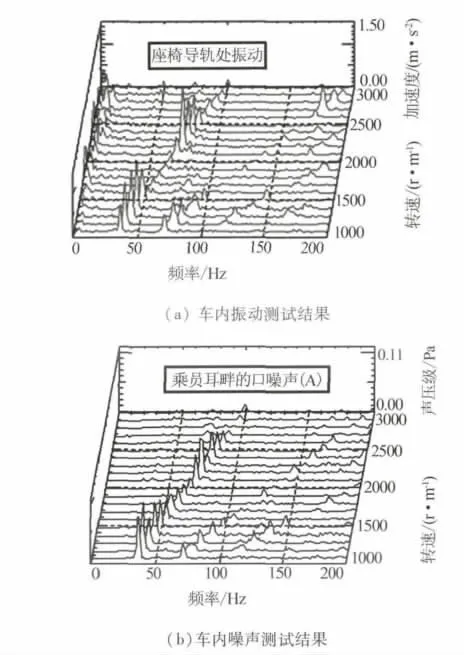
对其动力传动系进行扭振测试后发现［5-6］，该车在发动机低转速时，动力传动系扭振非常剧烈，且在1 100、1 500 r/m附近存在峰值.

图2为动力传动系扭振测试结果，从图中可以看出，该车动力传动系在发动机低转速时扭振较大，并造成了严重的车内噪声与振动问题，必须对其进行治理.

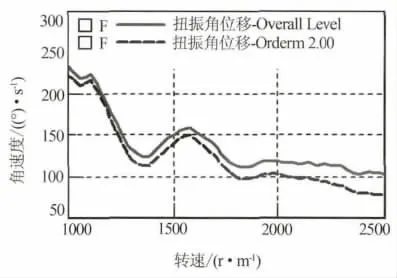
图2 动力传动系扭振测试结果

2 驱动半轴刚度对传动系扭振频率影响分析

2.1 扭振模态数学模型

根据传动系统的力学模型，由达朗贝尔原理，利用拉格朗日方程，建立动力传动系n个集中质量的运动方程，其矩阵形式为:

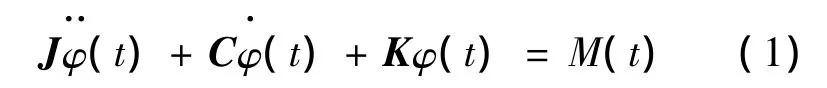
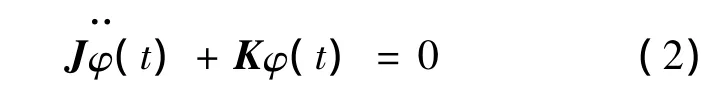
此即无阻尼固有振动的特征方程.系统的第j阶固有频率λj和特征向量φj满足实模态线性广义特征值方程:

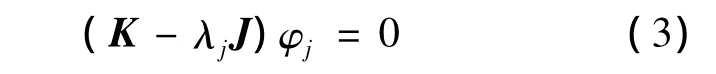
由式(3)可解得系统的固频率λj和相应的实模态振型 φj.

2.2 动力传动系扭振当量模型建立

由于汽车动力传动系统是一个非常复杂的多体系统，为重点分析汽车传动系统的扭转振动，在进行计算分析时，将其实际结构转换成一个由有刚度无转动惯量的轴段以及有转动惯量无刚度的惯量盘构成的多自由度系统，即实际传动系的扭振当量系统.

根据该FR微车的动力传动系及其将使用的双质量飞轮的初设参数，如图3所示建立该车动力传动系的扭振当量计算模型.通过该模型，可以计算获取动力传动系的扭振模态信息以及在发动机激励下动力传动系的扭振响应.

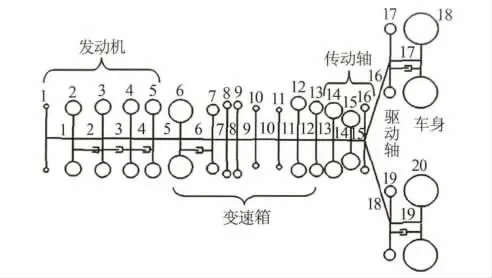
图3 动力传动系扭振当量模型结构示意图

2.3 动力传动系各档位自由振动计算结果

本文主要应用动力传动系扭振当量计算模型，及时各档位下传动系自由振动扭振模态频率如表1.

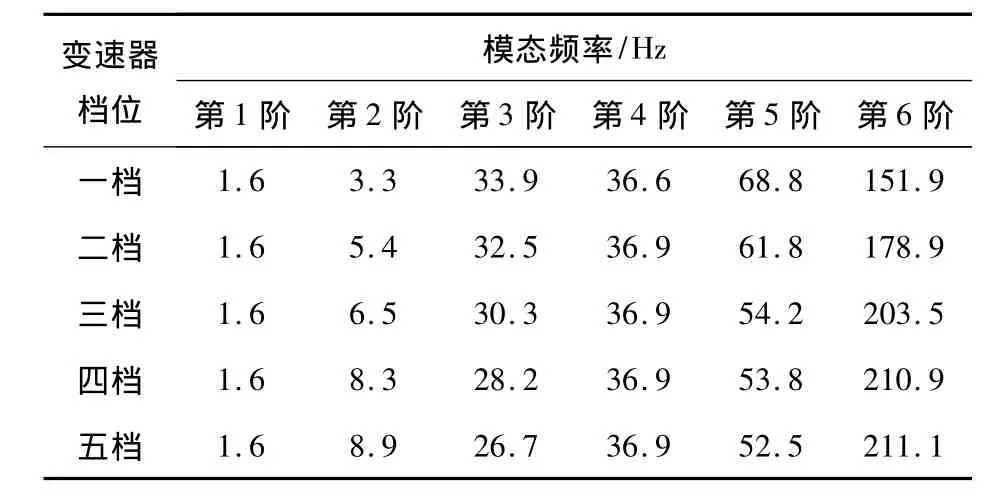
表1 动力传动系扭振模态频率

由动力传动系扭振当量模型自由振动计算结果可以看出:所有档位都存在一个频率为37 Hz左右的扭振模态(第4阶);针对第5阶模态频率，1 档为68.8 Hz，2 档为61.8 Hz，3、4、5 档都在50 Hz附近.这两阶扭振模态最容易在关注转速(发动机1000～1500 r/m)内被激发，而引起车内的噪声与振动问题.

2.4 驱动半轴刚度与动力传动系扭振模态频率计算

为使第4阶模态频率尽量远离敏感频段，可对驱动半轴的刚度进行增强或减弱.利用动力传动系扭振当量模型进行计算，得到动力传动系第4阶、第5阶扭振模态频率随驱动半轴刚度的变化如图4所示，为清晰显示，图中只显示3、4、5档扭振模态变化，其中第4阶模态3、4、5档频率相同为同一曲线.

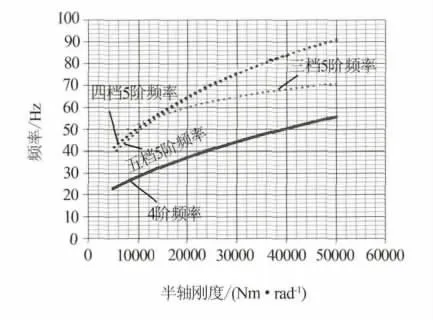
图4 各档位4、5阶扭振模态频率随半轴扭振刚度变化曲线

由计算结果可见:各档位下4、5阶扭振模态频率与半轴刚度成正比，特别5档第5阶对半轴刚度变化尤其敏感.

2.5 动力传动系扭振模态频率与驱动半轴结构尺寸的关系

由于驱动半轴的长度由轮距决定，其长度变化范围极其有限，故主要通过轴径、截面形状的设计来改变其扭转刚度.具体设计方案分为两种，一种是使用实心轴，通过轴径的设计来改变其扭转刚度;另一种是空心轴管，通过轴管内外径设计来改变半轴扭转刚度.

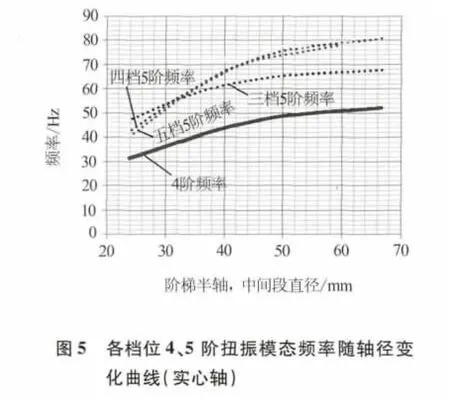
实心轴直径变化各档位4、5阶扭振模态频率变化如图5所示.随着直径增加，模态频率也不断增高.图中只显示3、4、5档扭振模态变化，其中第4阶模态3、4、5档频率相同为同一曲线.

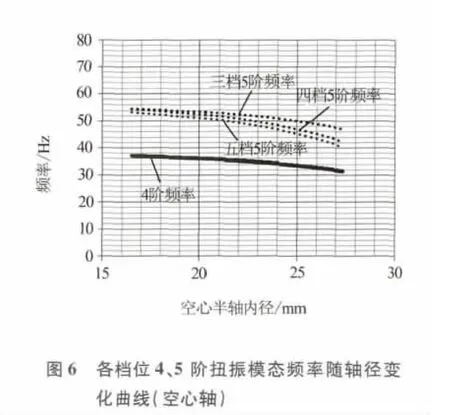
空心轴管内径变化各档位4、5阶扭振模态变化如图6所示(轴管外径31 mm)，随空心半轴内径增加，其模态频率不断降低.图中只显示3、4、5档扭振模态变化，其中第4阶模态3、4、5档频率相同为同一曲线.

3 驱动轴优化方案减振效果

3.1 基于扭振当量模型的计算对比分析

综合以上分析结果，结合工程应用环境，对驱动轴刚度进行调整，主要为增加刚度及降低刚度两个方向，并代入当量模型中进行扭振自由振动及强迫振动计算分析，并将其分析结果与原车状态进行对比.

从表2中可以看出，增加扭转刚度方案，刚度提高33%，第4、5阶模态频率提高4～5 Hz.降低扭振刚度方案，刚度降低约33%，第4阶模态频率降低3 Hz、第5阶模态频率降低4～8 Hz.

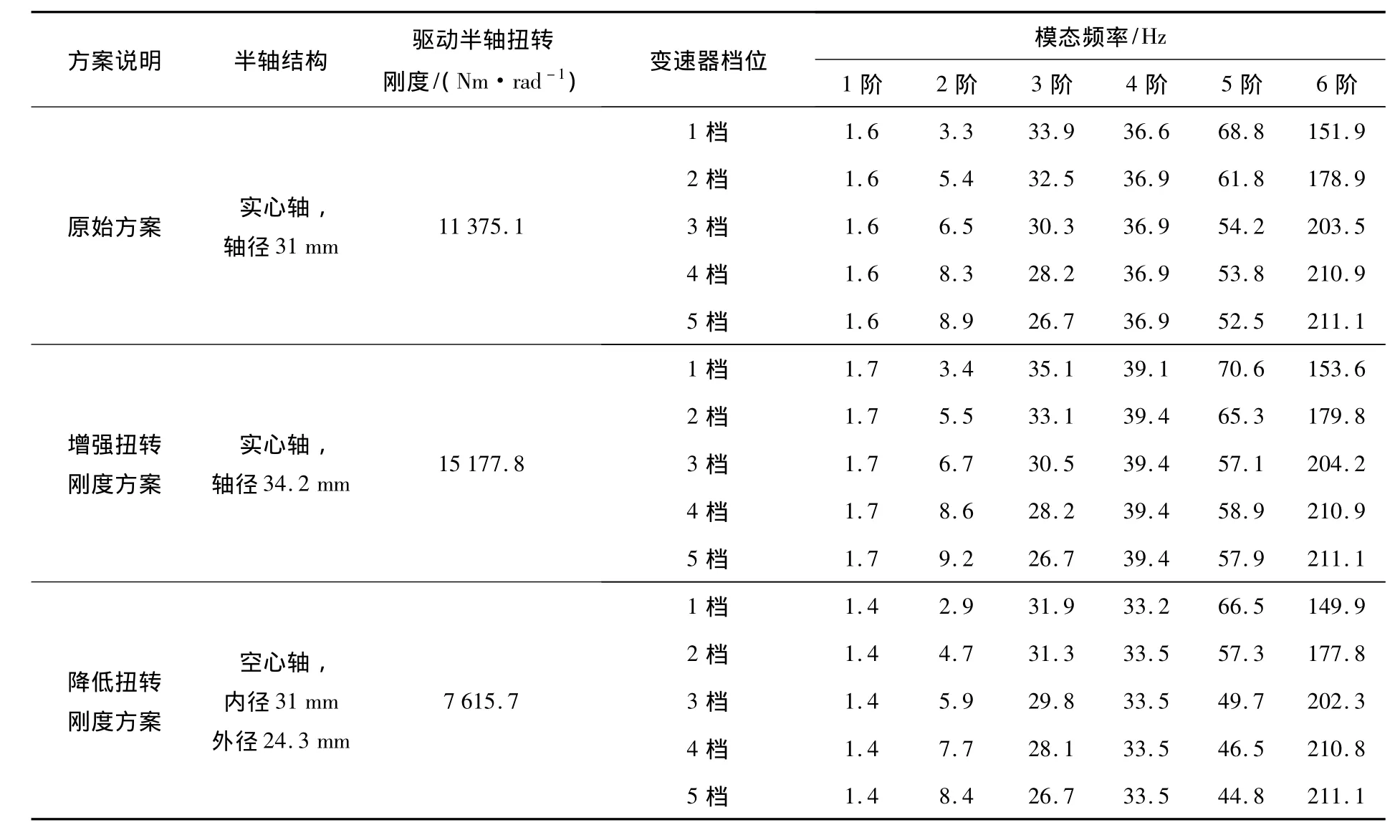
表2 扭振模态频率计算结果

3.2 车内噪声与振动测试对比分析

根据驱动轴设计参数进行试制安装，并对驱动轴刚度增加与降低前后车内的噪声与振动进行测试对比分析.以3档全油门加速工况测试结果进行对比，其余各档位测试结果与此类似.

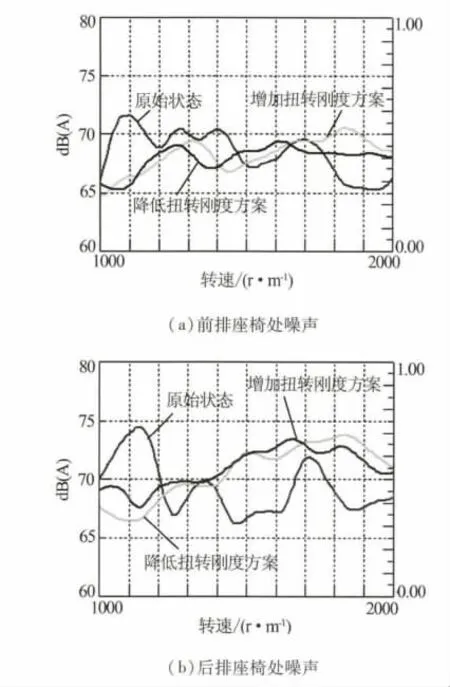
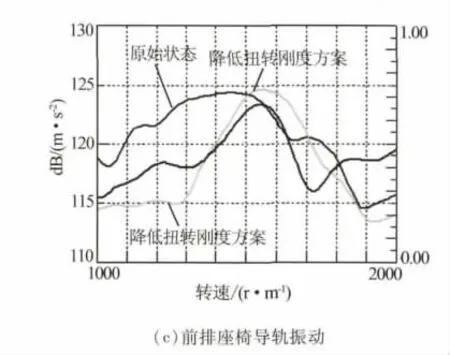
图7 车内噪声与振动测试对比

由图7可以看出，应用驱动轴调整方案后，无论其扭转刚度增大或降低，车内噪声峰值1100 r/m左右均可有效降低6 dB(A)左右，车内振动在1000～1 500 r/m区间也有较大的降低.1 500 r/m左右峰值，车内前排座椅处噪声降低3～4 dB(A)，但后排座椅处噪声有所增大，分析可能原因为第5阶扭振模态变化后与后部车身局部模态引起共振.总体来说与原车状态相比，增大或降低驱动轴扭转刚度，车内噪声与振动随转速变化相对平缓，整车NVH性能有极大的提升，考虑轴系结构强度问题，最终采用轴管增大方案.

4 结论

(1)基于动力传动系扭振当量计算模型，分析了驱动轴扭转刚度及结构设计对传动系扭转频率的影响，为驱动轴与整车匹配的工程设计应用提供了参考;

(2)提出了对驱动轴优化进行轴系扭振控制的方法，首先明确问题原因，然后建立动力传动系扭振当量模型，运用CAE手段进行驱动轴的匹配分析，确定其设计参数，最后进行试制与实车的效果验证.

［1］韩兵，蔡忆昔，张彤.功率分流混合动力传动系统扭转振动分析与刚度匹配［J］.农业机械学报，2011(6):12-15.

［2］周林，郑四发，连小珉.加速工况下传动系统扭转振动分析［J］.振动工程学报，2010(6):601-605.

［3］张代胜，王浩.基于灵敏度分析的汽车动力传动系扭振特性优化［J］.中国机械工程，2013(5):685-689.

［4］许在文，万海桥，黄东东等.汽车传动系扭转振动建模与仿真分析［J］.合肥工业大学学报，2012，35(1):13-16.

［5］章春军.汽车传动系统扭转振动研究与实验［D］.成都:西南交通大学，2011.

［6］MILES T J，LUCAS M，HALLIWELL N A，et al.Torsional and bending vibration measurement on rotors using laser technology［J］.Journal of Sound and Vibration.1999，226(3):441-467.