基于SD的食用油料生产流通多级库存管理模式研究
王明葆,杜志平
(北京物资学院,北京 101149)
1 引言
食用油是大众日常消费品,随着中国居民收入和生活水平的提高,小包装食用油已经逐渐替代散装油广泛出现在各大超市供居民选购,从而极大地扩展了市场。食用油行业更是一个竞争激烈的行业,库存的优化对提升供应链整体竞争力很有作用。食用油料的供应链具有:层级多信息不对称、油料运输方式不同造成各级延迟现象明显、生产企业在供应链中话语权大、具有日常消费品的功能等特点,所以运用系统动力学研究食用油料供应链很有意义。
经查阅相关文献发现,王其藩教授[1]详细阐述了系统动力学建模的方法,并用SD建立了库存劳动力模型、多阶库存模型,在中国开创了SD在多阶库存研究领域的先河。Barlas[2]等人用系统动力学的方法构建了完整的SD模型,研究了服装制成品的生产与库存策略,并依据行业特点给出了政策性建议。Angerhofer[3]从方法论的角度系统性的研究了如何用系统动力学模型来研究供应链管理问题。刘秋生、蒋国耀[4]用系统动力学模型直观的研究了牛鞭效应,分别建立了两阶、三阶、四阶的供应链模型,通过相同情况下仿真结果的比较,证明了供应链长度越长牛鞭效应会越明显。陈文佳、穆东[5]用系统动力学研究了配送中心仓储系统,建立了以配送中心为起点向三个下游店铺配送的系统动力学方程,经过仿真分析发现,减少供货延迟时间、增加需求预测准确性、增加信息交流等方式可以提高系统效率,也体现出了系统动力学在研究供应链库存问题时简洁直观的优势。苗兴东[6]从库存、选址等角度用系统动力学模型研究了供应链管理模式,系统性的介绍了系统动力学在供应链管理领域的应用情况,并用vensim软件建立了模型,在库存领域应用方面论证了可行性。张力菠、韩玉启等[7]对用系统动力学研究供应链管理问题进行了全面的概述,提出了用系统动力学深入研究供应链管理问题应该关注的方向。张力菠、韩玉启、陈杰[8]研究了基于数量的供应商管理库存整合补货的牛鞭效应与成本,利用SD构建了该模式的动态仿真模型,通过仿真结果分析,定量研究了供应商对随机需求输入的订单响应率波动及系统成本的变化趋势,并通过统计学方法分析了牛鞭效应与系统成本之间的数学关系。廖诺、张毕西、吴小节[9]研究了在不同需求条件下供应链系统动态仿真的比较研究,建立了供应链的系统动力学模型。通过使用Vensim对模型进行仿真,对比分析了四种不同需求对供应链系统动态性的影响,仿真结果表明,斜坡和正弦波动两种需求具有渐变趋势的性质,会使供应链各节点的牛鞭效应较小,阶跃需求和脉冲波动需求具有突变趋势的性质,会使供应链的牛鞭效应较大,所以应格外重视这两种需求。赖新峰、陈志祥[10]用系统动力学方法研究了营销策略对生产与库存决策的影响,用Vensim软件建立了三个模型,而且将不同策略的选择和竞争对手引入模型,对于供应链库存决策的研究提供了很好的思路。万振,李昌兵[11]用系统动力学方法研究了闭环供应链中的牛鞭效应,使得供应链库存管理的思路有了很大的拓展,很好的展示了系统动力学对于反馈性的描述。程丽娟、马斌、武毓涵[12]用系统动力学的快速消费品供应链的信息共享问题,发现了信息共享可以有效降低快消品供应链上各个企业的库存波动。
本文在前人研究的基础上,将供应链库存管理模式应用到食用油料供应链,用系统动力学方法着重分析食用油多级库存的影响因素,并将不同模式进行比较,最终在仿真结果的基础上提出优化建议。
2 系统动力学模型的建立
2.1 系统动力学模型假设及系统边界
经调研山东某企业得知,食用油企业的供应链构成一般分三到四级。从生产企业开始、分销商、批发商、零售商逐级向下,最后是终端零售商面对消费者。食用油企业传统供应链是以单一企业为对象去考虑问题的,各个节点企业各自管理本企业的库存,供应链上下游之间信息闭塞,库存信息互不畅通。相比之下供应商管理库存模式由于供应商与下游共享信息,食用油生产商可以直接得到各层级的库存及订货信息,不用再逐级预测和上报。大大减少了信息的延迟和信息的不对称。
在现有传统模式下的食用油料供应链建模假设包括:
(1)供应链系统包括生产商、大区级分销商、市级批发商、零售商四个节点,每一级上游供应商依据下游企业的信息来进行生产和发货,信息逐级向上传递。
(2)根据实际情况知道,生产和发货以及信息的传递是存在延迟的,为了模型的准确性,将生产延迟和各级的延迟时间考虑进了系统动力学模型。
(3)现实中,食用油供应链是由最下游的销售驱动,并逐级传递的,各级存在着销售的预测,故而将各级销售预测考虑进模型。
传统模式下食用油行业供应链系统边界:
(1)食用油生产企业模块:食用油生产企业库存、食用油生产企业销售预测、食用油生产企业期望库存、生产计划单、生产速率、生产延迟、生产商发货速率。
(2)大区级分销商模块:大区级分销商库存、大区级分销商订单、大区级分销商期望库存、大区级分销商销售预测、分销商发货速率。
(3)市级批发商模块:市级批发商库存、市级批发商期望库存、市级批发商销售预测、批发商订单、批发商发货速率。
(4)零售商模块:零售商库存、零售商订单、零售商销售预测、零售商期望库存、零售商销售率、平均销售时间。
(5)其他:延迟时间、VMI策略控制、库存调节时间、库存覆盖时间。
为了直观展现不同模式对食用油行业供应链管理的效果,本文中VMI模式下的供应链管理在模型构建中与传统模式的模型假设和边界相同,通过VMI模式控制这一辅助变量进行控制。
2.2 系统动力学模型影响因素分析
模型中各变量的类型、定义见表1。

表1 变量类型、定义
相应参数的方程如下:
(1)INITIAL Time=0;
(2)FINAL Time=52;
(3)TIME STEP=0.125;
(4)食用油生产企业库存=INTEG[IF THEN ELSE(食用油生产企业库存>=0,生产速率-生产商发货速率,0),8 000],单位:Units;
(5)大区级分销商库存=INTEG(生产商发货速率-分销商发货速率,3 000),单位:Units;
(6)市级批发商库存=INTEG(分销商发货速率-批发商发货率,1 000),单位:Units;
(7)零售商库存=INTEG(批发商发货率-零售商销售率,100),单位:Units;
(8)生产速率=DELAY1(生产计划单,生产延迟)+生产商发货速率,单位:Units/week;
(9)生产商发货速率=DELAY1(大区级分销商订单,延迟时间),单位:Units/week;
(10)分销商发货速率=DELAY1(市级批发商订单,延迟时间),单位:Units/week;
(11)批发商发货速率=DELAY1(零售商订单,延迟时间),单位:Units/week;
(12)零售商销售率=WITH LOOK;UP(Time,([(0,0)-(20,800)],(1,300),(2,500),(3,600),(4,532),(5,446),(6,387),(7,620),(8,334),(9,567),(10,540),(11,478),(12,550))),单位:Units/week;
(13)延迟时间=4,单位:week;
(14)VMI策略控制=0;
(15)生产延迟=0.1;
(16)食用油生产企业期望库存=库存覆盖时间×食用油生产企业销售预测,单位:Units;
(17)食用油生产企业销售预测=SMOOTH(大区级分销商订单,平均销售时间),单位:Unit/Week;
(18)大区级分销商期望库存=大区级分销商销售预测×库存覆盖时间,单位:Units;
(19)库存覆盖时间=5,单位:Units;
(20)大区级分销商订单=IF THEN ELSE(VMI策略控制=0,(大区级分销商销售预测+(大区级分销商期望库存-大区级分销商库存)/库存调节时间),(零售商销售率+(零售商期望库存×3-零售商库存-市级批发商库存-大区级分销商库存)/库存调节时间)),单位:Units/week;
(21)大区级分销商销售预测=SMOOTH(分销商发货速率,平均销售时间),单位:Unit/Week;
(22)市级批发商期望库存=批发商销售预测×库存覆盖时间;单位:Units;
(23)市级批发商订单=IF THEN ELSE(VMI策略控制=0,(批发商销售预测+(市级批发商期望库存-市级批发商库存)/库存调节时间),(零售商销售率+(零售商期望库存*2-零售商库存-市级批发商库存)/库存调节时间)),单位:Units×Week;
(24)零售商订单=IF THEN ELSE(VMI策略控制=0,(零售商销售预测+(零售商期望库存-零售商库存)/库存调节时间),(零售商销售率+0.8×(零售商期望库存×1.5-零售商库存)/库存调节时间)),单位:Units;
(25)库存调节时间=4,单位:week;
(26)批发商销售预测=SMOOTH(批发商发货速率,平均销售时间),单位:Units×Week;
(27)零售商销售预测=SMOOTH(零售商销售率,平均销售时间),单位:Units×Week;
(28)零售商期望库存=零售商销售预测×库存覆盖时间,单位:Units;
(29)平均销售时间=5,单位:week;
(30)生产计划单=IF THEN ELSE(VMI策略控制=0,(食用油生产企业销售预测+(食用油生产企业期望库存-食用油生产企业库存)/库存调节时间),(零售商销售率+(零售商期望库存×4-零售商库存-市级批发商库存-大区级分销商库存-食用油生产企业库存)/库存调节时间)),单位:units/week。
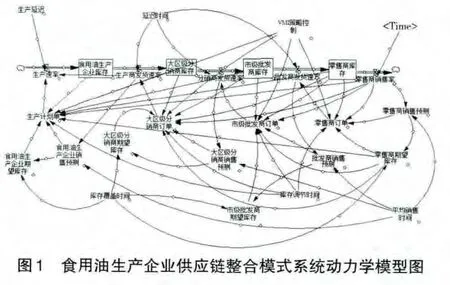
3 模型运行及其仿真分析
3.1 食用油生产流通多级库存模式仿真分析
运用系统动力学软件Vensim ple 5.6a运行上述模型,使用图表功能会得到下面结果,如图2-图5所示。

图2 两种模式下零售商库存的对比


由图2-图5中曲线1可以看出,传统模式下由于信息逐级传递,各种延迟造成了各级企业库存的波动,而且越是处于供应链上游的企业库存量和库存的波动幅度也越大,库存的增大和大幅的波动会造成供应链企业成本的上升,最终给整条供应链造成系统性的风险。
调整VMI策略控制这一辅助变量的值,使得其值为1,这时即启动VMI策略。得到VMI策略实施下的供应链仿真结果,曲线2代表了VMI模式下的仿真结果。
由上面的仿真结果得知,对于食用油行业供应链来讲,VMI模式具有较为明显的优势,在实施VMI策略之后,各级企业的库存均有不同程度的降低,库存的波动也明显减小许多。
3.2 食用油料多级库存影响因素灵敏度分析
控制其他变量的数值不变,观察仅延迟时间变动时供应链上各节点企业库存量的变化。当延迟时间的数值从4周变为3周时,命名为普通模式1,将延迟时间的数值从4周变为5周时,命名为普通模式2。运行vensim仿真,结果如图6-图8所示。
仿真结果显示:延迟时间对于整个供应链的敏感性较强,减少各节点的延迟时间,可以较为显著的降低供应链企业的库存量。所以企业在由普通模式向VMI模式转变的时候,需要首先和供应链其他企业展开信息共享,最好是由供应链核心食用油生产企业推广应用信息共享系统,有效减少信息的延迟,进而减少各节点发货时间的延迟。

图6 延迟时间对批发商库存的影响
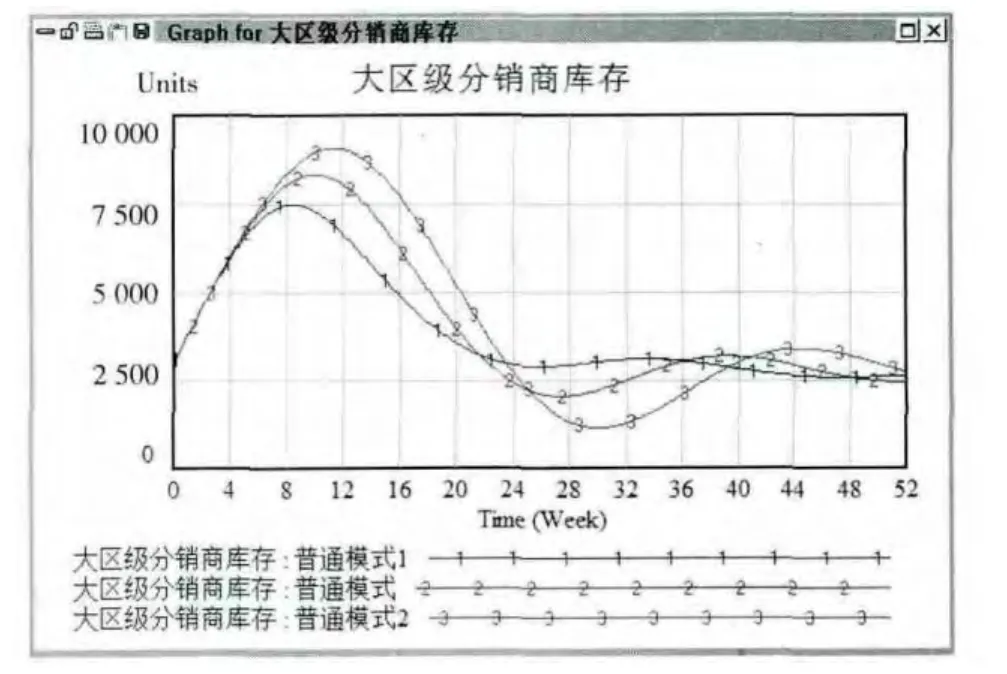
图7 延迟时间对分销商库存的影响

图8 延迟时间对生产企业库存的影响
同理,控制其他变量不变,将库存覆盖时间由4周变为3.5周,将运行程序命名为普通模式3。将库存覆盖时间由4周变为4.5周,将运行程序命名为普通模式4。运行仿真模型得到如下结果,如图9-图12所示。
仿真结果显示:库存覆盖时间对于供应链系统的敏感性也较强,降低各个节点的库存覆盖时间可以有效的降低各节点的库存量,还能有效降低库存波动。所以各节点企业要积极关注库存覆盖时间,加快库存周转,将发货频次和对市场的响应性敏捷性提高,在各企业信息共享和降低延迟的基础上,共同降低库存覆盖时间。

图9 库存覆盖时间对零售商库存的影响

图10 库存覆盖时间对批发商库存的影响

4 结论及政策性建议
根据以上仿真分析,得到以下结论:
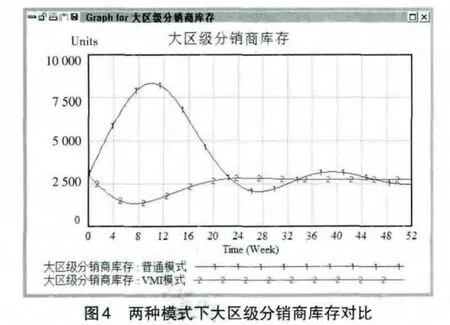
(1)根据对比图发现,实施VMI策略后,各级库存波动幅度明显下降,例如大区级分销商库存从原来的2 000到8 000单位之间浮动变为基本稳定在2 800单位。所以建议食用油企业在条件允许的情况下采用VMI策略来优化供应链库存的管理。

(2)在现有情况下构建VMI模式时,要注意延迟时间对供应链系统的影响,延迟时间的增大会使供应链各个层级的库存波动增强,例如将延迟时间的数值从3周变为5周时,大区级分销商的库存峰值从7 500单位增加到近9 000单位,并且波动幅度显著增大。所以销售信息一定要在整条供应链上通达,尽量减小供应链各个企业之间信息的延迟和不对称。最好建立供应链企业间的信息共享机制和战略合作关系。
(3)各节点企业要积极关注库存覆盖时间,例如将库存覆盖时间从3.5周提高到4.5周时,市级批发商的库存由原来稳定在2 000单位突增到4 500单位,并长期在3 000单位以上波动。所以加快库存周转,依托信息系统和合作模式的构建将发货频次和对市场的响应性敏捷性提高,在各企业信息共享和降低延迟的基础上,共同降低库存覆盖时间。
[1]王其藩.系统动力学[M].上海:上海财经大学出版社,2009.
[2]Barlas Y,Aksogn A.Product diversification and quick response order strategies in supply chain management[R].Working paper,Bogazici University,1997.
[3]Angerhofer B J.System dynamics modeling in supply chain management:research review[A].Proceedings of Simulation Conference[C].2000.
[4]刘秋生,蒋国耀.基于系统动力学的供应链中牛鞭效应的研究[J].中国管理信息化,2009,12(6):72-75.
[5]陈文佳,穆东.基于系统动力学的配送中心仓储系统研究[J].北京交通大学学报(社会科学版),2008,7(1):27-32.
[6]苗兴东.系统动力学在供应链建模中的应用[D].成都:西南交通大学,2006.
[7]张力菠,韩玉启,陈杰,余哲,马义中.供应链管理的系统动力学研究综述[J].系统工程,2005,23(6):8-15.
[8]张力菠,韩玉启,陈杰.基于数量的供应商管理库存整合补货的牛鞭效应与成本研究[J].计算机集成制造系统,2007,13(2).
[9]廖诺,张毕西,吴小节.不同需求条件下供应链系统动态仿真比较研究[J].运筹与管理,2010,19(4).
[10]赖新峰,陈志祥.营销策略对生产与库存决策影响的系统动力学仿真研究[J].中国管理科学,2012,(s2):491-497.
[11]万振,李昌兵.基于系统动力学的闭环供应链中的牛鞭效应[J].计算机集成制造系统,2012,18(5).
[12]程丽娟,马斌,武毓涵.基于系统动力学的快速消费品供应链信息共享研究[J].物流技术,2015,34(1).

