中国物价指数单位根检验中的结构断点问题研究

胡玉筱，胡玉芳，段显明

（1.杭州电子科技大学管理学院，杭州310018；2.河南大学经济学院，河南 开封475000）

0 引言

物价指数是用来衡量通货膨胀的宏观经济指数,具体包括商品零售价格指数（RPI）、居民消费价格指数(CPI)、生产者价格指数(PPI)等不同种类。通货膨胀与总产出等变量的关系一直是宏观经济学的核心问题之一，目前国内也有不少相关的研究。但在对这些关系进行检验时，一个不可回避的问题是，宏观经济变量作为时间序列，有可能是非平稳的单位根过程，这会带来“伪回归”问题。所以，单位根检验成了宏观计量中的常规检验。同时，我国在过去三十余年的改革过程中经历了多次政策变迁，在单位根检验中势必要对结构性变迁或断点加以考虑，才能得出可靠的结论。目前国内的文献对此罕有顾及，往往会导致检验功效降低，这也是宏观计量研究的一个软肋。

本文以1986～2012年的月度消费物价定基指数为对象，研究单位根检验过程中的结构断点问题。该问题在单位根检验的理论探索中取得了一定的成果，被提出的方法也有多种。本文将结合不同方法来确定物价指数中的断点，并在考虑断点的情况下，检验单位根假设是否能被接受。

1 单位根检验

ADF检验是Dickey&Fuller年提出的DF检验方法的基础上进行扩展的。最初的DF检验基于1阶自回归方程，主要考虑了三种不同的情形，即随机游走模型、包含截距项和含有截距项和确定性趋势的数据生成过程。如下：

其中a0，γ，a1为参数，εt是一个服从均值为零、方差为有限常数值的独立分布；原假设为γ=0，通过临界值与t统计量的比较，可以确定序列是否存在单位根，这里的临界值参照的是Dickey&Fuller计算出的给定样本容量条件下的经验近似临界值，特别需要注意的一点是t统计量的临界值与所选取的回归方程的形式有关。

DF检验用在高阶自回归方程中，也就是由AR(1)过程扩展到了AR(P)过程，就是扩展的DF检验，即ADF检验。与方程(3)相应的p阶自回归方程如下：

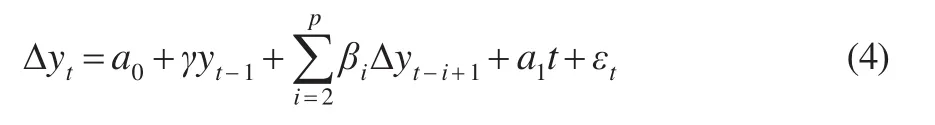
若γ=0，则yt序列接受存在一个单位根的原假设，若γ＜0,则拒绝原假设。这里使用的临界值是Dickey&Fuller（1981）提出的临界值。而滞后阶数p除了通过序列相关性来辅助识别外，还常常采用AIC和SBC两个模型筛选准则来判断。

PP检验是由Phillips与Perron提出的，也是单位根检验常用的方法之一[1]。与ADF检验不同的是序列yt中的随机趋势μt是一个服从无穷阶的MA过程，即：这样随机扰动项就不再服从独立同分布，而是序列相关的，以至于t统计量检验受到相关性的影响，实际分析时，需要通过Newey-West异方差与自相关进行一致估计来调整标准误，从而修正统计检验量。

PP检验方程为：

原假设Η0:β=0.我们根据常规t统计量，从而得到PP检验的t统计量推算式为：

其中，

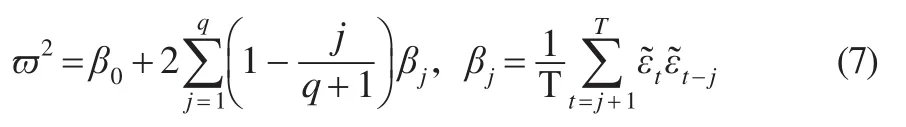
tβ是β系数的t检验统计量，而sβ则是其标准误差，标准误的估计值为σ̂，T为总样本时期，q为截尾期。

而KPSS检验则是从与ADF检验相反的假设设定来进行的。KPSS检验原假设为序列平稳，而备择假设则是序列含有单位根。这对于较低功效的ADF检验来说，起到了补充作用。

2 考虑结构断点的单位根检验

对本文所研究的CPI时序数据采用内生性结构断点检验，即假定结构断点发生时间未知，依据ZA模型思想方法，本文假设所研究的时序数据所有的点都有可能是结构突变点，然后通过ADF循序检验并计算出所有t统计量，从中选出最小t统计量所对应的λ（λ=ΤB/Τ，ΤB为结构断点发生时间）值，从而估计出结构断点发生的日期。原假设为序列不含有结构断点的单位根，备择假设为含有未知结构断点的趋势平稳。建立模型如下：

原假设：

备择假设：

其中，λ=ΤB/Τ，ΤB为所选样本中结构断点发生时间，当t＞Τλ时 ，DUt(λ)=1 ，否 则 为 零 ，当t＞Τλ时 ，DΤ*(λ)=t-Τλ，否则为零。结合ZA（1992）模型所建立的备择假设可以给出下面的直观描述如图1所示：

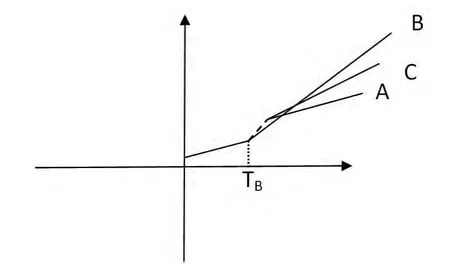
图1 三种断点情形的直观图

文中对于假设检验的判断，是通过计算出检验αi=1(i=A，B，C)的t统计量，然后根据Zivot&Andrews计算出的临界值来选取其最小值，并依据最小t值对应的λ值来推出相应的结构断点时间[2]，用数学式来表示如下：

另外，关于所建模型中的k阶滞后数是由t统计量的显著性来确定的，即先设定一个范围，由较大的滞后阶数开始尝试，当j=k时，Δyt-j的系数的t统计量的绝对值比1.60大，1.60为渐近正态分布在10%显著水平的临界值，这时我们认为滞后阶数为k，当j＞k时，的t统计量的绝对值小于1.60。

3 实证分析

3.1 数据说明与处理

本文采用1986年1月至2012年12月的居民消费价格指数的月度定基指数为研究对象，其中1986年到2000年之前的消费价格指数数据源于卢锋、彭凯翔[3]，在此基础上，又通过国家统计局网站及其他官方资料中搜集到2000年以来的同比消费价格指数和环比消费价格指数，然后利用同比月度数据和环比月底物价指数数据，计算出2000年以来的月度消费价格定基指数数据。

在实证分析时，我们对1986年1月至2012年的时序数据取自然对数，进行无量纲化处理以后，对其做差分表示的是数据的变化率，即通货膨胀率。取对数后的定基物价指数月度数据图示如图2所示。

由图2我们可以看出，由1987年中期开始通货膨胀率急剧上升，到1989年达到了第一阶段的峰值；随着新一轮经济的增长，1990～1993年初期间，通货膨胀率基本上处于相对平稳的持续波动中，而1993年初开始，通货膨胀率出现了急剧上涨，1994年通胀率达到了数年来的最高水平。这一波严重的通货膨胀现象最终并没有恢复到以前的低通胀水平，而是在国家采取紧缩的货币或财政政策下持续振荡，随后从1998～2004年这一期间，从图中可以看到，通货膨胀率有稍微的下降趋势，而这一现象正与当时所公认的通货紧缩现象相一致。但2004年以后，特别是在2005年通货膨胀率又出现了上扬的趋势，显现了新一轮通货膨胀的征兆，这与2007年的通货膨胀相照应，2008年达到了膨胀率更为严重的水平。

通过对去自然对数后的消费价格指数数据的观察，以及从该时序数据的自相关分析图中也可以看到ACF系数是缓慢衰减的并趋于0，这正好与该价格指数数据的逐渐上升的趋势保持一致。说明该消费价格指数时序数据是非平稳的。而1988年到1989年及1993年到1994年的急剧上升，很明显受到了外界因素的冲击，所以不能排除该时序数据含有结构突变的可性[4]。

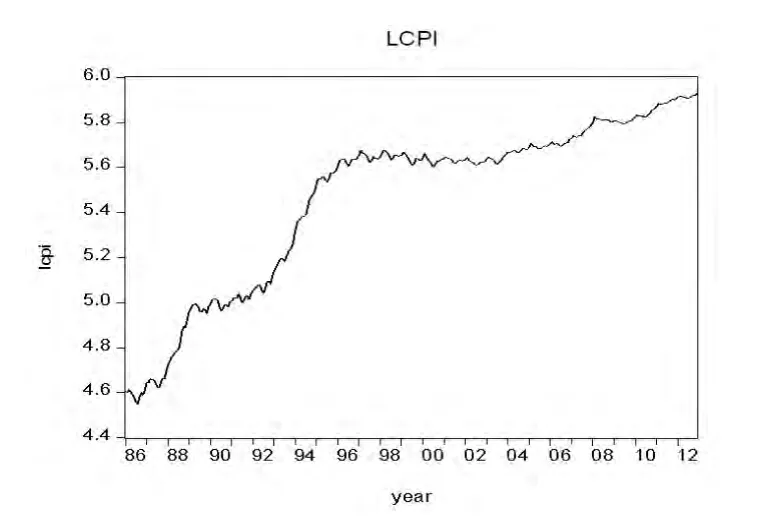
图2 居民消费价格定基指数取对数月度数据（1986年1月-2012年12月）

另外，我们从图2还可以发现，在时序数据的长期动态过程中，趋势线上有很多锯齿状的波动。而对于大多数月度或季度经济变量都会受到季节因素影响的时序序列，因此，在对消费价格定基指数月度数据进行非平稳检验和依据ZA模型进行内生性结构断点的单位根检验时，本文首先基于EVIEWS6.0运用TRAMO/SEATS方法对CPI时序数据进行了季节调整。调整后的时序数据为lcpisa（如图3），很显然，与图2相比较而言，调整后的序列更加平滑。

图3 季节调整后的价格定基指数

3.2 单位根检验

首先对调整后的数据变量进行ADF单位根检验，通过序列相关性我们看到lcpisa序列在水平上自相关图是逐渐衰减过程，而偏自相关图则是一阶截尾的，所以可以初步判定该序列属于非平稳的。因为本文所研究的数据样本数为324个，远远大于100个样本点，故在本文的单位根检验中是依据SBC来确定模型的滞后阶数。

由于在ADF检验中可根据序列本身的性质，检验方程分为三种形式，即包含常数项，包含趋势和常数项或者两者都不包含。依次按照这三种方程形式进行单位根检验，需要强调的是，常规t检验统计量不再适用，这里采用的是Divot&Andrews（1981）算出的临界值分布。

用处理后的消费价格指数数据的一阶差分作为因变量分别依据ADF检验的三种形式做回归，其中，原假设为该序列存在单位根，即lcpisat-1系数为0。在表1的检验结果中可以看出，对序列进行ADF单位根检验，在三种情形下都一致不能拒绝单位根原假设。

与ADF单位根检验一样，依次按照三种检验类型分别进行PP检验和KPSS单位根检验。在PP检验中，q截尾期由EVIEWS6.0中的软件系统根据所验证的序列样本数量自动选取。而KPSS检验与其他单位根检验方法所不同的一点在于它的原假设是设定序列为（趋势）平稳。表1中的t（lcpisa）是基于原序列进行单位根检验的t统计量，而t（dlcpisa）则是基于序列一阶差分检验得出的t统计值。

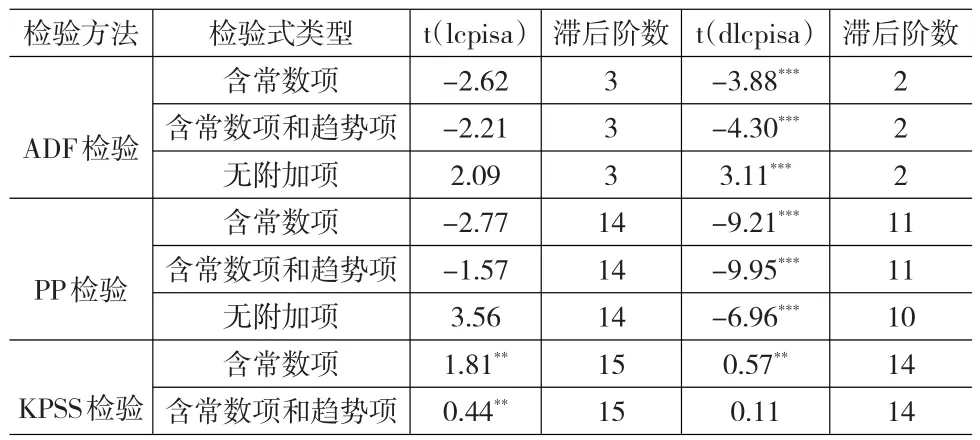
表1 ADF、PP、KPSS单位根检验结果

通过上述ADF检验、PP检验和具有相反原假设设置的KPSS非参数检验，我们发现，对于lcpisa进行level的检验，这三种检验方法所得出的结果是一致的，即认为消费物价定基指数时序数据是非平稳的。但对于lcpisa进行KPSS一阶差分检验时，当检验式含有截距项，该检验拒绝平稳性原假设；而含有截距项和趋势项时，该检验接受原假设。ADF检验和PP检验对于序列的一阶差分单位根检验都是拒绝单位根原假设的。得出这样的结论，就需要去考虑序列中是否存在结构断点，去验证是否把含有结构断点的趋势平稳误判为单位根过程。

3.3 考虑结构断点的单位根检验

为了进一步确定通货膨胀长期波动结构特征，运用ZA模型方法进行内生性结构断点单位根检验。对上述的(9)～(11)式方程进行变形，即得到如下方程：

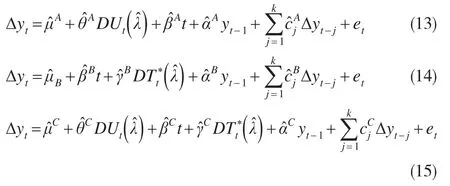
在该模型检验中，原假设为：̂=0；备择假设为：＜0.使用Eviews6.0软件，在workfile窗口创建一个program，用命令程序实现对内生性结构断点的单位根检验，结果如表2所示。

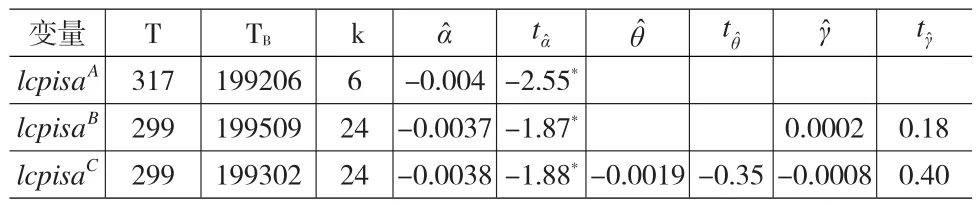
表2 采用ZA(1992)模型A、B和C对lcpisa序列的检验结果

通过A、B、C三个模型中的t统计量时序数据，可以发现三模型分别对应最小的t统计检验量为-4.479、-3.5762、-4.950。而这三个最小的t统计检验量对应的日期分别是1992年6月、1995年9月和1993年2月。而且从表3可以发现，最小t统计量所对应的日期与其他次小t统计量所对应的日期相差并不很大，所以可以初步推断三种情况下的断点日期分别大致发生在1992年、1995年和1993年。而1992年至1995年期间，我国恰处于一波经济增长、通货膨胀严重的阶段。

关于模型A、B、C检验结果的线型图4、5、6所示。模型A、C在10%的显著水平下，序列拒绝接受原假设。结合第二部分所述的经济背景，我们知道，1993年是价格制度深入改革的一年，并且1993年取消了粮食统销的管制政策。由图3，我们可以判断在1993年存在一个较为显著的斜率上的断点，但由于模型C中滞后的阶数是24阶，所以1986年和1987年的数据就被去掉了，这样就导致90年代初的斜率断点显著性有所下降。另外，模型A检验结果中显示其最大对数似然值为1268.6，而模型C的最大对数似然值为1216.1。所以由于模型C选取的滞后阶数较大，使模型A显得较为符合数据的潜在生成过程。

由于断点的形式、个数与确定性趋势的形式均未知，ZA检验的假设仍然太强了，而在基于状态空间的结构时间序列模型里可以不用预先做这些假设。

表3 最小t统计量

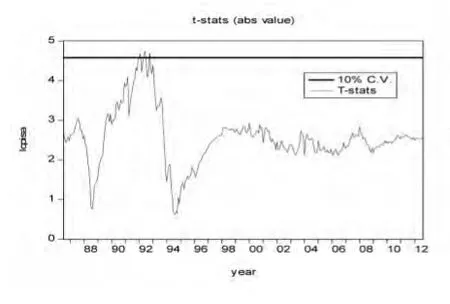
图4 Model A检验结果

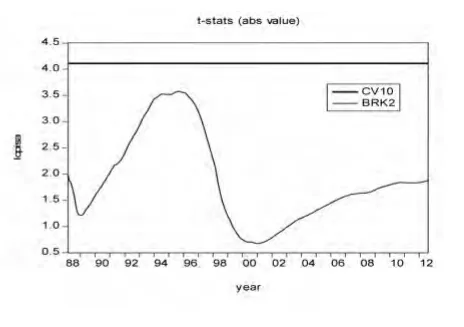
图5 Model B检验结果

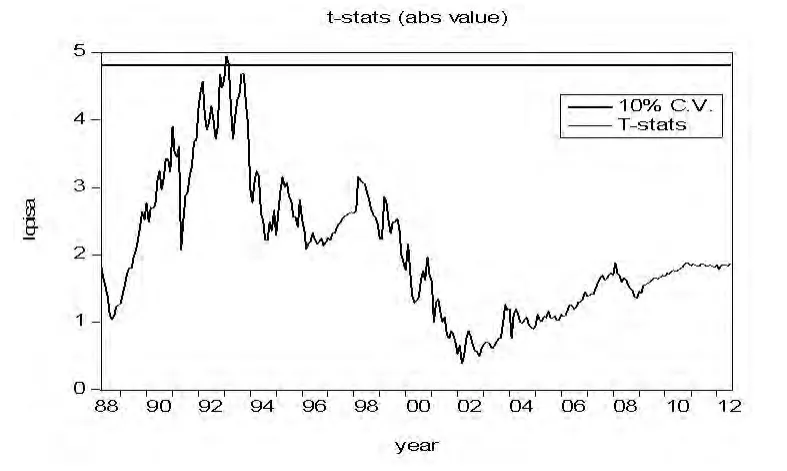
图6 Model C检验结果

4 结论

通过以上各种方法对通货膨胀序列进行检验得出了不尽一致的结果。在不考虑结构断点的存在，而仅单纯进行单位根检验时，ADF、PP和KPSS检验方法得出了不同的结论，对于含有截距项的一阶差分检验式进行KPSS检验结果显示其是非平稳的。故对于序列的单位根检验时，考虑结构断点的存在是很有必要的。ZA模型认为截距上的断点发生在1992年6月；斜率上的断点在1995年9月，此种情形并不显著；而趋势和斜率都发生断点日期为1993年2月。

1994年1月我国进行了汇率并轨改革[5]，同时1994年的严重通货膨胀与1993年的粮食统销政策的取消也是有关系的，这也说明了在状态空间模型中斜率断点日期为1993年5月，截距上的断点发生在1994年1月，这两个断点相差并不大，同时也对应了ZA模型C得出的断点日期是1993年2月。故同时包含截距和斜率上的断点日期发生在1993年，这与当时的经济背景也是相对应的。

结构断点的产生与外部政策、事件等冲击是密切相关的，且对于确定序列的数据生成过程，进行单位根检验时考虑结构断点的存在是很有必要的。而要更进一步的确定断点的稳健性，还需要把初步判断出的断点带回去重新进行检验，这有待对其进行更深一步的探索。

[1]Perron P.The Great Crash,The Oil-Price Shock and The Unit-Root Hypothesis[J].Econometric,1989，(57).

[2]Zivot,E.&D.Andrews.Further Evidence on The Great Crash,The Oil-Price Shock and The Unit-Root Hypothesis[J].Journal of Business and Economic Statistics,1992,(10).

[3]卢锋,彭凯翔.中国粮价与通货膨胀关系（1987-1999）[J].经济学(季刊）,2002,1(4).

[4]贺凤羊,刘建平.金融危机前后我国CPI涨跌的路径分析——基于结构突变理论的实证研究[J].产经理论,2010,1(1).

[5]王少平,李子奈.结构突变与人民币汇率的经验分析[J].世界经济,2003,(8).