基于索洛扩展模型的中国地区工业绿色经济增长核算

杨文举

（重庆工商大学 长江上游经济研究中心，重庆 400072）

0 引言

近年来，国内外一些研究在经济增长核算分析中，尝试性地将环境变量和资源变量与资本、劳动等一起纳入了基于索洛扩展型的经济增长框架。这种绿色经济增长核算研究不仅有助于更加真实地识别经济增长的源泉，而且还有助于经济发展中的相关决策制定，特别是对我国当前及今后在转变经济发展方式中的路径选择具有极大的现实意义。

基于索洛扩展模型的绿色经济增长核算研究，以早期基于索洛模型的新古典经济增长核算模型为基础，将环境变量作为一种投入成本（它们代表经济活动对环境资源的消耗）引入总量生产函数，进而将经济增长的源泉分解为全要素生产率变化（索洛余值）和各种投入增加（包括劳动力、资本、环境、中间投入品或能源、土地等）等源泉。迄今为止，国内外已有一些研究从以下两大思路出发对这种基于索洛扩展模型的绿色经济增长核算进行了尝试性的经验研究。一是从修正传统的产出变量出发，将环境变量等引入新古典经济增长核算分析框架的绿色经济增长核算研究。二是将各种环境破坏视为投入变量并引入新古典总量生产函数，并据此来进行的绿色经济增长核算研究。

现有的两组新古典分析框架下的绿色经济增长核算研究在处理环境变量方面都做出了极具价值的探讨，这些各具优劣的尝试性研究对于分析中国经济增长的源泉都具有很好的借鉴作用。目前，国内相关研究中不乏存在这两种思路下的经验分析，但是相关研究基本上都是以全国行业发展（包括工业和农业）为分析对象的经验研究，而鲜有研究对中国省份经济或省份行业进行类似的绿色经济增长核算。另外，从“物质平衡原理”角度出发，生产函数中一旦引入原材料等中间投入变量，则产出变量就不应该是增加值而应该是总产值。然而，国内相关研究在引入原材料和环境变量的同时，却未能用总产出而不是增加值来修正总量生产函数。因此，本文从弥补国内既有研究在上述两大方面的缺陷出发，对该领域进行一个补充性研究；同时从经验分析角度进一步验证环境变量对经济增长核算结果的影响。由于第一种思路需要环境变量的影子价格信息，其获取难度较大而且采用不同方法得出的差异性结果还会较大地影响经济增长核算结果。有鉴于此，本文拟采用第二种思路尝试性地将原材料、环境变量、资本、劳动力和总产值同时纳入总量生产函数来构建绿色经济增长核算模型，并对中国大陆省份工业进行经验分析。

1 基于索洛扩展模型的绿色经济增长核算模型

1.1 引入环境变量的索洛增长核算扩展模型

传统的索洛增长核算模型没有将环境变量纳入分析框架，这不利于识别经济增长的真实源泉，从而会影响经济决策的制定。在相关研究中，代表性的环境变量如工业废气中的二氧化硫排放量、工业废水中的化学需氧量、工业废水中的生化需氧量等，所选取的变量都只有其中的1种。本文认为，在数据可得的前提下，尽可能多地引入环境变量有助于更好地反映经济现实情况。在引入原材料的情况下，从“物质平衡原理”出发，总量生产函数中也应选用总产值而非增加值。因此，本文在借鉴相关研究的做法基础上，把工业废气中的二氧化硫排放量（SO2）和工业废水中的化学需氧量排放量（COD）作为代表性的环境变量，与劳动力（L)、资本(K)、中间品度量的原材料(M)和代表技术进步的时间（T）一起作为投入变量，并以地区工业生产总值(GCZ)作为产出变量，构建总量生产函数，见式（1）。

在完全竞争假定下，式（1）中的产出增长可被分解为投入变动的贡献(劳动力、资本和原材料投入）、公共副产品即污染排放的贡献（SO2和COD)和全要素生产率增长的贡献（TFP）3大部分。对式（1）两边取自然对数并对时间T求导，省略脚标t和i，得到式（2）。其中，α、β、γ、δ和λ分别代表资本、劳动力、原材料、SO2和COD的产出弹性系数；g表示增长率；d为求导符号；ln为求自然对数符号；ε为余值，即全要素生产率。

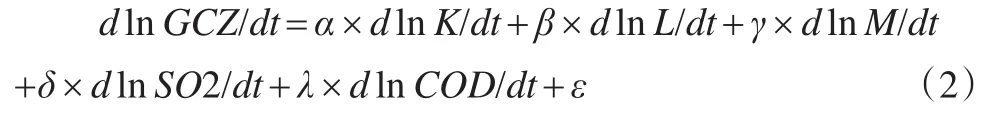
即：

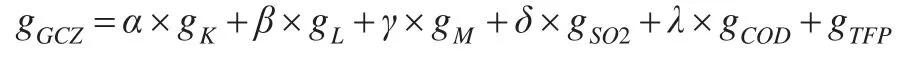
进一步假定生产中服从规模报酬不变，即α+β+γ+δ+λ=1，则式（2）可进一步变形为式（3）。

1.2 产出弹性系数的计量分析模型

为测度式（2）所示的绿色经济增长源泉的相对贡献大小，除了需要各投入、产出变量的相关数据之外，还需要确定α、β、γ、δ和λ5个产出弹性系数。目前，产出弹性系数值的选取主要有3种思路：一是根据各投入要素的报酬占总收入（总产出）的比重来加以确定；二是根据前期相关研究结论给出相应的经验数值；三是通过计量分析模型来确定。由于本文的投入变量中选取了原材料和环境变量，它们的产出弹性系数值难以从前两种思路中获取，因此采用计量分析思路来获取所有投入变量的产出弹性系数值。为此，结合式（3），构建式（4）所示的计量分析模型（各变量省略了脚标i和t）。

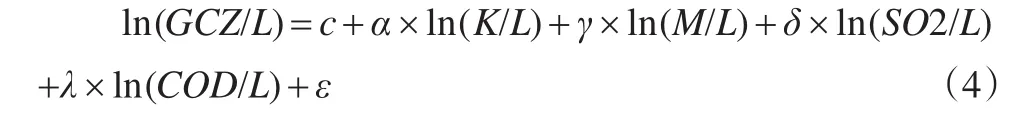
2 中国地区工业绿色经济增长的核算

2.1 变量和样本的选取

根据前述绿色经济增长核算分析框架，为探讨资源、环境双重约束下中国地区工业经济增长源泉的相对贡献，首先需要确定绿色经济增长核算框架下的投入、产出变量。本研究沿袭相关研究的做法，在兼顾数据可得的情况下，选取省份工业生产总值为产出变量(GCZ)，省份工业年均从业人员数作为劳动力投入变量（L)，省份工业固定资产净值年均余额作为资本投入变量(K)，省份工业中间品价值作为原材料投入变量（M)，省份工业废气中的二氧化硫排放量（SO2)和省份工业废水中的化学需氧量（COD)作为代表性的环境变量。其中，工业生产总值、劳动力、工业二氧化硫排放量、工业废水化学需氧量的数据直接来源于中经网、《中国统计年鉴》、《中国环境统计年鉴》；工业中间品价值按照工业总产值与工业增加值之差获得，其中2011年、2012年的工业增加值数据根据当年各省的统计公报相关数据推算得出，其余年份的数值源于《中国统计年鉴》。

在具体的数据选取中，一旦在不同年份公布的统计资料中对同一年份的数据统计存在差异时，本文以近期公布的数据为准。限于部分数据在早期缺乏统计（如二氧化硫排放量、化学需氧量等），本文分析数据的时间跨度选取为2003～2012年，研究对象涵盖大陆31个省市区。所有数据的一般统计描述见表1，其中工业生产总值和固定资产净值年均余额以2000年为基期进行了相应平减，平减指数分别为GDP平减指数和固定资产投资价格指数。

表1的数据表明，所有数据的最大最小值比都在400以上，而且各变量的标准差均接近（部分变量还大于）相应的中间值和平均值，这充分表明中国各省在2003～2012年间的工业发展差异较大。如此巨大的数值差异不仅表明中国各省的工业经济规模和增长速度差异大，而且也表明它们对环境的影响也具有较大差异。因此，为深入探讨中国省份工业经济增长源泉，将污染排放物引入分析模型中是具有至关重要意义的。

表1 中国省份工业投入、产出指标统计描述：2003-2012

2.2 索洛扩展模型的计量分析

以中国大陆除31个省份2003-2012年的面板数据为分析样本，对式（4）进行回归分析。为合理地对回归模型进行选择（混合回归模型、固定效应模型或随机效应模型），先对个体随机效应模型进行估计并作Hausman检验，Hausman值为90.02，其对应的P值为0，拒绝了原假设（应建立随机效应模型），这表明应建立个体固定效应模型。然后在个体固定效应模型的输出结果下进行似然比检验，F值为5.51，对应的P值为0，拒绝原假设（应建立混合效应模型），应建立个体固定效应模型。根据上述检验结果，对式（4）进行个体固定效应回归分析，结果见表2。

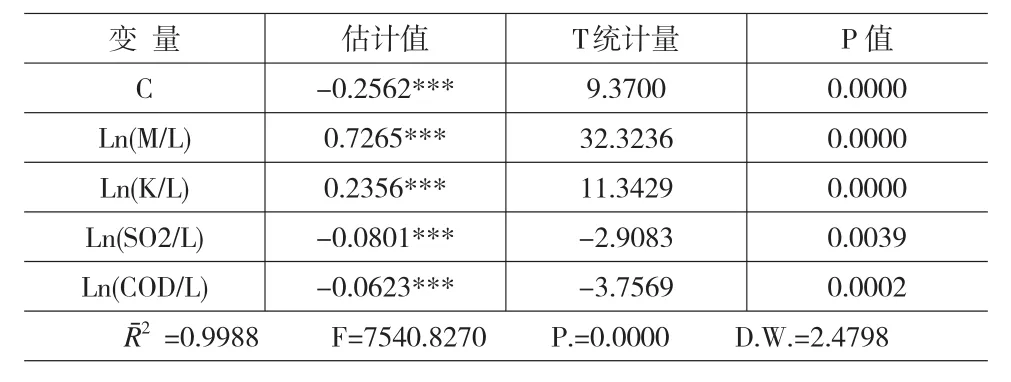
表2 中国省份工业个体固定效应模型回归估计结果

在回归估计结果中，回归方程调整后的可决系数高达0.9988，表明该模型整体上较大程度地揭示了被解释变量的影响因素，拟合优度高；F值远大于临界值，表明随机误差具有同方差性，回归方程显著；D.W.值为2.2289，表明回归估计结果中不存在残差序列相关；而且各解释变量的待估参数值至少在10%的显著性水平上通过了T检验。因此，该模型及回归分析结果具有较好的解释力。

从回归结果分析中Ln(M/L）、Ln(K/L）、Ln(SO2/L）、Ln(COD/L）的参数估计值可以得知，在分析期间内中国省份工业经济增长中原材料、资本、劳动力、SO2和COD对工业总产出的产出弹性值分别为0.7265、0.2356、0.1803、-0.0801和-0.0623。就3个传统的投入变量而言，它们的产出弹性值均为正数，这与相关研究结论一致。比如，Elsadig（2007）对马来西亚制造业1970～2001年间的估计结果表明，中间品、资本、劳动力对工业总产值的产出弹性值分别为0.53、0.14和0.13；罗岚（2012）对中国工业1990-2010年的估计结果中能源、资本和劳动力对工业增加值的产出弹性值分别为0.0290、0.9571和0.2201。而作为环境变量引入的SO2和COD两种投入的产出弹性值都为负数，这与相关研究结论具有一定差异性，如Elsadig（2007）对马来西亚制造业的研究中BOD对工业总产值的产出弹性值为0.20，但罗岚（2012）对中国工业的研究中SO2对工业增加值的产出弹性值为-0.2325。本文认为，从“物质平衡原理”角度而言，这种环境变量（副产出或非期望产出）的产出弹性值为负数时较为合理。因为作为副产出的SO2和COD等污染性排放物，其产生需要消耗掉必要的各种投入资源（包括原材料、劳动力和资本等），在投入给定的前提下，它们的产生量越大，用于生产期望产出的投入资源就越少，从而期望产出增加就越少。

2.3 绿色经济增长核算

结合式（2）和表2的估计结果，运用中国大陆31个省份2003～2012年的面板数据，对各省工业进行绿色经济增长核算，结果见表3。

从表3中显示的核算结果中初步可以得出下述两大结论：

第一，各种投入（含环境投入）对中国工业经济增长的相对贡献率大小具有较大差异，但各省工业经济增长的主要源泉都是原材料和资本投入。其中，原材料、资本和劳动力等投入积累和全要素生产率提升都对经济增长做出了不同程度的贡献，它们对工业总产出增长率的平均贡献率分别为75.81%、16.99%、3.65%和3.69%。而二氧化硫排放和化学需氧量对工业经济增长的贡献率分别为-0.60%和0.47%，这与相关研究结论比较一致，如罗岚（2012）的研究表明，在1990～2010年间工业二氧化硫排放对中国工业增加值增长率的贡献也为负数，其值为-4.84%；化学需氧量对工业经济增长的贡献率为0.12%，笔者认为这也是合理的。之所以我国二氧化硫排放量和化学需氧量对工业经济增长的贡献具有如此大的差异，其原因在于二氧化硫排放量和化学需氧量的产出弹性都为负数，但是在分析期间内它们的年均增长率却分别为1.60%和-1.55%，从而其经济增长贡献率不可避免地出现上述不同取值情况。从绿色全要素生产率提升对工业增长所起到的较大促进作用来看，最近十年来我国各省在工业生产技术和技术效率方面取得了较快进步，它们不但推进了工业期望产出水平的快速提高，而且还对二氧化硫和化学需氧量等工业非期望产出起到了较好的减排作用。

第二，中国省份工业经济增长源泉的相对贡献率具有不同程度的省际差异。其中，原材料和资本投入都无一例外地促进了工业总产出增长，但具有一定的省际差异，其贡献率的标准差分别为4.82%、3.66%，最大最小值比分别为1.2923和3.1924。多数省份（21个）的绿色全要素生产率变化都促进了工业产出增长，省际差异也较大，其贡献率的标准差为6.76%，其中贡献率最大的为青海（27.05%），贡献率最小的为北京（-6.20%）。省份劳动力投入贡献率的省际差异也较大，其标准差3.15%接近其平均值3.65%，而且西藏（-7.91%）、甘肃（-3.03%）2省的劳动力投入减少还阻碍了其工业经济增长，而在劳动力贡献最大的广东省，因劳动力大幅增长而引致的增长在总产出增长中占据了8.78%的比重，其次为江苏（7.34%）。二氧化硫排放量对工业经济增长率的贡献率也具有大的省际差异，标准差为2.25%，其中有21个省份的贡献率小于0，贡献率最大的为北京（4.45%），其次为上海（3.88%），贡献率最小的为新疆（-6.26%），其次为青海（-4.46%）。化学需氧量对工业经济增长率的贡献率也具有大的省际差异，标准差为2.85%，其中有10个省份的贡献率小于0，贡献率最大的为四川（3.88%），其次为山东（3.43%），贡献率最小的为青海（-10.74%），其次为贵州（-4.25%）。

表3 中国省份工业绿色经济增长核算结果（2003-2012）：平均贡献率 （%）

3 与传统增长核算结果的比较

本文在前面指出，忽略环境变量的经济增长核算将影响经济增长核算结果，这无助于识别经济增长的真实源泉，但是相关经验研究结论却未得出一致意见。其中，多数经验研究结论与此一致，如Elsadig（2007）、罗岚（2012）、杨文举（2011；2012）等发现不引入环境变量时的全要素生产率变化要高些，从而会高估其在经济增长中的相对贡献，但是王奇（2012）对中国农业的分析结论却未得出引入环境变量前后的全要素生产率变化会有显著差异的结论。为此，下面先对不引入环境变量的情形进行经验分析，然后与前面的分析结果进行对比，经济增长核算及对比结果见图1。

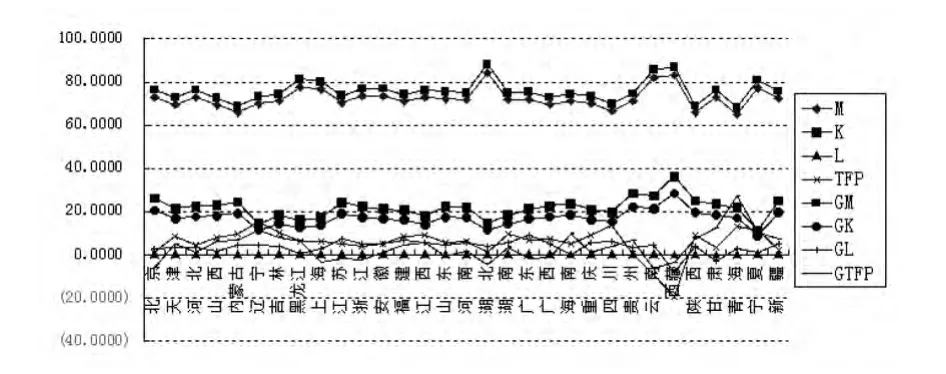
图1 引入环境变量前后中国省份工业经济增长核算结果对比：2003-2012

显然，图中的结果显示，是否引入环境变量对经济增长核算结果具有较大的影响，其中不引入环境变量时无一例外地低估了（高估）原材料（资本）投入的贡献，同时还低估（高估）了大多数省份劳动力投入（全要素生产率变化）的贡献，总体结论与Elsadig（2007）、罗岚（2012）、杨文举（2011）、杨文举和龙睿赟（2012）的研究一致。为从统计检验的角度对这种差异性结论进行验证，我们对是否引入环境变量的经济增长核算结果进行配对T检验，结果见表4。检验结果显示，原材料、资本、劳动力和全要素生产率的贡献率基本上都至少在1%的显著性水平上拒绝了两种思路下测度结果无差异的原假设，例外的是全要素生产率的贡献率只是在10%的显著性水平上拒绝了两种思路下测度结果无差异的原假设，这表明是否考虑非期望产出对测度结果是具有明显影响的，即在两种情况下是具有显著差异的，这与相关研究结论一致，如杨文举（2011）、杨文举和龙睿赟（2012）。

表4 中国省份工业经济增长核算结果配对T检验结果

4 结语

本文在相关研究的基础上，结合完全竞争和规模报酬不变的双重假定，将原材料（用中间品表示）、环境变量（用二氧化硫和化学需氧量表示）与资本和劳动力一起，引入1个描述工业总产出的总量生产函数，在一定程度上扩展了传统的索洛增长核算模型，将资源和环境双重约束下的总产出增长率分解为投入要素积累（包括原材料、资本和劳动力）、全要素生产率增长和环境投入变化等源泉；并以中国大陆31个省份的工业为样本进行了相应的经验分析，扩展了该领域的研究对象。研究结论表明，2003～2012年间，中国工业经济增长的主要源泉在于原材料和资本等要素投入而非生产效率提升；各种投入（含环境投入）对中国工业经济增长的贡献作用具有较大差异，这不仅体现为各自的相对贡献率大小各有不同，而且还体现为所有投入贡献率的省际差异较大；是否引入环境变量对经济增长核算结果具有显著影响，其中不引入环境变量时无一例外地低估了（高估）原材料（资本）投入的贡献，同时低估（高估）了大多数省份劳动力投入（全要素生产率变化）的贡献，总体结论与大多数相关研究结论一致。

显然，本文的这些结论不仅表明在经验分析中进行绿色经济增长核算十分必要，而且还意味着我国工业发展仍未超越要素积累的粗放型经济增长阶段，特别是原材料和物质资本投入在工业总产出增长中占据了相当大的重要推动作用。与此同时，全要素生产率进步为代表的技术水平和技术效率的提升也对我国近年来的工业发展做出了较大贡献，但仍然具有比较大的上升空间。值得一提的是，成功的减排也是有助于经济增长的，其原因在于非期望产出的缩减会变相地增加期望产出的资源投入从而促进经济增长，这从本文的经验研究结论中环境污染变量的产出弹性为负数可以得知。显然，为促进中国工业经济科学发展，我们还有巨大的发展空间，但是这必须依赖于大幅提升全要素生产率水平，进而促进节能减排和绿色增长。因此，深入研究工业绿色全要素生产率的影响因素及其增长路径，是该领域值得深入的重要方向。

[1]Elsadig M A.Biochemical Oxygen Demand Emissions Impact On Malaysia’S Manufacturing Productivity Growth[J].Global Economic Review,2007,(36).

[2]Elsadig M A.Green TFP Intensity Impact on Sustainable East Asian Productivity Growth[J].Economic Analysis&Policy,2012,(1).

[3]Jorgenson D W ，Griliches.Z，The Explanation of Productivity Change[J].Review of Economic Studies,1967,(34).

[4]Repetto R,Rotham D,Faeth P,et al.Productivity Measures Miss The Value of Environmental Protection[J].Choices,1997,(4).

[5]陈诗一.能源消耗、二氧化碳排放与中国工业的可持续发展[J].经济研究,2009,(4).

[6]罗岚.我国资源和环境对经济增长贡献测度[J].四川师范大学学报（社会科学版）,2012,(3).

[7]王奇,王会,陈海丹.中国农业绿色全要素生产率变化研究:1992-2010年[J].经济评论,2012,(5).

[8]薛建良,李秉龙.基于环境修正的中国农业全要素生产率度量[J].中国人口·资源与环境,2011,(5).

[9]杨文举.基于DEA的绿色经济增长核算:以中国地区工业为例[J].数量经济技术经济研究,2011,(1).

[10]杨文举,龙睿赟.中国地区工业绿色全要素生产率增长：基于方向性距离函数的经验分析[J].上海经济研究,2012,(7).