一种适用于继电保护在线整定的极小断点集求取算法

任康杰，刘 阳，李 勇，金明亮，李银红

一种适用于继电保护在线整定的极小断点集求取算法

任康杰1，刘 阳2，李 勇2，金明亮2，李银红1

(1.强电磁工程与新技术国家重点实验室(华中科技大学)，湖北 武汉 430074；2.国家电网公司华中分部，湖北 武汉 430077)

复杂环网中继电保护在线整定的顺利进行依赖于极小断点集的快速求取，但现有极小断点集求取算法在算法复杂度、断点集维数及计算效率等方面还存在不足。对此，提出了一种适用于继电保护在线整定的极小断点集求取算法。该方法基于图论中基本割集矩阵与基本回路矩阵的固有关系，将复杂环网的断点集求取问题转换成了基于基本割集矩阵的基本回路断点集求取问题。通过动态调整基本割集矩阵，逐步计算得到网络极小断点集。算例分析表明，所提算法能够在有效的时间内求得网络极小断点集，大大降低了问题的复杂性。

继电保护在线整定；环网方向保护；极小断点集；基本割集矩阵；基本回路矩阵

0 引言

继电保护是保证电力系统安全运行的重要保障，保护的合理配置是确保其可靠发挥作用的关键[1-7]。现有高压环形电网一般配置了基于双端信息的纵联保护作为主保护；同时，为了应对通信通道故障导致的主保护拒动工况[8]，还配置了基于单端信息的电流保护、距离保护作为后备保护；主保护和后备保护共同作用，确保保护装置动作的正确性[9]。然而，由于后备保护仅仅基于单端信息，存在邻近元件故障时本保护误动的可能性。而且，现有电网普遍采用了“离线整定、在线不变”的保护定值管理模式。因此，在电网整定计算工作中，着重对各种运行方式下后备保护与相邻保护的配合进行了协调，确保在线运行时后备保护动作的正确性。

随着电力系统的迅速发展，电网逐渐向节点数目巨大、回路错综复杂、运行方式多变的方向发展，传统的继电保护离线整定模式难以跟踪系统运行方式的变化，保护定值性能也因考虑最严苛的运行方式而难以达到最佳[10-14]。在此背景下，研究适应电网运行方式变化的继电保护在线整定模式具有重要的意义[15-17]。复杂环网的整定计算首先需要确定最小断点集，即环网中整定计算的起始点，但是，最小断点集的求取往往需要耗费大量时间[18-22]。考虑到在线整定计算对计算效率有较高的要求，因此，在线整定计算一般要求在保证计算效率的前提下尽可能确定出断点数目接近最小的断点集，本文称该断点集为极小断点集(Minimal Break Point Set, MBPS)。

为了进一步提高在线整定计算中的断点集求取效率，部分文献针对在线整定中电网拓扑结构往往仅发生局部变化的特点，开展了基于离线确定最小断点集、根据拓扑变化更新断点的断点集求取方法研究。文献[23]提出了一种在网络拓扑结构变化时利用虚拟断点集快速更新断点集的新方法，通过处理少量的元素即可实现全网断点集的更新。文献[24]提出了一种适应任意拓扑结构变更的断点集更新方法，该方法根据线路投退和母联开关开合后简单回路变化特性推导出断点演化规律，并据此进行断点的更新。这类方法根据网络结构的变化更新保护关联矩阵，只需处理部分元素即可实现全网断点集的更新。此类方法在电网运行方式出现较大变化时，算法复杂度增加，且求出的断点集可能从整个电网来看并不是较优的极小断点集。

部分文献研究了计算效率较高的大规模电网全网断点集求取方法，适用于在线整定计算。文献[25]提出保护依赖度的概念，通过所有保护依赖度大小的比较确定断点集。此方法计算时间规模是保护总数的多项式函数。文献[26]提出了基于矩阵运算的断点集求取算法，该方法只需对网络关联矩阵进行LU分解，用得到的下三角矩阵进行断点的选取。此类算法能够较快实现大规模网络极小断点集的求解，但断点集维数和计算效率还有进一步优化的空间。

基于此，本文提出了一种适用于继电保护在线整定的极小断点集求取算法。首先，通过基本割集矩阵与基本回路矩阵之间的固有关系，提出了一种基于基本割集矩阵的基本回路断点确定方案。然后，证明了所确定的基本回路断点能够断开所有简单回路，由此将复杂环网的断点集求取问题转换成了基于基本割集矩阵的基本回路断点集求取问题。进一步地，为了求取极小断点集，通过动态调整基本割集矩阵逐步计算得到网络极小断点集。最后，算例分析结果表明本文所提出的极小断点集求取方法在保证时效性的同时，优化了断点集维数，满足继电保护在线整定的要求。

1 电力系统图的矩阵描述和断点

1) 基本割集矩阵

基本割集矩阵是描述有向图中基本割集与支路相互关联情况的矩阵，中元素的定义如式(1)所示。

如果按照先连枝后树枝的顺序排列，则矩阵可写成分块矩阵的形式，如式(2)所示。

式中：阵与连枝对应，称为连枝矩阵；与树枝对应，且为单位矩阵。

2) 基本回路矩阵

基本回路矩阵是描述有向图中基本回路与支路相互关联情况的矩阵，中元素的定义如式(3)所示。

如果按照先连枝后树枝的顺序排列，则可写成分块矩阵的形式，如式(4)所示。

式中：阵与连枝对应，且为单位矩阵；阵与树枝对应，称为树枝矩阵。

3)与之间的内在联系

对于同一有向图的阵和阵，两者存在内在联系，如式(5)所示[27]。

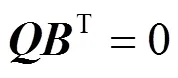
4) 示例

以图1所示的某7节点网络为例，规定节点编号小者为支路起点，节点编号大者为支路终点。

图1 7节点网络方向保护配置图

其基本割集矩阵如图2所示，其中表示基本割集，表示支路。

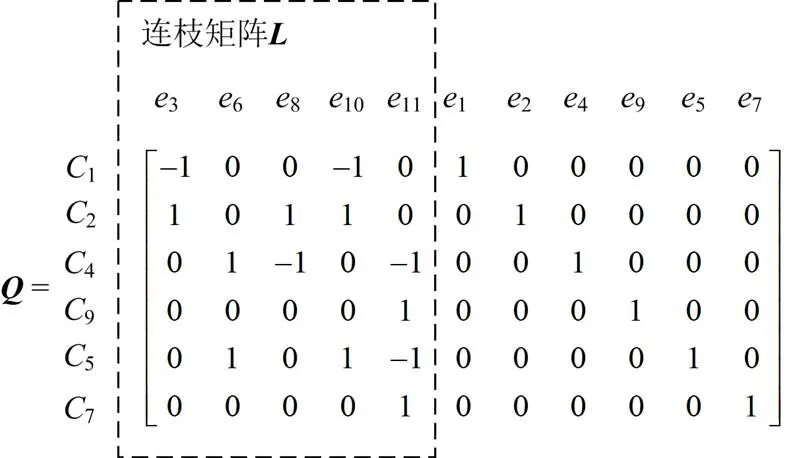
图2 基本割集矩阵示意图

其基本回路矩阵如图3所示，其中表示基本回路，表示支路。

图3 基本回路矩阵示意图

此外，将中所有元素取负，就可以得到另一方向的基本回路矩阵-，如图4所示。

5) 断点

一般来说，电力系统每一支路两侧都配置了方向保护，相邻支路同一方向上的保护之间存在配合关系。如图1所示，支路1起点1侧保护，即与支路3和10起点2侧保护之间存在配合关系。当这种配合关系形成回路时，则整定计算无法开展。例如，支路1起点1侧保护、支路3起点2侧保护、支路2终点4侧保护，即构成了配合关系回路。这时，就必须选择某个保护作为断点，断开该回路，保证其他保护整定的顺利进行。考虑到被选作断点的保护可能需要牺牲保护选择性或者灵敏性，因此，一般选取能够断开所有配合关系回路的最小断点集。而且，如果母线上下一级线路带有重要电源或者重要负荷，一般不选作断点。

图4 另一方向基本回路矩阵示意图

对于任一电力系统，方向保护间的任一配合关系回路，总是可以表示为该系统有向图的某一简单回路。仍以图1为例，支路1起点1侧保护、支路3起点2侧保护、支路2终点4侧保护构成的配合关系回路可以表示为有向图的某一简单回路，描述如图5所示。

图5 某一简单回路示意图

该行中的非0元素，即代表了构成配合关系回路的一组保护，1代表对应支路起点侧保护，-1代表对应支路终点侧的保护。因此，求取最小断点集，即为找到一组能够断开该系统有向图所有简单回路的最小保护。

而最小断点集的求解是一个具有指数复杂度的NP完全问题，对于大规模复杂环网，要求得最小断点集十分困难，往往需要耗费大量的时间。考虑到在线整定计算首先需要保证计算效率，因此，在线整定计算中通常要求确定出接近最小的断点集，即极小断点集。然而，现有极小断点集求取算法在算法复杂度、断点集维数、计算效率等方面还存在不足。针对这一现状，本文提出了一种适用于继电保护在线整定的极小断点集求取算法，将复杂环网的断点集求取问题转换成了基于基本割集矩阵的基本回路断点集求取问题，基本割集矩阵规模小，保证了断点集求取的快速性。

2 基于基本割集矩阵的基本回路断点确定方案

由于基本回路矩阵和基本割集矩阵之间存在等式关系(5)，则通过基本割集矩阵，即可以确定出一组能够断开所有基本回路的断点。定义基本割集矩阵中的每个基本割集向量(即阵行向量)称作的一个子集。具体方案如下：

1) 选取基本割集矩阵的任一子集，将其中属于连枝矩阵中的每一个非0元素对应支路保护选为断点，其中非0元素1表示支路起点侧方向保护，-1表示支路终点侧方向保护。则这些断点可以在一个方向上断开由所有非0元素对应连枝决定的所有基本回路，即(-)矩阵中的基本回路。

2) 将同一子集中属于树枝矩阵中的非0元素1对应支路保护选为断点，即支路起点侧保护。则该断点可以从另一个方向断开由同一行所有非0元素对应连枝决定的所有基本回路，即-()矩阵中的基本回路。

3) 将已选子集依次置于一个新的矩阵中，下称判断矩阵，然后在中删除已选子集，以及已选连枝断点对应列。若判断矩阵的连枝矩阵每一列都至少有一个非0元素，则结束，否则，返回1)。

基于上述步骤，即可确定出一组能够断开所有基本回路的断点。不失一般性，以图1为例，说明上述步骤确定的基本回路断点的正确性。

式(5)表示和的任意行之间点乘为0。不失一般性，取和的第一行进行分析，如图6所示。

图6 B第一行(上)与Q第一行(下)点乘示意图

当和均按照先连枝后树枝的顺序排列时，由和的结构可知，和任意行之间乘积实际上最多只涉及两个位置的乘积。如图6中虚线所示，和第一行之间的乘积只涉及两个位置元素的乘积，其中一个位置为连枝，另一个位置为树枝。并且当一个位置的两个元素同号(异号)时，另一个位置的两个元素一定是异号(同号)的。

中非0元素代表环路一个方向上的保护，-中非0元素代表环路另一个方向上的保护，和-即构成了两个方向的基本回路矩阵，如图7所示。只有两个方向上的基本回路中均有保护被选作断点，才能断开两个方向的基本回路。

图7 两个方向的基本回路矩阵示意图

若将中任一子集某一连枝保护选为断点，如图8所示，则该连枝保护可以在一个方向上断开由该连枝决定的基本回路，在图8中表现为11可以在一个方向上(图4中-)断开连枝3决定的基本回路。如果再将中同一子集树枝矩阵中非零元素对应保护选为断点，则树枝矩阵中的断点一定可以断开另一个方向上的基本回路，在图8中表现为16可以在另一个方向上(图4中)断开连枝3决定的基本回路。

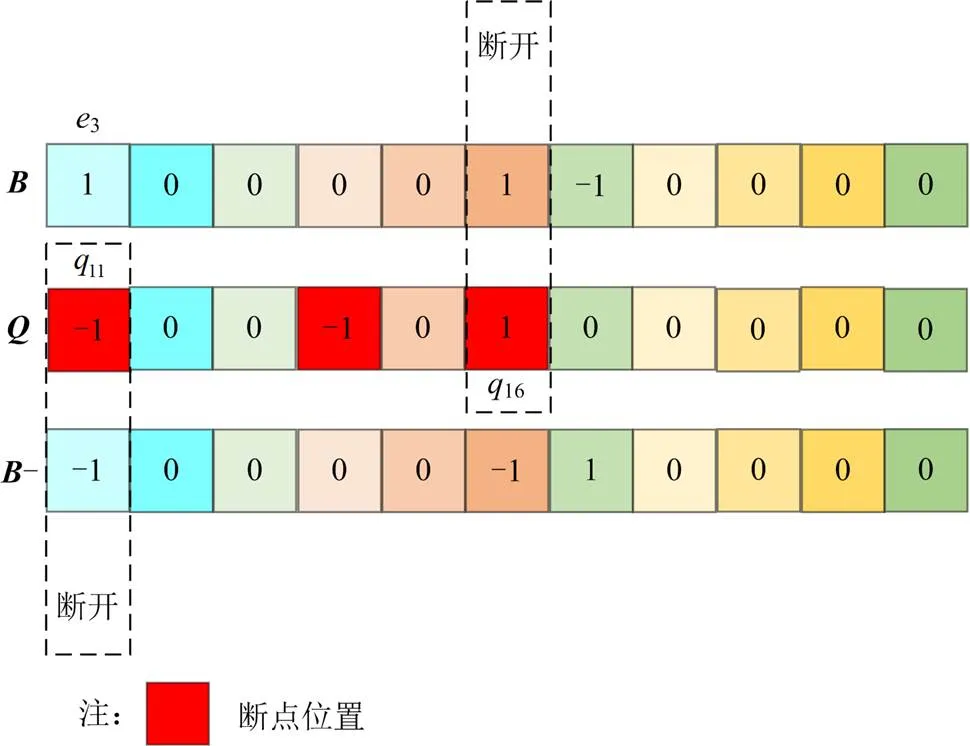
图8 断点选取示意图

由上述断点选取过程可知，中连枝矩阵内部非零元素对应保护即为连枝断点，可从一个方向上断开该连枝决定的基本回路，对应子集中的树枝上的保护即为树枝断点，可从另一个方向上断开该连枝决定的基本回路。那么若将中任一子集所有连枝保护选为断点，则这些连枝保护可以在一个方向上断开由这些连枝决定的基本回路，再将中同一子集树枝矩阵中非零元素对应保护选为断点，则树枝矩阵中的断点一定可以断开另一个方向上的基本回路。以其中一个子集为例对此进行说明，如图9所示，将连枝6的起点侧、8和11的终点侧、树枝4的起点侧保护选为断点，则连枝6、8、11上的断点可以分别断开一个方向上6、8、11决定的基本回路，树枝4上的断点可以在与连枝断点相反方向上断开6、8、11决定的3个基本回路。

图9 Q中某一子集示意图

综上所述可知，中任一子集均可选出一个树枝断点和多个连枝断点，且树枝断点断开与连枝断点相反方向的基本回路。那么通过选择的子集，构成判断矩阵，直到的连枝矩阵每一列都至少有一个非0元素，中非0元素即为所求基本回路断点，此时所有连枝断点在一个方向上断开所有基本回路，所有树枝断点断开与连枝断点相反方向的基本回路。其中非0元素1表示支路起点侧方向保护，-1表示支路终点侧方向保护。

3 基本回路断点的所有简单回路开断特性

第2节提出了基于基本割集矩阵的基本回路的断点确定方案，而且，该方案确定的基本回路断点具有能够断开所有简单回路的特性。下面对这一特性进行简单说明。

根据图论的基本知识，得到以下结论。

结论1：任何一个简单回路必定是若干个基本回路的组合[28]。

结论2：若干个基本回路组合成一个简单回路时，只可能消除树枝，不可能消除连枝。

基本回路组合可分为两种情况：两个基本回路组合成一个简单回路和多个基本回路组合成一个简单回路。下面对两种情况分别进行分析。

1) 两个基本回路的组合

根据基本回路与共有树枝的正方向不同可以分为图10所示的3种情况，分别是两回路正方向均与共有树枝方向相同、两回路正方向均与共有树枝方向相反和仅有一个回路正方向与共有树枝方向相同。下面对这3种情况分别进行分析。

首先对断点的位置进行说明，由上述可知，和任意行之间乘积实际上最多只涉及两个位置的乘积，故仅考虑这两个位置的元素对3种情况进行分析，如图11所示。由于阵中树枝矩阵非0元素一定为1，即图11中阵的树枝矩阵一列全为1，所以树枝断点一定位于树枝起点；由于连枝方向与基本回路正方向相同，所以阵中连枝矩阵非0元素一定为1，即图11中阵的连枝矩阵一列全为1。

图10 基本回路组合示意图

当两回路正方向与共有树枝方向相同时，此时两个回路阵的树枝部分应全为1，如图11所示。在满足阵和阵两行的点乘为0的条件下，阵的连枝部分必须为-1，即连枝断点均位于连枝终点，如图10(a)所示。从图中可见，两个基本回路组合成一个简单回路后，保护配合关系如图中黑色虚线箭头所示。可以看出，断点可以在两个方向上断开组合后的简单回路。

当两回路正方向与共有树枝方向相反时，此时两个回路阵的树枝部分应全为-1，如图11所示。在满足阵和阵两行的点乘为0的条件下，阵的连枝部分必须为1，即连枝断点均位于连枝起点，如图10(b)所示。从图中可见，两个基本回路组合成一个简单回路后，保护配合关系如图中黑色虚线箭头所示。可以看出，断点可以在两个方向上断开组合后的简单回路。

当仅有一个回路正方向与共有树枝方向相同时，此时方向相同的基本回路阵树枝部分为1，方向相反的基本回路阵树枝部分为-1，如图11所示。在满足阵和阵两行的点乘为0的条件下，阵的连枝部分一个为1，一个为-1，即连枝断点一个位于连枝起点，一个位于连枝终点，如图10(c)所示。从图中可见，两个基本回路组合成一个简单回路后，保护配合关系如图中黑色虚线箭头所示。可以看出，断点可以在两个方向上断开组合后的简单回路。

图11 连枝断点位置推导示意图

2) 多个基本回路的组合

若一个简单回路1由两个以上的基本回路组合而成，可看作两个基本回路组合成一个简单回路2后与其他基本回路组合，在此过程中2中的两个连枝始终不会消除，这代表简单回路1也始终包含这两个连枝，那么在这两个连枝上所取的断点始终能断开两个方向上的简单回路。

从上述分析可知，所提基本回路断点确定方案能够断开全网简单回路。通过选取中不同子集，直到判断矩阵的连枝矩阵每一列都至少有一个非0元素，那么中的非0元素即为所求断点，即为能够断开网络中所有简单回路的断点。

4 MBPS求取算法流程

前两节将复杂环网的断点求取问题转换成基于基本割集矩阵的基本回路断点求取问题。通过选择基本割集矩阵的子集，构成判断矩阵，使得矩阵的连枝矩阵每一列至少有一个非0元素，那么矩阵中的非0元素即为所确定的断点。但是，如果子集选择的顺序不同，会导致所确定的断点数量不同。由所提方案可知，断点数量等于连枝数量与所选择的子集数之和，故断点集的求解问题就转换成了矩阵子集的选取问题。基于此，为了提高MBPS求取效率，本文提出通过比较基本割集矩阵中非0元素的数量选择子集，并通过动态调整基本割集矩阵逐步计算求得网络极小断点集。

定义的子集中非0元素的数量称作子集的特征值，子集中所有元素的数量称作子集的长度。把所有子集分成3个集合：决策集past、当前搜索集now和辅助更新集update。

需要说明的是，决策集存放所有决策结果，搜索集存放所有子集，辅助更新集存放本次决策结果。在每一步决策之后，搜索集now均会根据每次决策结果update更新所有子集长度和特征值，即删除update中非0元素对应列，去除已选断点连枝对决策的影响，优化下一次决策的结果。

而且，考虑到在实际的电力网络中，存在一些特殊网络拓扑，如长短线配合、平行双回线等，这些特殊的网络结构往往会被优先选择作为断点。而且，还存在一些特殊网络结构，例如母线上下一级线路带有重要电源或者重要负荷，这些特殊网络结构一般不被选作断点。对此，本文所提算法具有较高的灵活性，可通过将对应支路优先级提高或者降低的方式，优先或者延后选择该支路所在的行，即优先或者延后选择该支路上的保护作为断点。下面以网络含平行双回路为例对算法步骤进行详细说明。

算法的流程图如图12所示，详细的步骤如下：

1) 进行网络初始化，确定基本割集矩阵；

2) 计算所有子集的特征值并将所有子集加入now中；

4) 计算now中所有子集特征值，根据特征值大小对now中子集从大到小排序；

5) 搜索now，找到特征值最大的子集1，即now中的第一个子集；

7)now删除update中非0元素对应列，则now中子集长度和特征值会随着若干列的删除发生改变；

8) 若满足past中连枝矩阵每一列都至少有一个非0元素，结束，转步骤9)；否则，转步骤4)；

9)past中子集即为决策结果，从第一个子集开始，在保证每一连枝只取一断点的前提下(即连枝矩阵每一列只有一个非0元素取为断点)，将其中非0元素位置取为断点，1表示将支路起点保护取为断点，-1表示将支路终点保护取为断点，值得一提的是，若矩阵中非0元素所在列所表示的支路为平行双回路，则两条支路均按照上述原则在相同位置设为断点。

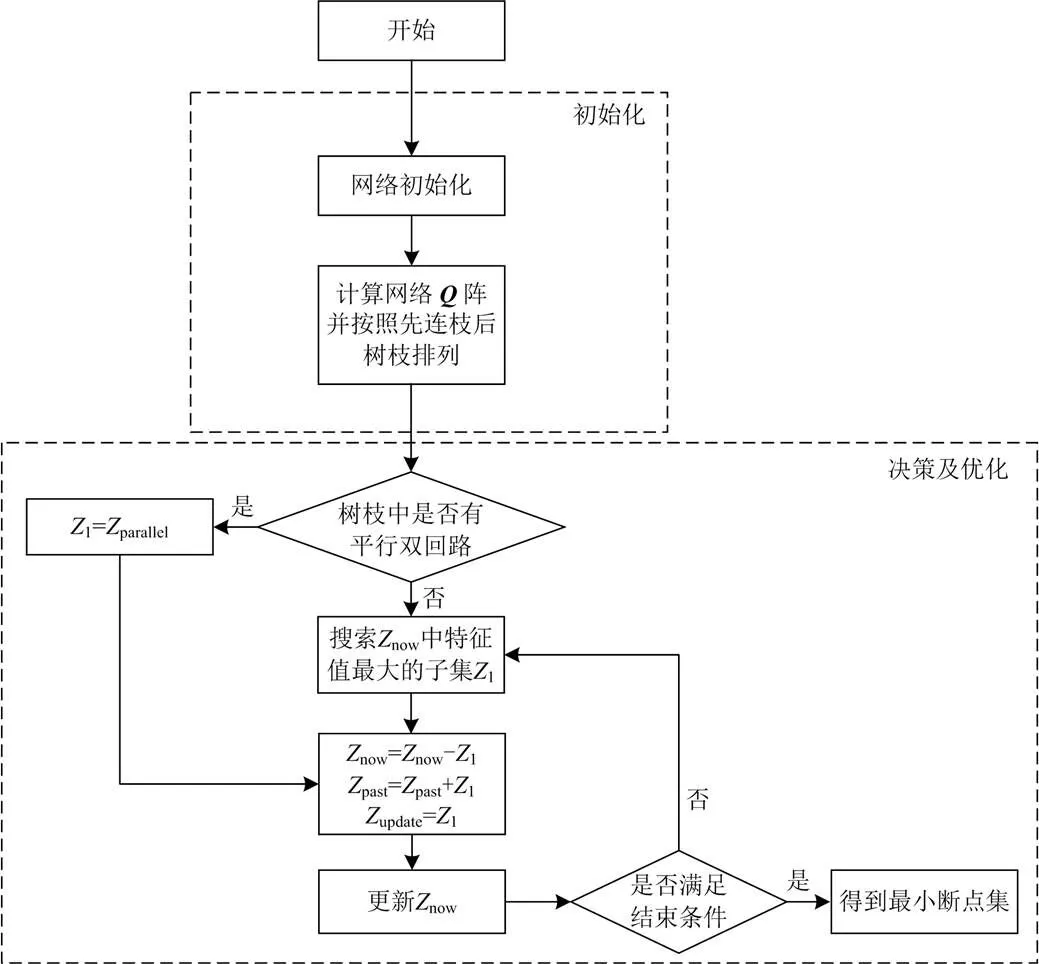
图12 所提算法求取MBPS流程图

5 算例分析

以4个IEEE标准节点网络[29]和某省级500 kV电网[30]为算例系统来验证所提算法的有效性，仿真实验基于Matlab进行编程测试，PC配置为Inter(R) Core(TM) i5-7300HQ CPU 2.5 GHz/RAM 8 GB。

5.1 算例结果

下面将本文所提算法应用于4个IEEE标准节点网络和某省级500 kV电网中，仿真结果如表1所示。其中IEEE14节点网络、IEEE30节点网络最小断点集展示如下。IEEE14节点网络所求断点为{5→2，5→4，11→10，13→14，4→3，9→7，13→12，1→2，2→3，4→7，6→12}，断点示意图如图13所示；IEEE 30节点网络所求断点为{9→10，20→10，17→10，23→24，8→28，6→28，3→4，6→4，6→7，22→21，15→14，30→29，6→10，2→4，2→5，10→21，12→14，27→29}，断点示意图如图14所示。可以看出，所选断点均能够断开网络中所有简单回路，并且随着网络规模的扩大，MBPS的计算时间始终维持在一个极短的时间内，具有较高的时效性。

为验证所提算法的实用性，将本文所提算法应用于某省级500 kV电网，电网示意图如图15所示，所求断点为{13→4，13→9，13→11，13→12，13→14，8→9，22→24，30→25，6→8，13→36(2)，2→17(2)，4→26(2)，6→9(2)，6→20(2)，6→23(2)，7→25(2)，7→22(2)，9→10(2)，12→14(2)，18→34(2)，21→23(2)，21→24(2)，22→34(2)，22→30(2)，29→30(2)，33→34(2)，6→7}，其中平行双回线被选作断点时，两条线路均在相同位置设置断点，如上述文中标(2)处。从表1中可以看出，所求断点数目为44，计算时间仅需1.255 ms，时效性较高。

表1 典型网络中所求断点数量及所用时间

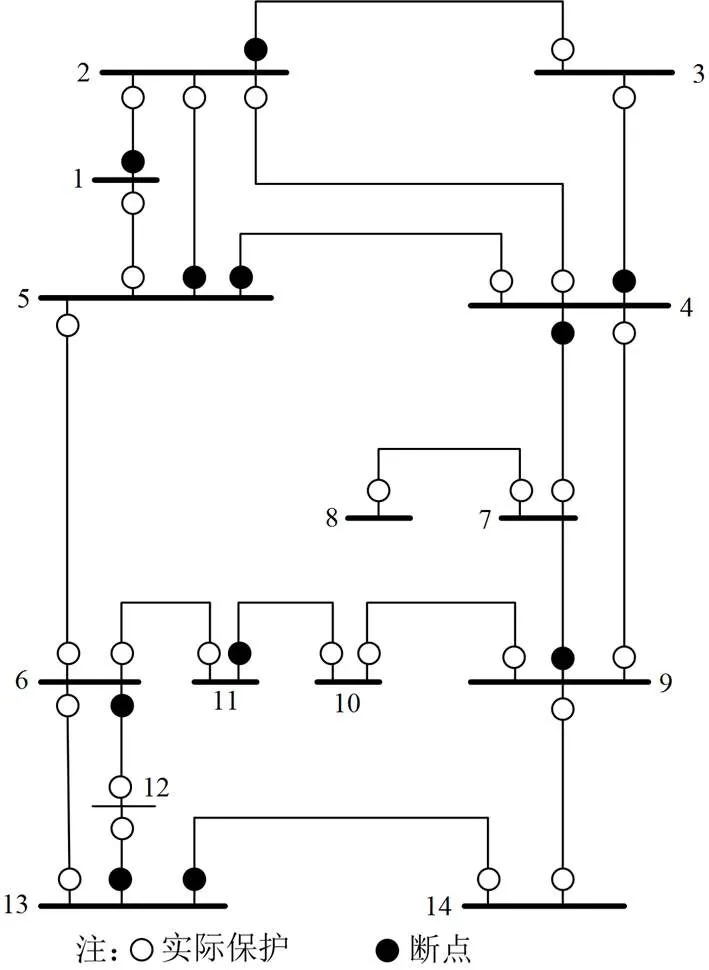
图13 IEEE14节点网络断点示意图

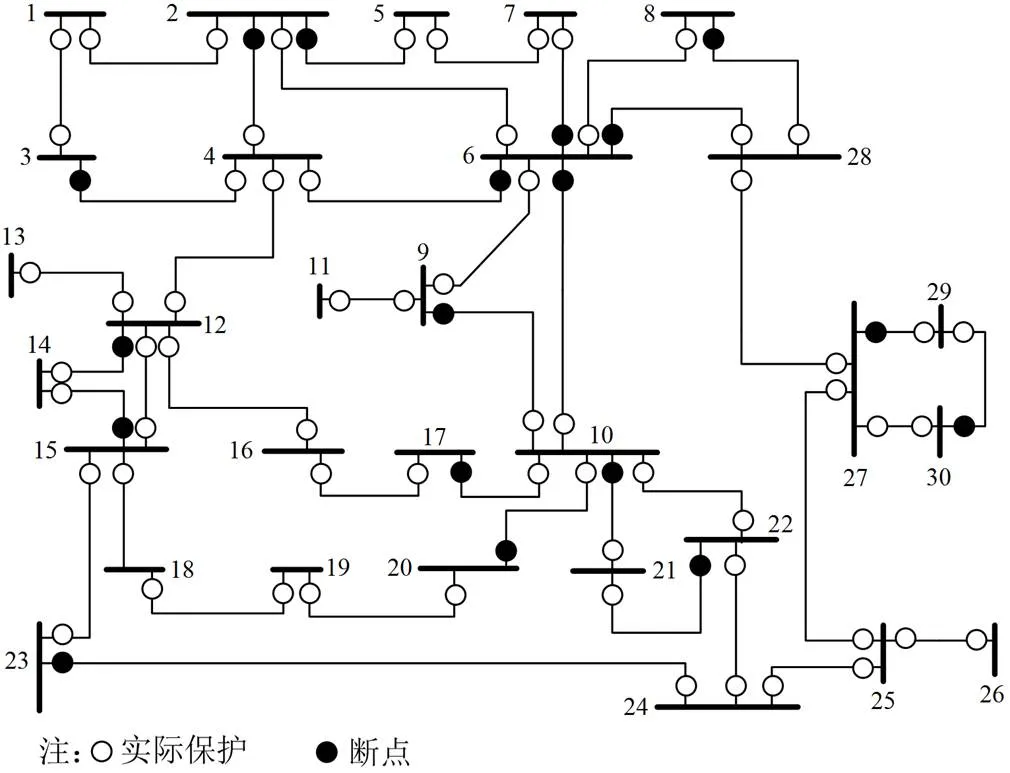
图14 IEEE30节点网络断点示意图

图15 某省级500 kV电网示意图

5.2 方法比较

本文所提算法目的是希望在较短的时间内求出极小断点集，以适用于继电保护在线整定。故在断点数量与计算时间两个方面，与现有文献提出的极小断点集求取算法进行对比。文献[25]提出通过所有保护依赖度大小的比较确定断点集；文献[26]提出根据网络关联矩阵LU分解后得到的下三角矩阵进行断点的选取。

选取的3个不同的IEEE标准节点网络，对比结果如表2和表3所示。值得说明的是，表中平均计算时间为程序重复运行10次的平均计算时间，且文献[25]在保护依赖度相同时会任选其一作为断点，故断点的结果存在随机性，本文所用结果为程序重复运行10次的最小值。

表2 不同MBPS求取算法下断点数量对比

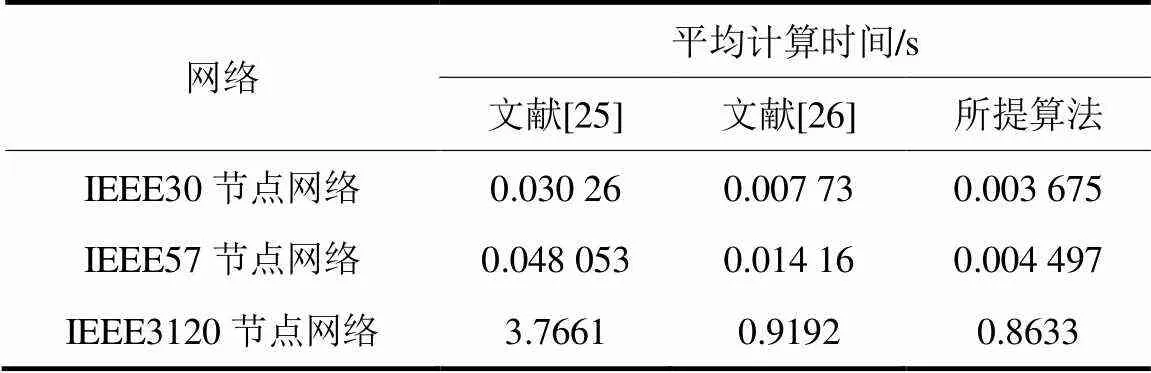
表3 不同MBPS求取算法下计算时间对比

本文所提算法与文献[26]相比，在断点数量上，在IEEE30、57、3120节点网络下依次减少了8、6、586个断点；在平均计算时间上，在IEEE30、57、3120节点网络下依次节省了87.8%、90.6%、77.1%；造成上述差异的原因为文献[26]所形成的保护依赖度集规模较大，且保护依赖度集的更新较复杂。

本文所提算法与文献[26]相比，在断点数量上，在IEEE30、57、3120节点网络下依次减少了1、1、153个断点；在平均计算时间上，本文所提算法略低于文献[26]；造成上述差异的原因为：文献[26]在非对称矩阵的LU分解上花费了较多时间，且在后续决策过程未及时更新下三角矩阵。

综上所述，本文所提算法在断点数量和求解效率上均取得了较好的效果。与已有研究相比，在保证时效性的同时，进一步优化了断点数量，满足继电保护在线整定的要求。

6 结语

本文提出了一种适用于继电保护在线整定的极小断点集求取方法。该方法通过基本割集矩阵和基本回路矩阵之间的内在联系，将复杂环网断点集求取问题转换成了基于基本割集矩阵的基本回路断点集求取问题，并通过动态调整基本割集矩阵逐步计算得到网络极小断点集。该算法有以下优点：1) 算法求解效率高，适用于在线整定计算；2) 算法灵活性高，可以凭借专家经验设置支路优先级，优先或者延后选择特殊结构作为断点；3) 算法适用性高，通过调节网络树、连枝的选择可得到多组最小断点集。

[1] KHOND S V, DHOMANE G A. Optimum coordination of directional overcurrent relays for combined overhead/ cable distribution system with linear programming technique[J]. Protection and Control of Modern Power Systems, 2019, 4(2): 114-120.

[2] BO Zhiqian, LIN Xiangning, WANG Qingping, et al. Developments of power system protection and control[J]. Protection and Control of Modern Power Systems, 2016, 1(1): 1-8.

[3] 谭振龙, 钱相宜, 蔡文畅. 配置高抗站的海上风电长距离海缆送出继电保护分析[J]. 中国电力, 2021, 54(8): 175-181.

TAN Zhenlong, QIAN Xiangyi, CAI Wenchang. Analysis of relay protection for offshore wind power long-distance submarine cable transmission with high resistance station[J]. Electric Power, 2021, 54(8): 175-181.

[4] 李红志, 王彪, 陈卉, 等. 基于混合专业词典的继电保护定值在线智能比对方法[J]. 广东电力, 2020, 33(4): 58-66.

LI Hongzhi, WANG Biao, CHEN Hui, et al. Intelligent online check of relay protection setting based on hybrid professional dictionary[J]. Guangdong Electric Power, 2020, 33(4): 58-66.

[5] 王杨正, 杨建明, 鲁江, 等. 配置HSS的并联多端高压直流输电线路保护选择性研究[J]. 电力工程技术, 2020, 39(1): 95-102.

WANG Yangzheng, YANG Jianming, LU Jiang, et al. Line protection selectivity of the parallel multi-terminal HVDC with HSS[J]. Electric Power Engineering Technology, 2020, 39(1): 95-102.

[6] 桂海涛, 陈宏山, 李任明. 基于继电保护数据分析的配电网供电可靠性提升策略研究[J]. 供用电, 2020, 37(6): 53-59.

GUI Haitao, CHEN Hongshan, LI Renming. Research on strategy of distribution network power supply reliability improvement based on relay protection data analysis[J]. Distribution & Utilization, 2020, 37(6): 53-59.

[7] 常俊晓, 应宇鹏, 廖小兵, 等. 基于图像处理的继电保护装置定值自动核对方法[J]. 电测与仪表, 2021, 58(11): 67-73.

CHANG Junxiao, YING Yupeng, LIAO Xiaobing, et al. The automatic checking method of setting value for relay protection device based on image processing[J]. Electrical Measurement & Instrumentation, 2021, 58(11): 67-73.

[8] 王英英, 金明亮, 王玉龙, 等. 应对线路差动主保护丢失的后备保护应急方案[J]. 电力系统保护与控制, 2021, 49(7): 174-181.

WANG Yingying, JIN Mingliang, WANG Yulong, et al. Emergency plan for backup protection against loss of line differential main protection[J]. Power System Protection and Control, 2021, 49(7): 174-181.

[9] 220 kV～750 kV电网继电保护装置运行整定规程: DL/T 559—2007[S].

[10] 段献忠, 杨增力, 程逍. 继电保护在线整定和离线整定的定值性能比较[J]. 电力系统自动化, 2005, 29(19): 58-61.

DUAN Xianzhong, YANG Zengli, CHENG Xiao. Performance analysis of relay settings determined according to off-line calculation and on-line calculation[J]. Power System Protection and Control, 2005, 29(19): 58-61.

[11] 李怀强, 高露, 粟小华, 等. 基于非最严苛电网运行方式的超高压线路距离保护整定方法[J]. 电力系统保护与控制, 2020, 48(21): 166-172.

LI Huaiqiang, GAO Lu, SU Xiaohua, et al. A distance protection relay coordination method for EHV transmission lines based on non most severe grid operation mode[J]. Power System Protection and Control, 2020, 48(21): 166-172.

[12] 孙正伟, 刘家庆, 鲍斌, 等. 超高压电网反时限零序过流保护简化整定方法[J]. 电力系统保护与控制, 2020, 48(17): 18-26.

SUN Zhengwei, LIU Jiaqing, BAO Bin, et al. A novel simplified relay coordination method for inverse-time zero-sequence overcurrent relays applied in an extra-high voltage power grid[J]. Power System Protection and Control, 2020, 48(17): 18-26.

[13] 孙楠, 严佳梅, 赵俊, 等. 特高压换流站站用电系统保护配置及定值配合研究[J]. 广东电力, 2021, 34(8): 86-93.

SUN Nan, YAN Jiamei, ZHAO Jun, et al. Research on protection configuration and setting coordination of UHV converter station power system[J]. Guangdong Electric Power, 2021, 34(8): 86-93.

[14] 焦飞, 闫冬, 李仲青, 等. 基于改进离散花授粉算法的继电保护定值优化方法的研究[J]. 智慧电力, 2021, 49(5): 48-55.

JIAO Fei, YAN Dong, LI Zhongqing, et al. Relay protection setting optimization based on improved discrete flower pollination algorithm[J]. Smart Power, 2021, 49(5): 48-55.

[15] 吕颖, 吴文传, 张伯明, 等. 电网保护定值在线整定系统的开发与实践[J]. 电网技术, 2008, 32(8): 15-20.

LÜ Ying, WU Wenchuan, ZHANG Boming, et al. Development and application of an on-line relay setting coordination system[J]. Power System Technology, 2008, 32(8): 15-20.

[16] 陈新, 吕飞鹏, 蒋科, 等. 基于多代理技术的智能电网继电保护在线整定系统[J]. 电力系统保护与控制, 2010, 38(18): 167-173.

CHEN Xin, LÜ Feipeng, JIANG Ke, et al. Protective relaying on-line coordination and calculation system of smart grid based on MAS[J]. Power System Protection and Control, 2010, 38(18): 167-173.

[17] 王增平, 刘国平, 仇向东, 等. 继电保护定值在线整定功能的实现[J]. 电力系统保护与控制, 2012, 40(1): 127-130.

WANG Zengping, LIU Guoping, QIU Xiangdong, et al. Realization of online relay protection setting value adjustment[J]. Power System Protection and Control, 2012, 40(1): 127-130.

[18] SIDHU T S, BALTAZAR D S, PALOMINO R M, et al. A new approach for calculating zone-2 setting of distance relays and its use in an adaptive protection system[J]. IEEE Transactions on Power Delivery, 2004, 19(1): 70-77.

[19] 杨文辉, 范生海, 周晓霞. 基于环网方向保护协调配合的最小断点集选取方法[J]. 电力系统保护与控制, 2015, 43(14): 30-34.

YANG Wenhui, FAN Shenghai, ZHOU Xiaoxia. Selection of minimum break point set based on coordination of directional protections in loop grid[J]. Power System Protection and Control, 2015, 43(14): 30-34.

[20] CHEN M, SHI D, DUAN X. A novel minimum break relay dependency set approach for coordination of directional relays in multi-loop networks[J]. IET Generation, Transmission & Distribution, 2017, 11(5): 1279-1285.

[21] GHOTBIMALEKI M, CHABANLOO R M, EBADI M A, et al. Determination of optimal breakpoint set of overcurrent relays using modified depth-first search and mixed-integer linear programming[J]. IET Generation, Transmission & Distribution, 2020, 14(23): 5607-5616.

[22] DOLATABADI M, DAMCHI Y. Graph theory based heuristic approach for minimum break point set determination in large scale power systems[J]. IEEE Transactions on Power Delivery, 2019, 34(3): 963-970.

[23] 马静, 叶东华, 王彤, 等. 适应网络变结构的最小断点集更新算法[J]. 电力系统自动化, 2011, 35(17): 92-98.

MA Jing, YE Donghua, WANG Tong, et al. A method for updating minimum break point set adaptive to variable network configuration[J]. Automation of Electric Power Systems, 2011, 35(17): 92-98.

[24] 晋龙兴, 李银红. 适用于任意拓扑结构变更的最小断点集更新方法[J]. 电力系统自动化, 2013, 37(14): 95-100.

JIN Longxing, LI Yinhong. A method for updating minimum break point set adaptive to arbitrary topology change[J]. Automation of Electric Power Systems, 2013, 37(14): 95-100.

[25] 乐全明, 郁惟镛, 肖燕, 等. 一种计算环网方向保护配合最小断点集的实用算法[J]. 电力系统自动化, 2004, 28(7): 71-74.

LE Quanming, YU Weiyong, XIAO Yan, et al. A practical algorithm to determination minimum break point set for option coordination of directional protective relaying in multiloop networks[J]. Automation of Electric Power Systems, 2004, 28(7): 71-74.

[26] LIU L, FU L. Minimum breakpoint set determination for directional overcurrent relay coordination in large-scale power networks via matrix computations[J]. IEEE Transactions on Power Delivery, 2017, 32(4): 1784-1789.

[27] 汪建, 王欢. 电路原理[M]. 北京: 清华大学出版社, 2016.

[28] 李银红, 段献忠. 继电保护整定计算中形成简单回路的方法[J]. 中国电机工程学报, 2003, 23(2): 20-25.

LI Yinhong, DUAN Xianzhong. Study on the simple loop formation method in relay coordination[J]. Proceedings of the CSEE, 2003, 23(2): 20-25.

[29] MATPOWER: A MATLAB power system simulation package[EB/OL].http://www.pserc.cornell.edu/matpower.

[30] 晋龙兴, 李银红, 石东源, 等. 计及空间分布特性的最小断点集优化求取方法[J]. 电力系统自动化, 2013, 37(7): 60-65.

JIN Longxing, LI Yinhong, SHI Dongyuan, et al. Computing of minimum break point set using optimization algorithm considering its space distribution characteristics[J]. Automation of Electric Power Systems, 2013, 37(7): 60-65.

An algorithm to calculate the minimal break point set for relay protection online setting

REN Kangjie1, LIU Yang2, LI Yong2, JIN Mingliang2, LI Yinhong1

(1. State Key Laboratory of Advanced Electromagnetic Engineering and Technology (Huazhong University of Science and Technology), Wuhan 430074, China; 2. Central China Branch of State Grid Corporation of China, Wuhan 430077, China)

The smooth online setting of relay protection in a complex loop network depends on the fast calculation of the minimal break point set. However, the existing algorithm for this set has some shortcomings in algorithm complexity, dimension of breakpoint set and computational efficiency. An algorithm to calculate the minimal break point set for relay protection online setting is proposed. Based on the inherent relationship between basic cut set matrix and basic loop matrix in graph theory, the problem of finding the break point set of a complex loop network is transformed into that of finding the break point set of basic loop based on basic cut set matrix. The minimal break point set of the network is obtained by adjusting the basic cut set matrix dynamically. Example analysis shows that the proposed algorithm can obtain the minimal break point set of the network in an effective time, and this greatly reduces the complexity of the problem.

relay protection online setting; directional relay of loop network; minimal break point set; basic cut set matrix; fundamental loop matrix

10.19783/j.cnki.pspc.211312

国家重点研发计划项目资助(2016YFB0900100)

This work is supported by the National Key Research and Development Program of China (No. 2016YFB0900100).

2021-09-26；

2021-12-06

任康杰(1998—)，男，硕士研究生，主要研究方向为电力系统继电保护分析及整定计算；E-mail: renkangjie@ hust.edu.cn

刘 阳(1988—)，男，博士，高级工程师，研究方向为电力系统继电保护分析及整定计算；E-mail: liuyangwuh520@ sina.com

李 勇(1981—)，男，硕士，教授级高级工程师，主要研究方向为电力系统继电保护分析及整定计算。E-mail: 500ly@163.com

(编辑 魏小丽)