一种基于关联集和可用度的光伏发电系统维护策略
陈 伟,李旭斌,纪青春,裴喜平,王忠飞,何 峰
一种基于关联集和可用度的光伏发电系统维护策略
陈 伟1,李旭斌1,纪青春2,裴喜平1,王忠飞2,何 峰2
(1.兰州理工大学电气工程与信息工程学院,甘肃 兰州 730050;2.国网甘肃省电力公司兰州供电公司,甘肃 兰州 730050)
针对光伏发电系统定期维修费用较高且不能充分利用系统实时状态而动态调整维修策略的问题,在考虑设备运行状态和天气因素影响的基础上,提出了一种基于关联集和可用度的光伏发电系统动态组合维护策略。首先,从设备功能相关性出发建立关联集,以关联集为单位进行维修决策,并通过改进的马尔可夫模型预测设备和关联集状态,计算其可用度。然后,在设备维修决策阶段,以维修成本最低和可用度最高为目标,通过引入方式因子结合设备状态类型确定维修时间及方式。在关联集维修策略优化阶段,依据设备之间经济结构相关性建立共同维修决策集,从而确定系统最佳维修策略。最后,以某光伏电站为例验证了所提方法的正确性和有效性。结果表明,该方法能有效节省系统维修总费用,提高系统可用度。
相关性;关联集;状态预测;可用度;天气因素;维修策略
0 引言
光伏电站一般建立在光照充足的空旷区域,其运行环境复杂、运维费用昂贵、运维难度较大。因此,制定合理有效的运维策略对光伏电站安全、经济、稳定运行具有重要的意义。
光伏发电系统是光伏组件、汇流箱、逆变器和变压器等多部件组成的复杂系统。对于多部件复杂系统,事后单独维修已经不能满足维修可靠性要求,须考虑部件之间的耦合关联特性,进行预防性维修。文献[1-4]以可靠性为约束条件,通过更新维修阈值对部件进行预防性维修。文献[5]基于可靠性约束,建立马尔可夫状态检修模型,且验证了该模型可提高设备可用度。文献[6-7]提出了状态-机会维修策略,该策略作为预防性维修的一种典型形式被广泛应用到维修领域。文献[8]提出了一种基于可靠性的预防性检修模型。文献[9]以降低维修成本为目标,提出了针对机组部件的组合维修策略。文献[10]考虑部件之间的故障和经济相关性提出了上下层优化的预防性维护模型。文献[11]计及部件之间的功能关联性提出了状态检修决策模型。文献[12]通过相关矩阵建立部件之间的故障相关性,并通过考虑维修时间、经济相关性建立了机会维修模型。文献[13]通过对比不同故障组件串数对维修费用的影响,证明了维修时故障组件串占比越高,维修费用越高。文献[14]通过分析维修周期和维修费用的关系得出了维修周期越长,维修费用越低,可靠性越低的结论。当前维修领域还有基于状态监测及预测的维修,以维修费用最低或风险最小建立目标函数,确定维修时间和方式。文献[15]计及设备的老化过程,以维修费用最低和可靠度最大为目标,提出了不完全维修策略。文献[16]结合故障分析法及GO法对设备进行可靠性分析,建立了基于改进粒子群算法的维修优化模型。文献[17-21]通过马尔可夫状态转移方程描述设备劣化和故障演化过程,并以维修费用最低来确定维修方式和维修时间间隔。文献[22]采用蒙特卡洛来模拟影响设备状态劣化的随机不确定性因素和不同维护方式对状态恢复的影响,以单位时间运维成本最低为目标,确定最佳维修方式。文献[23]通过考虑设备相关性,以设备和系统风险之和最小为目标,构建了一种机会维修模型。文献[24]考虑特殊环境提出了一种预测性动态维护模型。文献[25]提出了一种考虑需求响应的多目标发电检修调度模型。文献[26]提出了元件-系统分级优化的光伏电站维护策略,通过计算维修时间阈值确定最优维修策略。文献[27-28]通过预测设备状态来确定维修时间间隔和维修周期。以上文献计及设备的状态转移过程,通过状态预测进行预测性维修,在一定程度上提高了维修效率。
上述研究对维修策略的确定主要基于设备的运行状态,分析设备可靠性来判断是否需要维修,然后在考虑维修费用的基础上优化维修策略。这种方法确定的维修方案可保证设备的可靠性,但未能综合考虑可用度和关联性的影响,在一定程度上减少了维护成本,却不能使系统可用度最高,从而不能保证光伏发电效率最大,因此所确定的维修方案不一定是系统的最佳维修方案。针对以上问题,本文首先通过分析光伏电站设备的功能相关性建立了维修关联集,并依据改进的马尔可夫模型确定设备和关联集可用度,然后在考虑天气参数、关联性和可用度对维修费用和维修策略影响的基础上,提出了一种基于关联集和可用度的光伏发电系统动态组合维护策略。结果表明,该策略能有效节省系统维修总费用、减少停机损失及提高系统可用度,从而增大光伏电站收益。
1 关联性分析
光伏系统各设备依功能相关性分解成不同的主从关联集,以关联集为单位进行维护决策。所谓关联集指系统中有功能相关的设备构成的集合,从光伏发电系统网络拓部结构来看,关联集包括光伏子阵列、汇流箱、逆变器和变压器等设备。
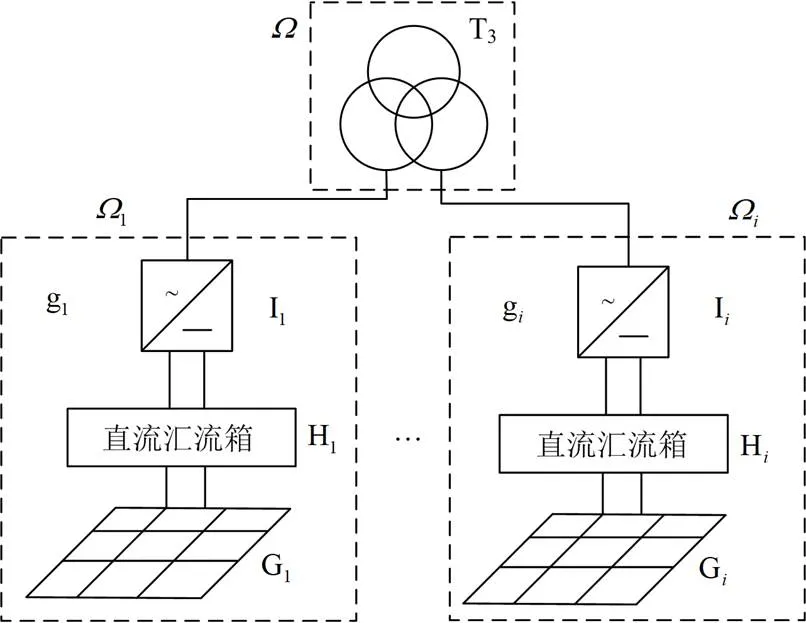
图1 关联集示意图
2 光伏发电系统各设备和关联集状态预测
光伏发电系统中变压器、逆变器、直流汇流箱和光伏阵列等在使用中均会发生老化,且在实际运行中同样存在突发性故障,这类故障通常由外部随机因素造成,会影响检修决策结果。
2.1 设备状态转移过程
依IEEE标准导则,电力设备的运行状态划分为正常、注意、异常和严重状态,一般而言,将严重状态作为故障处理。为综合考虑劣化故障及突发性故障,本文通过改进三阶老化马尔可夫模型[18]建立新的马尔可夫状态转移模型,描述设备的故障规律。
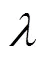
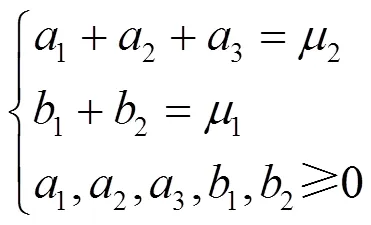
2.2 设备状态概率计算
若设备初始状态为0,依据2.1节分析得到设备马尔可夫状态转移率矩阵,如式(2)所示。
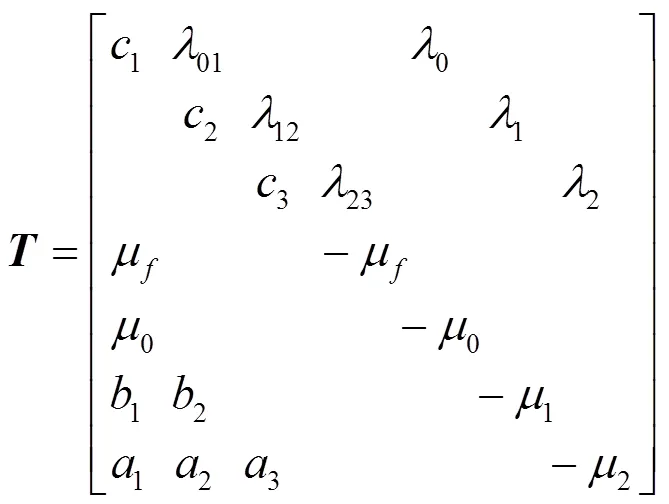
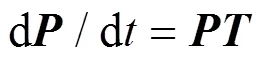
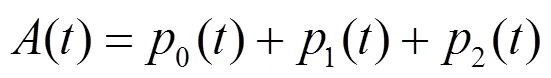
令设备修复率均为0,则设备初始状态正常时的首次寿命分布函数为
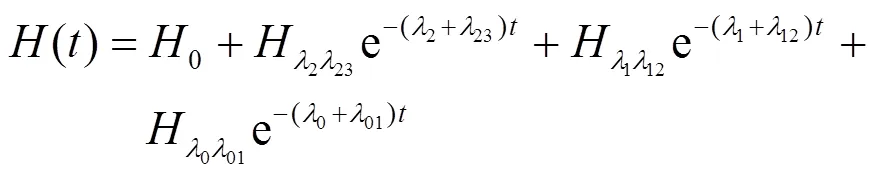
式(5)中系数可对照式(6)求得。
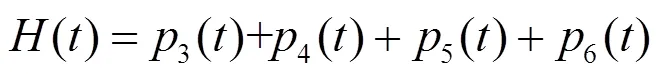
2.3 关联集状态概率计算
依据文献[11]所述方法求得该情况的可用度,如式(8)所示。
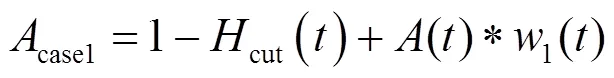

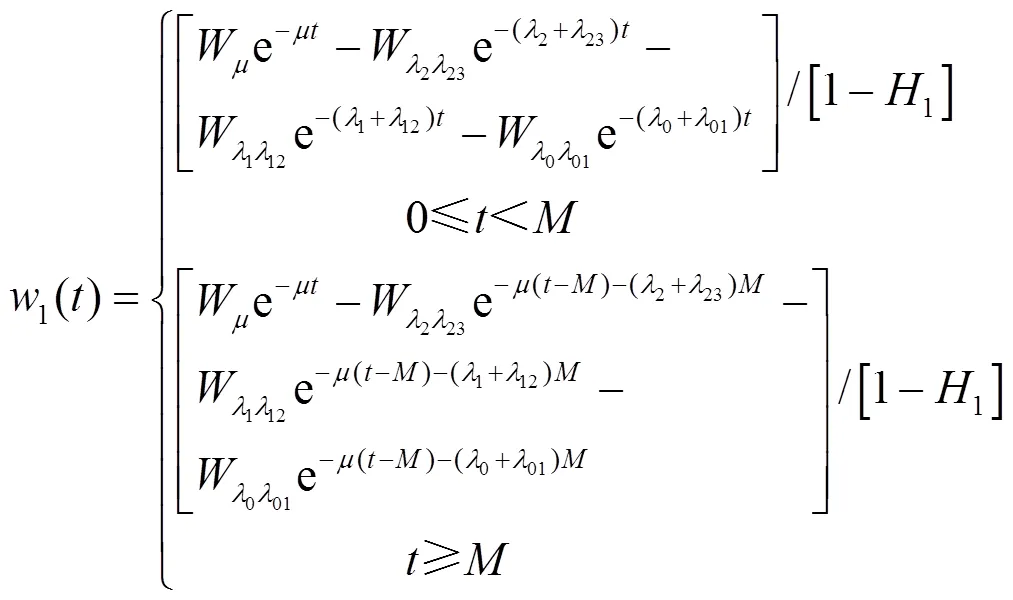
其中:
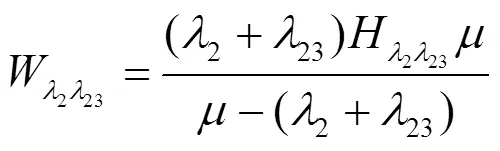

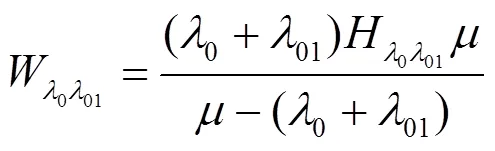
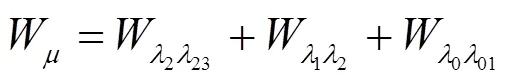
该情况发生的概率为
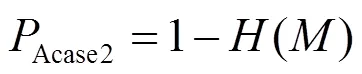
该情况的可用度为
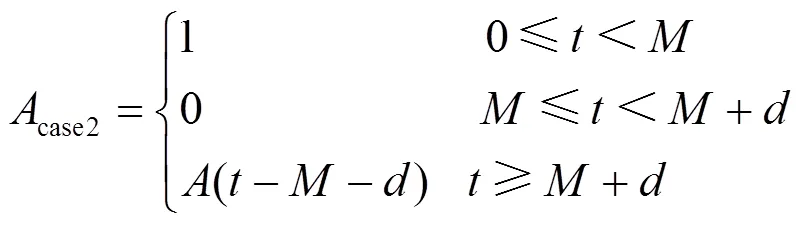
综合以上两种情况,总可用度为
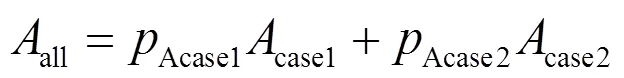

图3 关联集状态转移过程

由于关联集状态转移率为常数,故其转移可通过马尔可夫过程进行描述,则转移率矩阵为
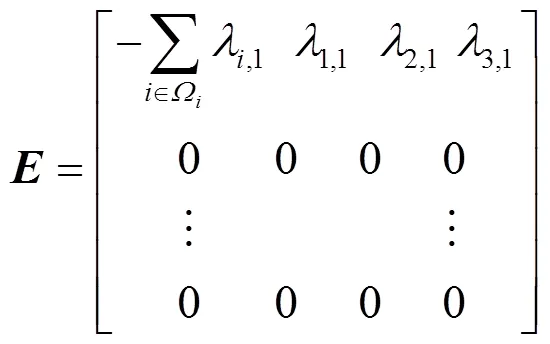
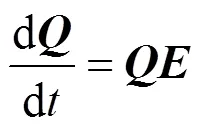

针对关联集在检修计划前是否发生故障,做如下分析。
(1) 关联集在检修计划前未发生停运
关联集可用度为
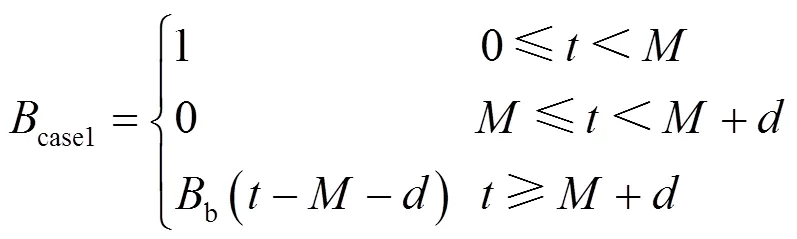
(2) 关联集在检修计划前因设备故障提前检修而停运
该情况发生时,关联集首次寿命分布为在式(21)基础上的截尾分布,其分布函数为
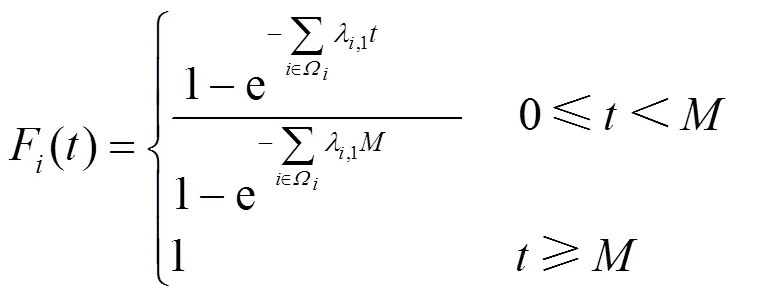
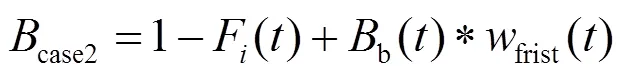
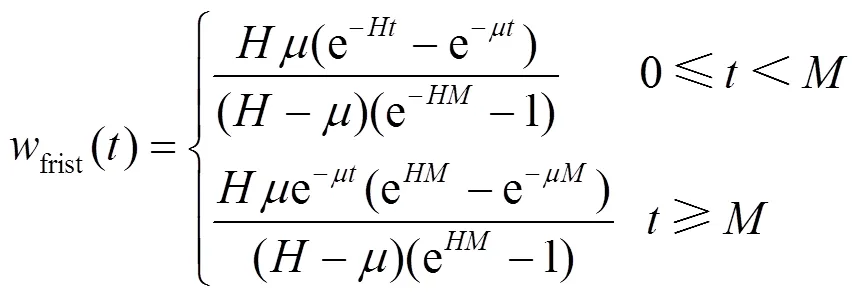
综合以上情况,通过结合式(17)可得关联集总可用度。
3 光伏发电系统组合维修策略
光伏发电系统以往的定期维修忽略关联性、可用度和天气因素对维修策略和维修费用的影响,将维修时间和周期设置为定值,维修费用较高,维修策略可待进一步优化。因此,本文以维修费用最低和可用度最大为目标,以可靠性、检修资源和检修时间限制为约束条件,提出新的光伏发电系统动态组合维护策略。
3.1 模型假设
本文在检修决策时做如下规定:
1) 当设备发生劣化故障无法修复时,对其进行更换,更换后系统中该设备功能状态“恢复正常”;
2) 当设备发生突发性故障时,立即对其停机检修,维修方式由设备的受损程度确定;
3) 各设备的故障分布相互独立;
4) 设备的修复时间服从指数分布。
3.2 模型思路分析
组合维护策略的基本思路如图4所示。
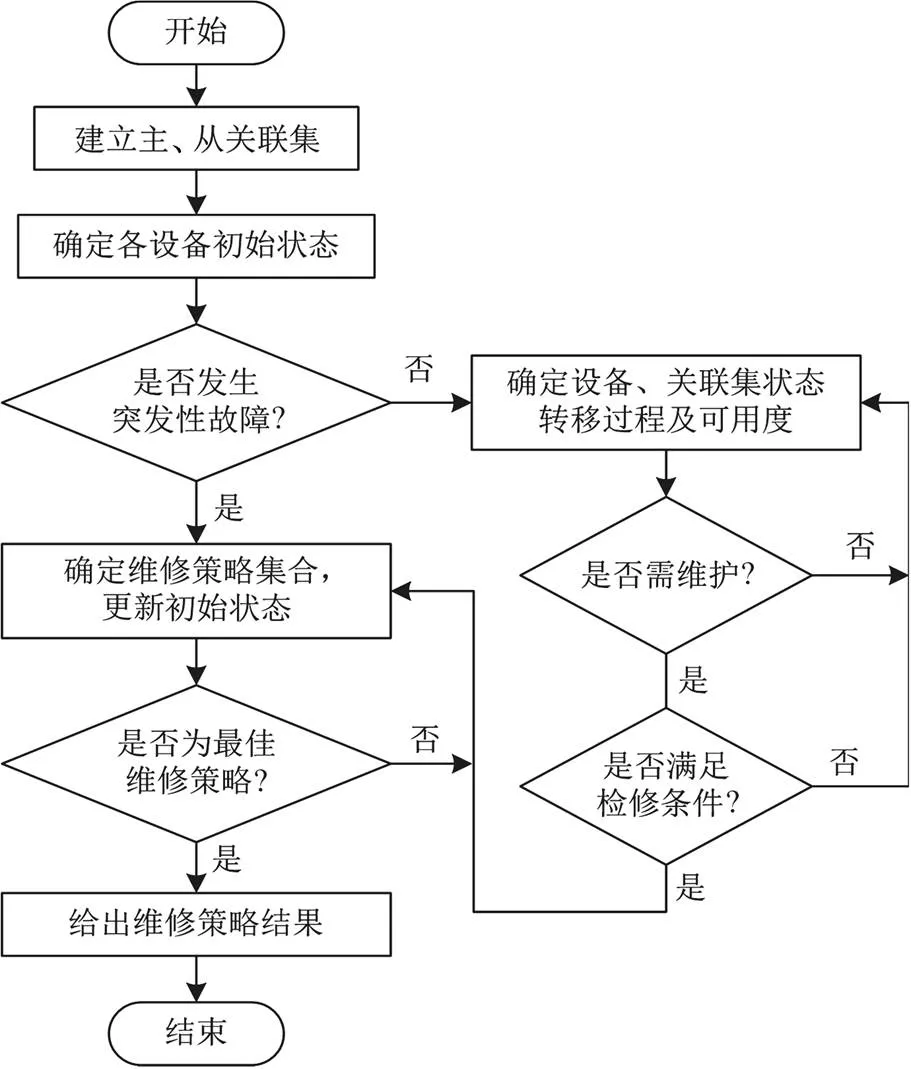
图4 组合维护策略基本思路
1) 采集光伏电站各设备相关数据,通过模糊综合研判等方法评估其初始状态类型;
2) 判断其是否需要维修,并结合机会维修思想,判断关联集内各设备是否需要共同维修;
3) 确定维修策略集合,以维修成本最低、可用度最大确定最优维修策略集合;
4) 依据初始状态预测各设备状态类型,根据预测结果确定系统最佳预防性维修策略。
维修策略集合确定思路如图5所示。
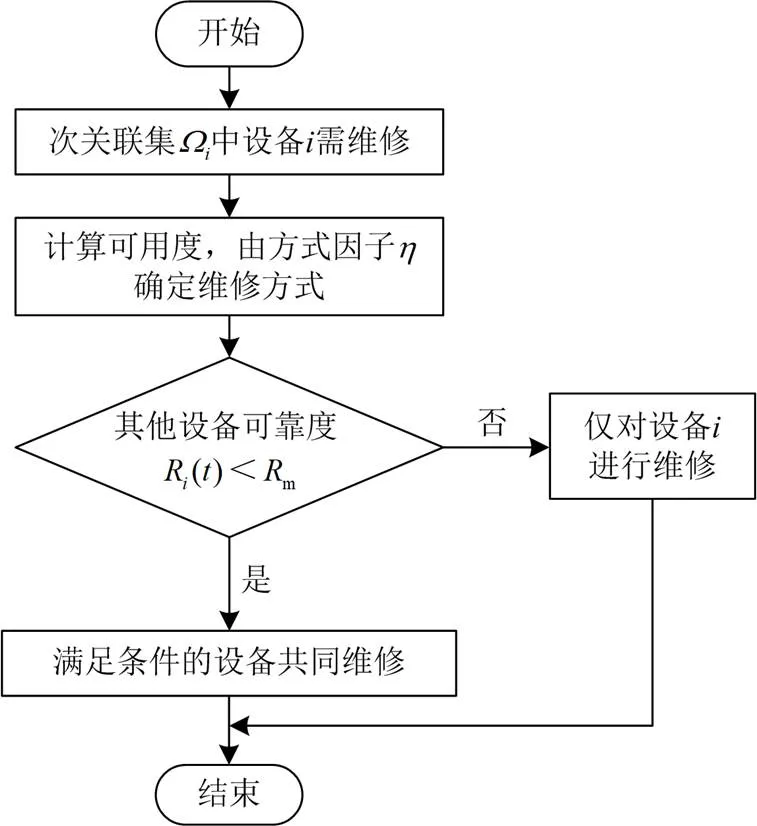
图5 维修策略集合确定思路
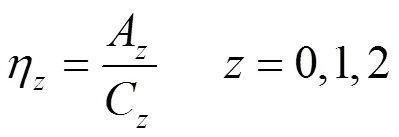
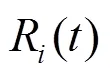
3.3 目标函数及约束条件
本文以维修费用最低,系统可用度最高建立目标函数,具体表达为
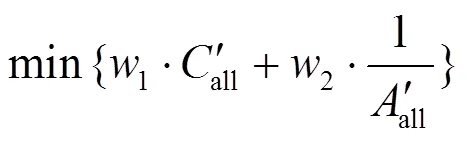
3.3.1维修费用分析
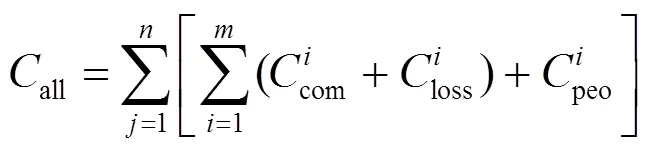
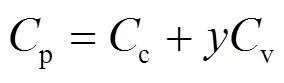
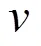
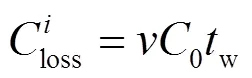
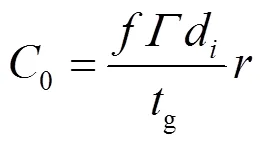
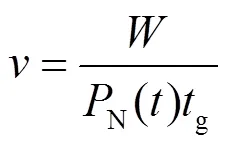
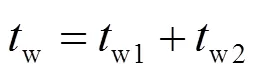
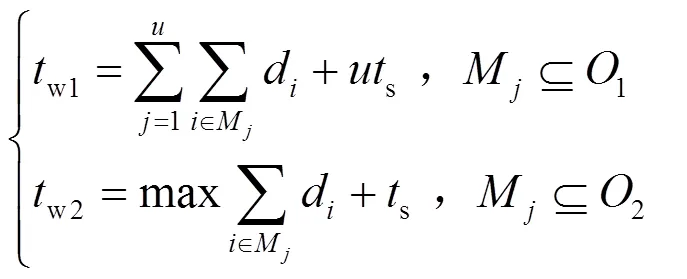

维修人员费用包括基本工资及奖金,如式(38)。

3.3.2可用度分析
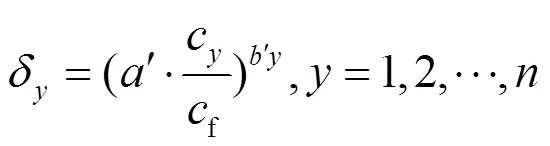
3.3.3设备进行检修时的约束条件
1) 可靠性约束
由于光伏设备在实际运行中受外部因素的影响,故障率呈动态增大趋势。因此,为使维修更符合工程实际,结合文献[29]所提出混合故障率模型来描述可靠度,即为

约束条件为

2) 检修资源约束
检修时段内,由于人力、所需材料等资源的限制而不能同时检修各个设备,需顺序进行,故有
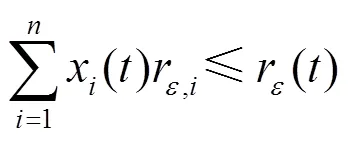
3) 检修时间约束
检修时间限制在可检修的时间段内,即

4 仿真分析
以某10 MW光伏电站中一个发电单元为例,通过对比两种方案验证该模型的经济有效性。
方案一:不考虑关联集和可用度的定期维修模型;方案二:考虑关联集和可用度的本文模型。

表1 不同维修方式费用
结合光伏电站所处环境及发电数据,绘制得到图6。通过图6及气象站数据统计计算,得到每个月天气可及率和容量因子,如图7所示。
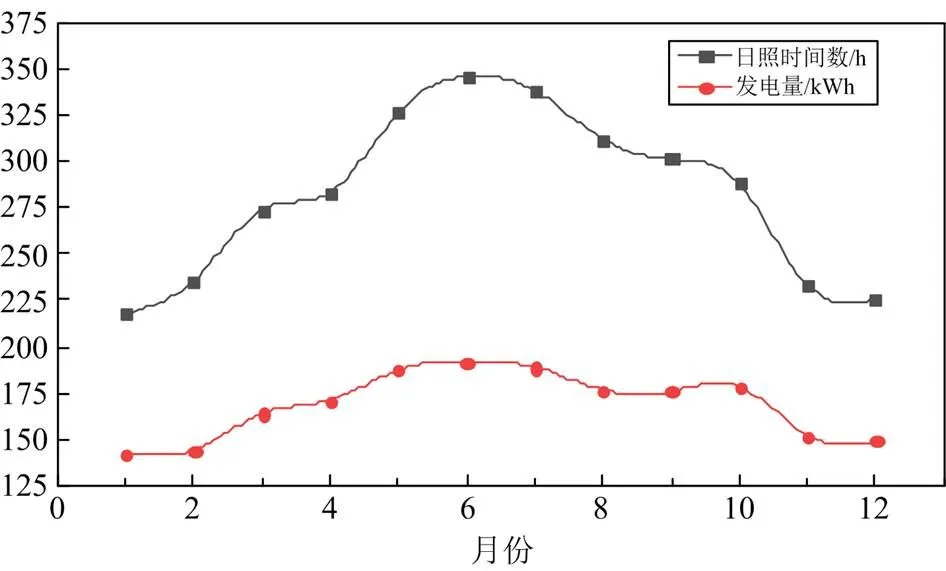
图6 光伏电站发电曲线
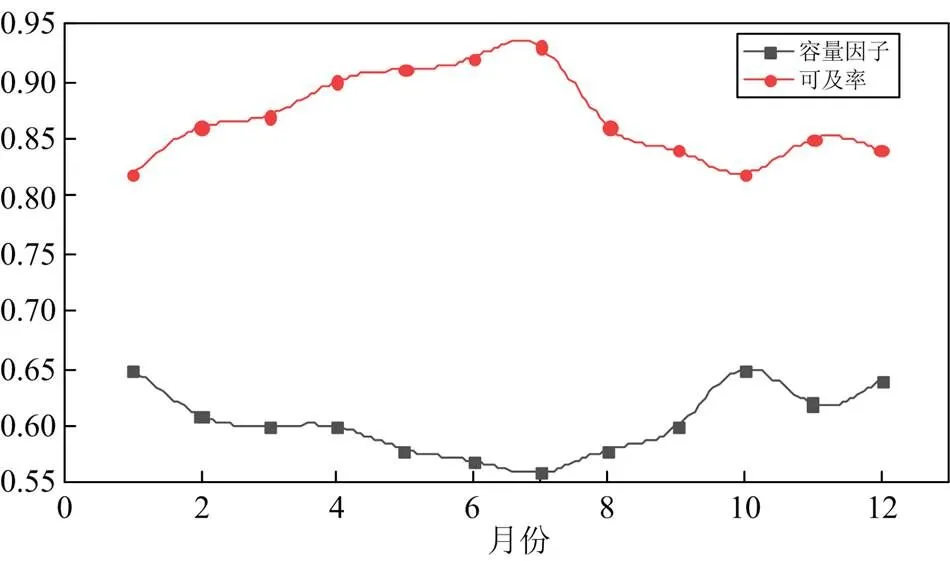
图7 天气参数
由图7可见,该地区4月至7月可及率较大,容量因子较小,故维护停机时间较短,维护停机损失较少,最适宜维护检修。受气候条件影响,第1、10和12月可及率较低,容量因子相对较大,不适宜外出检修。
4.1 设备性能分析
4.1.1定期维修模型设备性能分析
由图8、图9可见,设备各个状态概率趋于稳定值,且最终可用度为0.88。如果将可用度最大作为目标,则可通过改变维修方式比重得到最优维修策略,显然当设备发生故障时进行更换可得最大可用度,但不符合经济性的要求。
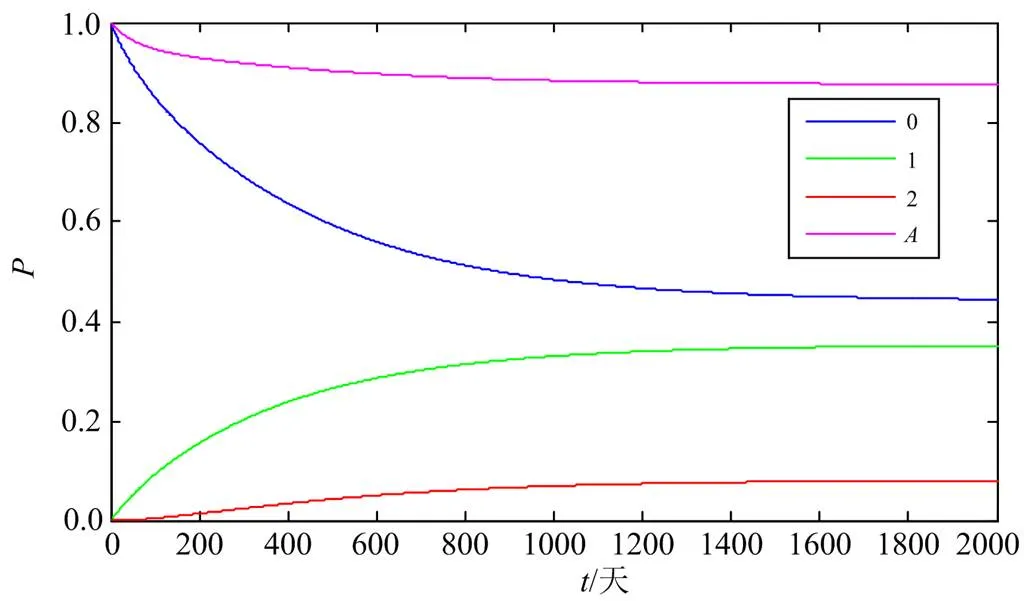
图8 状态0—2及可用度概率曲线
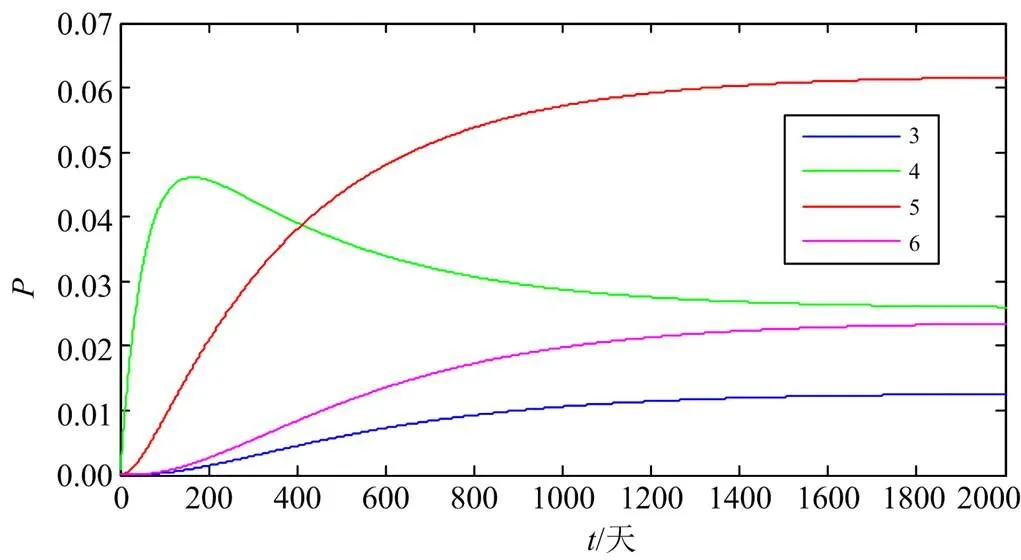
图9 状态3—6概率曲线
4.1.2两种维修模型设备性能对比
由图10可见:方案一不计及设备可用度的影响,通过一定比例的维修方式进行维修;方案二通过计算设备可用度,当其低于0.9时进行预防性维修,通过方式因子判断维修类型;由于马尔可夫链最终状态与状态转移率有关,而与初始状态无关,所以方案二长时间可用度稳态值与方案一一致。

图10 两种维修方式可用度
光伏阵列初始状态为0,依据文献[26]所提供的光伏阵列状态转移率,通过马尔可夫链进行状态预测,可得其可用度曲线,如图11所示。由图11可见,当其稳定运行到317天时,可用度降低到0.9。因此在该时刻前后需要安排维修。
两种维修方式的可用度曲线如图12所示,若维修按方案一进行,则其可用度变化曲线随时间缓慢下降,当到402天时达到0.9,此后一直以低于0.9的可用度运行到老化失效;若维修按方案二进行,则可用度随时间不断更新变化,保证其始终在0.9以上。
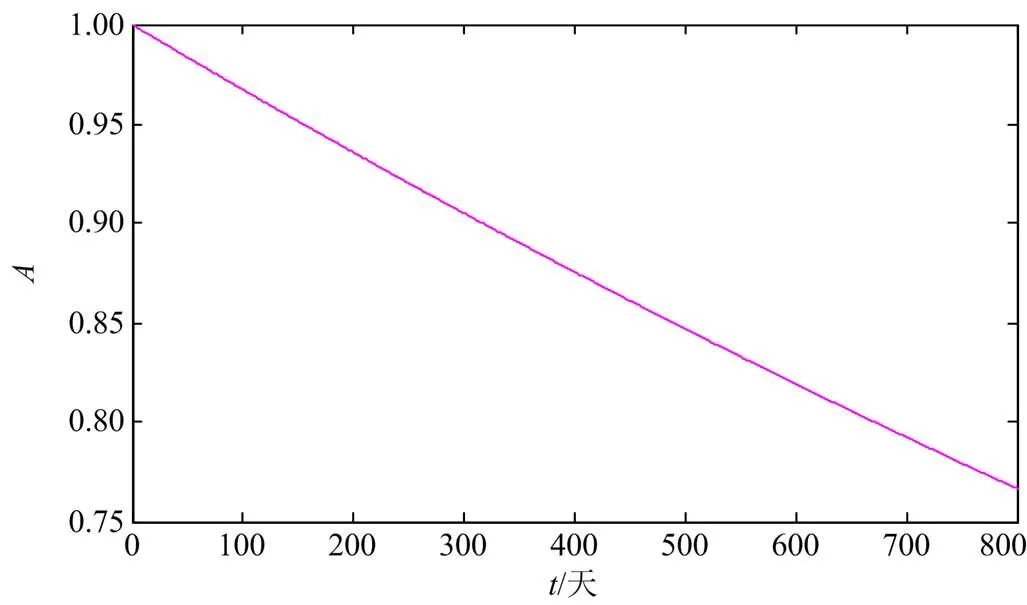
图11 光伏阵列可用度
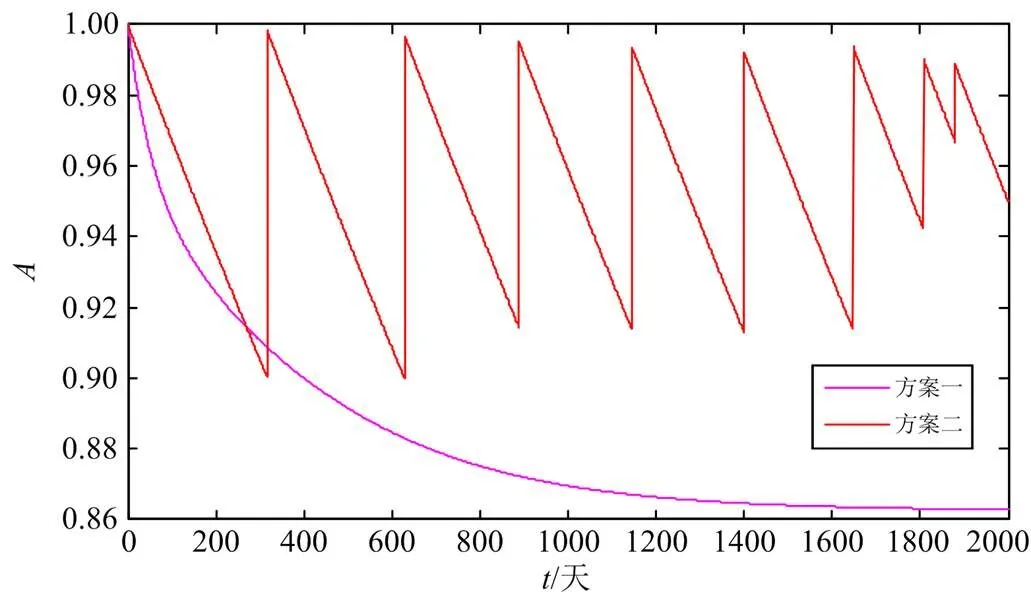
图12 光伏阵列可用度对比图
4.2 系统性能和经济性分析
4.2.1系统性能分析
图13为两种维修方案系统可用度对比图,图14为方案二维修后可用度。

图13 系统可用度
由图13可见,方案一系统可用度随时间从1降到0.65,整体可用度较低;结合图14可知,方案二每次维修后设备及系统可用度均大于0.9,呈现动态变化趋势,整体可用度较高。由此可见,方案二发电单元系统整体运行时间较长,停运时间较短,收益更大。

图14 方案二维修后可用度
4.2.2经济性分析
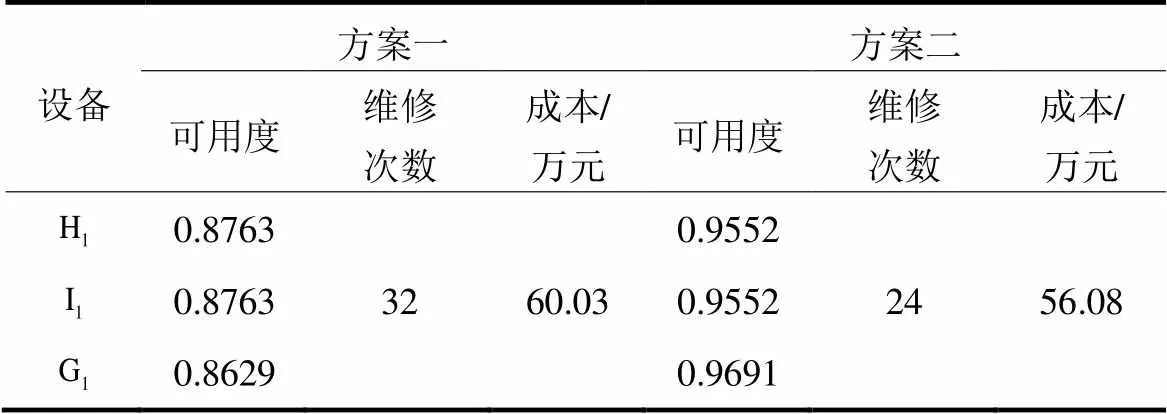
表2 两种方案仿真对比

表3 共同维修决策集
4.3 天气因素影响分析
4.3.1天气参数对维修费用的影响分析
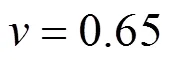

图15 维修费用曲线
由图15可知:当考虑天气可及率时,停机损失随停机时间的增加而增加,运维费用较高;当考虑容量因子时,停机损失减少,维修费用较低。由此可见,光伏电站发电单元在实际运行过程中,每次维修时间不同,天气可及率和容量因子不同,则在不同维修时间即使维修方式相同,维修费用却不一定相同。
4.3.2天气可及率对维修费用变化率的影响分析
通过定期维修模型和本文模型两种方案比较分析天气可及率对维修费用变化率的影响。维修费用随天气可及率的变化曲线如图16所示。
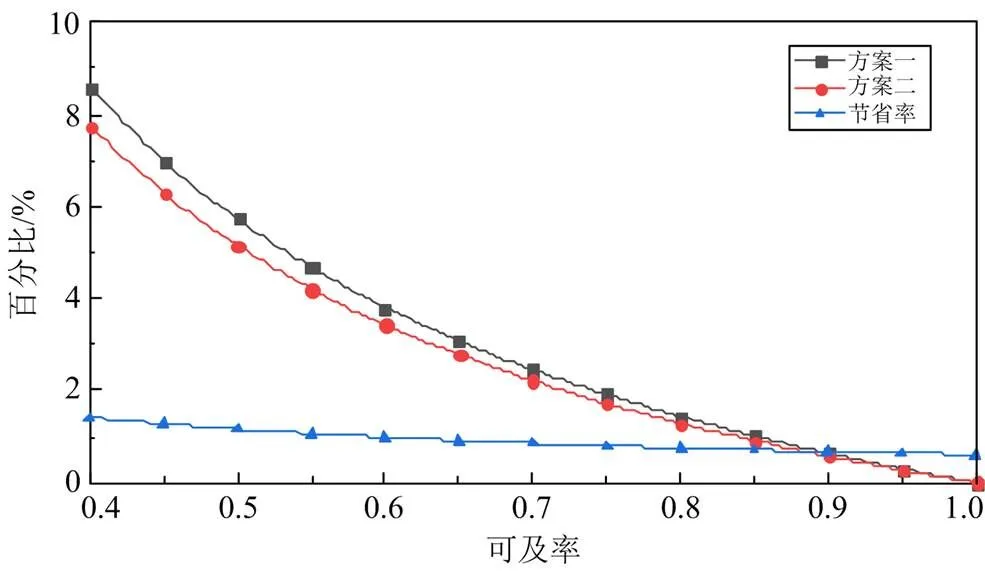
图16 维修费用变化率曲线
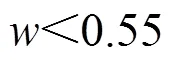
5 结论
本文提出了一种基于关联集和可用度的光伏发电系统动态组合维护策略,通过仿真分析得到以下结论:
1) 在设备维修决策阶段,基于改进的马尔可夫状态预测结果,通过引入维修方式因子,在保证可靠性的前提下得到了每个设备的最佳维修时间和维修方式,有效避免了过修或欠修。
2) 在系统维修策略优化阶段,计及设备的功能相关性建立了关联集,算例表明考虑关联集的维修策略能有效减少系统总的维修次数,降低维修总费用,提高可用度,增大光伏电站收益。
3) 考虑了天气可及率对维修费用的影响,通过对比定期维修策略,结果表明天气可及率越低该策略的维修费用节省率越大,从而验证了该策略在复杂环境的普适性。
本文在研究过程中未能考虑设备之间的失效相关性,天气参数对维修次数、可用度及维修方式的具体影响,将在下一步展开研究。
[1] 甘婕, 曾建潮, 张晓红. 考虑性能可靠度约束的维修决策模型[J]. 计算机集成制造系统, 2016, 22(4): 1079-1087.
GAN Jie, ZENG Jianchao, ZHANG Xiaohong. Maintenance decision model with performance reliability constraints[J]. Computer Integrated Manufacturing System, 2016, 22(4): 1079-1087.
[2] LE M D, TAN C M. Optimal maintenance strategy of deteriorating system under imperfect maintenance and inspection using mixed inspection scheduling[J]. Reliability Engineering & System Safety, 2013, 113(1): 21-29.
[3] DRIESSEN J P C, PENG H, VAN HOUTUM G J. Maintenance optimization under non-constant probabilities of imperfect inspections[J]. Reliability Engineering & System Safety, 2017, 165(9): 115-123.
[4] ROBERT A, NEAL D, ROBERT J. Equipment failure characteristics & RCM for optimizing maintenance cost[J]. IEEE Transactions on Industry Applications, 2015, 52(2): 1257-1264.
[5] 叶远波, 刘宏君, 黄太贵, 等. 变电站继电保护设备状态检修可靠性分析方法研究[J]. 电力系统保护与控制, 2021, 49(10): 170-177.
YE Yuanbo, LIU Hongjun, HUANG Taigui, et al. Research on the reliability analysis method of condition-based maintenance of relay protection equipment in substation[J]. Power System Protection and Control, 2021, 49(10): 170-177.
[6] 赵洪山, 张健平, 高夺, 等. 风电机组的状态–机会维修策略[J]. 中国电机工程学报, 2015, 35(15): 3851-3858.
ZHAO Hongshan, ZHANG Jianping, GAO Duo, et al. A condition based opportunistic maintenance strategy for wind turbine[J]. Proceedings of the CSEE, 2015, 35(15): 3851-3858.
[7] 赵洪山, 张健平, 程亮亮, 等. 考虑不完全维修的风电机组状态–机会维修策略[J]. 中国电机工程学报, 2016, 36(3): 701-708.
ZHAO Hongshan, ZHANG Jianping, CHENG Liangliang, et al. A condition based opportunistic maintenance strategy for wind turbine under imperfect maintenance[J]. Proceedings of the CSEE, 2016, 36(3): 701-708.
[8] 李生虎, 赵慧洁, 周慧敏, 等. 基于可靠性灵敏度的UHVDC系统预防性检修优化[J]. 电力系统保护与控制, 2022, 50(3): 68-75.
LI Shenghu, ZHAO Huijie, ZHOU Huimin, et al. Reliability sensitivity-based optimization for a UHVDC transmission system with preventive maintenance[J]. Power System Protection and Control, 2022, 50(3): 68-75.
[9] 赵洪山, 李自立, 刘宏杨, 等. 风电场的组合维修策略研究[J]. 太阳能学报, 2021, 42(2): 189-196.
ZHAO Hongshan, LI Zili, LIU Hongyang, et al. Research on combination maintenance strategy of wind farms[J]. Acta Energiae Solaris Sinica, 2021, 42(2): 189-196.
[10] 符杨, 杨凡, 刘璐洁, 等. 考虑部件相关性的海上风电机组预防性维护策略[J]. 电网技术, 2019, 43(11): 4057-4063.
FU Yang, YANG Fan, LIU Lujie, et al. Preventive maintenance strategy for offshore wind turbines considering component correlation[J]. Power System Technology, 2019, 43(11): 4057-4063.
[11] 徐波, 韩学山, 刘长银, 等. 基于关联集分解的系统状态检修决策模型[J]. 电力系统自动化, 2015, 39(2): 46-52, 86.
XU Bo, HAN Xueshan, LIU Changyin, et al. Condition- based maintenance decision-making model for power system based on association sets decomposition[J]. Automation of Electric Power Systems, 2015, 39(2): 46-52, 86.
[12] 杨元, 黎放, 侯重远, 等. 基于相关性的多部件系统机会成组维修优化[J]. 计算机集成制造系统, 2012, 18(4): 827-832.
YANG Yuan, LI Fang, HOU Chongyuan, et al. Opportunistic group maintenance optimization of multi-component system under dependence[J]. Computer Integrated Manufacturing System, 2012, 18(4): 827-832.
[13] 赵洪山, 张兴科, 郭伟. 考虑不完全维修的风机齿轮箱优化检修策略[J]. 电力系统保护与控制, 2014,42(10): 15-22.
ZHAO Hongshan, ZHANG Xingke, GUO Wei. Optimized maintenance strategy with imperfect repair for the gearbox of wind turbine[J]. Power System Protection and Control, 2014, 42(10): 15-22.
[14] DHOPLE S V, DOMINGUEZ-GARCIA A D. Estimation of photovoltaic system reliability and performance metrics[J]. IEEE Transactions on Power Systems, 2012, 27(1): 554-563.
[15] PERDUE M, GOTTSCHALG R. Energy yields of small grid connected photovoltaic system: effects of component reliability and maintenance[J]. IET Renewable Power Generation, 2015, 9(5): 432-437.
[16] 刘欢, 刘志刚. 基于改进粒子群算法的牵引变电所维修优化研究[J]. 电力系统保护与控制, 2015, 43(11): 87-94.
LIU Huan, LIU Zhigang. An improved particle swarm algorithm study on optimization model of maintenance schedules for railway traction substations[J]. Power System Protection and Control, 2015, 43(11): 87-94.
[17] 刘璐洁, 符杨, 马世伟, 等. 基于运行状态监测与预测的海上风机维护策略[J]. 电网技术, 2015, 39(11): 3292-3297.
LIU Lujie, FU Yang, MA Shiwei, et al. Maintenance strategy for offshore wind turbine based on condition monitoring and prediction[J]. Power System Technology, 2015, 39(11): 3292-3297.
[18] 汲国强, 吴文传, 张伯明, 等.一种适用于状态检修的电力设备时变停运模型[J]. 中国电机工程学报, 2013, 33(25): 139-146, 21.
JI Guoqiang, WU Wenchuan, ZHANG Boming, et al. A time-varying component outage model for power system condition-based maintenance[J]. Proceedings of the CSEE, 2013, 33(25): 139-146, 21.
[19] BYON E, DING Y. Season-dependent condition based maintenance for a wind turbine using a partially observed Markov decision process[J]. IEEE Transactions on Power Systems, 2010, 25(4): 1823-1834.
[20] BYON E, NTAIMO L, DING Y. Optimal maintenance strategies for wind turbine systems under stochastic weather conditions[J]. IEEE Transactions on Reliability, 2010, 59(2): 393-404.
[21] OPREA S V, BARA A, PREOTESCU D, et al. Photovoltaic power plants (pv-pp) reliability indicators for improving operation and maintenance activities: a case study of PV-PP agigea located in Romania[J]. IEEE Access, 2019, 7: 39142-39157.
[22] SØRENSEN J D. Framework for risk-based planning of operation and maintenance for offshore wind turbines[J]. Wind Energy, 2009, 12(5): 493-506.
[23] 徐波, 韩学山, 李业勇, 等. 电力设备机会维修决策模型[J]. 中国电机工程学报, 2016, 36(23): 6379-6388, 6603.
XU Bo, HAN Xueshan, LI Yeyong, et al. Opportunistic maintenance decision-making model for power equipment[J]. Proceedings of the CSEE, 2016, 36(23): 6379-6388, 6603.
[24] MAKINDE O A, MPOFU K, RAMATSETSE B I, et al. A maintenance system model for optimal reconfigurable vibrating screen management[J]. Journal of Industrial Engineering International, 2018, 14(2): 521-535.
[25]俞晨玺, 孔维禄, 俞柏红, 等. 考虑需求响应的多目标机组检修调度优化[J]. 电力系统保护与控制, 2020, 48(11): 110-118.
YU Chenxi, KONG Weilu, YU Bohong, et al. Multi-objective optimization of generation maintenance scheduling considering demand response[J]. Power System Protection and Control, 2020, 48(11): 110-118.
[26] 朱晓荣, 刘亚维. 基于元件-系统分级优化的光伏电站维护策略[J]. 电力系统自动化, 2020, 44(8): 92-99.
ZHU Xiaorong, LIU Yawei. Maintenance strategy of photovoltaic power station based on component-system classification optimization[J]. Automation of Electric Power Systems, 2020, 44(8): 92-99.
[27] VERBERT K, SCHUT TER B D, BABUŠKA R. Timely condition-based maintenance planning for multi-component systems[J]. Reliability Engineering & System Safety, 2017, 159(10): 310-321.
[28] NGUYEN K A, DO P, GRALL A. Condition based maintenance for multi-component systems using importance measure and predictive information[J]. International Journal of Systems Science Operations & Logistics, 2014, 1(4): 228-245.
[29]李建华, 徐家生, 任丽娜. 可靠度约束下的不完全预防更换维修模型[J/OL]. 太阳能学报: 1-7[2021-05-27]. https://doi.org/10.19912/j.0254-0096.tynxb.2020-1372.
LI Jianhua, XU Jiasheng, REN Lina. Imperfect preventive replacement and maintenance model under reliability constraints[J/OL]. Acta Energiae Solaris Sinica: 1-7 [2021-05-27]. https://doi.org/10.19912/j.0254-0096.tynxb. 2020-1372.
A maintenance strategy for a photovoltaic power generation system based on an associative set and availability
CHEN Wei1, LI Xubin1, JI Qingchun2, PEIXiping1, WANG Zhongfei2, HE Feng2
(1. College of Electrical Engineering and Information Engineering, Lanzhou University of Technology,Lanzhou730050, China; 2. Lanzhou Power Supply Company,State Grid Gansu Electric Power Company,Lanzhou730050, China)
There is a problem in that the periodic maintenance cost is high in a photovoltaic system and cannot make full use of the real-time state of the system to dynamically adjust the maintenance strategy. Thus a new dynamically combined maintenance strategy for a photovoltaic system based on associative set and availability is proposed by considering the influence of equipment operational status and weather factors. First, the associative set between the equipment from the functional correlation is established and used to make maintenance decisions. Then the status of equipment and the associative set is predicted through an improved Markov model and their availability is calculated. Secondly, in the stage of equipment maintenance decision-making, the lowest maintenance cost and the highest availability are the goals. The maintenance time and mode of equipment is determined by the mode factor and the equipment status.In the optimization stage of associative set maintenance strategy, a joint maintenance decision set based on the economic and structural correlation of equipments is established and the best maintenance strategy for the system is determined. Finally, a photovoltaic power station is taken as an example to verify the correctness and effectiveness of the proposed method. The results show that this method can effectively save on the total cost of system maintenance and improve the availability of the system.
correlation;associative set; state prediction; availability; weather factor; maintenance strategy
10.19783/j.cnki.pspc.211275
国家自然科学基金项目资助(51767017);甘肃省基础研究创新群体项目资助(18JR3RA133)
This work is supported by the National Natural Science Foundation of China (No. 51767017).
2021-09-16;
2021-11-19
陈 伟(1976—),男,教授,博士生导师, 研究方向为新能源发电与综合能源利用;E-mail: chenlin@1ut.cn
李旭斌(1995—),男,通信作者,硕士,研究方向为新能源发电与综合能源利用。E-mail: 1469786076@qq.com
(编辑 姜新丽)

