基于多粒度特征选择和模型融合的复合电能质量扰动分类特征优化
阮梓航,肖先勇,胡文曦,郑子萱,汪 颖
基于多粒度特征选择和模型融合的复合电能质量扰动分类特征优化
阮梓航,肖先勇,胡文曦,郑子萱,汪 颖
(四川大学电气工程学院,四川 成都 610065)
现代电力系统因其“双高”特性造成电能质量扰动模式愈加复杂,对复合扰动的准确分类提出了挑战。传统电能质量扰动分类方法在特征提取阶段所提取的特征由人为确定,难以判断所提取的特征对分类问题是否有效,加之多重复合扰动特征相互耦合导致扰动特征的可分性确定困难。为此,提出一种基于粒度的计算方法进行特征选择的模型。在提取的扰动特征集的基础上,通过构建多粒度空间反映特征分布差异性,进而挖掘各粒度下的最优特征子集以确定有效和冗余的分类特征,达到优化分类效果的目的。在此基础上,通过集成分类模型融合不同粒度空间最优扰动特征集所训练的同质弱分类器模型,提出一种新的电能质量扰动多粒度集成分类方法。该方法克服了现有方法在进行多粒度分类时通过寻找最优单粒度空间特征而导致的其他粒度空间信息丢失的问题。实验表明,多粒度特征选择算法可提取对分类有效的扰动特征,集成分类模型可进一步改善模型的分类性能。
电能质量;复合扰动;特征选择;多粒度空间;集成分类
0 引言
随着电网分布式电源与电力电子装置比例升高,“双高”电力系统中电能质量扰动(Power Quality Disturbance, PQD)事件呈现频率高、模式复杂等特点[1-3]。如何准确辨识单一扰动构成的复合PQD事件,是实现复杂扰动源追溯和治理的必要前提。
现有复合PQD分类方法主要采用机器学习方法。文献[4-5]利用基于卷积神经网络的深度学习方法实现了电能质量的复合扰动分类,具有良好的学习和拟合能力,但该类方法训练时过度依赖数据导致模型计算量大、结构复杂,在训练样本数量较少的情况下学习能力不佳,而通过长期监测记录到的复合电能质量扰动事件数量远不足以满足深度学习的数据体量要求。其他机器学习方法在多数情况下可保证较好的学习和拟合能力,且在电能质量扰动分类领域广泛应用。例如,文献[6]设计了一种自适应滤波器来提取失真信号频域中的单频分量特征,改进了经验小波变换的特征提取效果;文献[7-9]分别利用变分分解、变频窗函数以及布莱克曼窗使S变换获得了更好的时频域分析能力。这些方法大多未考虑所提取的特征本身对分类性能的影响,冗余的特征会大量占用计算机资源并降低模型的分类性能,因此需要对提取的特征进行特征选择,现在针对PQD扰动的特征选择的方法已有研究[10-11],但对多标签数据集不同样本间特征分布的差异性以及类域的交叉重叠等模糊性、不确定性以及不完整问题对特征选择效果的影响考虑较少。因此,在特征选择阶段利用粒度计算的原理通过将类域转换为不同的知识粒度,并从不同知识粒度的角度观察和分析同一问题的影响,可了解不同粒度空间下特征对扰动类别可分性的不同贡献程度,以此作为判别特征好坏的依据[12-16]。
粒度计算所面临的多粒度空间特征最优子集挖掘决定了后续分类器设计同样要求在多个粒度空间中构建,传统的基于粒度计算的分类方法[15]大多是基于最优粒度空间的选择,但该类方法会丢失其他粒度空间的有用信息,因此需要对每个粒度空间进行融合。在现有模型融合方法中,Bagging模型采用投票或取平均值的方式集成多个同质弱学习器的分类结果,可降低分类模型的方差水平,提高鲁棒性[17];Boosting模型通常对多个同质弱学习器进行顺序拟合,着重于对分类性能较弱的基分类模型进行加权组合,可降低分类模型的偏置水平,提升准确率[18],但面临过拟合的问题。Stacking集成分类模型可突出分类性能优秀的基分类器模型,并采用非线性组合优化的方法进一步降低偏置水平,提升模型的泛化能力,使其具有更好的模型融合效果[19],但传统Stacking模型仅在相同特征维度下基于异质弱分类器组合优化以实现集成分类[20],不适用于本文多粒度空间中样本特征维度不同的情况下的组合优化。
为解决上述问题,本文提出一种基于多粒度空间的特征选择算法。该方法通过构建不同粒度特征空间反映特征分布的差异性,进而为特征选择提供决策依据,得到各粒度空间下的最优扰动特征集,实现特征选择。在此基础上,考虑融合各粒度空间各自的分类模型,提出电能质量扰动多粒度集成分类方法。该模型适用于在训练样本较小的情况下,利用基于粒度计算的特征选择算法和模型融合方法对机器学习模型的分类效果进行优化,并通过实验验证了本文方法的准确性与可靠性。
1 复合电能质量扰动的特点及特征提取
PQD扰动并不总是单一扰动,也可能出现多种单一扰动同时存在的情况,即复合扰动。受篇幅所限,本文以电网中常见的各类PQD扰动类型为分析对象,具体包含电压暂降(C1)、电压暂升(C2)、暂态振荡(C3)、谐波(C4)、电压中断(C5)、电压闪变(C6) 6种单一扰动模型,7种双重复合扰动模型和3种三重复合扰动模型,共16种单一和复合扰动模型。
由于本文方法需要对初始特征进行优化,因此在初始特征提取阶段,可不依赖专家经验,提取尽可能多的常见初始特征。本文对各类扰动信号采用S变换[21-22],分别得到时域最大值(max)、最小值(min)、平均值(mean)、标准差(std)、方均根值曲线(rms)和频域最大值(max)、最小值(min)、平均值(mean)、标准差(std)、方均根值曲线(rms);由于Hilbert边际谱曲线具有更高的频域分辨率,本文采用希尔伯特黄变换[23]获取扰动信号的Hilbert边际谱曲线(HMS)共11种PQD扰动特征曲线,再从上述11种特征曲线中提取出以下7类特征参数。
1)1—5分别为时频域特征曲线的最大值、最小值、平均值、标准差和均方根值,以反映基频扰动的幅值变化程度,可有效区分为暂升、暂降、中断、电压波动等扰动类型。2)6为频域特征曲线频率大于100 Hz频段的标准差,通过描述扰动特征在高频段数据与均值的偏离程度以衡量是否发生幅值波动,可有效区分谐波和振荡扰动类型。3)7为总谐波畸变率,即谐波与基波均方根值之比,对谐波扰动类型具有较高的区分度。
综上,本文构建60维时频域特征作为初始特征集合,如表1所示。需要说明的是,该集合仅是根据常见特征构造而来,实际应用中可提取更多特征,且冗余特征会在优化过程中被删除而不会造成分类性能下降。由于本文主要针对特征优化,特征提取方法不是本文的研究工作,其详细计算流程不再赘述,各参数的计算过程见相关文献[1,18,24-25]。

表1 PQD时频域特征
2 多粒度特征空间下多标签特征选择方法
2.1 变精度模糊邻域粗糙集的基本原理
针对复合PQD的高维特征集合,本节基于粗糙集的属性约简的粒度计算方法实现多粒度特征空间下的特征优化。一个多标签决策系统(Multi-Label Decision System, MLDS)如式(1)所示。
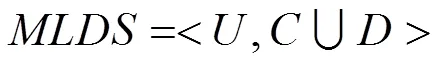
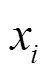



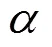
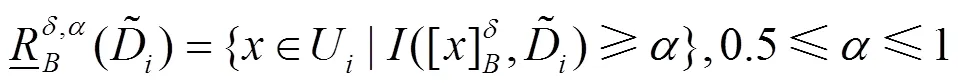
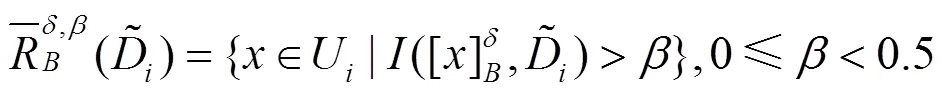

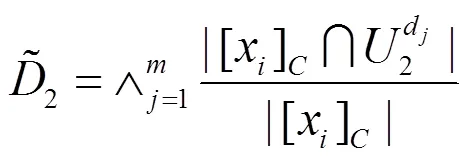

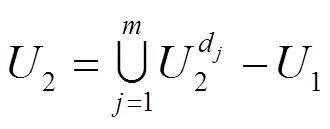

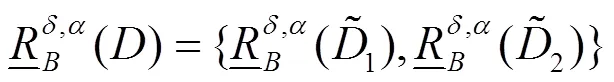

对于所有∈,标签集合对条件属性集合的依赖度的计算公式如式(12)所示。
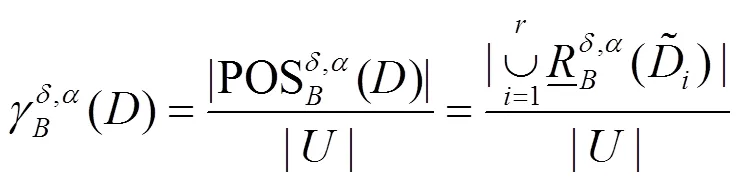
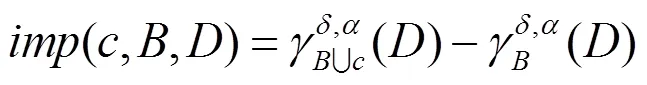
从而将重要度大于某一阈值的特征作为该粒度空间下的按特征重要度排序的最优特征子集。
2.2 考虑多粒度特征空间分布差异的特征选择算法

6) 根据式(4)—式(12)计算多标签扰动特征集相对于扰动标签的依赖度;
3 基于模型融合的复合电能质量扰动集成分类
3.1 Stacking集成分类的基本原理
由于本文的特征选择算法在不同粒度空间下生成的最优特征子集仅对某些PQD扰动类型具有较好的表征能力,为了获取对全样本空间的PQD扰动的识别能力,采用基于同质弱分类器不同特征维度的Stacking集成分类模型。模型融合是通过特定方式将多个不同的基分类器模型进行组合,得到多模型的综合分类系统,以提升分类模型的性能,Stacking模型融合是一种分层的模型集成策略,既能有效提高模型分类性能,又不会导致模型过拟合。算法流程如图1所示。

图1 Stacking集成分类器模型
1) 对所有同质基分类器进行折交叉验证,将训练集划分为份,分别利用其中种不同组合的-1份训练集对基分类器进行训练,再利用与训练集对应的第折训练集D以及测试集进行测试,得到各基分类器模型的第折训练集D与测试集的预测结果。
2) 将各基分类器模型的第折训练集D的预测结果组合作为元分类器模型的新训练集输入,将各基分类器模型的测试集的预测结果相加并求平均值作为元分类器模型的新测试集输入,得到最终融合分类器模型,并用于分类测试。
不同的基分类器模型具有不同的误差特性,Stacking模型融合的目的在于弱化单个基分类器模型的误差特性对整个集成分类模型分类性能的影响,以提高多模型融合分类系统的分类性能。
3.2 基于模型融合的复合电能质量扰动分类辨识
XGboost是一种基于Boosting思想的集成树模型,通过不断对上一轮迭代的残差进行拟合,将多个弱分类器模型融合为一个集成的强分类器模型[26],相对传统方法在具有更好分类效果的同时,也具有更强的抗过拟合能力。因此本文选择XGboost作为分类器模型。XGboost第轮迭代生成的集成树模型如式(14)所示。
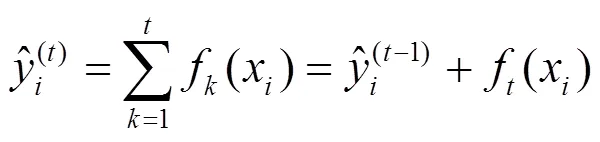

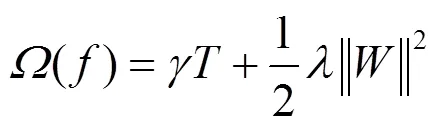



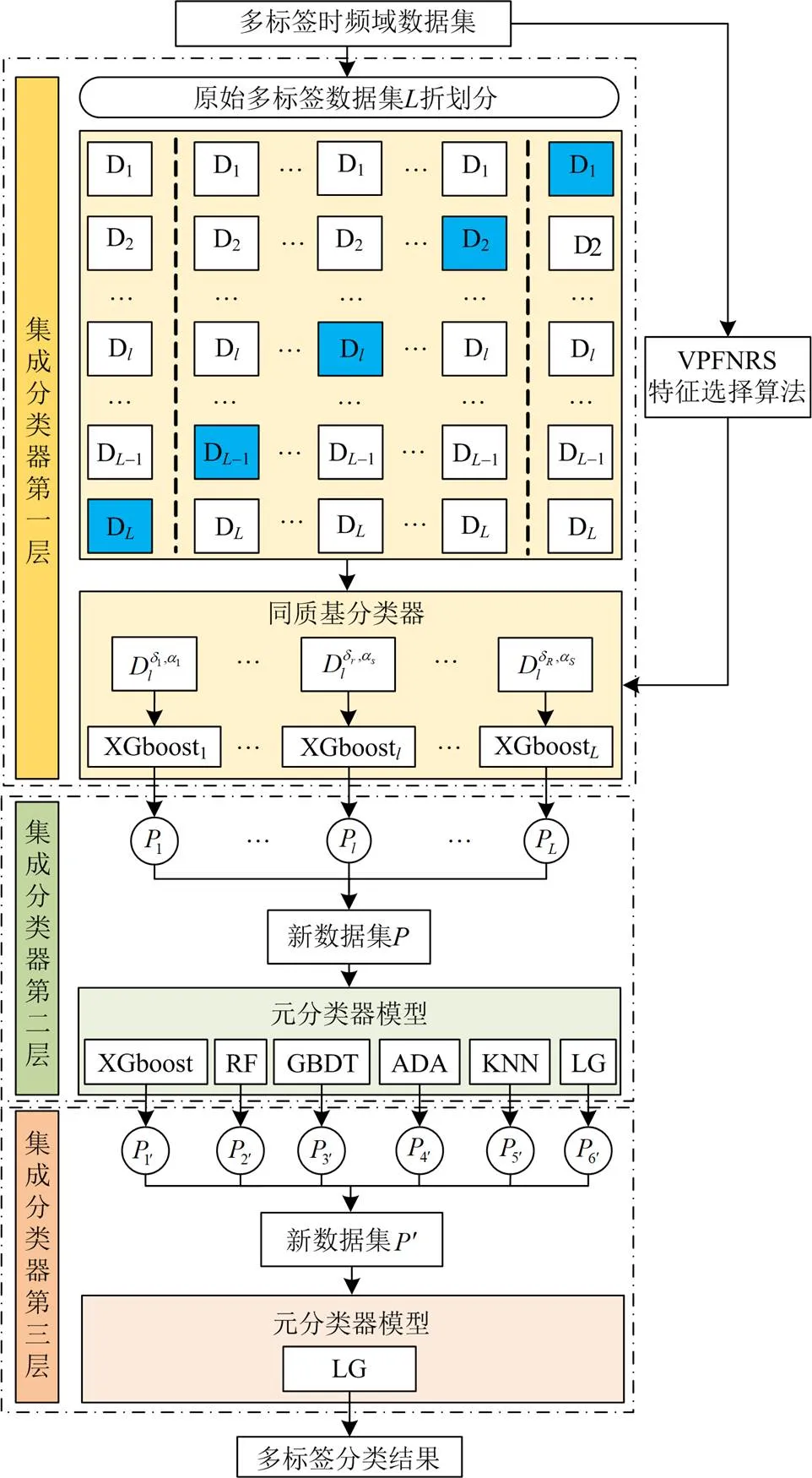
图2 VPFNRS-Stacking多粒度集成分类器模型
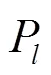
4 实验分析
本文分别采用仿真生成数据与电网实测数据进行验证,仿真生成数据参照文献[1]的方法以及IEEE标准[26],其中包含电网中常见的16类单一和复合扰动模型,扰动模型均采用归一化幅值曲线。每类扰动生成100个样本,其中50个作为训练样本,50个作为测试样本。为了验证模型的抗噪性能,对每类扰动信号添加30 dB、40 dB、50 dB高斯白噪声,作抗噪性能对比实验。信号基波频率为50 Hz,采样频率为6.4 kHz,采样周期为24个周期(0.48 s)。电网实测数据共包括24个样本。本文对特征选择和分类模型均采用如下评价指标:平均分类准确率(Average Precision, AP)、汉明损失(Hamming Loss, HL)、一类错误(One-error, OE)、覆盖率(Coverage, C)、排位损失(Ranking Loss, RL)和召回率(Recall, R),其中模型的汉明损失、一类错误、覆盖率、排位损失越小说明模型的分类能力越强。
4.1 时频域扰动特征量的提取
本文利用Matlab仿真16种单一和复合扰动的PQD扰动模型,对各类扰动模型分别采用S变换和希尔伯特黄变换,根据第1节的方法提取出11种时频域扰动特征曲线,以电压闪变+谐波双重复合PQD扰动为例,扰动信号的时频域特征曲线如图3中(b)和(c)所示。
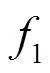
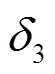


图4 不同分类方法下的时频域特征散点图
4.2 特征选择实验

图5 各粒度空间下扰动分类性能变化(30 dB)

图6 各粒度空间下扰动分类性能变化(50 dB)
由图5和图6可以看出,不同粒度空间对不同类别扰动的分类性能具有显著差异性,扰动在部分粒度空间下分类性能可达95%以上。在加入50 dB高斯白噪声后,部分粒度空间的分类准确率仍然能够保持在95%以上,证明该特征选择算法选择的特征是有效的,且对含噪声数据具有一定的耐受能力。不同粒度空间对应的最优特征集所构建的分类器模型具有不同的分类表现。
本节对VPFNRS-stacking、VPFNRS最优粒度模型、随机森林(Random Forest, RF)、递归特征消除(Recursive Feature Elimination, RFE)和主成分分析法(Principal Component Analysis, PCA) 5种特征选择方法进行对比,为了仅讨论特征选择对分类准确性的影响,本文方法与现有方法均采用相同的XGboost分类器。VPFNRS单粒度模型使用寻优算法找到最优粒度空间对应的最优扰动特征集进行实验,各特征选择方法性能对比如表2所示。
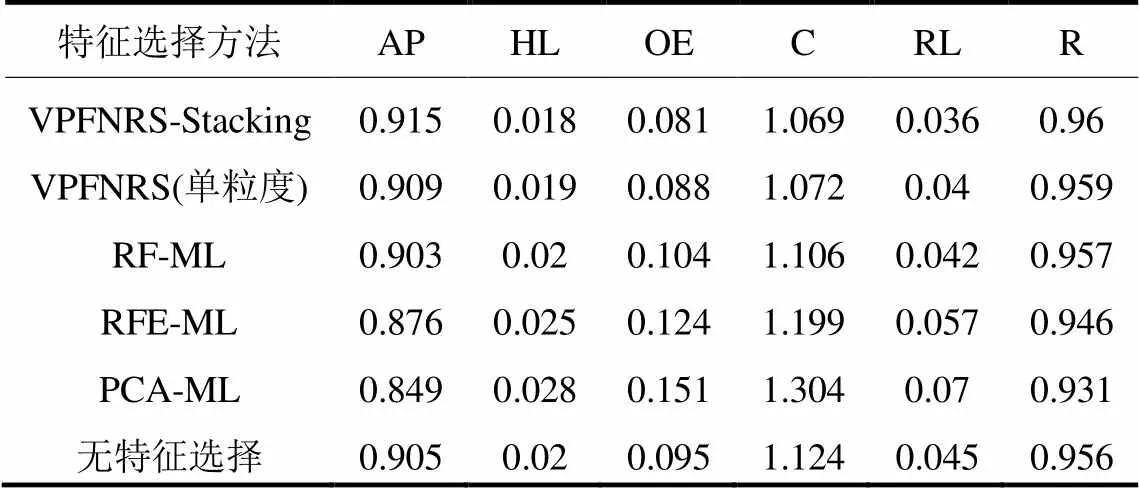
表2 各特征选择方法的性能对比
由表2可知,多粒度VPFNRS-Stacking模型相较于单粒度VPFNRS模型得到的特征具有更好的分类性能。此外,VPFNRS方法无论是单一粒度模型还是多粒度模型的特征选择和分类效果也明显优于传统的RF、RFE和PCA特征选择方法,且具有一定的抗噪能力,并有效地改善了模型的分类性能。
4.3 复合电能质量扰动分类实验
基于VPFNRS-Stacking分类方法的复合PQD扰动分类在噪声30 dB、40 dB和50 dB情况下的测试结果如表3所示。
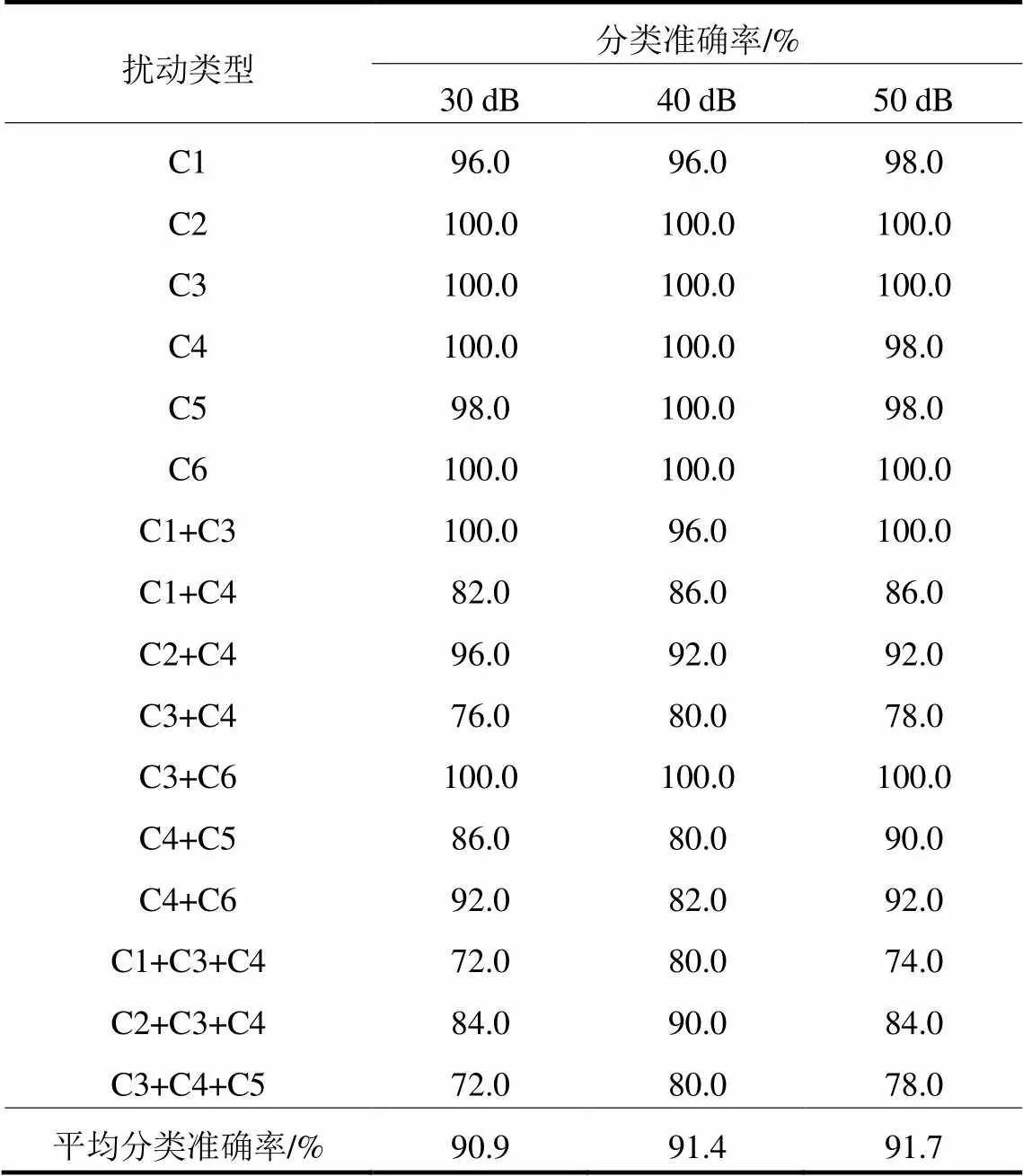
表3 16种单一和复合扰动分类准确率
为进一步对比本文方法与常用分类方法的性能,采用深度卷积神经网络[3](Deep Convolutional Neural Networks, DCNN)模型、两类分类支持向量机模型[1]和基于XGboost 的排位分类模型进行对比。其中DCNN和Binary-SVM由于不涉及排位函数,因此只使用平均分类准确率、汉明损失和召回率作为评价指标。各分类模型的性能对比如表4所示。

表4 各分类模型的性能对比
由表4可知,VPFNRS-Stacking模型的分类效果均优于其他3种分类模型。在训练样本量较小的情况下,DCNN的效果不佳。

表5 电网实测数据分析
4.4 集成分类模型对分类准确率的影响
为对比本文采用的多粒度Stacking集成分类模型与Bagging和Boosting集成分类模型的性能,在VPFNRS各粒度空间所构建的同质弱分类器的基础上应用不同的集成分类策略进行实验,实验结果如表6所示。由表6可见,基于Stacking的集成分类策略相较于其他集成分类策略具有更好的模型融合效果。
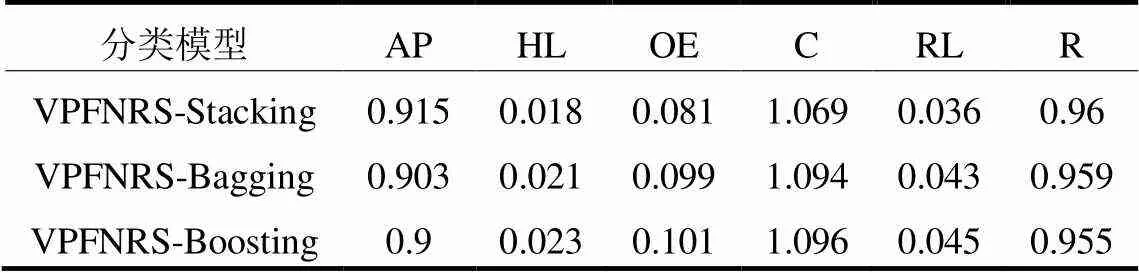
表6 各集成模型的性能对比
5 结论
本文提出一种基于多粒度特征选择和模型融合的复合电能质量扰动分类特征优化方法,并论证了该方法能够有效改善分类模型的分类性能,对复合PQD分类具有较好的准确性和有效性,结论如下:
1) 提出基于变精度模糊粗糙集模型的特征选择方法,解决了多标签数据集不同样本间特征分布的差异性以及类域的交叉重叠等造成数据模糊而难以寻找最优特征区分面的问题,提升了特征选择的效果。
2) 考虑到各粒度空间下不同扰动特征集对分类性能的影响,为防止忽略各粒度空间中对分类有益的有效信息,基于Stacking集成分类原理,提出了三层复合电能质量扰动分类器架构,构建了多粒度集成分类模型,该模型融合了各个粒度空间下的基分类器的识别能力,具有一定的自适应性。
本文在分析多标签数据时假设样本标签的重要度是一致的,而目前尚缺乏针对标签重要度不等的多标签数据特征选择模型的相关研究;此外,初始特征集合的选择仍依赖于专家经验。因此,下一步将分别从标签分布增强和初始特征选择的角度研究进一步的改进方法。
[1] 黄建明, 瞿合祚, 李晓明. 基于短时傅里叶变换及其谱峭度的电能质量混合扰动分类[J]. 电网技术, 2016, 40(10): 3184-3191.
HUANG Jianming, QU Hezuo, LI Xiaoming. Classification for hybrid power quality disturbance based on STFT and its spectral kurtosis[J]. Power System Technology, 2016, 40(10): 3184-3191.
[2] 肖湘宁. 电能质量分析与控制[M]. 北京: 中国电力出版社, 2010.
[3] 徐达, 洪文慧, 季天瑶, 等. 基于S变换和长短期记忆网络的电能质量复合扰动识别[J]. 广东电力, 2021, 34(7): 33-39.
XU Da, HONG Wenhui, JI Tianyao, et al. Composite disturbance identification of power quality based on S transform and long short term memory network[J]. Guangdong Electric Power, 2021, 34(7): 33-39.
[4] WANG S, CHEN H. A novel deep learning method for the classification of power quality disturbances classification using deep convolutional neural networks[J]. Applied Energy, 2019, 235: 1126-1140.
[5] 郑炜, 林瑞全, 王俊, 等. 基于GAF与卷积神经网络的电能质量扰动分类[J]. 电力系统保护与控制, 2021, 49(11): 97-104.
ZHENG Wei, LIN Ruiquan, WANG Jun, et al. Power quality disturbance classification based on GAF and a convolutional neural network[J]. Power System Protection and Control, 2021, 49(11): 97-104.
[6] THIRUMALA K, PAL S, JAIN T, et al. A classification method for multiple power quality disturbances using EWT based adaptive filtering and multiclass SVM[J]. Neurocomputing, 2019, 334: 265-274.
[7] 徐艳春, 高永康, 李振兴, 等. 基于VMD初始化S变换的混合动力系统电能质量扰动检测与分类[J]. 中国电机工程学报, 2019, 39(16): 4786-4798, 4980.
XU Yanchun, GAO Yongkang, LI Zhenxing, et al. Power quality disturbance detection and classification of hybrid power system based on VMD initialization S-transform[J]. Proceedings of the CSEE, 2019, 39(16): 4786-4798, 4980.
[8] TANG Qiu, QIU Wei, ZHOU Yicong. Classification of complex power quality disturbances using optimized S-Transform and Kernal SVM[J]. IEEE Transactions on Industrial Electronics, 2020, 67(11): 9715-9723.
[9] 李建文, 秦刚, 李永刚, 等. 基于布莱克曼窗S变换与数据库查询的电能质量扰动识别与分类新方法[J]. 电网技术, 2020, 44(12): 4734-4743.
LI Jianwen, QIN Gang, LI Yonggang, et al. Recognition and classification new method of power qualitydisturbances based on Blackman window S transform and database query[J]. Power System Technology, 2020, 44(12): 4734-4743.
[10] 王燕. 电能质量扰动检测的研究综述[J]. 电力系统保护与控制, 2021, 49(13): 174-186.
WANG Yan. Review of research development in power quality disturbance detection[J]. Power System Protection and Control, 2021, 49(13): 174-186.
[11] 许立武, 李开成, 罗奕, 等. 基于不完全S变换与梯度提升树的电能质量复合扰动识别[J]. 电力系统保护与控制, 2019, 47(6): 24-31.
XU Liwu, LI Kaicheng, LUO Yi, et al. Classification of complex power quality disturbances based on incomplete S-transform and Graient boosting decision tree[J]. Power System Protection and Control, 2019, 47(6): 24-31.
[12] 徐袭, 石敏. 一种基于粗糙集与小波变换的电能质量分类方法[J]. 电力自动化设备, 2005, 25(11): 15-18.
XU Xi, SHI Min. Power quality classification based on rough set and wavelet transform[J]. Electric Power Automation Equipment, 2005, 25(11): 15-18.
[13] WANG Changzhong, SHAO Mingwen, HE Qiang, et al. Feature subset selection based on fuzzy neighborhood rough sets[J]. Knowledge Based Systems, 2016, 111: 173-179.
[14] WANG Changzhong, HUANG Yang, SHAO Mingwen, et al. Fuzzy rough set-based attribute reduction using distance measures[J]. Knowledge Based Systems, 2018, 164: 205-212.
[15] CHEN Panpan, LIN Menglei, LIU Jinghua, et al. Multi-label attribute reduction based on variable precision fuzzy neighborhood rough set[J]. Digital Object Identifier, 2020, 8: 133565-133576.
[16] 段洁, 胡清华, 张灵均, 等. 基于邻域粗糙集的多标记分类特征选择算法[J]. 计算机研究与发展, 2015, 52(1): 56-65.
DUAN Jie, HU Qinghua, ZHANG Lingjun, et al. Feature selection for multi-label classification based on neighborhood rough sets[J]. Journal of Computer Research and Development, 2015, 52(1): 56-65.
[17] RIBERIO M H D M, COELHO L D S. Ensemble approach based on bagging, boosting and stacking for short term prediction in agribusiness time series[J]. Applied Soft Computing Journal, 2020, 86.
[18] 李长松, 刘凯, 肖先勇, 等. 基于条件互信息特征选择法和Adaboost算法的电能质量复合扰动分类[J]. 高电压技术, 2019, 45(2): 579-585.
LI Changsong, LIU Kai, XIAO Xianyong, et al. Classification of multiple power quality disturbances based on conditional mutual information feature selection method and Adaboost algorithm[J]. High Voltage Engineering, 2019, 45(2): 579-585.
[19] 汪颖, 陈春林, 肖先勇. 电压暂降源异质堆叠集成学习识别法[J]. 电力系统保护与控制, 2021, 49(15): 1-8.
WANG Ying, CHEN Chunlin, XIAO Xianyong. Heterogeneous stacking integrated learning identification method for voltage sag sources[J]. Power System Protection and Control, 2021, 49(15): 1-8.
[20] RADHAKRISHNAN P, RAMAIYAN K, VINAYAGAM A, et al. A Stacking ensemble classification model for detection and classification of power quality disturbances in PV integrated power network[J]. Measurement, 2021, 175.
[21] 杨剑锋, 姜爽, 石戈戈. 基于分段改进S变换的复合电能质量扰动识别[J]. 电力系统保护与控制, 2019, 47(9): 64-71.
YANG Jianfeng, JIANG Shuang, SHI Gege. Classification of composite power quality disturbances based on piecewise-modified S transform[J]. Power System Protection and Control, 2019, 47(9): 64-71.
[22] LI Jinsong, LIU Hao, WANG Dengke, et al. Classification of power quality disturbance based on s-transform and convolution neural network[J]. Frontiers in Energy Research, 2021, 9.
[23] 田振果, 傅成华, 吴浩, 等. 基于HHT的电能质量扰动定位与分类[J]. 电力系统保护与控制, 2015, 43(16): 36-42.
TIAN Zhenguo, FU Chenghua, WU Hao, et al. Power quality disturbance for location and classification based on HHT[J]. Power System Protection and Control, 2015, 43(16): 36-42.
[24] 黄南天, 王达, 刘座铭, 等. 复杂噪声环境下电能质量复合扰动特征选择[J]. 仪器仪表学报, 2018, 39(4): 82-90.
HUANG Nantian, WANG Da, LIU Zuoming, et al. Feature selection of composite power quality disturbances under complex noise environment[J]. Chinese Journal of Scientific Instrument, 2018, 39(4): 82-90.
[25] IEEE recommended practice for monitoring electric power quality: IEEE Std. 1159—2009[S]. New York: IEEE, 1995.
[26] 陈振宇, 刘金波, 李晨, 等. 基于LSTM与XGBoost组合模型的超短期电力负荷预测[J]. 电网技术, 2020, 44(2): 614-620.
CHEN Zhenyu, LIU Jinbo, LI Chen, et al. Ultra short-term power load forecasting based on combined LSTM-XGBoost model[J]. Power System Technology, 2020, 44(2): 614-620.
Multiple power quality disturbance classification feature optimization based on multi-granularity feature selection and model fusion
RUAN Zihang, XIAO Xianyong, HU Wenxi, ZHENG Zixuan, WANG Ying
(College of Electrical Engineering, Sichuan University, Chengdu 610065, China)
Modern power systems with “double high” characteristics make power quality disturbance patterns more complex, and the accurate classification of multiple power quality disturbances becomes more difficult. In the feature extraction stage of traditional power quality disturbance classification methods, the extracted features are determined artificially. Thus, it is difficult to judge whether the extracted features are adequate for classification problems, and the coupling of multiple feature distribution will affect the separability of disturbance features. Therefore, this paper proposes a feature selection method based on granular computing to optimize the performance of the classification. Based on the original feature set, a multi-granularity space is constructed to reflect the difference in feature distribution. Then the optimal feature subsets under each granularity are mined to determine the effective and redundant classification features. The homogeneous base classifiers trained by optimal feature subsets corresponding to different granularity spaces are fused by the ensemble model. A new multi-granularity ensemble classification model for power quality disturbance is proposed. This method overcomes the problem of the existing techniques by searching for the optimal valuable information of a single granularity space in a multi-granularity classification, leading to other granularity spaces losing the useful information. The simulation results show that the multi-granularity feature selection algorithm can extract useful features for classification, and an integrated model can improve the classification performance of the model.
power quality; multiple disturbance; feature selection; multi-granularity space; integrated classification
10.19783/j.cnki.pspc.211199
国家自然科学基金项目资助(51807126);中央高校基本科研业务费专项资金资助
This work is supported by the National Natural Science Foundation of China (No. 51807126).
2021-08-31;
2021-11-11
阮梓航(1997—),男,硕士研究生,研究方向为电能质量与优质供电;E-mail: 1069612544@qq.com
肖先勇(1968—),男,博士,教授,研究方向为电能质量与优质供电;E-mail: xiaoxianyong@163.com
胡文曦(1993—),男,通信作者,博士,讲师,研究方向为电力扰动数据分析与应用。E-mail: 408803186 @qq.com
(编辑 魏小丽)

