基于递归通用信号延迟叠加算子的单相锁相环
刘 勇,杨 涛,盘宏斌,曾 力,曹 雷
基于递归通用信号延迟叠加算子的单相锁相环
刘 勇1,杨 涛1,盘宏斌1,曾 力1,曹 雷2
(1.湘潭大学自动化与电子信息学院,湖南 湘潭 411105;2.贵州电网有限责任公司都匀供电局,贵州 都匀 558000)
当电网电压存在谐波与直流偏移时,传统锁相环无法精确锁相。为此,提出一种基于递归通用信号延迟叠加算子的改进单相锁相环算法。该方法在锁相环前级引入递归通用信号延迟叠加算子,以产生正交信号并滤除谐波。接着在两相静止坐标系下,构建延迟采样周期滤波器,通过将正交分量延迟两个采样周期的方法抑制直流偏移。所提单相锁相环技术能够消除直流偏移和谐波干扰的影响,快速准确地获取基波和所需的特定次谐波信息,同时具有良好的动态性能和稳定性。最后,仿真与实验结果证明了该方法的可行性。
单相锁相环;延迟信号叠加;直流偏移;谐波分离;同步信号检测
0 引言
在有源电力滤波器和分布式发电系统等能源和电力应用中,快速准确地获取电网电压的相位、频率和谐波成分等信息是十分重要的[1-4]。锁相环结构(Phase-Locked Loop, PLL)由鉴相器、环路滤波器和压控振荡器组成,结构简单、易于实现,被广泛应用于电网同步[5-9]。
不同于三相供电系统,在单相系统中,由于只有一个输入信号,锁相环结构更为复杂[10]。近年来,基于正交信号发生器(Quadrature Signal Generator, QSG)的锁相环因其在非理想电网电压条件下的鲁棒性,在单相系统中发挥着至关重要的作用[11-14]。
文献[15]详细研究了包括二阶广义积分器(Second-Order Generalized Integrator, SOGI)以及复系数滤波器(Complex-Coefficient Filter, CCF)在内的多种正交信号发生技术。这些方法通过单相电网电压信号生成虚拟正交信号,具有动态响应慢、对谐波敏感等缺点。文献[16]推导了一种通用信号延迟叠加算子(Generalized Delayed Signal Superposition Operator, GDSS),GDSS算子能够实现对单相输入信号中任意所选频率信号的提取,并生成其对应的正交信号。基于这种GDSS算子,文献[17]提出了一种基于GDSS算子的锁相环结构(GDSS-PLL),可以在谐波干扰下快速准确地提取基波及谐波信号同步信号。
在实际电网中,由于电网故障、数字信号处理器中的 A/D 转换、地磁现象、半波整流、电流互感器饱和以及分布式发电系统的直流注入等原因[18-19],PLL输入电压中会产生直流偏移。而直流偏移会导致PLL输出波形中含二倍频波动[20]。文献[21]给出了直流偏移对锁相环性能影响的定量分析。结果表明,随着前级输入中直流偏移量的增大,锁相环的带宽必须相应减小。

针对以上问题,本文在GDSS-PLL的基础上,提出一种改进单相锁相环技术。首先,在离散域下基于直接形式的GDSS算子推导GDSS算子的递归实现形式。相对直接形式GDSS算子而言,递归GDSS算子减小了实现复杂度,且降低了计算量。然后,提出了一种延迟采样周期滤波器(Delay Sampling Period Filter, DSPF)以滤除PLL输入中的直流偏移。并对所提DSPF算法的抗噪性能进行研究,给出了相应的解决方案。接着,通过递归GDSS算子提取单相输入信号中的基波及所需谐波信号,并生成其对应的正交信号。同时引入DSPF滤除所得信号中的直流偏移。最后通过基于同步旋转坐标系的锁相环(Synchronous Reference Frame-Phase Locked Loop, SRF-PLL)获取电网基波频率和相位信息。仿真与实验结果表明,所提锁相方法在不同电网故障下都能保持良好的同步性能。
1 通用信号延迟叠加算子
1.1 滤波原理介绍及推导

文献[16]提出一种GDSS算子,其表达式为
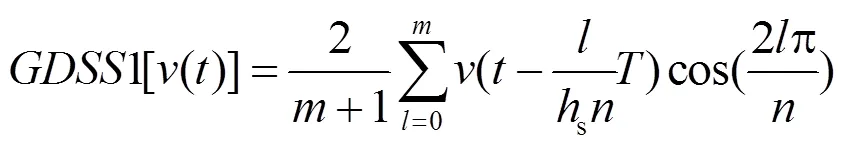

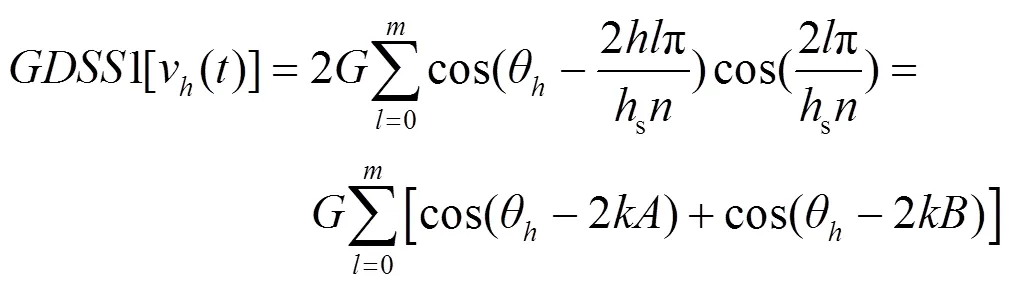
根据文献[26]给出的三角函数叠加公式,可以将式(4)进一步简化为
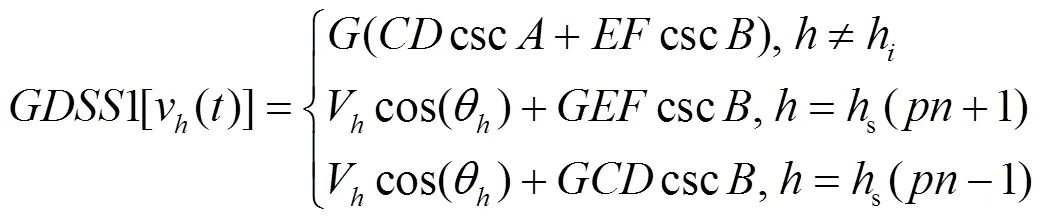

图1 GDSS直接实现形式
Fig. 1 Direct-form of GDSS
1.2 递归实现形式


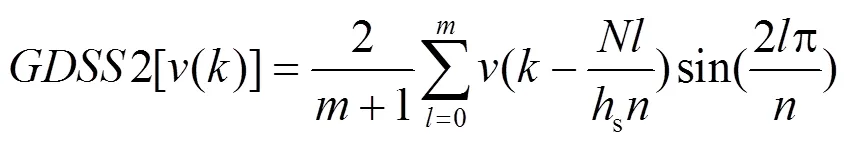

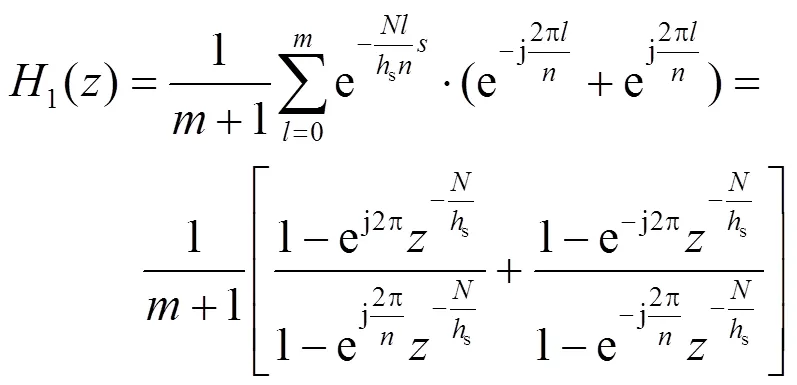
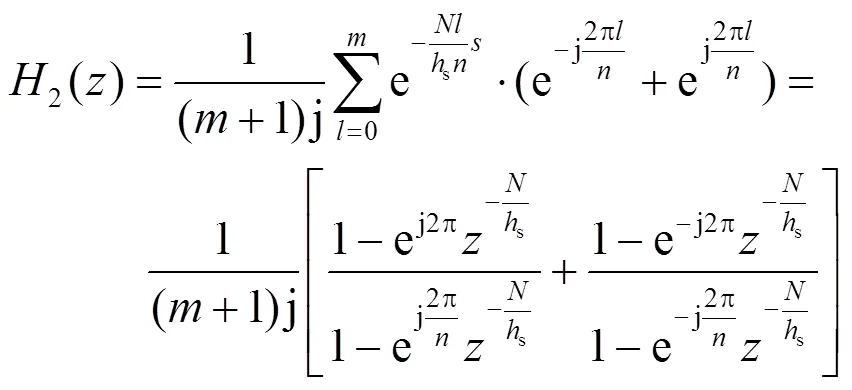

其中,j为虚部,根据式(11),式(9)和式(10)可以进一步简化为

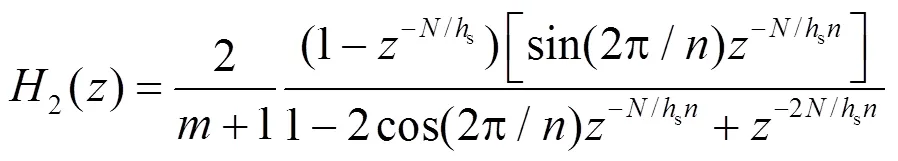

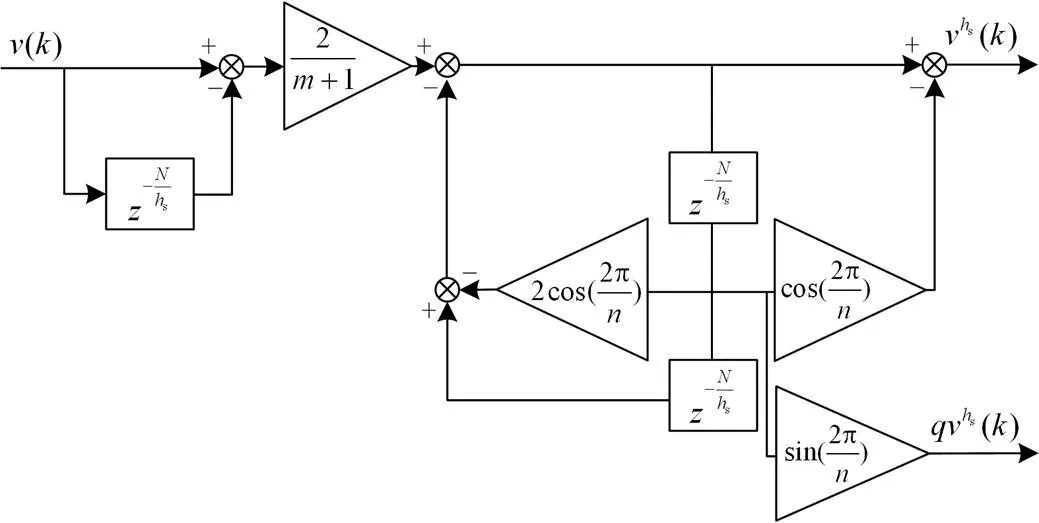
图2 GDSS递归实现形式

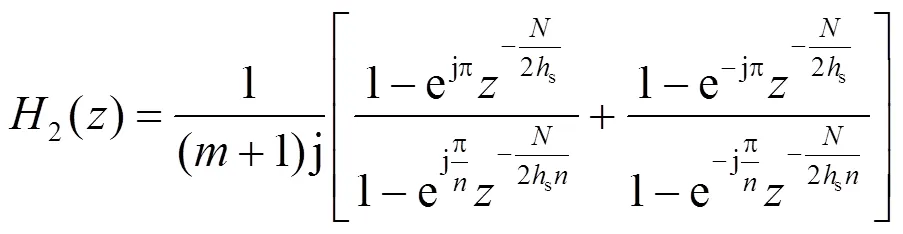
进一步推导,式(14)和式(15)可表示为
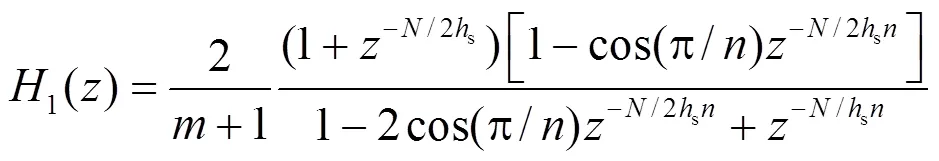
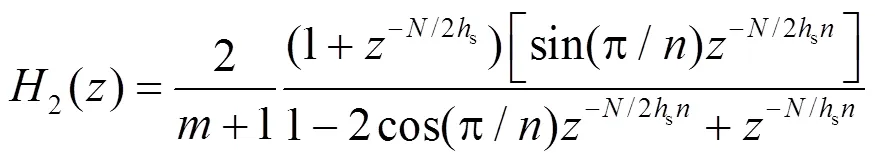
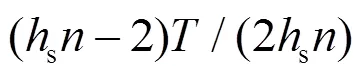

表1 RGDSS参数表
2 直流偏移滤除方法

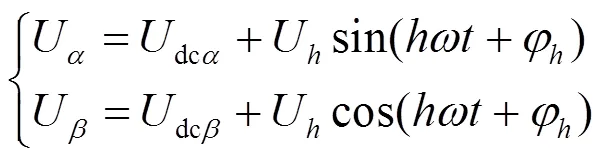
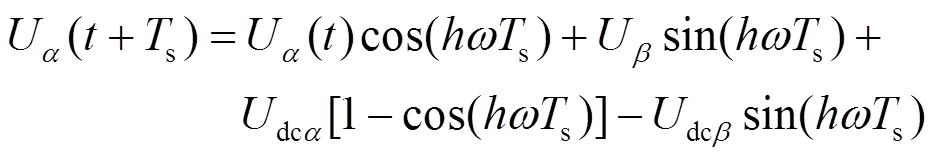

根据式(19)和式(20),通过推导可得次谐波在轴上的分量,可表示为
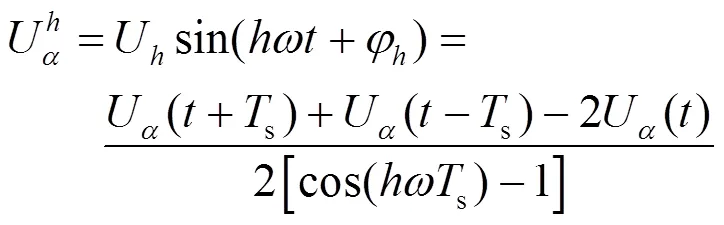
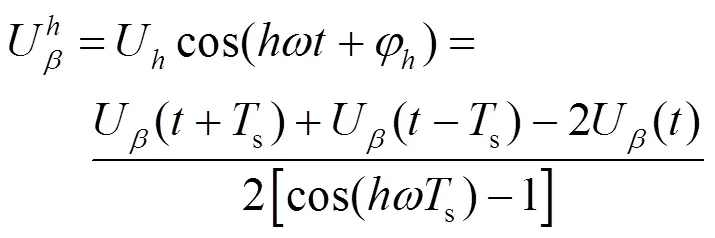
在工程实际中,DSPF算法需要在离散域内实现,对式(21)和式(22)进行离散化。


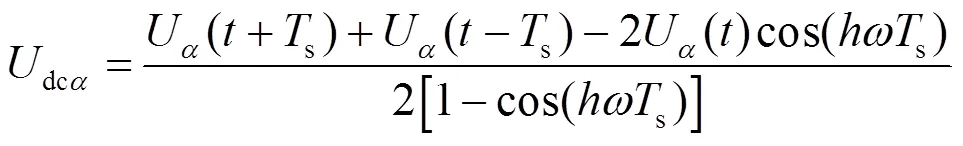

所提DSPF算法可以滤除直流偏移,理论动态响应时间仅为两个采样周期。与目前广泛应用的DSC算法相比,动态响应时间明显缩短。

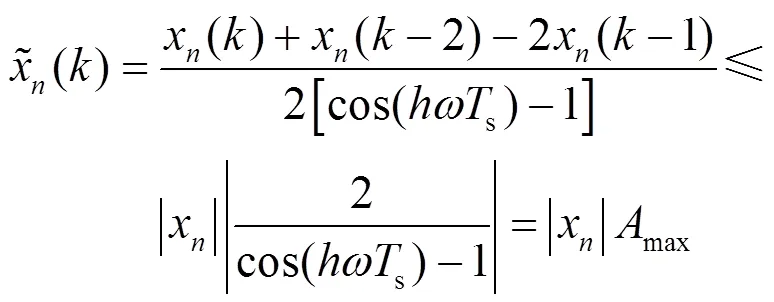

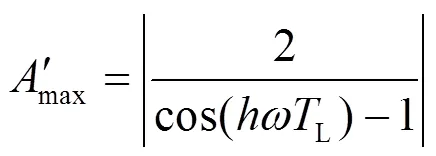


从图4可以看出,基波频率和相位同步是通过SRF-PLL实现的,但其性能主要由GDSS算子和DSPF模块所组成的前置滤波级决定。因此可以根据具体应用和控制要求灵活设计GDSS算子和DSPF模块的参数和个数。由于预滤波级的RGDSS和DSPF模块滤除了谐波和直流偏移,输入信号没有失真,因此SRF-PLL的带宽可以设置的足够宽,PI参数可以按照文献[29]所述设计。
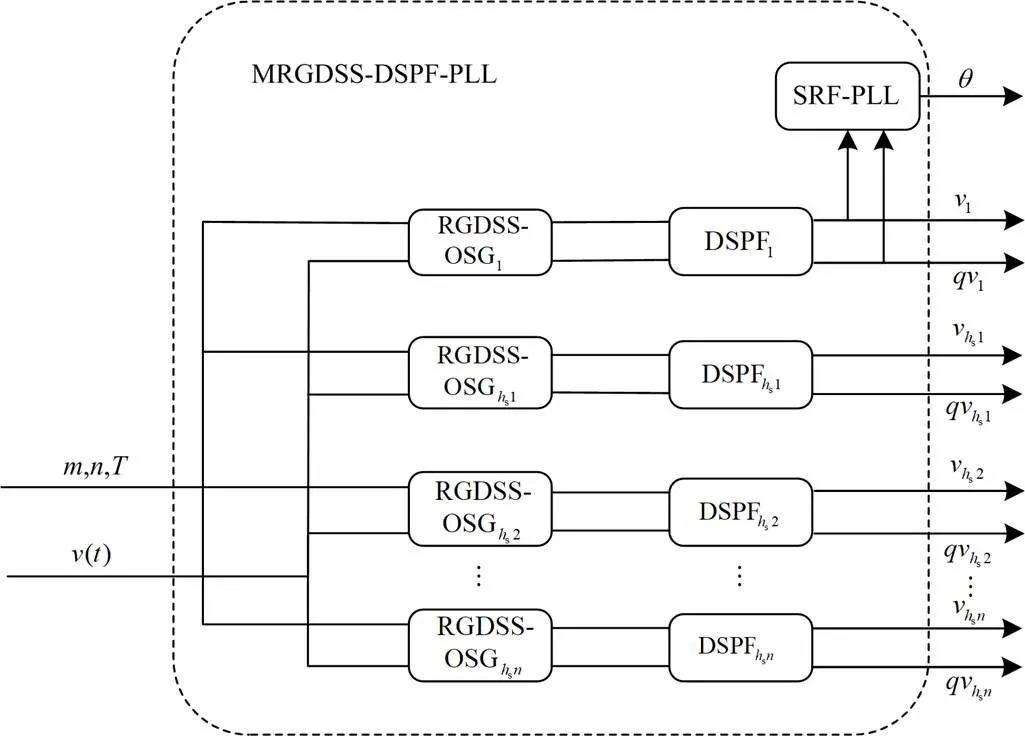
图4 MRGDSS-DSPF-PLL结构图
3 仿真结果分析
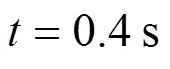
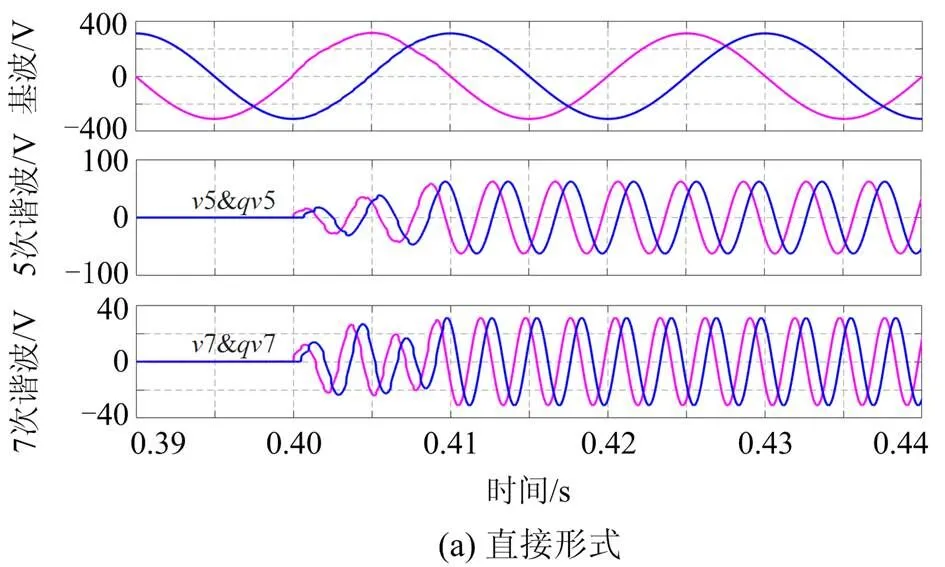
为进一步检验MRGDSS-DSPF-PLL的动态性能和稳定性,设置了电压跌落、相角跳变和频率跳变3种工况。
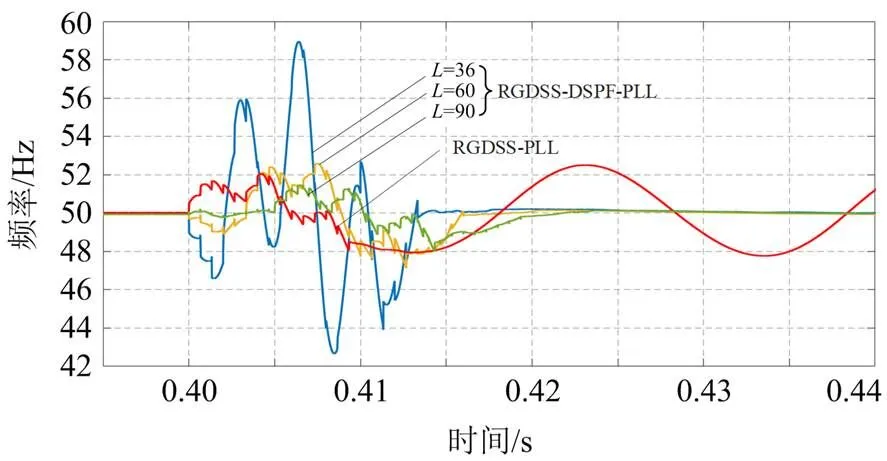
图6 在直流偏移和谐波干扰下的仿真结果
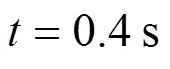
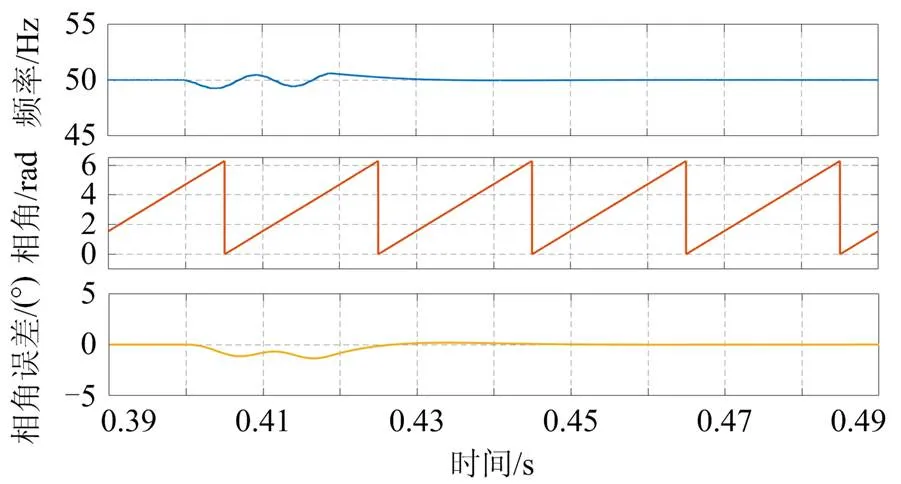
图7 电压跌落的仿真结果
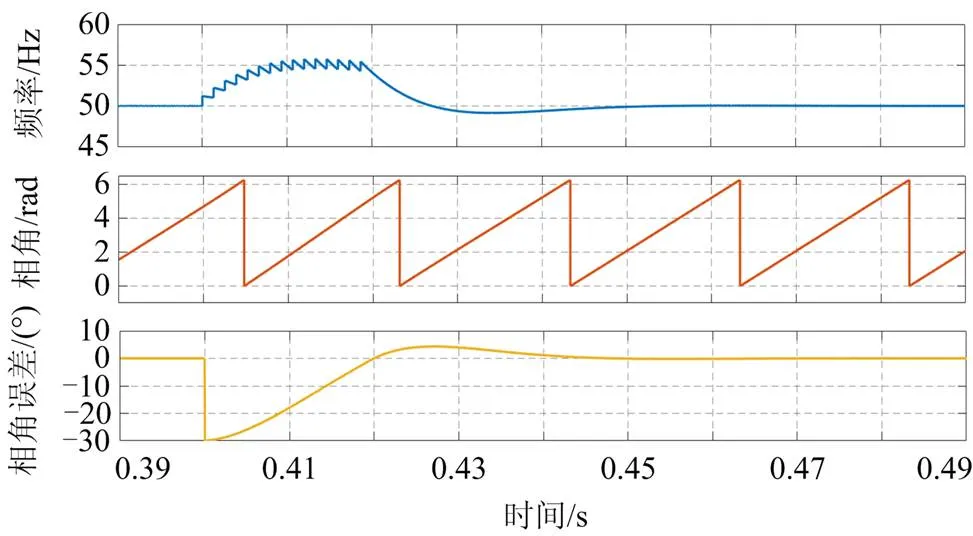
图8 相角跳变的仿真结果

图9 频率跳变的仿真结果
4 实验结果分析
本文实验基于StarSim半实物平台进行验证,如图10所示,实验平台主要由快速控制原型器、I/O信号转接板、实时仿真器以及主机操控平台组成。通过基于FPGA的实时仿真器模拟单相电压信号,锁相环算法经过编译后下载到快速控制原型器中运行,锁相结果可通过示波器或上位机显示。实验中参数设置与仿真一致,实验结果如图11所示。

图10 半实物平台组成
所提单相锁相环在直流偏移和谐波干扰下的实验结果如图11(a)所示。对比图6仿真结果以及图11的实验结果,动态过程超调量和响应时间基本一致,可以看出所提方法能够实现基波频率快速准确的估计,由RGDSS和直流偏移滤除算法所组成的前置滤波级可以有效且快速地消除直流偏移和谐波干扰的影响,进而使SRF-PLL成功锁相。
图11(b)是电压跌落时锁相环的输出波形,可以看到锁相环动态响应时间较短,约25 ms时锁相环输出达到稳定,且频率波形超调也较小,约为4%,与仿真结果相吻合。图11(c)是相角跳变时的实验结果,由于加入了DSPF算法,频率估计过程超调量较大。频率突变时的实验结果如图11(d)所示,在频率偏移情况下锁相环仍能准确估计频率。实验证明了所提单相锁相环结构在电网常见故障下仍能精准锁相,尽管DSPF算法会增大频率估计时动态响应的超调量,但能通过调节使其表现出满意的性能。


图11 实验结果
5 结论

[1] PRAKASH S, SINGH J K, BEHERA R K, et al. A type-3 modified SOGI-PLL with grid disturbance rejection capability for single-phase grid-tied converters[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 4242-4252.
[2] MENG Xin, ZHU Yanbin, LIU Lei, et al. Research on power control strategy of household-level electric power router based on hybrid energy storage droop control[J]. Protection and Control Modern Power Systems, 2021, 6(2): 178-180.
[3] BAMIGBADE A, KHADKIKAR V, AL HOSANI M. Single-phase type-1 frequency-fixed FLL for distorted voltage condition[J]. IEEE Transactions on Industrial Electronics, 2021, 68(5): 3865-3875.
[4] TANG M, BIFARETTI S, PIPOLO S, et al. A novel low computational burden dual-observer phase-locked loop with strong disturbance rejection capability for more electric aircraft[J]. IEEE Transactions on Industry Applications, 2021, 57(4): 3832-3841.
[5] 王佳浩, 潘欢, 纳春宁, 等. 复杂电网环境下基于DDM-QT1-PLL的并网同步方法[J]. 电力系统保护与控制, 2020, 48(13): 132-141.
WANG Jiahao, PAN Huan, NA Chunning, et al. Grid-connected synchronization method based on DDM-QT1-PLL under complex grid conditions[J]. Power System Protection and Control, 2020, 48(13): 132-141.
[6] 朱建红, 黄琼, 孟棒棒. 基于分量滤波直接解耦风电并网锁相环设计[J]. 电力系统保护与控制, 2018, 46(24): 135-141.
ZHU Jianhong, HUANG Qiong, MENG Bangbang. Direct decoupling wind power grid-connected phase-locked loop design based oncomponent filtering[J]. Power System Protection and Control, 2018, 46(24): 135-141.
[7] 汪娟娟, 龚英明, 文兆新, 等. 一种基于级联延迟信号消去锁相环的高压直流输电同步触发控制[J]. 中国电机工程学报, 2021, 41(2): 524-536.
WANG Juanjuan, GONG Yingming, WEN Zhaoxin, et al. A firing control of HVDC based on cascaded delayed signal cancellation phase locked loop[J]. Proceedings of the CSEE, 2021, 41(2): 524-536.
[8] 许津铭, 卞申一阳, 钱浩, 等. 弱电网下单相并网逆变器延时锁相环的鲁棒控制及优化方法[J]. 中国电机工程学报, 2020, 40(7): 2062-2070, 2386.
XU Jinming, BIAN Shenyiyang, QIAN Hao, et al. Robust control and optimization of delay-based phase-locked loop of single-phase grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2020, 40(7): 2062-2070, 2386.
[9] 朱建红, 顾菊平, 孟棒棒, 等. 软硬锁相环在分布式风电并网控制中的联合应用[J]. 太阳能学报, 2022, 43(1): 36-43.
ZHU Jianhong, GU Juping, MENG Bangbang, et al. Integrated application of software and hardware phase-locked loop on grid connection control for distributed wind power[J]. Acta Energiae Solaris Sinica, 2022, 43(1): 36-43.
[10] 张振波, 王海云, 王维庆, 等. 基于改进型环路滤波器的单相锁相环[J]. 电力系统保护与控制, 2021, 49(13): 135-141.
ZHANG Zhenbo, WANG Haiyun, WANG Weiqing, et al. Single phase locked loop based on improved loop filter[J]. Power System Protection and Control, 2021, 49(13): 135-141.
[11] SALEEM K, ALI Z, MEHRAN K. A single-phase synchronization technique for grid-connected energy storage system under faulty grid conditions[J]. IEEE Transactions on Power Electronics, 2021, 36(10): 12019-12032.
[12] 陈四雄, 易龙强, 黄文俊, 等. 基于构造非正交向量的单相锁相技术研究[J]. 电工技术学报, 2019, 34(2): 398-408.
CHEN Sixiong, YI Longqiang, HUANG Wenjun, et al. Single-phase phase-locked technique based on constructing non-orthogonal vector[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 398-408.
[13] GOLESTAN S, GUERRER J M, VASQUEZ J C. A nonadaptive window-based PLL for single-phase applications[J]. IEEE Transactions on Power Electronics, 2018, 33(1): 24-31.
[14] SALEEM K, MEHRAN K, ALI Z. An improved pre-filtering moving average filter based synchronization algorithm for single-phase V2G application[C] // 2020 IEEE Energy Conversion Congress and Exposition (ECCE), October 11-15, 2020, Detroit, MI, USA: 4088-4093.
[15] HAN Y, LUO M, ZHAO X, et al. Comparative performance evaluation of orthogonal-signal-generators- based single -phase PLL algorithms—a survey[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3932-3944.
[16] 卢勇, 肖国春, 臧龙飞. 一种基于通用信号延迟叠加算子的单相电网基波及谐波同步算法[J]. 中国电机工程学报, 2017, 37(7): 1974-1982.
LU Yong, XIAO Guochun, ZANG Longfei. Single-phase grid fundamental and harmonic component detection method based on generalized delayed signal superposition[J]. Proceedings of the CSEE, 2017, 37(7): 1974-1982.
[17] LU Y, XIAO G, WANG X, et al. Grid synchronization with selective harmonic detection based on generalized delayed signal superposition[J]. IEEE Transactions on Power Electronics, 2018, 33(5): 3938-3949.
[18] KANJIYA P, KHADKIKAR V, ELMOURSI M S. Adaptive low-pass filter based DC offset removal technique for three-phase PLLs[J]. IEEE Transactions on Industrial Electronics, 2018, 65(11): 9025-9029.
[19] 李欣悦, 李凤婷, 尹纯亚, 等. 直流双极闭锁故障下送端系统暂态过电压计算方法[J]. 电力系统保护与控制, 2021, 49(1): 1-8.
LI Xinyue, LI Fengting, YIN Chunya, et al. Transient overvoltage calculation method of HVDC sending-end system under DC bipolar blocking[J]. Power System Protection and Control, 2021, 49(1): 1-8.
[20] MOHAMADIAN S, PAIRO H, GHASEMIAN A. A straightforward quadrature signal generator for single-phase SOGI-PLL with low susceptibility to grid harmonics[J]. IEEE Transactions on Industrial Electronics, 2022, 69(7): 6997-7007.
[21] LUO S, WU F. Improved two-phase stationary frame EPLL to eliminate the effect of input harmonics, unbalance, and DC offsets[J]. IEEE Transactions on Industrial Informatics, 2017, 13(6): 2855-2863.
[22] 张建武, 陈权, 李国丽, 等. 非理想电网下改进二阶广义积分器锁相环研究[J]. 电力电子技术, 2021, 55(7): 7-11.
ZHANG Jianwu, CHEN Quan, LI Guoli, et al. Research on improved second order generalized integerator phase-locked loop in non-ideal power grid[J]. Power Electronic, 2021, 55(7): 7-11.
[23] GOLESTAN S, GUERRERO J M, VASQUEZ J C. DC-offset rejection in phase-locked loops: a novel approach[J]. IEEE Transactions on Industrial Electronics, 2016, 63(8): 4942-4946.
[24] 回楠木, 王大志, 李云路. 改进型DSC的并网锁相环直流偏移消除方法[J]. 东北大学学报(自然科学版), 2018, 39(11): 1526-1531.
HUI Nanmu, WANG Dazhi, LI Yunlu. DC-offset elimination method for grid-connected phase-locked loop by modified DSC[J]. Journal of Northeastern University (Natural Science Edition), 2018, 39(11): 1526-1531.
[25] 曾君, 岑德海, 陈润, 等. 针对直流偏移和谐波干扰的单相锁相环[J]. 电工技术学报, 2021, 36(16): 3504-3515.
ZENG Jun, CEN Dehai, CHEN Run, et al. Single-phase phase-locked loop for DC offset and harmonic interference[J]. Power System Protection and Control, 2021, 36(16): 3504-3515.
[26] GRADSHTEYN I S, RYZHIK I M. Table of integrals, series, and products[M]. San Diego: Academy Press, 2007, 36.
[27] 杨旭红, 吴斌, 孙克帅, 等. 一种频率自适应延迟周期法的锁相环研究[J]. 电机与控制学报, 2020, 24(2): 96-101.
YANG Xuhong, WU Bin, SUN Keshuai, et al. Frequency adaptive phase-locked loop based on delayed signal cancellation[J]. Electric Machines and Control, 2020, 24(2): 96-101.
[28] SUMATHI P, JANAKIRAMAN P A. Integrated phase-locking scheme for SDFT-based harmonic analysis of periodic signals[J]. IEEE Transactions on Circuits Systems II: Express Briefs, 2008, 55(1): 51-55.
[29] WANG Y F, LI Y W. Three-phase cascaded delayed signal cancellation PLL for fast selective harmonic detection[J]. IEEE Transactions on Industrial Electronics, 2013, 60(4): 1452-1463.
Single-phase phase-locked loop based on recursive implementation of generalized delayed signal superposition
LIU Yong1, YANG Tao1, PAN Hongbin1, ZENG Li1, CAO Lei2
(1. School of Automation and Electronic Information, Xiangtan University, Xiangtan 411105, China;2. Duyun Power Supply Bureau, Guizhou Power Grid Co., Ltd., Duyun 558000, China)
When there are harmonics and DC offset in a grid voltage, the traditional phase-locked loop (PLL) cannot accurately realize phase lock. Hence, an improved single-phase phase-locked loop algorithm based on recursive-form generalized delayed signal superposition (RGDSS) operators is proposed. To produce the orthogonal signals and filtering of the harmonic, RGDSS operators are introduced into the pre-stage of the PLL. Then in a two-phase stationary reference frame, a delayed sampling period filter is constructed to suppress the DC offset by delaying the orthogonal component by two sampling periods. The proposed PLL, which has good dynamic performance and stability, can effectively eliminate the influence of DC offset and harmonics, and obtain the fundamental and desired harmonic information quickly and accurately. Finally, the feasibility of the method is verified by simulation and experiment.
single-phase phase-locked loop; delayed signal superposition; DC offset; harmonic separation; detection of synchronizing signal
10.19783/j.cnki.pspc. 211175
国家自然科学基金项目资助(51577162);湖南省自然科学基金项目资助(2021JJ30674)
This work is supported by the National Natural Science Foundation of China (No. 51577162).
2021-08-27;
2021-12-28
刘 勇(1976—),男,硕士,副教授,研究方向为微网稳定性和新能源微网逆变器;E-mail: xtdx_ly@163.com
杨 涛(1995—),男,通信作者,硕士研究生,研究方向为新能源并网锁相环技术;E-mail: 2945185118@qq.com
盘宏斌(1972—),男,博士,教授,研究方向为可再生能源发电与并网技术。E-mail: pan_hongbin@xtu.edu.cn
(编辑 许 威)

