基于合理遗忘历史样本的房地产价格非线性预测

周子英

(湖南工程学院 管理学院，湖南 湘潭 411104)

0 引言

房地产价格受到房地产供给、需求以及预期等多种因素的影响，其价格的走势存在一定的规律性[1]。近年来，由于中国的经济、城镇化速度大力推进，导致房地产价格处于不断上涨的态势。由于房地产作为一种商品，必然受到供求关系的影响，此外，房地产作为一种生活的必须品，再加上其又具有保值增值的特性，具有一定的投资性，对消费者的心理预期影响较大，因此，房地产价格预测受到了越来越多人的关注[2]。

针对房地产价格预测问题，国内外专家进行了大量研究，提出许多房地产价格预测方法。传统房地产价格预测基于多元回归预测法进行建模，该方法简单、易实现，但难以准确描述房地产价格的时变性、非平稳性，预测结果不理想[2,3]。房地产价格受到多种因素影响，具有混沌性和周期性，为此，一些学者提出了基于神经网络、贝叶斯网络、隐马尔科夫链、支持向量机等非线性的房地产价格预测模型，获得比较理想的预测结果[4-7]。其中极限学习机(extreme learning machine，ELM)是一种新型的前馈神经网络，根据Moore-Penrose广义逆矩阵理论，将训练迭代转化为线性方程组求解，一次可完成网络训练，而传统神经网络需要多次迭代过程确定网络输出权值，因此，ELM大幅度提高了网络预测建模效率[8]。房地产价格历史数据是一种典型的时间序列数据，数据间具有明显的时序关联性，同时，由于房地产价格数据具有非线性、时变性，随着新的输入、输出数据不断得到新的数据，房地产价格在不断地变化，为了使模型能准确地反映出房地产价格，就要用新的数据描述模型，而与当前状态相关性较小的旧数据可以忽略或所占的比重应降低；同时根据“近大远小”的原理(距离预测部分近的信息对未来预测结果影响更大)，为此，需要对训练样本进行合理选择，选择与预测点关联比较强的历史样本进行房地产价格建模与预测。为此，有学者提出利用在线贯序极限学习机(OS-ELM)进行时间预测预测，在预测时，首先在初始训练阶段计算出ELM神经网络的初始网络权值，然后随首新的训练样本的加入，网络权值亦可以在初始网络权值的基础上进行递推[9,10]。由于OS-ELM模型假设新、旧训练样本对时间序列数据的预测结果具有同等程度的重要性，采用等权处理，难以准确反映不同训练样本对预测结果的不同影响；再者，OS-ELM模型只要获得新训练样本，就会机械的更新网络输出权值，缺乏灵活性，增加了不必要的计算量[11]。

为了提高房地产价格的预测精度，针对房地产价格时间序列的特殊性，提出了一种基于合理遗忘历史样本的房地产价格预测模型(ELM，RF-ELM)，并通过房地产价格仿真实验对模型的预测性能加以验证。

1 在线贯序极限学习机(OS-ELM)

前馈神经网络采用梯度下降算法调整网络权重，存在学习速度慢、易陷入局部最小值、出现过度训练等缺陷，针对这些问题，Huang等根据摩尔-彭罗斯(MP)广义逆矩阵理论提出了极限学习机(ELM)算法，该算法可以通过一步计算就可以解析出网络的权值，极大的是高了网络的计算速度和泛化能力。设收集的训练集为：表示重构后的间序列，τ为延迟时间，m为相空间重构的嵌入维数，那么基于ELM的预测模型为：

式中，αi为连接第i个神经元的输入权值；bi为第i个神经元的偏差；k表示训练集的样本数；βi为第i个神经元的输出权值。

采用矩阵形式将式(1)变为：

式中，Tk为输出向量；βk为输出权值；Hk为神经元矩阵，表示如下：

对式(2)进行求解得到如下输出权值：

通过以上输出权值，可得训练后的ELM预测模型为：

式中，t和x分别为模型的输入和输出。

ELM是一种离线学习算法，难以对训练样本进行合理选择学习，为此，学者提出了在线贯序极限学习机(OS-ELM)，算法具体步骤如下：

（1）：在满足K≥L的条件下，根据时间序列Sk计算预测模型的初始输出权值：

（2）：设获得新的训练样本(xk+1,tk+1)，那么可以将它组合到训练集中，然后根据式(6)计算输出权值Pk+1与βk+1：

式 中 ，hk+1=[f(α1xk+1+b1)f(α2xk+1+b2) …f(αLxk+1+bl)]

（3）：训练集的样本数加1，并跳转到step2。

（4）：不断重复上述步骤，直到所有训练集样本均参加训练为止。

2 RF-ELM的房地产价格预测模型

2.1 RF-ELM模型

为解决OS-ELM在房地产价格预测时存在的不足，提出一种基于合理遗忘选择历史样本的房地产价格模型(RF-ELM)。假设当前训练集包含k个房地产价格样本：(x1,t1)，(x2,t2)，…，(xk,tk)，根据式(4)计算输出权值βk，如果有新的房地产价格训练样本(xk+1,tk+1)加入到训练集时，那么输出权值βk+1计算公式为：

式中，输出权值βk+1的都由旧的房地产价格训练集构成，需要对它们进行加权，这样式(8)变成为：

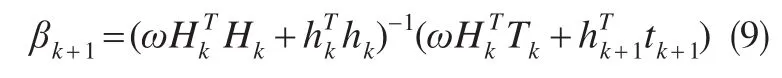
式中，ω为遗忘因子。

通过引入ω，减弱旧训练样本对预测结果影响，当ω值过小时，那么相对应的旧训练样本就被丢弃，新训练样本对预测结果影响间接增强。令

对(9)式两端同时求逆可得：

将式(11)代入式(9)，输出权值βk的递推更新方式为：

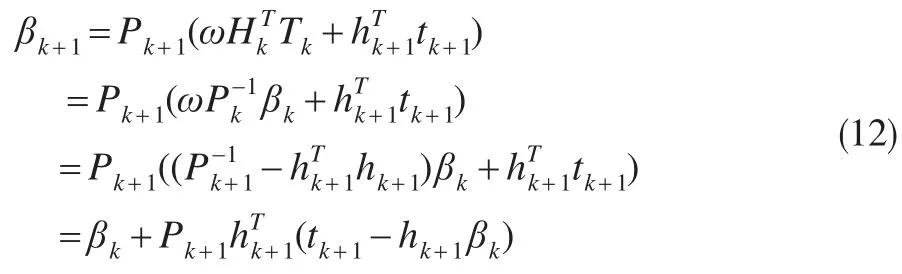
在式(9)引入Sherman-Morrison矩阵进行求逆，Pk的递推更新方式为：

2.2 RF-ELM的房地产价格预测步骤

(1)选择房地产价格时间序列的最佳延迟时间(τ)和嵌入维数(n)，那么房地产价格时间序列x1,x2,…,xN转化为训练样本为输入向量，ti=xi+n为输出向量，K=N-n≥L。

(2)根据(X1,t1)，(X2,t2)，…，(Xk,tk)计算初始输出权值：

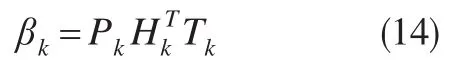
式中，C为岭回归系数；Ik为单位矩阵；

(3)将Xk+1=[xN-n+1,xN-n+2,…xN]T作为极限学习机的输入，计算神经元矩阵输入向量hk1，得到房地产价格样本xN+1的一步预测值：

(4)当采集到房地产价格样本xN+1的实际值后，首先根据式(7)对Pk进行选择性更新：

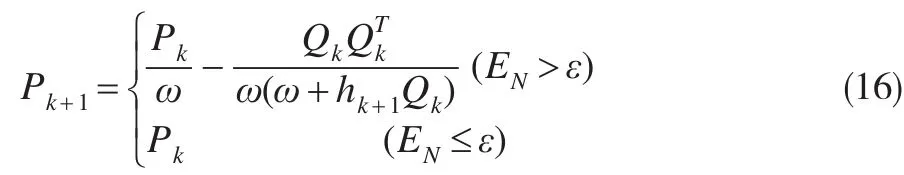
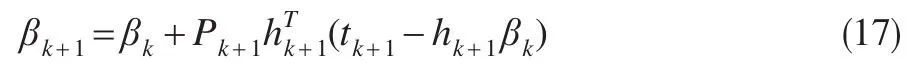
式中，tk+1=xN+1

(5)房地产价格训练集的样本数加1，并跳转到步骤(3)，直到所有训练样本训练完为止。

3 仿真实验

3.1 源数据

选取中国房屋销售价格指数月度数据进行实证分析，数据来源于中经网统计数据库1998年10月到2011年12月的房地产价格，共收集到158个数据点，具体如图1所示。

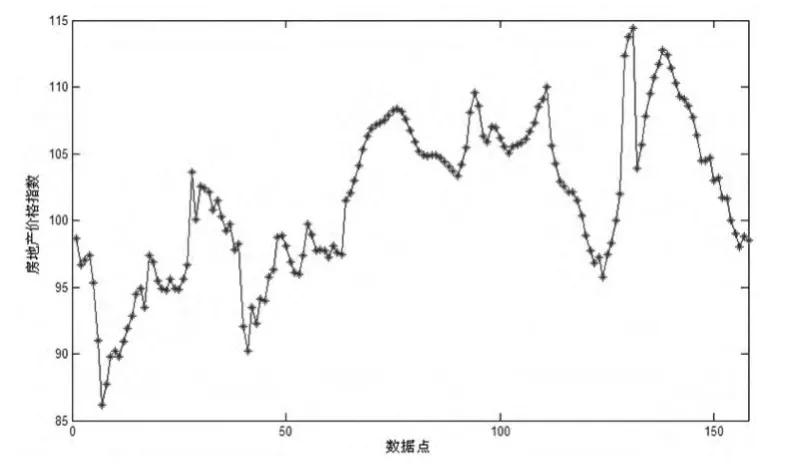
图1 收集的房地产价格数据

3.2 对比模型及评价标准

为了使RF-ELM的房地产价格预测结果具有可比性，选择OS-ELM、ELM作为对比模型。采用均方根误差(RMSE)和平均相对百分比误差(MPAE)作为模型的评价标准，分别定义如下：

3.3 学习样本的构造

3.3.1 选择时间延迟

首先采用采用互信息法进行时间延迟(τ)的计算，如图2所示。从图2可知，当τ=4时，互信息函数达到第一极小值，所以房地产价格时间序列的最佳时间延迟为τ=4。

图2 时间延迟(τ)的计算

3.3.2 嵌入维数确定

(1)根据互信息法求出τ=4，将嵌入维数的初值设为m=1。

(2)选择合适的临界距离r，根据式(20)计算Cn(r)，向量距离采用∞范数计算，即两个向量最大分量差作为向量距离。

式中，r表示临界距离的大小；M表示相点的个数；θ表示Heaviside单位函数。

(3)采用最小二乘法对logC(r)n～logr曲线中的直线段进行拟合，得到直线的斜率D，此时，D表示关联维数。

(4)为了获得最佳嵌入维数，将m值进行累加，返回步骤(2)。

依据以上步骤进行嵌入维数的求取，得到不同嵌入维数下的关联维数变化曲线如图5所示。从图5可知，当m=5时，关联维数已达到饱和状态，说明房地产价格时间序列的m=5。

图3 嵌入维数(m)的计算

采用最佳参数τ=4，m=5对房地产价格序列进行重构，然后将重构后的训练集输入RF-ELM模型进行训练，建立最优房地产价格预测模型，并对测试集进行预测。

3.4 结果与分析

3.4.1 房地产价格单步预测性能对比

RF-ELM参数为：遗忘因子ω=0.55，阈值ε=0.001，岭回归系数C=80，然后将训练集输入RF-FLM进行训练，最后对测试集进行单步预测，房地产价格预测结果和预测绝对误差如图3所示。从图3可知，房地产价格预测值与实际值之间十分接近，RMSE为1.84，MAPE%为1.06，由此可以看出利用RF-ELM模型进行房地产价格预测可以获得较高的预测精度。

图3 RF-ELM的单步预测性能

3.4.2 房地产价格多步预测性能对比

房地产价格预测的目标就是对房地产价格变化趋势进行把握，因此要求有一定提前预测时间，采用单步预测法对房地产价格投资决策实际应用价值不大，因此需要将单频预测扩展到多步预测。采用RF-ELM、OS-ELM和ELM对房地产价格进行建模与预测，2步、4步和6步预测结果的RMSE和MAPE%如表1所示。

表1 3种房地产价格预测模型的预测误差对比

对表1中3个模型在不同预测步长的性能进行分析，可以得到如下结论：

(1)传统极限学习机(ELM)在初始训练阶段完成后，网络输出权值不再发生改变，随着房地产价格预测步长逐渐增大，训练集与当前时刻间房地产价格预测点的距离越大，建立预测模型不能难以准确刻画当前时刻的房地产价格动态变化特性，房地产价格的预测精度比较低。

(2)相对于ELM，由于RF-ELM和OS-ELM不断利用新采集的房地产价格训练样本对预测模型进行在线更新，预测误差明显减小，此外，由于新采集的房地产价格训练样本与预测点间的距离最小，可以准确跟踪房地产价格动态变趋势，获得的房地产价格预测结果更加可靠。

(3)相对于OS-ELM，RF-ELM的预测误差更小，主要由于OS-ELM模型将距离房地产价格较远的房地产价格训练样本同等对待，然而，现实情况却是房地产与当前较近的时间点的房地产价格呈十分紧密的联系，而OS-ELM模型将所有的训练样本赋予同样的权重，难以准确反映房地产价格之间的时间相关性。而RF-ELM以遗忘旧训练样本的方式，对一些距离预测点较远，关联性较小的样本赋予较小的权值，将无用的样本数据点丢弃，突出了新的房地产价格训练样本对预测点影响，可以较好的捕捉真实房地产价格变化特性，从而可以获得了令人满意的预测效果。

3.3.3 其他房地产价格的预测

为了进一步测试本文模型的普适性，采用2000年1月到2012年8月长沙市房地产价格、2001年3月到2012年8月武汉市房地产价格、2002年5月2013年3月深圳市房地产价格、2003年2月到2012年11月湘潭市房地产价格进行仿真测试，得到相应预测结果，预测误差见表2。

表3 其它城市房地产价格预测精度

从表2可知，利用RF-ELM进行各地房地产价预测，均获得了较好的预测精度，长沙市房地产价格的RMSE、MAPE分别为6.73和4.00，其余三地的房地产价格预测值的MAPE均小于4.00，都具有较高的预测精度，结果表明，因此，RF-ELM是一种预测精度高的房地产价格预测模型。

4 结束语

为了提高房地产价格的预测精度，针对房地产价格训练样本选择问题，提出了一种基于合理遗忘历史样本的房地产价格预测模型。仿真结果表明，相对对比模型，RF-ELM提高了房地产价格的预测精度，加快了训练速度，可以更好的满足房地产价格在线预测要求。由于房地产价格是受政治、经济、供给、需求等多种因子的影响，本研究只房地产价格历史时间序列数据，没有考虑到这些因素的影响，综合考虑多种因子对房地产价格的影响，有待进一步研究。

[1]章晨,郑循刚,龚沁.基于ARMA模型的我国房地产价格预测分析[J].生产力研究2012,(2).

[2]柳冬,王雯珺,汪寿阳.我国房地产价格影响要素分析与趋势预测[J].经济与金融,201,22(5).

[3]杨励雅,邵春福.基于BP神经网络与马尔可夫链的城市轨道交通周边房地产价格的组合预测方法[J].吉林大学学报(工学版),2008,38(3).

[4]周亮,周正.基于时间序列的房地产价格指数预测方法探讨[J].哈尔滨商业大学学报(社会科学版),2008,(2).

[5]李万庆,张金水,孟文清.基于小波神经网络的房地产价格指数预测研究[J].河北工业大学学报(自然科学版)[J].2008,25(1).

[6]梁坤,聂会星,徐枞巍.基于支持向量机的北京市房地产价格指数预测[J].合肥工业大学学报,2011,34(4).

[7]钟昌宝.基于灰色-马尔柯夫模型预测房地产价格[J].统计与决策,2005,(1).

[8]胡晓龙,郜振华,马光红.基于Elman神经网络的房地产价格预测[J].统计与决策,2008,(7)．

[9]Callado A,Keu R J,Sadok D,et a1.Better Network Traffic Identification Through The Independent Combination of Techniques[J].Journal of Network and Computer Applications,2012,33(4).

[10]高光勇,蒋国平.采用优化极限学习机的多变量混沌时间序列预测[J].物理学报,2012,61(4).

[11]张弦,王宏力.基于贯序正则极端学习机的时间序列预测及应用[J].航空学报,2011,32(7).